Наибольшее и наименьшее значение функции

1.

2. Промежутки возрастания и убывания функции

3. Точки экстремума

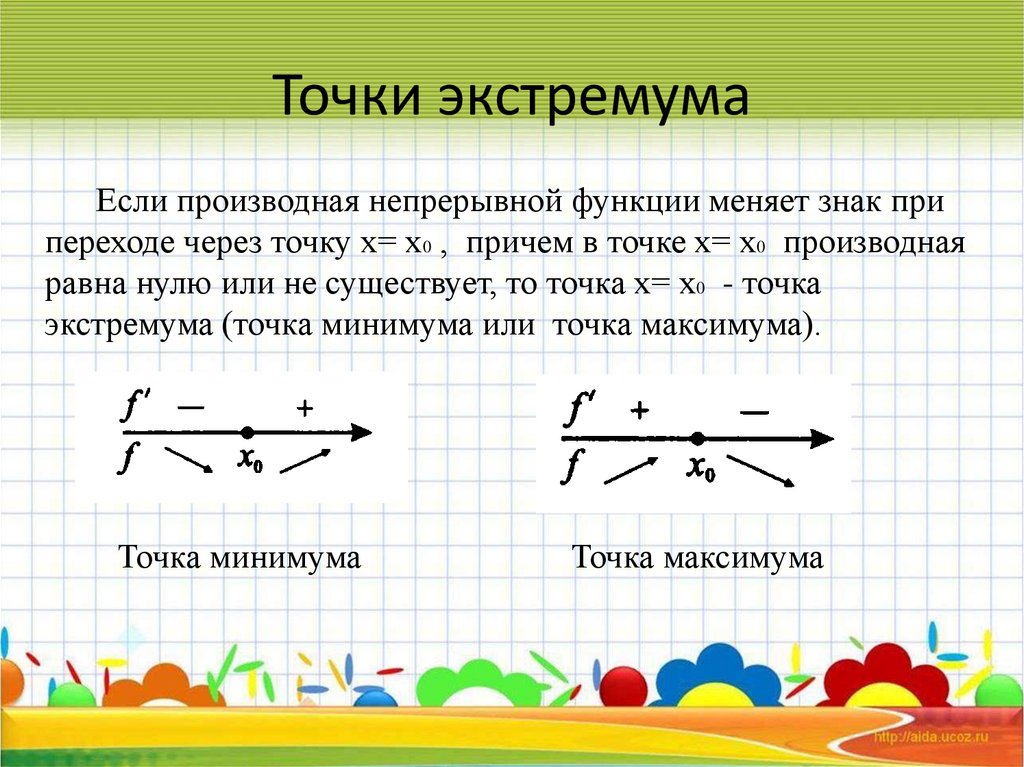
Если производная непрерывной функции меняет знак при
переходе через точку х= х0 , причем в точке х= х0 производная
равна нулю или не существует, то точка х= х0 - точка
экстремума (точка минимума или точка максимума).
Точка минимума
Точка максимума

4. График производной

По графику производной можно определить:

5. По графику функции у=f(x) найдите:

1.Область определения функции.
[-3;6]
2. Абсциссы точек в которых f`(x)=0
0;3,5
3. Наибольшее значение функции.
(Унаиб.).
Унаиб=3
4. Наименьшее значение функции
(Унаим.).
Унаим.=-2

6. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]

7. Первый способ

8. Второй способ

9. Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]

1. Найти производную f`(x)
2. Найти стационарные и критические точки
функции, лежащие внутри отрезка [a;b]
3. Вычислить значения функции у=f(x) в точках,
отобранных на втором шаге, и в точках a и b
выбрать среди этих значений наименьшее(это
будет Унаим.) и наибольшее (это будет Унаиб.).

10.

Пример: Найти наибольшее и наименьшее значение функции f(х)=2х3-3х2+2 на отрезке [2;3]
Решение:
1) f(-2)=2∙(-2)3-3∙(-2)2+2=-16-12+2=-26
f(3)=2∙33-3∙32+2=54-27+2=29
2) f′(х) =(2х3-3х2+2)′= (2х3)′-(3х2)′+(2)′=2∙3х2-3∙2х+0=6х2-6х
3) f′(х) =0 6х2-6х =0
х(6х -6)=0
х=0 или 6х-6=0
6
6х=6 , х=
6
х=1
1) Получили стационарные точки х1=0, х2=1,
по заданию имеем отрезок [-2;3], х1 и х2 входят в заданный отрезок, значит обе
стационарные точки нам подходят.
5) f(0)=2∙03-3∙02+2=0-0+2=2
f(1)=2∙13-3∙12+2=2-3+2=1
6) Имеем:
f(-2)= -26
f(3)= 29
f(0)=2
f(1)= 1
Выбираем самое большое и самое маленькое значение:
Наибольшее значение: f(3)= 29 , наименьшее значение: f(-2)= -26
Ответ: наибольшее значение: f(3)= 29 ,
наименьшее значение: f(-2)= -26

11.

12.

Ответ: - 1.