Похожие презентации:
Потенциал электростатического поля
1. Потенциал электростатического поля
2.
Eq+Q
2
1
dA F dr F dr cos( F , dr ) q E dr
kQ
q 2 dr
r
r
2
kQ
1
1
A q 2 dr k
kqQ( )
r
r
r2 r1
r1
3.
Работа поля поперемещению
заряда равна убыли
потенциальной
энергии
A1 2 (U 2 U1 )
U k
Const
r
r , U 0, Const 0
4. Потенциал
Uq
Не зависит от q и
является
энергетической
характеристикой
поля, называемой
потенциалом
5.
Потенциал поля точечного заряда QQ
k
r
Потенциал – скалярная величина
6. Потенциал
Потенциал электростатического поля –это потенциальная энергия единичного
положительного заряда в заданной
точке поля
Потенциал
электростатического поля –
это работа по перемещению единичного
положительного заряда из заданной
точки в бесконечность
7. Разность потенциалов
Разность потенциалов – это работа поперемещению единичного положительного
заряда из одной точки поля в другую
A1 2 (U 2 U1 ) U1 U 2 q( 1 2 )
2
A1 2
1
2
F dr q E dr
1
2
E
d
r
1
2
1
8. Принцип суперпозиции для потенциала
Потенциал поля,создаваемого
системой зарядов,
равен
алгебраической
сумме потенциалов,
создаваемых
каждым из зарядов
по отдельности
N
i
i 1
N
Qi
4 0 i 1 ri
1
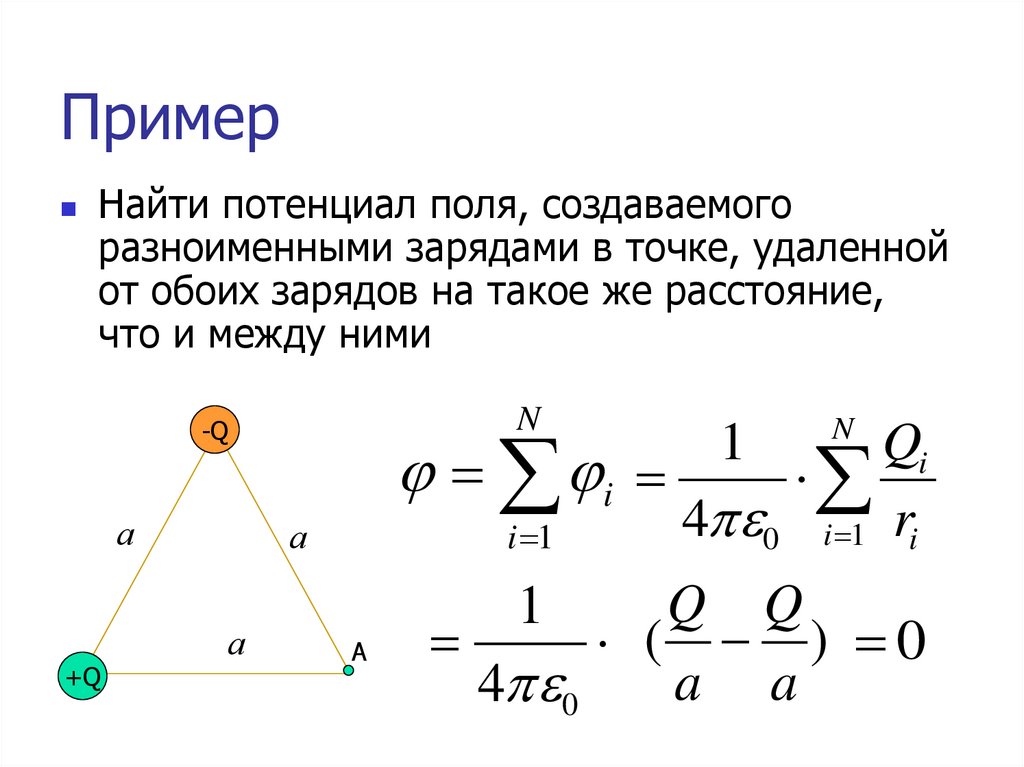
9. Пример
Найти потенциал поля, создаваемогоразноименными зарядами в точке, удаленной
от обоих зарядов на такое же расстояние,
что и между ними
N
-Q
а
+Q
а
а
N
Qi
i
4 0 i 1 ri
i 1
Q Q
( ) 0
a a
4 0
1
А
1
10. Эквипотенциальные поверхности – графический способ изображения электростатического поля
Эквипотенциальныеповерхности – это
поверхности во всех
точках которых
потенциал имеет одно
и тоже значение
const
11. Эквипотенциальные поверхности
Эквипотенциальные поверхностипроводят так, что разность потенциалов
между соседними поверхностями
одинакова
Густота эквипотенциальных поверхностей
характеризует напряженность
электростатического поля
Линии
напряженности всегда
перпендикулярны эквипотенциальным
поверхностям
12. Пример
Qk
r
+q
E
φ3
φ2
φ1
1 2 2 3
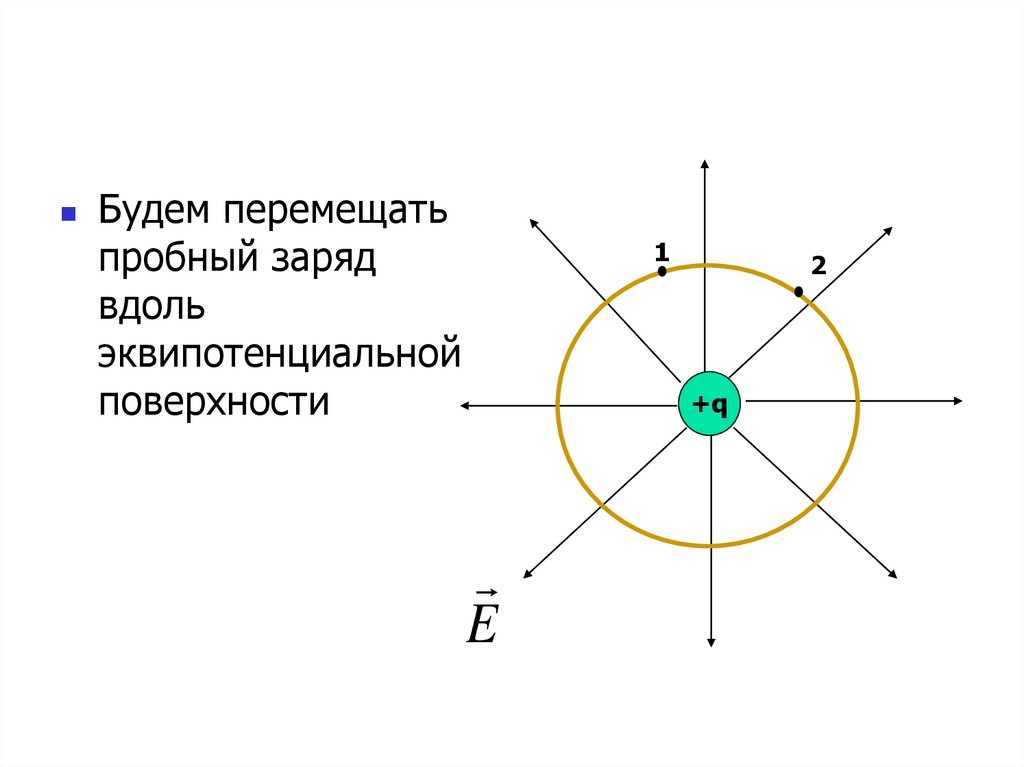
13.
Будем перемещатьпробный заряд
вдоль
эквипотенциальной
поверхности
1
2
+q
E
14.
2E dr 1 2
1
2
1
E dr cos E , dr 1 2
1 2 0
E 0 , dr 0
cos E , dr 0
E dr
15. НАПРЯЖЕННОСТЬ КАК ГРАДИЕНТ ПОТЕНЦИАЛА
16.
i , j, kЕдиничные орты осей
z
k
x
i
j
y
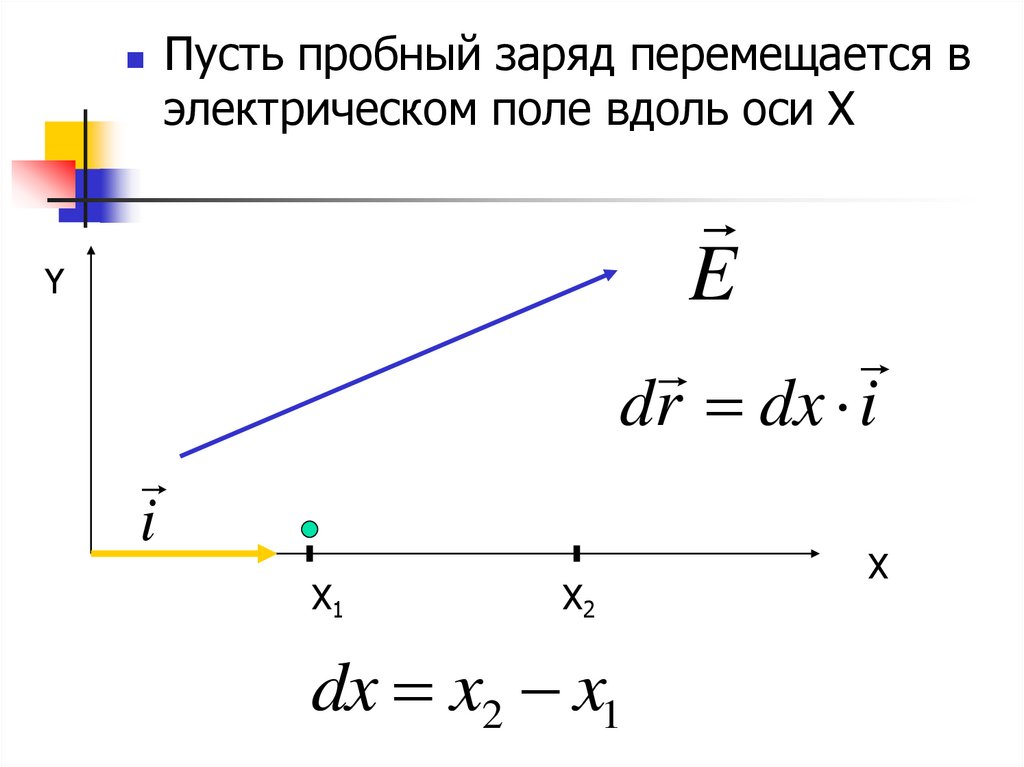
17.
Пусть пробный заряд перемещается вэлектрическом поле вдоль оси Х
E
Y
dr dx i
i
Х1
Х2
dx x2 x1
Х
18.
2E dr 1 2 d
2
1
1
E dr Ex dx E y dy Ez dz
Ex dx
2
2
1
1
d
E
dx
x
d
Ex
dx
19.
Аналогично, перемещая заряд вдольоси Y и оси Z
d
Ey
dy
d
Ez
dz
В общем случае
d
d
d
E
i
j
k
dy
dz
dx
20.
E gradГрадиент – это вектор
grad
i
j
k
x
y
z
Знак (-) означает , что напряженность
направлена в сторону убывания
потенциала
21.
EE
E
+q
grad
E
22. ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА НАПРЯЖЕННОСТИ
1 1A kqQ( )
r2 r1
23.
Работа не зависит от траекторииперемещения заряда, определяется
только положениями начальной и
конечной точек
Электростатическое поля является
потенциальным
При перемещении по замкнутой
траектории работа равна 0
24.
dA0
L
q
(
E
d
r
)
0
dr dl
L
(
E
d
)
L
Циркуляция вектора
напряженности
25. Циркуляция в любом электрическом поле равна 0
Циркуляция E в любомэлектрическом поле равна 0
- теорема о циркуляции
(
E
d
)
0
L
26. Объемное распределение заряда
Объемная плотность заряда( x, y , z )
dq ( x, y, z )dV
( x, y, z )dxdydz
q ( x, y, z )dxdydz
V
27. Поверхностное распределение заряда (плоскость)
Поверхностная плотность заряда( x, y )
dq ( x, y )dS
( x, y )dxdy
q ( x, y )dxdy
S
28. Линейное распределение заряда (линия)
Линейная плотность заряда(x )
dq ( x)dx
q ( x)dx
29.
QE k 3 r
r
( x, y, z )r dV
E
3
r
( x, y )r dS
E
3
r
S
( x)r dx
E
3
r
V
30. ПРИМЕР
Напряженность и потенциалэлектрического поля в центре
однородно заряженного кольца
(заряд +Q, радиус кольца R)
31.
Разбиваем кольцо на элементарныезаряды
dq
dE
dE
dq
E dE
E 0
32.
dkdq
d
R
kdq
k
k
dq Q
R
R
R
33. НАПРЯЖЕННОСТЬ ПОЛЯ НА ОСИ ТОНКОГО КОЛЬЦА
dEНАПРЯЖЕННОСТЬ ПОЛЯ НА
ОСИ ТОНКОГО КОЛЬЦА
E
dE
А
X
dE x
dE x
z
dq
R
dEx 0
34.
E dE ydE y dE cos
dE y
R
z
dE
cos
z
R z
2
kdq
dE 2
2
R z
2
35.
Ez
R z
2
2
k z Q
R
2
z
2
2
3
kdq
2
2
R z
36.
Найдем потенциалE grad
i
j
k
y
z
x
k
z
37.
Edzk z Q
R
2
z R u
2
2
du d z R 2zdz
2
kQ
2
z
2
3
1
2
3
kQ
u
du
3
3
2 u 2
2
2 1
1
kQ
kQ u 2
1
2
2
R z
2
2
dz
2
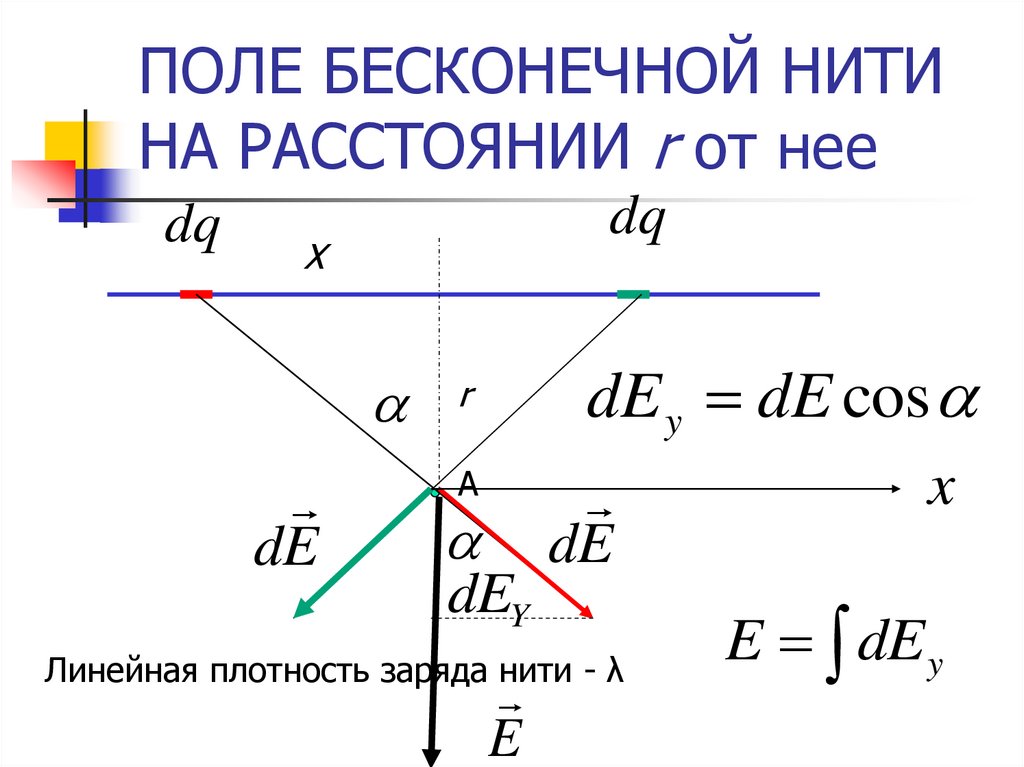
38. ПОЛЕ БЕСКОНЕЧНОЙ НИТИ НА РАССТОЯНИИ r от нее
dqdq
X
dE
dE y dE cos
r
A
dEY
dE
Линейная плотность заряда нити - λ
E
x
E dE y
39.
cosr
r x
2
2
kdq
dq
dx
dE 2
2
r x
k dx
r
E
2 2 r 2 x2
r x
r
r
2
x
2
2
3
k dx
40.
2k r0
dx
r
2
x
2k
E
r
2
3
2
41.
Потенциал поля бесконечной нитиE grad
Для полей с радиальной
симметрией
Er
r
2k
dr
Edr
r
2k ln r Const
































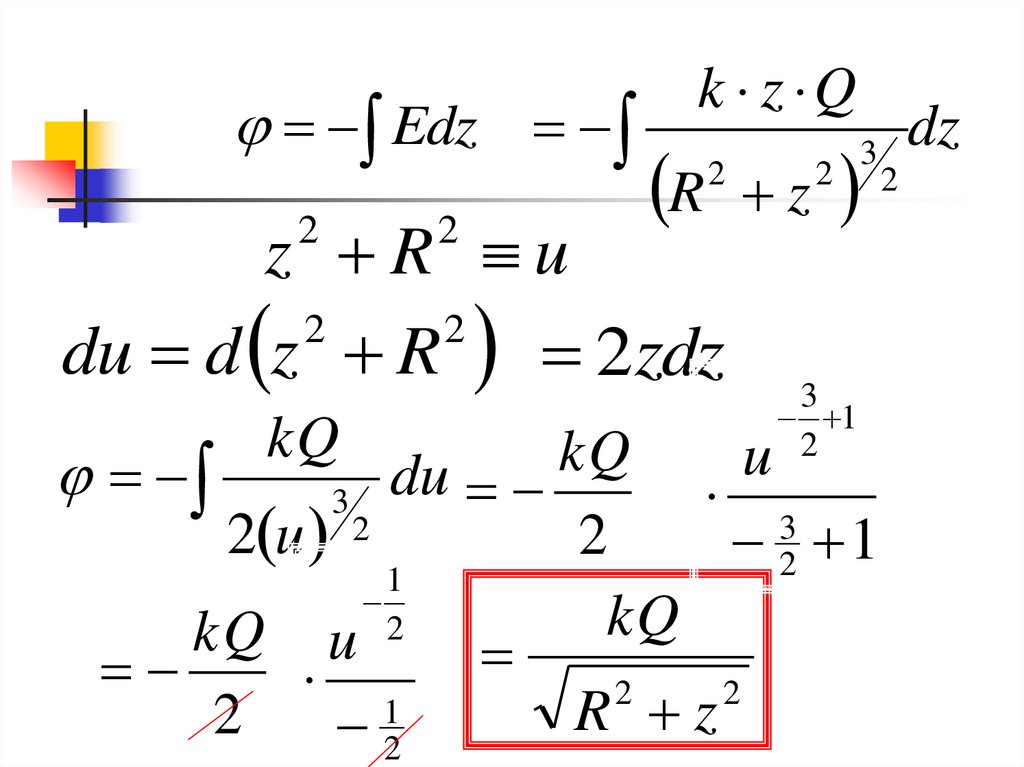



 Физика
Физика








