Похожие презентации:
Энтропия. Термодинамическая энтропия
1. Энтропия
2.
• Введено в 1865 году Клаузиусом• приведенное количество теплоты,
сообщаемое телу на бесконечно малом
участке процесса, когда температура
постоянна
Q
T
• Для любого обратимого процесса
Q
T
0
3.
• Приведенная теплота – функция состояния,для которой не важен путь, по которому
идет процесс
• Термодинамическая энтропия – S
Q
Дж
S
S
К
T
• При переходе из состояния 1 в состояние 2
изменение энтропии
2
S1 2 S2 S1
1
Q
T
4.
• Энтропия определяется c точностью донекоторой постоянной
• Физический смысл имеет разность
энтропий
5.
2S
1
dU
m
Q
T
dU A
T
1
2
cV dT
A pdV
pV
1 m
A RT dV
V
m
RT
1 m
p RT
V
6.
m2
S
1
m
2
m
1
cV dT RT dV
V
T
2
dT
m
dV
cV
R
1 T
1 V
m
T2 m
V2
cV ln
R ln
S
T1
V1
7.
V constT const
Q 0
m
T2
S cV ln
T1
m
V
S R ln 2
V1
S 0
Адиабатический процесс
8.
• Энтропия обладает свойствомаддитивности: энтропия нескольких газов
равна сумме энтропий каждого газа в
отдельности
9.
• Рассмотрим теплоизолированный сосуд,разделенный перегородкой на 2 части.
m1
V1
• 1cV 1
T1
1
• 2-
V2
m2
2
cV 2
T2
10.
Перегородку убирают
Газы перемешиваются
Найдем температуру после перемешивания
(равновесного состояния)
m1
1
cV 1 T T1
m1
T
1
cV 1T1
m1
1
cV 1
m2
2
m2
2
m2
2
cV 1 T2 T
cV 2T2
cV 2
11.
• Если• то
m1
1
m2
2
T1 T2
T
2
cV 1 cV 2
12.
• Для 1 газа изменение энтропииm1
T
dT
S1 cV 1
1 T T
1
m1
V
dV
R
1 V V
1
• Для 2 газа изменение энтропии
T
V
dT m2 R dV
S2
cV 2
2 V V
2
T
T
2
m2
2
13.
m1T
V
S cV 1 ln R ln
1
T1
V1
m2
T
V
cV 2 ln R ln
2
T2
V2
14.
• Еслиm1
1
m2
2
1
cV 1 cV 2
T1 T2
• то
V1 V2
S cV 1 ln1 R ln 2 cV 2 ln1 R ln 2
2R ln2
• Энтропия увеличилась!
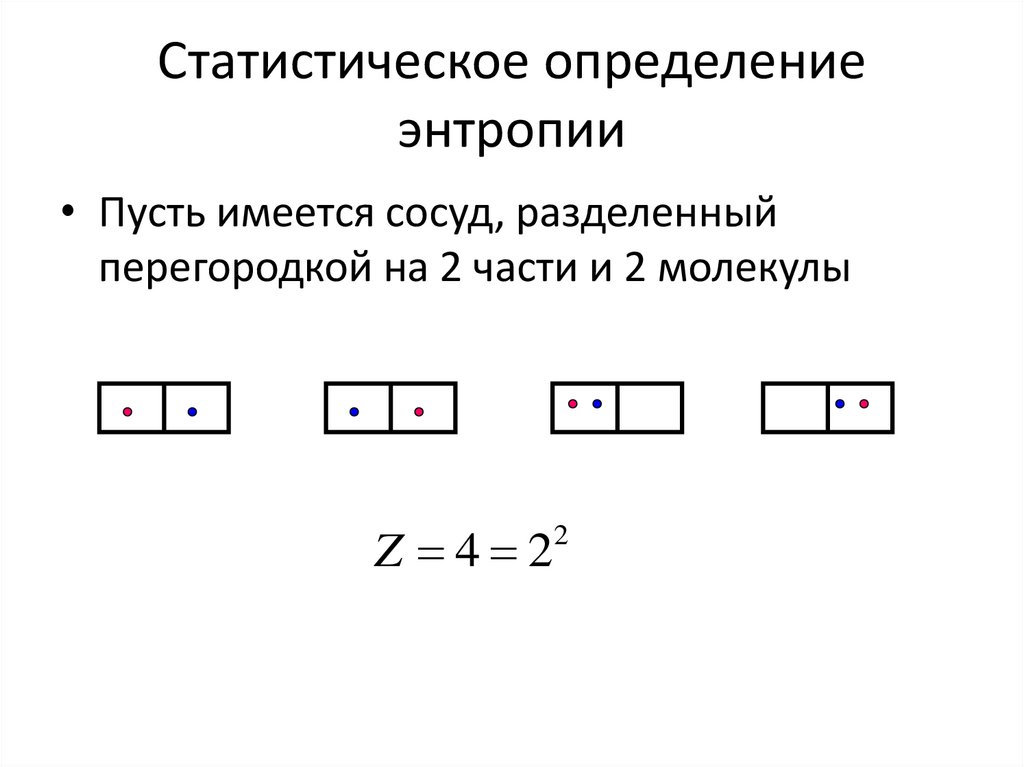
15. Статистическое определение энтропии
• Пусть имеется сосуд, разделенныйперегородкой на 2 части и 2 молекулы
Z 4 2
2
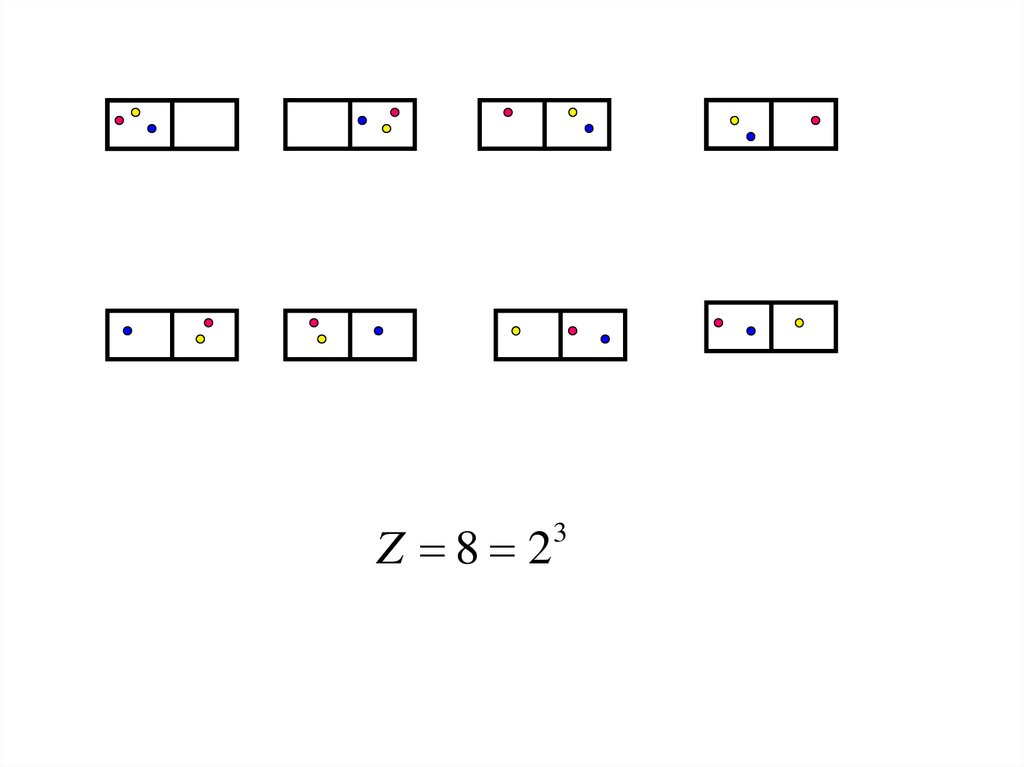
16.
Z 8 2317.
• Если молекул N, то их можно распределитьмежду двумя половинками
Z 2
способами
N
18.
• Термодинамической вероятностью (W) назчисло способов, с помощью которых может
быть реализовано данное макросостояние
системы.
• Пример: Найти термодинамическую
вероятность когда все три молекулы
находятся в одной половине сосуда?
W=2
W 1
19.
• ЭнтропияS k ln W
• Больцман
• Мера вероятности данного состояния газа
• Указывает направление протекания
самопроизвольных процессов
20. Закон возрастания энтропии (второе начало термодинамики)
• Первое начало термодинамики – законсохранения энергии
• Не указывает направление протекания
процессов
• Из определения энтропии следует, что при
обратимых процессах энтропия не меняется
S 0
21.
• В замкнутых системах при необратимыхпроцессах энтропия всегда возрастает
• Процесс идет от менее вероятного к более
вероятному
S 0
• Это справедливо для систем, состоящих из
большого числа частиц
22. Закон возрастания энтропии
• Второе начало термодинамики указываетнаправление протекания обратимых и
необратимых процессов
• Неравенство Клаузиуса
S 0
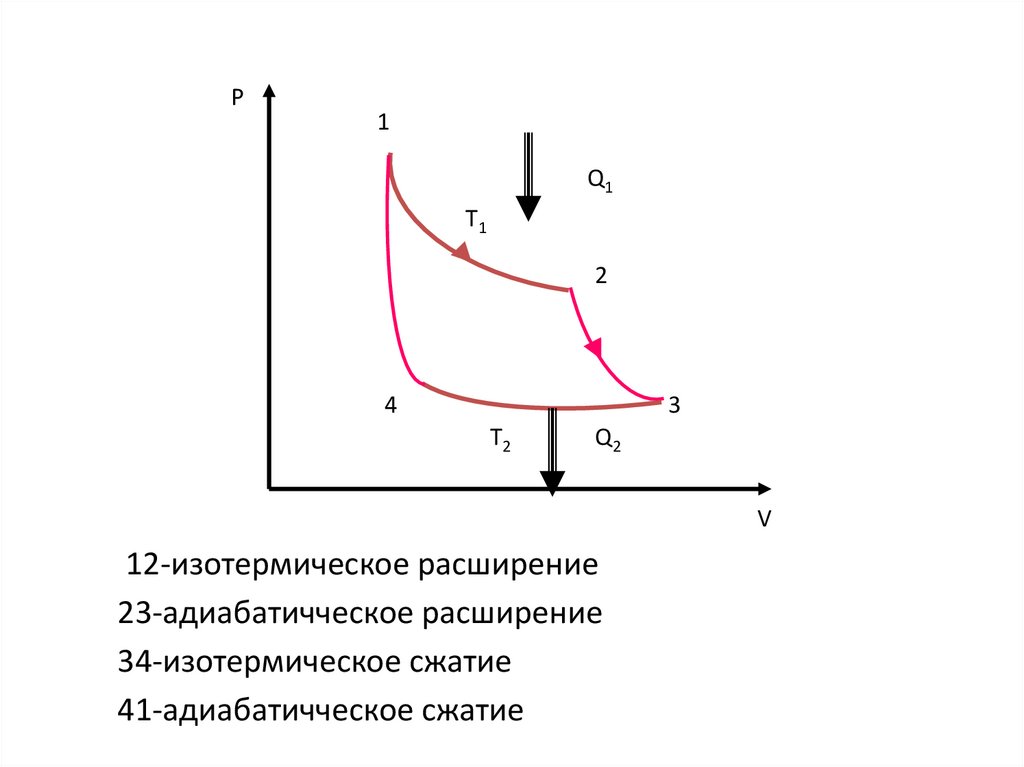
23. ЦИКЛ КАРНО
• Наиболее экономичный цикл тепловогодвигателя.
• Состоит из 2 изотерм и двух адиабат
24.
P1
Q1
T1
2
4
3
T2
Q2
V
12-изотермическое расширение
23-адиабатичческое расширение
34-изотермическое сжатие
41-адиабатичческое сжатие
25.
1 2T const
2 3
U12 0
m
V2
Q1 A12 RT1 ln
V1
Q 23 0
A23 U 23
m
m
cV T
cV (T2 T1 )
26.
3 4U34 0
m
V4
Q 2 A34 RT2 ln
V3
T const
4 1
Q41 0
A41 U 41
m
cV (T2 T1 )
m
cV T
A23
27.
Q1 Q2Q1
m
V2
Q1 RT1 ln
V1
m
V4
Q 2 RT2 ln
V3
28.
2 3TV -1 const
T1V2
4 1
-1
T2 V4
-1
T2 V3
-1
-1
V3
V2
-1
-1
V1
V4
-1
-1
T1V1
V2 V3
V1 V4
29.
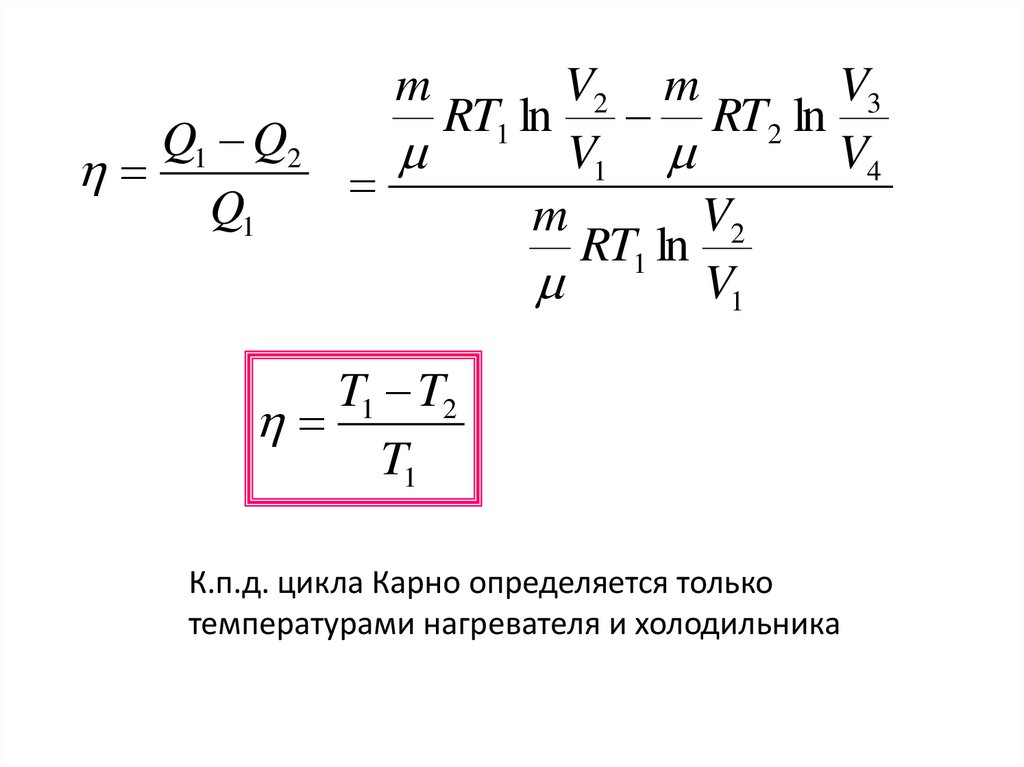
Q1 Q2Q1
V3
V2 m
RT1 ln RT2 ln
V1
V4
m
V2
RT1 ln
V1
m
T1 T2
T1
К.п.д. цикла Карно определяется только
температурами нагревателя и холодильника
30.
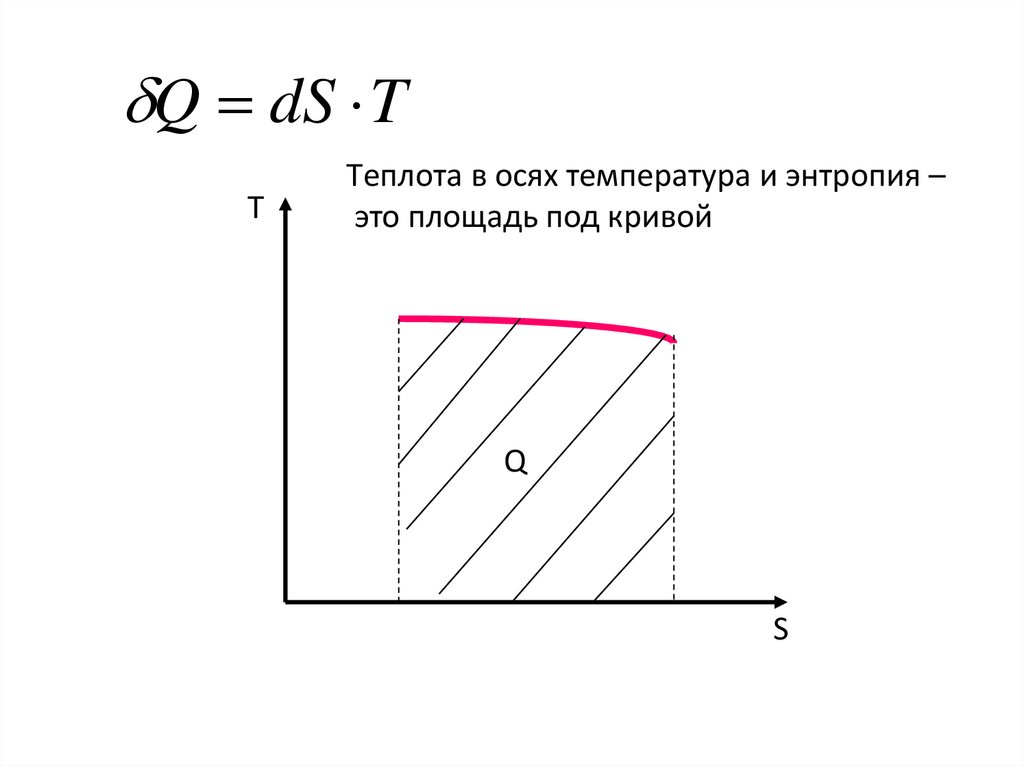
Q dS TТ
Tеплота в осях температура и энтропия –
это площадь под кривой
Q
S
31.
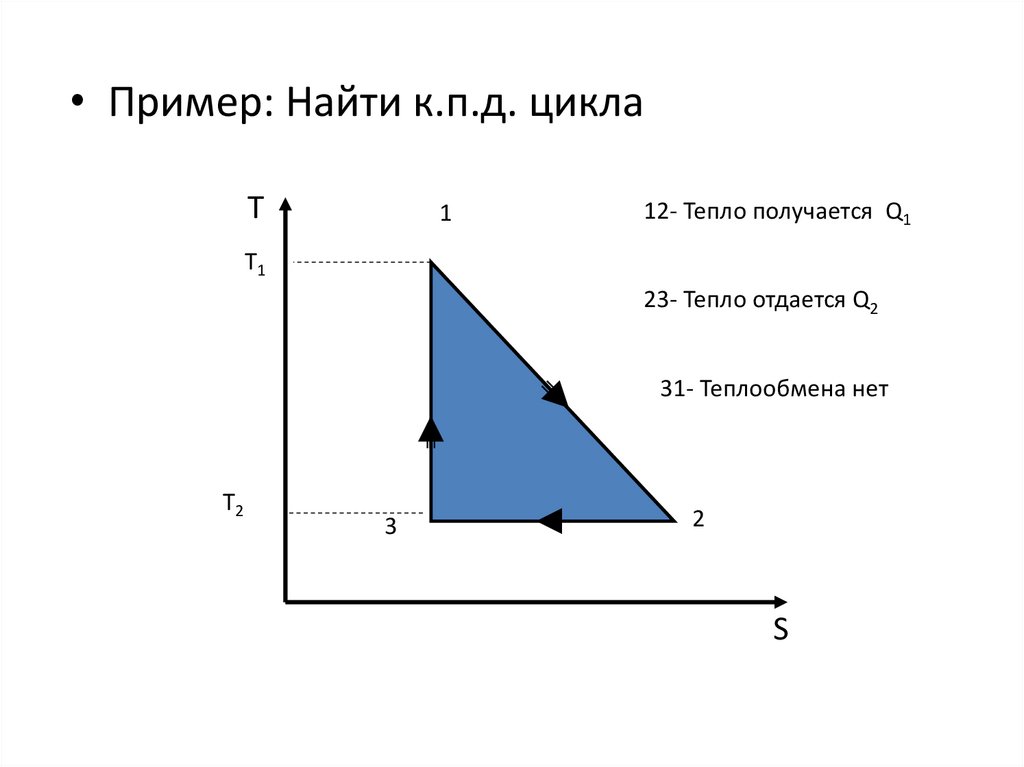
• Пример: Найти к.п.д. циклаТ
1
12- Тепло получается Q1
T1
23- Тепло отдается Q2
31- Теплообмена нет
T2
3
2
S
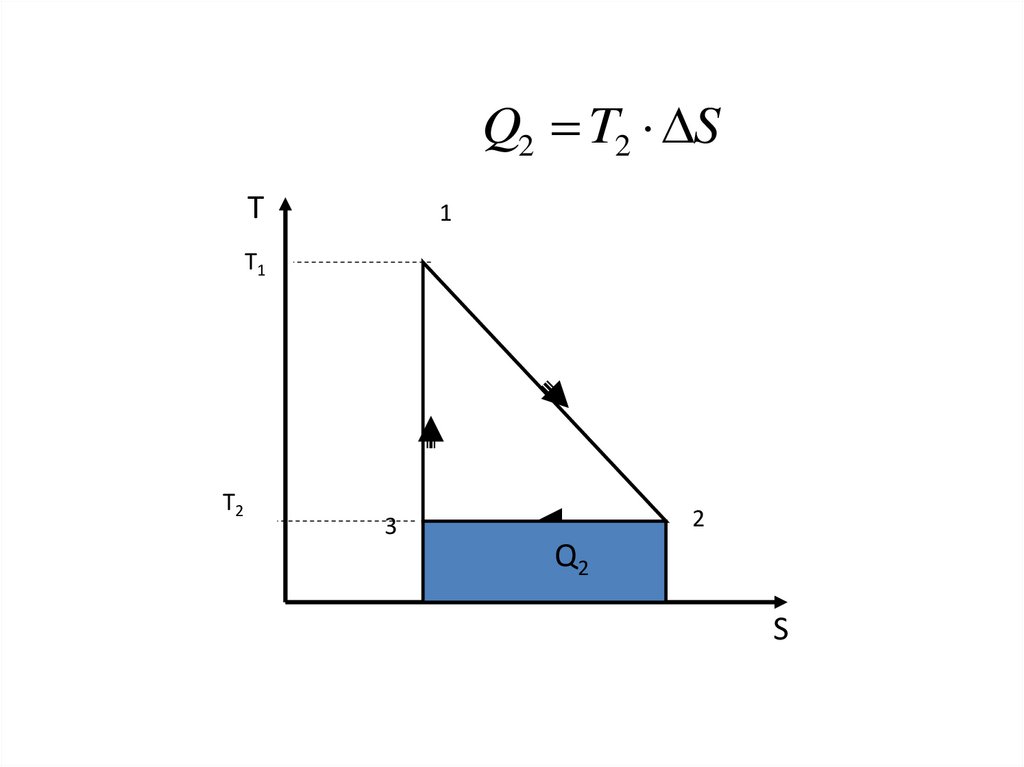
32.
ТT1
T2
1
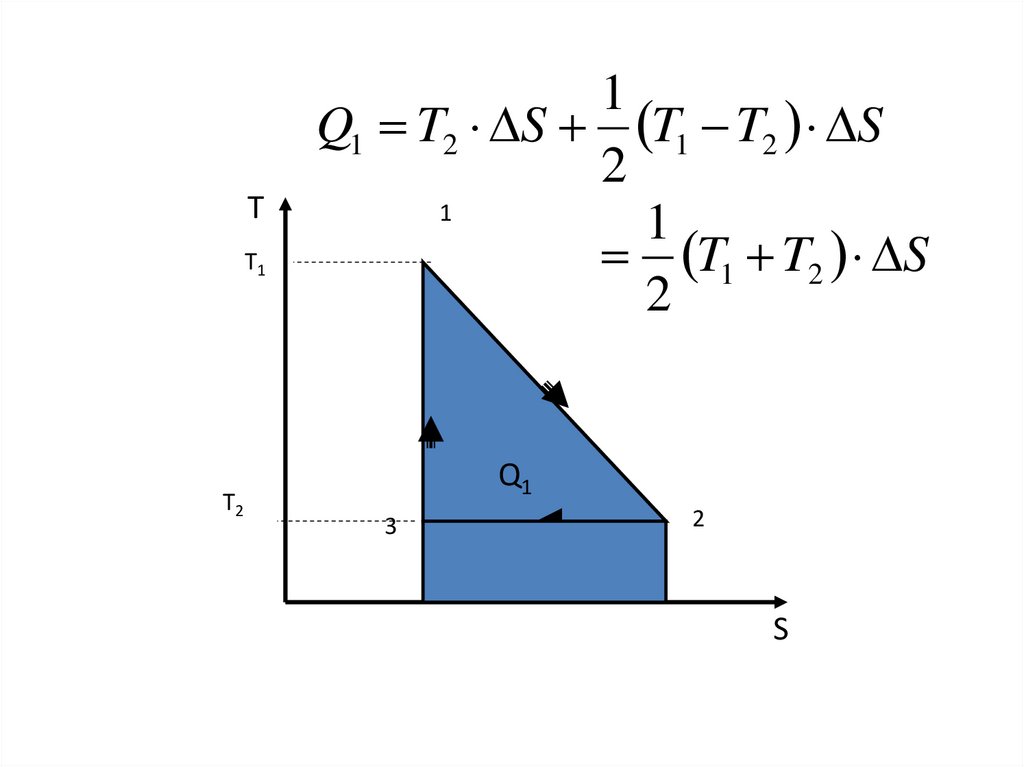
Q1 T2 S T1 T2 S
2
1
1
T1 T2 S
2
Q1
3
2
S
33.
Q2 T2 SТ
1
T1
T2
2
3
Q2
S
34.
Q21
Q1
1
T1 T2 S
2
1
T2 S
1 T2 T1
2
T2
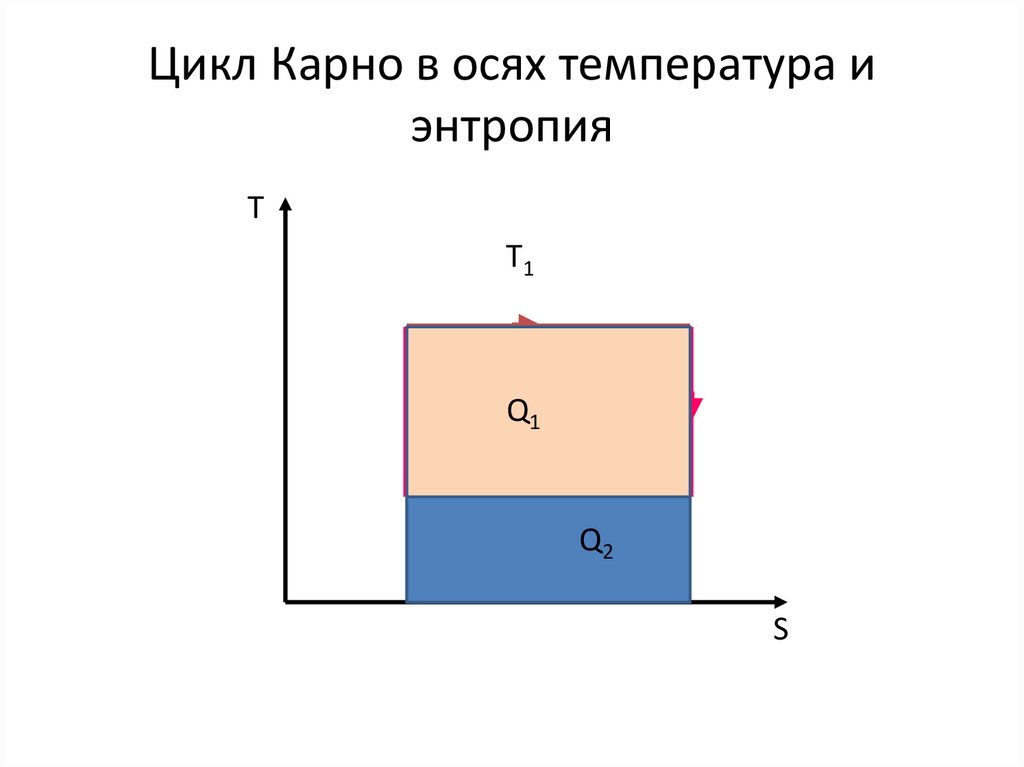
35. Цикл Карно в осях температура и энтропия
ТT1
Q1
T2 Q
2
S
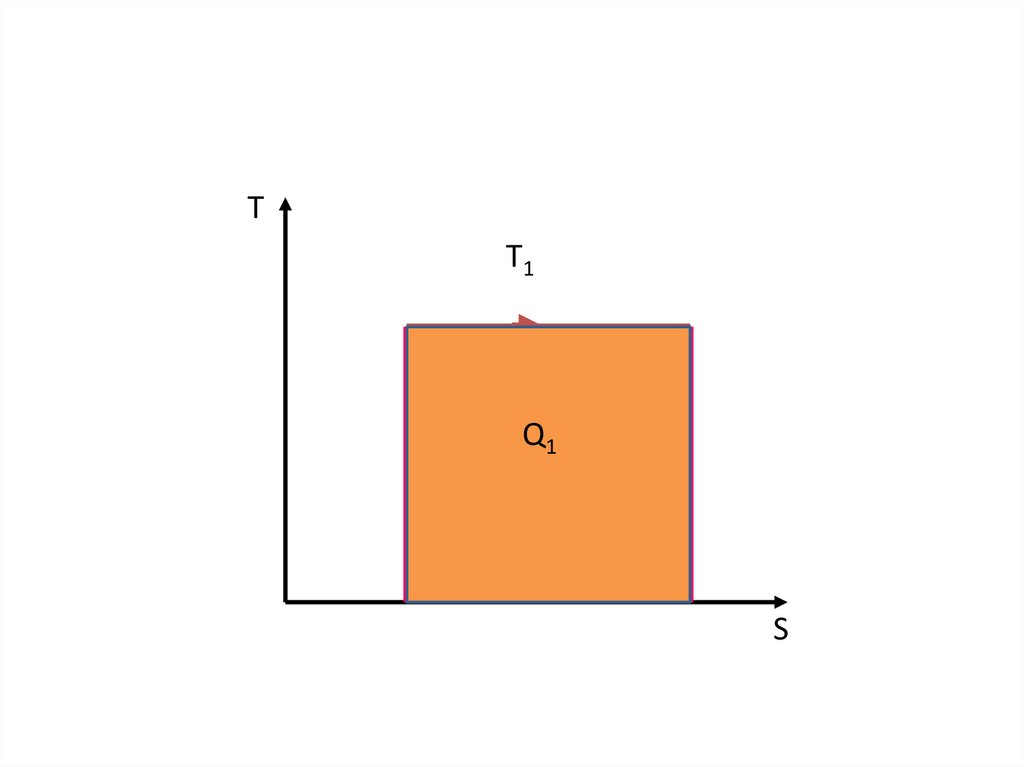
36.
ТT1
Q1
S
37.
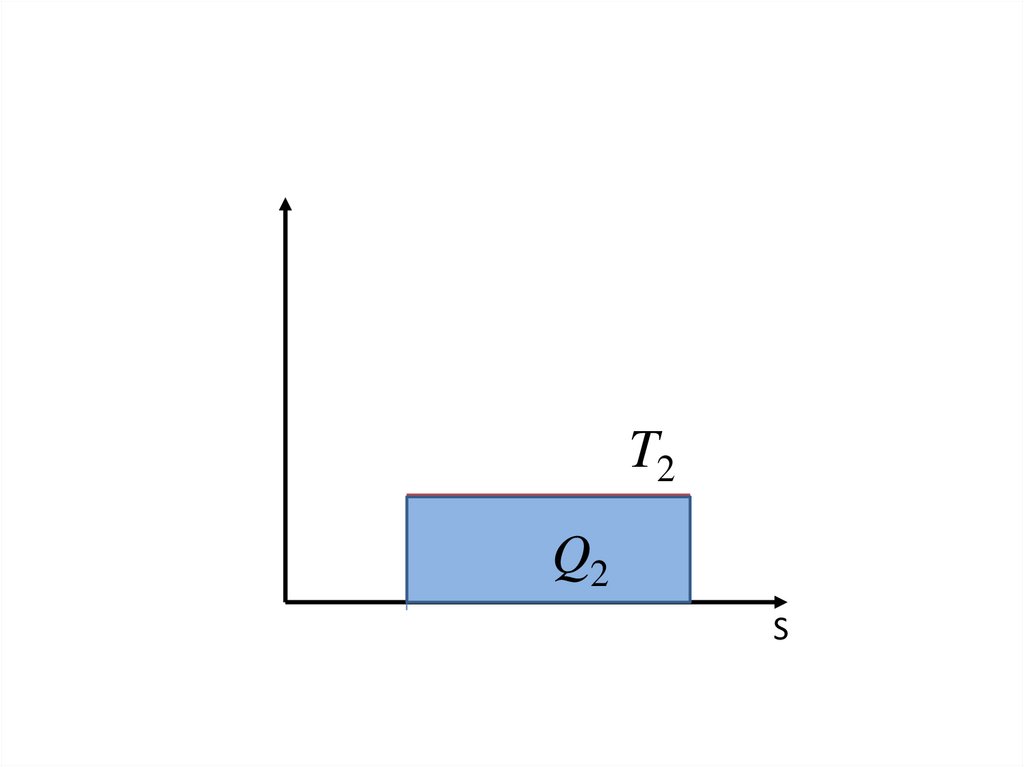
T2T2
Q2
S
38.
Q21
Q1
Q1 T1 S
Q2 T2 S
T
1 2
T1




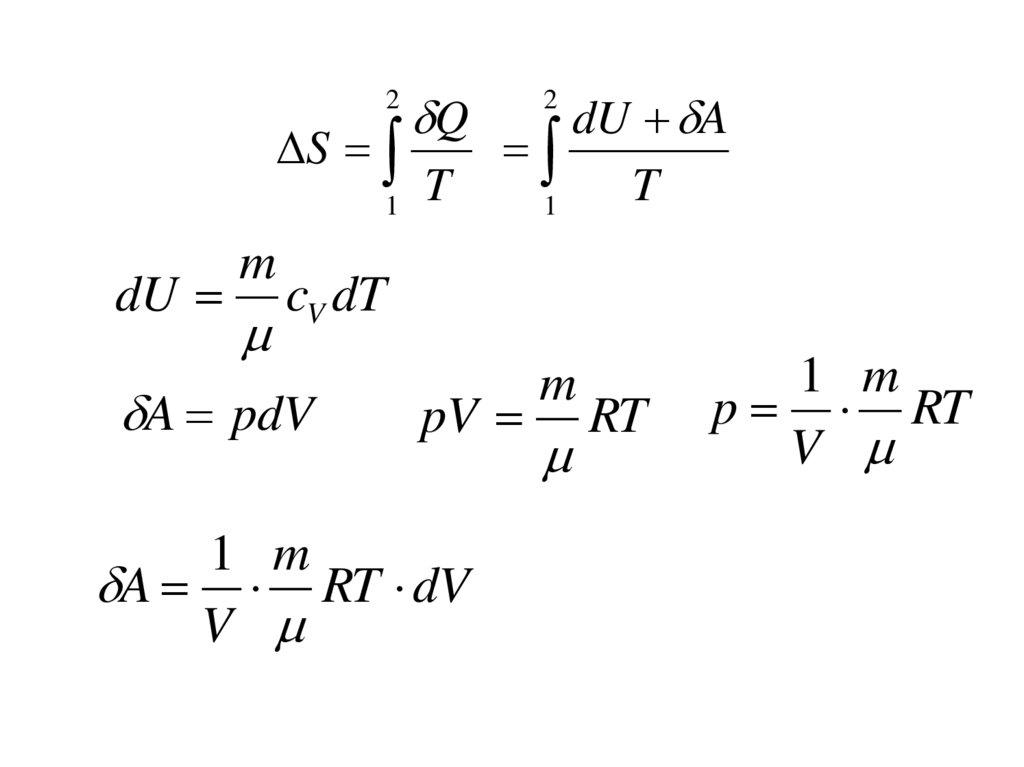
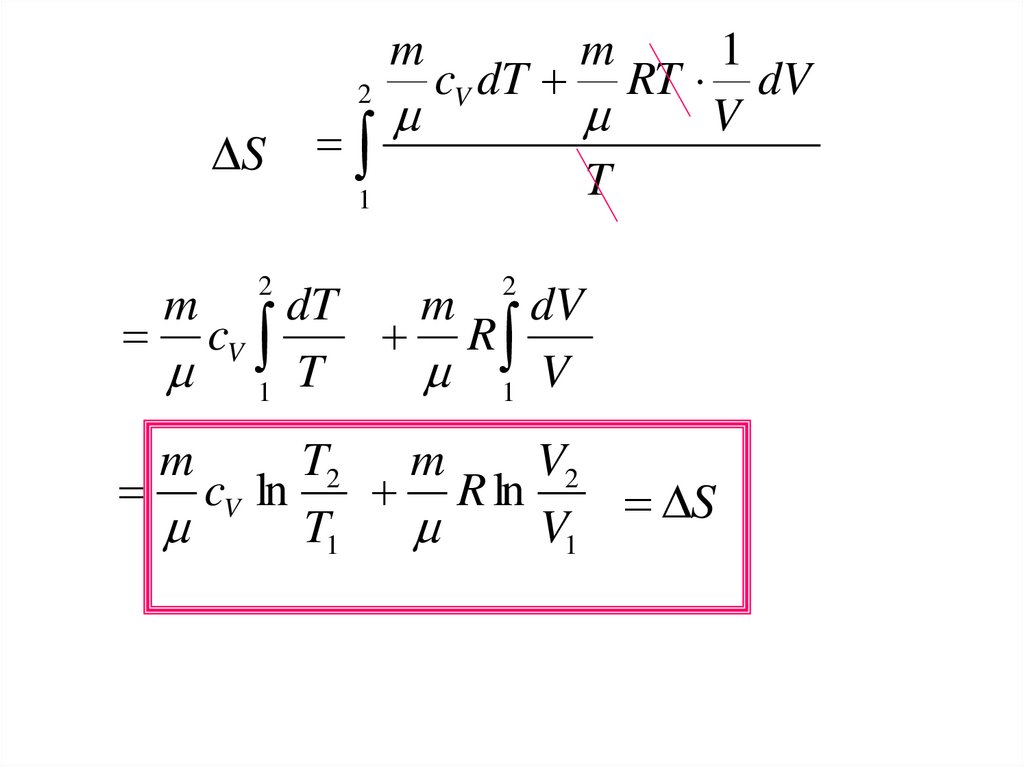




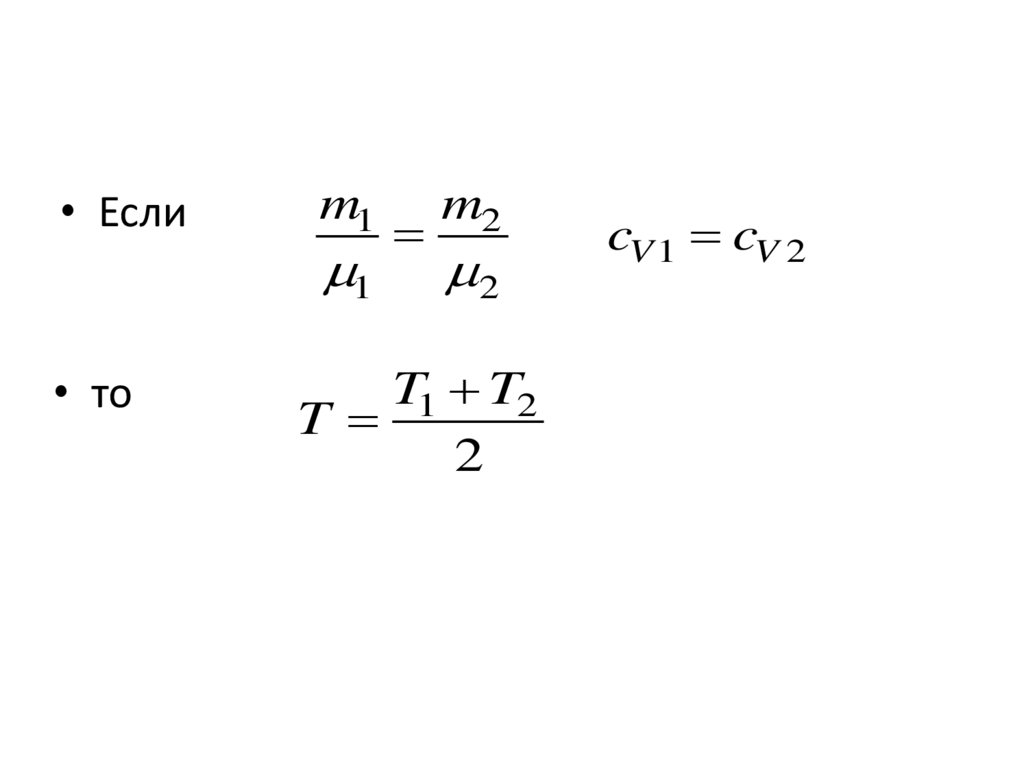
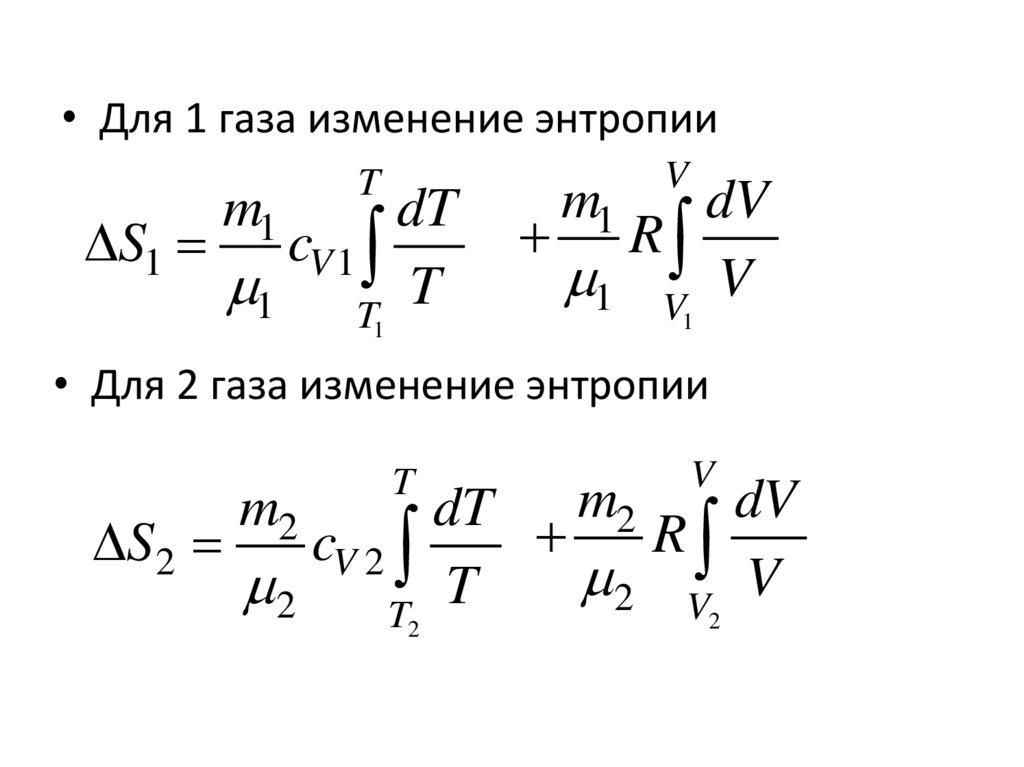
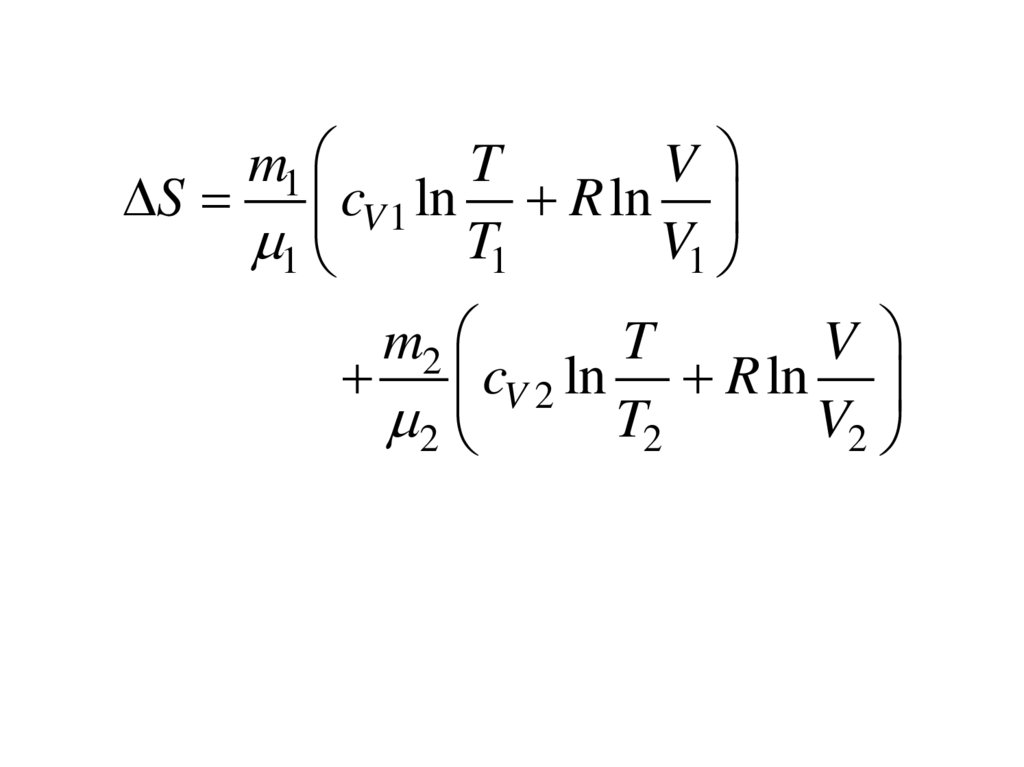
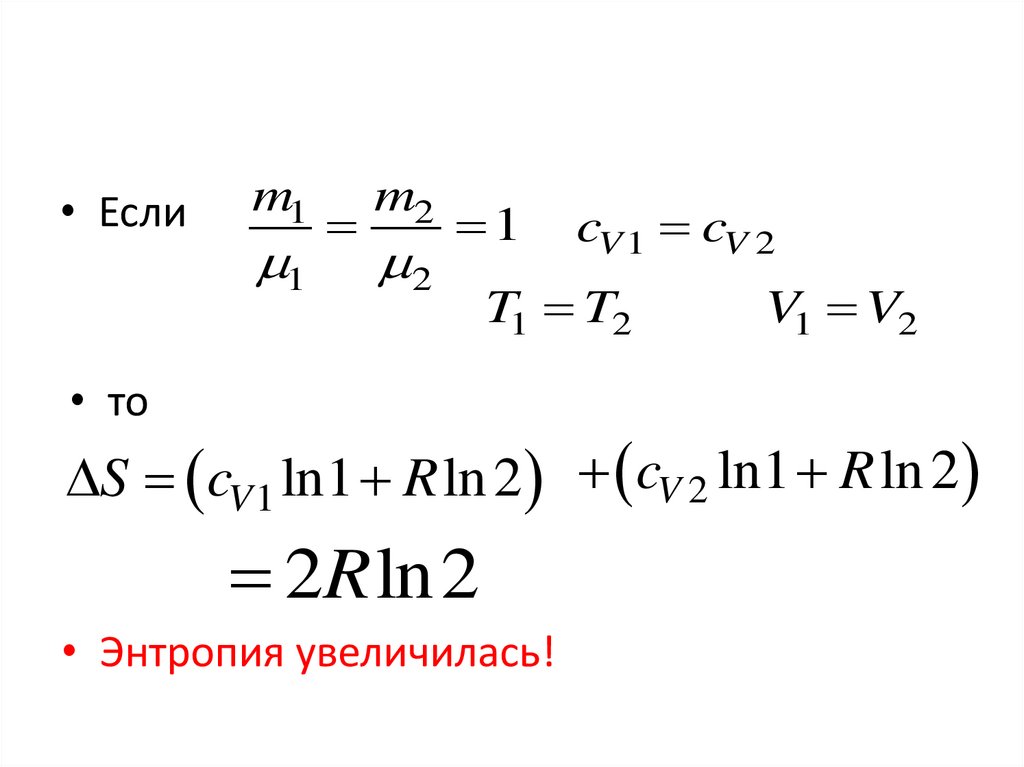







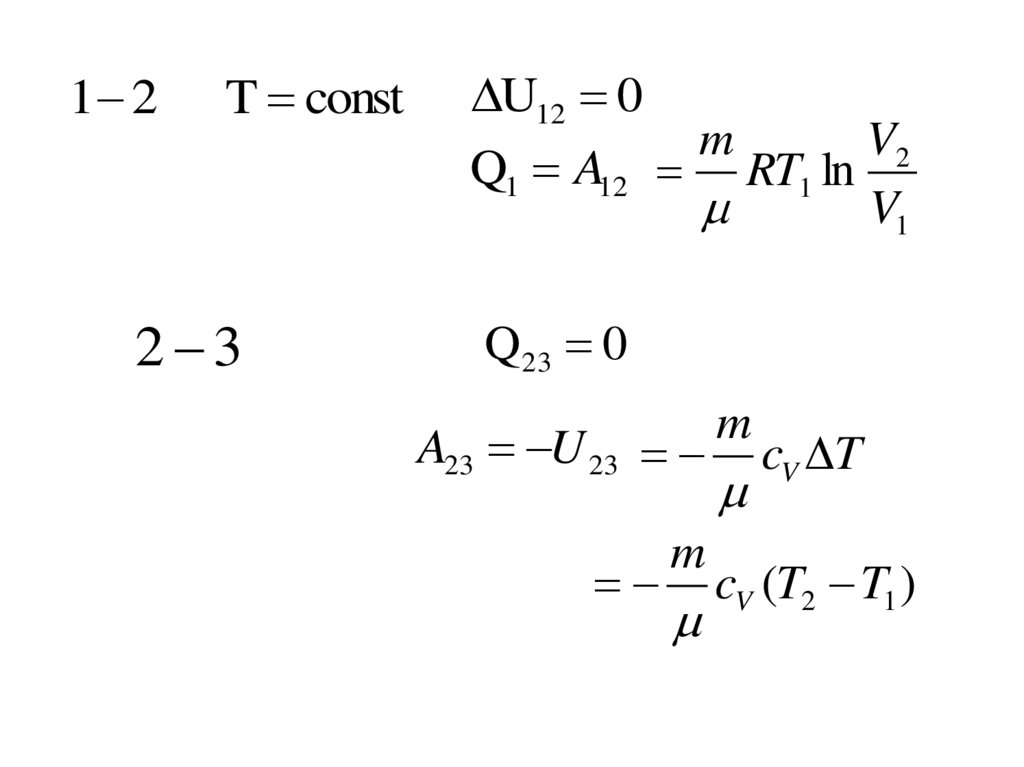
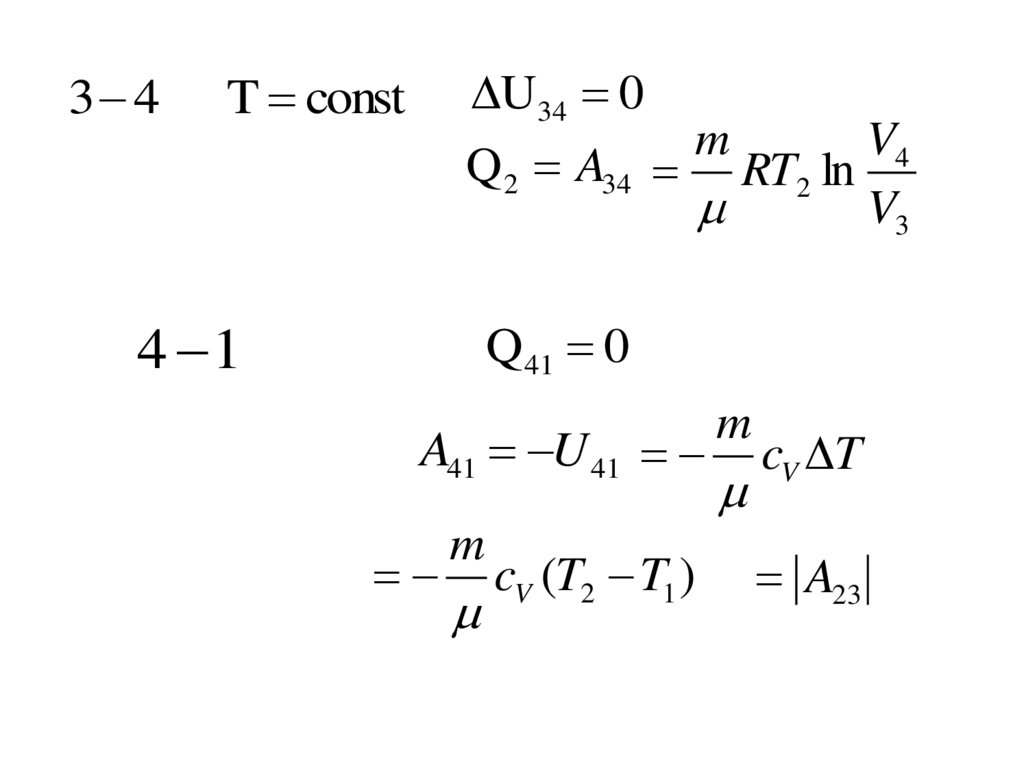
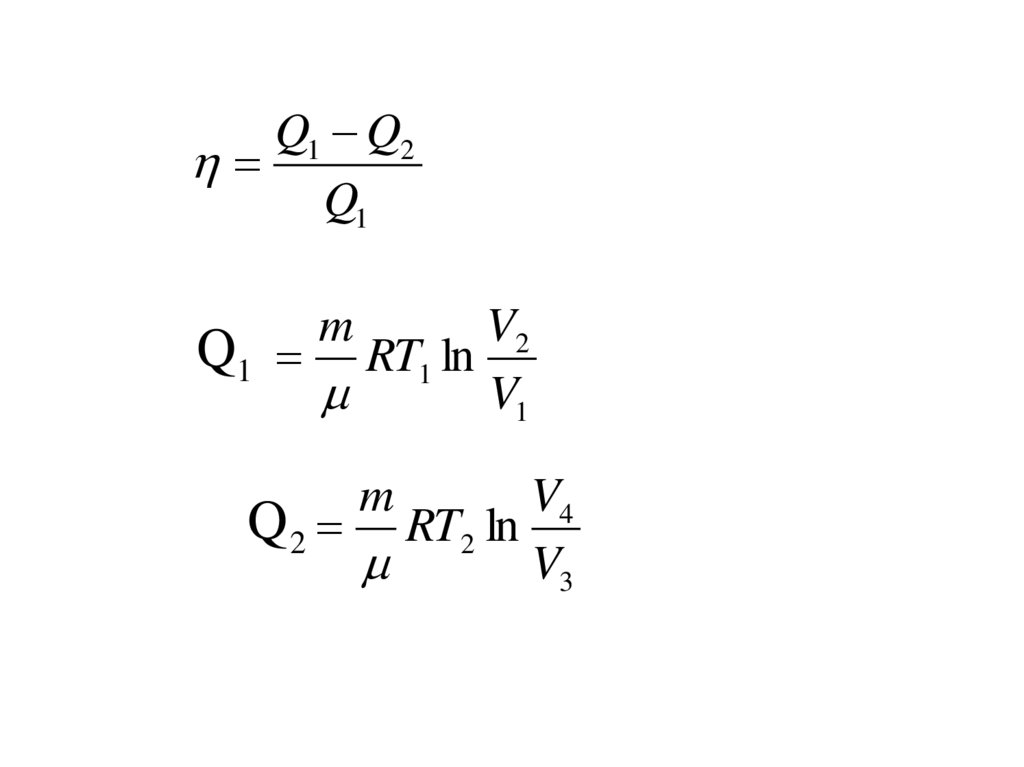

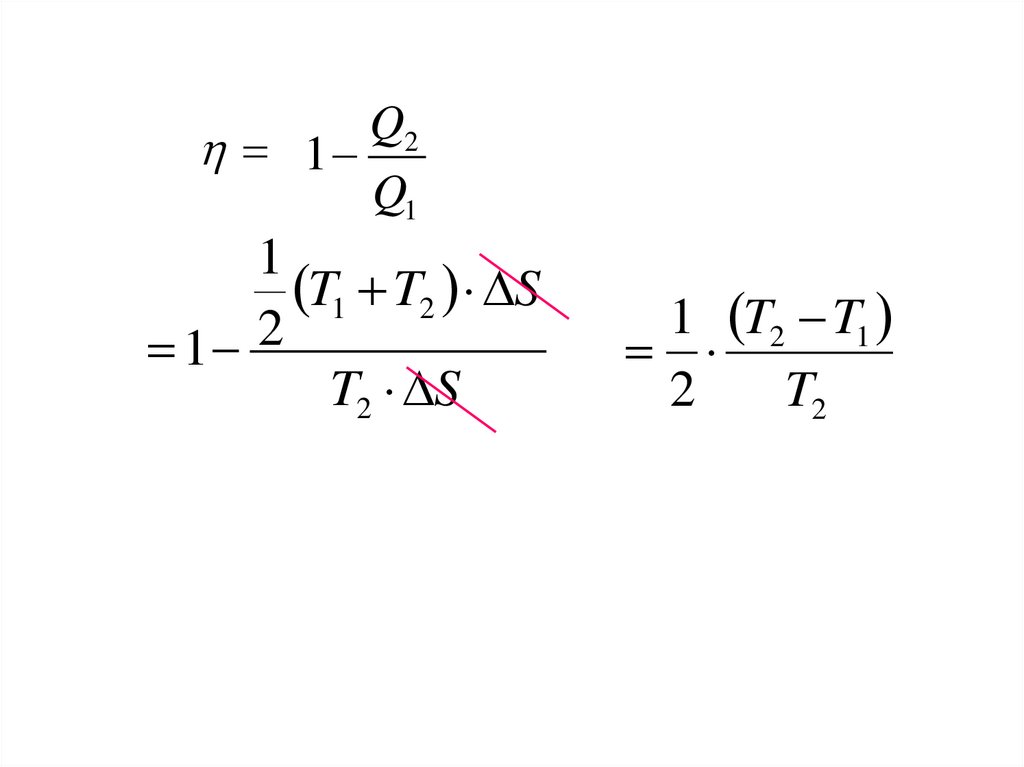
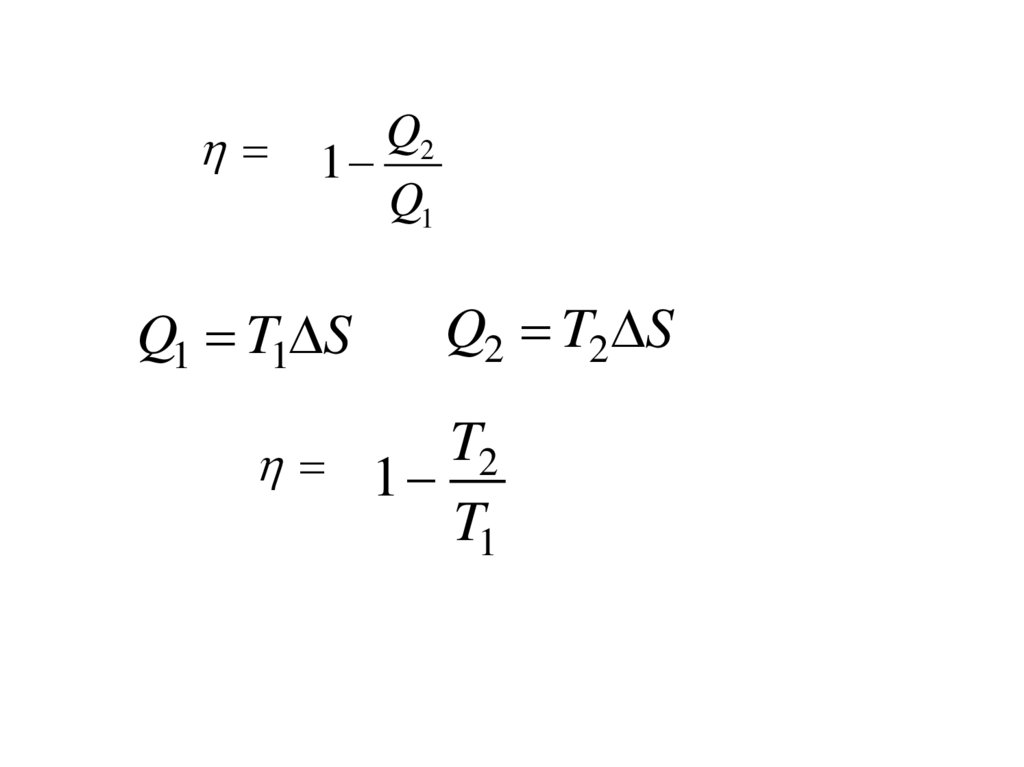
 Физика
Физика



![II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К] (Клаузиус) II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К] (Клаузиус)](https://cf3.ppt-online.org/files3/thumb/s/shTr2KkzXY6Gb1DP9c5MVIEZmtq4nJoUfBC7Ll.jpg)




