Системы уравнений и способы решения

1. СИСТЕМЫ УРАВНЕНИЙ И СПОСОБЫ РЕШЕНИЯ

2.

Актуальность: прочное освоение понятия «Система уравнений»
создаёт условия для осознанного понимания
изложения теории и решения разнообразных задач
путём отбора оптимального способа решения и
успешной подготовки к итоговой аттестации
Проблема: необходимо было решить систему уравнений
3
2 2
3
х
у
2
х
у
ху
4,
2
2
х
у
х
у
у
х 4,
но известных из школьного курса алгебры способов
решения было недостаточно

3.

Цель работы:
обобщить научные сведения по теме «Системы уравнений» и
познакомиться с новыми способами решения систем
Основные задачи:
научиться решать системы нелинейных уравнений методом
почленного умножения и деления;
рассмотреть способ введения новых переменных и
использовать его при решении систем уравнений;
изучить теорию, связанную с симметрическими системами
уравнений, и научиться решать системы такого вида;
познакомиться с понятием однородных систем уравнений и
способом их решения

4.

ЛИНЕЙНЫЕ СИСТЕМЫ
Система двух уравнений первой степени с двумя неизвестными вида
а1х + b1у = с1,
а2х + b2у = с2,
где а1, b1, с1, а2, b2, c2 – заданные числа, х, у - переменные, называется
линейной.
СПОСОБЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ
способ подстановки
графический способ
способ сложения

5.

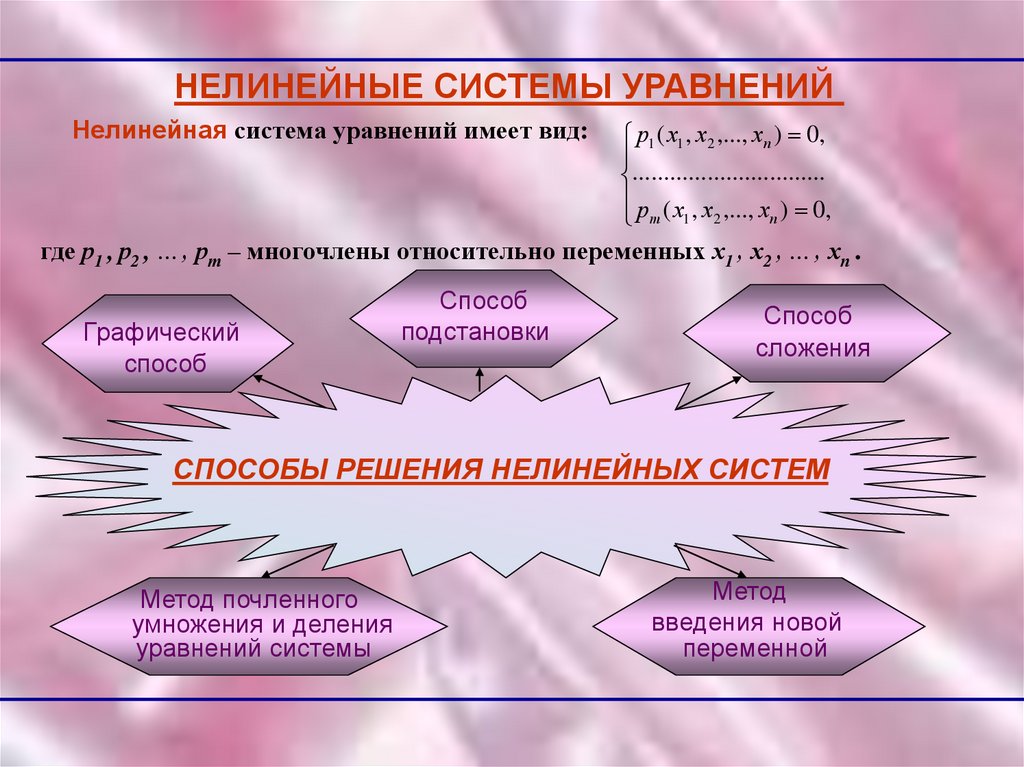
НЕЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ
Нелинейная система уравнений имеет вид:
р1 ( х1 , х2 ,..., хп ) 0,
...............................
р ( х , х ,..., х ) 0,
п
т 1 2
где р1 , р2 , …, рт – многочлены относительно переменных х1 , х2 , …, хп .
Графический
способ
Способ
подстановки
Способ
сложения
СПОСОБЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ СИСТЕМ
Метод почленного
умножения и деления
уравнений системы
Метод
введения новой
переменной

6.

СИММЕТРИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ
Система уравнений
р1 ( х1 , х2 ,..., хп ) 0,
...............................
р ( х , х ,..., х ) 0,
п
т 1 2
Теорема
Любой
называется симметрической, если все
симметрический
многочлены р1(х1, х2, …, хn), …,
многочлен от
рm(х1,х2, …, хn) являются симметрическими
переменных х1, х2, …, хn
многочленами, то есть если их значения не
может быть
изменяются при любой перестановке
представлен в виде
аргументов.
многочлена от
Основными симметрическими
основных
многочленами двух переменных х и у
симметрических
являются многочлены σ1 = х + у и σ2 = ху, а в
многочленов σ1, σ2, …, σn
трёх переменных х, у и z - многочлены
σ1 = х + у + z, σ2 = ху + уz + zх и σ3 = хуz.

7.

ОДНОРОДНЫЕ СИСТЕМЫ УРАВНЕНИЙ
Система алгебраических
уравнений от двух переменных х и у
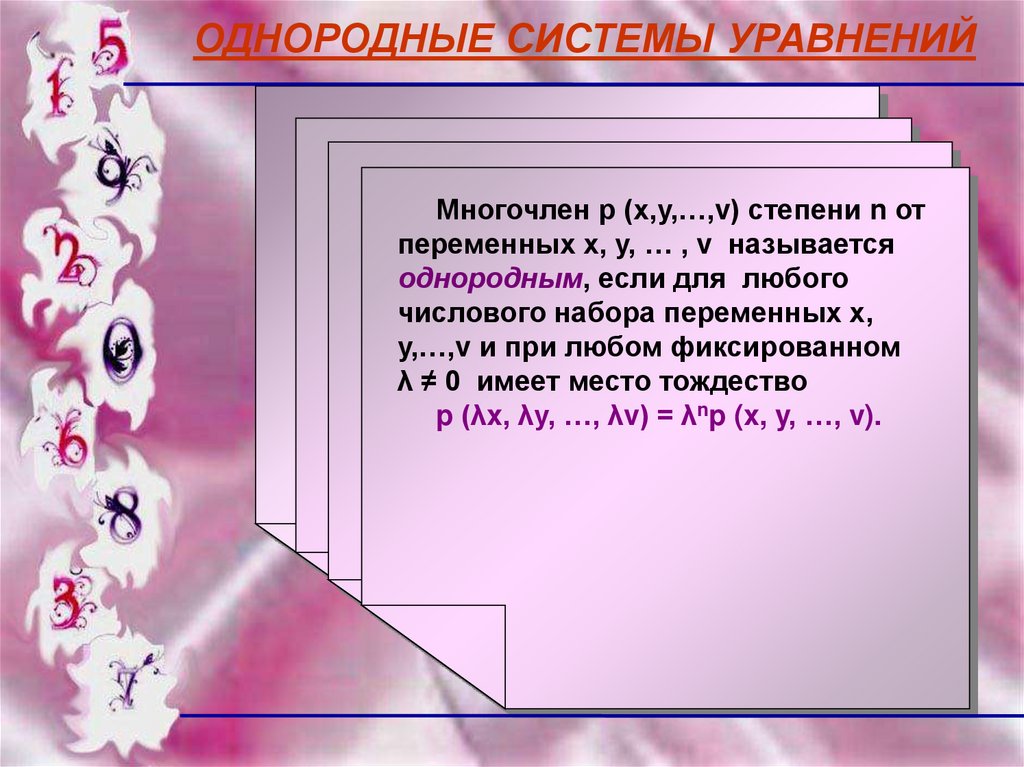
Многочлен р (х,у,…,v) степени n от
вида
переменных
х, у, … , v называется
При
решении
,
q1 x, yдля
p1 x, y если
однородным,
любого
уравнений
q1 x, y .
p2 x, yнабора
числового
переменных
однородных
При этом уравнение
р(х, у, …, v)х,= 0
у,…,v и при любом фиксированном
называется однородным
однородной,
если
называется
используется
замена:
х =уравнением
ty, у
λ ≠ 0 имеет
место тождество
многочлены
р1, р2, q1, q2 являются
степени
p (λx,n.λy,
…, λv) = λnp (x, y, …, v).
однородными,=причём
степень
tx
многочлена р1 равна степени
многочлена р2, а степень многочлена
q1 равна степени многочлена q2.

8.

Симметрические
Однородные
системы
системы
Метод введения новых
переменных

9.

Способ подстановки
При
решении
системы
двух
линейных
уравнений
с
двумя
переменными способом подстановки поступаем следующим образом:
выражаем из какого-нибудь уравнения системы одну переменную
через другую;
подставляя в другое уравнение системы вместо этой переменной
полученное выражение, решаем уравнение с одной переменной,
определяя её значение;
находим соответствующее значение второй переменной;
записываем ответ в виде пары значений (х; у)

10.

Графический способ
Алгоритм этого метода заключается в следующем:
строим графики каждого из уравнений системы;
находим координаты точки пересечения построенных графиков;
записываем в ответ координаты точки пересечения графиков уравнений

11.

Способ сложения
Суть этого метода такова:
уравниваем модули коэффициентов при одном из неизвестных;
складывая или вычитая почленно уравнения, получаем уравнение
с одной переменной, решая его, находим одно неизвестное;
подставляя найденное значение в одно из уравнений исходной
системы, находим второе неизвестное;
записываем ответ в виде пары значений (х; у)

12.

у = х2- 4х + 4
( x 2) 2 y 2 9,
Пример 1.
y x 2 4 x 4.
Перепишем данную систему в виде:
у
4
( x 2) 2 y 2 9,
y ( x 2) 2 .
0 х1
2
х2
Используя рисунок, находим приближенные
значения точек пересечения графиков: (0,4; 2,6), (3,6; 2,6).
Ответ: (0,4; 2,6), (3,6; 2,6).
(х – 2)2 + у2 =9
х

13.

Пример 2.
x y - 1,
x y 1,
2
2
2
2
2
x
xy
3
y
7
x
12
y
1
0
;
2(y - 1) y( y 1) 3 y 7( y 1) 12 y 1 0;
x y 1,
x y 1,
2
2
2
2
2
y
4
y
2
y
y
3
y
7
y
7
12
y
1
0
;
2 y 11y 5 0.
Решая второе уравнение системы 2у2 – 11у + 5 = 0, находим его корни:
у1 = 5, у2 =0,5,
Если у = 5, то х = 4; если у =0,5, то х = -0,5.
Ответ: (-0,5; 0,5), (4; 5).

14.

Пример 3. x 2 4 y 2 xy 5 y 1,
2
x 3 y 2 xy 4 y 1.
x 2 4 y 2 xy 5 y 1,
2
7 y 9 y 2,
2
Решим второе уравнение системы 7у2 - 9у + 2 = 0. Получим у1 = 7 , у2 = 1.
При подстановке у =
2
7
в первое уравнение системы, получим уравнение
49х2-14х+5=0, которое не имеет решений; при у = 1 имеем уравнение х2-х=0,
имеющее корни х=0 и х=1.
Таким образом, данная система имеет два решения (0; 1), (1; 1).
Ответ: (0; 1), (1; 1).

15.

Метод почленного умножения и деления
уравнений системы
перемножаем (делим) уравнения системы почленно, при этом получая
более простую зависимость между переменными;
объединяя полученное уравнение с одним из уравнений исходной
системы, решаем новую систему уравнений.
3
Пример 1. x xy 9,
xy xy2 6;
x(1 y)(1 y y 2 ) 9,
xy(1 y) 6.
1 у у2
у1 = 0,5, у2 = 2.
= 1,5;
у2 – 2,5у + 1 = 0
у
При у = 0,5 первое уравнение системы примет вид: х + 0,125х = 9 х = 8;
если у = 2, то х + 8х = 9, то есть х = 1.
Ответ: (8; 0,5), (1; 2).

16.

8
4 4
Пример 2. 2 x x y 1,
8
3 y x 4 y 4 2.
6(ху)8 = (ху)8 + 3(ху)4 + 2
5(ху)8 – 3(ху)4 – 2 = 0.
Пусть (ху)4 = t (t 0), тогда уравнение примет вид:
5t2 – 3t – 2 = 0 t1 = 1, t2 = - 0,4
t = - 0,4 не удовлетворяет условию t 0.
Имеем одно уравнение: (ху)4 = 1 ху = -1 или ху = 1.
ху 1,
8
4 4
Получаем совокупность систем уравнений: 2 х х у 1;
ху 1,
2 х 8 х 4 у 4 1;
Уравнение х8 = 1 имеет корни х1= -1, х2= 1.
если х = -1, то у = 1; если х = 1, то у = -1,
если х = -1, то у = -1; если х = 1, то у = 1.
Ответ: (-1; -1), (-1; 1), (1; -1), (1; 1).
ху 1,
8
2 х 2;
ху 1,
2 х 8 2;
ху 1,
8
х 1,
ху 1,
х 8 1.

17.

Метод введения новой переменной
Этапы указанного метода:
вводится новая переменная только в одно уравнение или две
новых переменных сразу для обоих уравнений;
уравнение или уравнения решаются относительно новых
переменных;
остаётся решить уже более простую систему уравнений, из
которой находим искомое решение.

18.

.
Пример.
Пусть
2 3
+ = 8,
х у
5 2
=1.
х у
ОДЗ: х 0, у 0
2t 3z 8,
1
1
а
= z, тогда система уравнений примет вид:
= t,
у
х
5t 2 z 1.
2t 3z 8, 2
5t 2 z 1; 3
4t 6 z 16,
15t 6 z 3.
19t = 19 t =1.
Если t = 1, то 2·1+3z = 8
3z = 6
z = 2.
1
1,
x
Вернёмся к переменным х и у:
1 2;
y
x 1,
y 0,5.
Пара чисел (1; 0,5) удовлетворяет ОДЗ.
Ответ: (1; 0,5).

19.

Пример. x y 5,
3
3
x y 65.
Пусть х + у = u, ху = v, тогда система уравнений примет вид:
u 5,
3
u 3uv 65;
x y 5,
xy 4;
u 5,
125 15v 65;
x 5 y,
y (5 y ) 4;
u 5,
15v 60;
u 5,
v 4.
x 5 y,
2
y 5 y 4 0;
x 5 y,
y 1,
y 4.
Ответ: (4; 1), (1; 4).
x 4,
y 1.
x 1,
y 4.

20.

2
2
Пример. x 2 xy 3 y 0,
2
x xy 2 x 3 y 6.
Если у = 0, то и х = 0, однако х = 0 и у = 0 не удовлетворяют второму
уравнению системы.
x
Пусть у ≠0. Тогда, разделив первое уравнение на у2 и полагая t = y ,
получим уравнение t2 - 2t – 3 = 0, которое имеет два корня: t1 = -1 и t2 = 3.
x
y 1,
x 2 xy 2 x 3 y 6;
x
y 3,
x 2 xy 2 x 3 y 6;
x y,
2
2
y y 2 y 3 y 6;
x 3 y,
9 y 2 3 y 2 6 y 3 y 6;
x y,
2
2 y y 6 0;
x 3 y,
2 y 2 3 y 2 0.
Корни второго уравнения первой системы у1 = 2, у2 = -1,5 х1 = - 2, х2 = 1,5.
Корни второго уравнения второй системы у1 = 2, у2 = - 0,5 х1 = 6, х2 = - 1,5.
Ответ: (-1,5; -0,5), (-2; 2), (1,5; -1,5), (6; 2).

21.

22.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Аксенова М. Д. Энциклопедия для детей Аванта +. Т.11. Математика.
2. Алимов Ш. А. Алгебра для 6-8 классов. – М.: Просвещение, 1981. – 542 с.
3. Барчунова Ф. М., Бесчинская А. А., Денищева Л. О. и др. Алгебра в 6-8 классах:
Пособие для учителя. – М.: Просвещение, 1988. – 384 с.
4. Вавилов В. В. Задачи по математике. Алгебра. – М.: Наука, 1987. – 432 с.
5. Галицкий М.Л., Гольдман А.М., Звавич Л. И. Сборник задач по алгебре для 8-9
классов. – М.: Просвещение, 1992. – 271 с.
6. Крамор В. С. Повторяем и систематизируем школьный курс алгебры и начал
анализа. – М.: Просвещение, 1990. – 416 с.
7. Никольский С. М. Математика – школьная энциклопедия. – М.: Большая
российская энциклопедия, 1996.
8. Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учебное
пособие для 10 класса средней школы. – М.: Просвещение, 1989. – 252 с.
9. Яковлева Г. Н. Пособие по математике для поступающих в вузы. – М.: Наука,
1982.– 608 с.
10. «Симметрические системы»
www.college.ru/mathematics/courses/algebra/content/chapter.