Похожие презентации:
Теорема Пифагора. Решение задач
1.
2.
В прямоугольном треугольникеквадрат гипотенузы равен
сумме квадратов катетов.
С
Выразить гипотенузу АВ
АВ2 = АС2 + ВС2
АВ АС СВ
2
А
2
В
Выразить катет АС
Выразить катет ВС
АС2 = АВ2 –СВ2
АС АВ СВ
2
ВС2 = АВ2 –СА2
2
ВС АВ2 СА2
3.
Блиц-опрос – УСТНАЯ РАБОТАОпределить углы треугольника со сторонами 1,
2 – большая сторона
2
2
3 1
2
3, 2
900
3
1
2
300
600
2
ЗНАЧИТ: Треугольник – прямоугольный,
гипотенуза 2,
катеты 1 и
Углы треугольника 900, 600, 300, т.к. катет, равный 1, в два
раза меньше гипотенузы 2.
3
4.
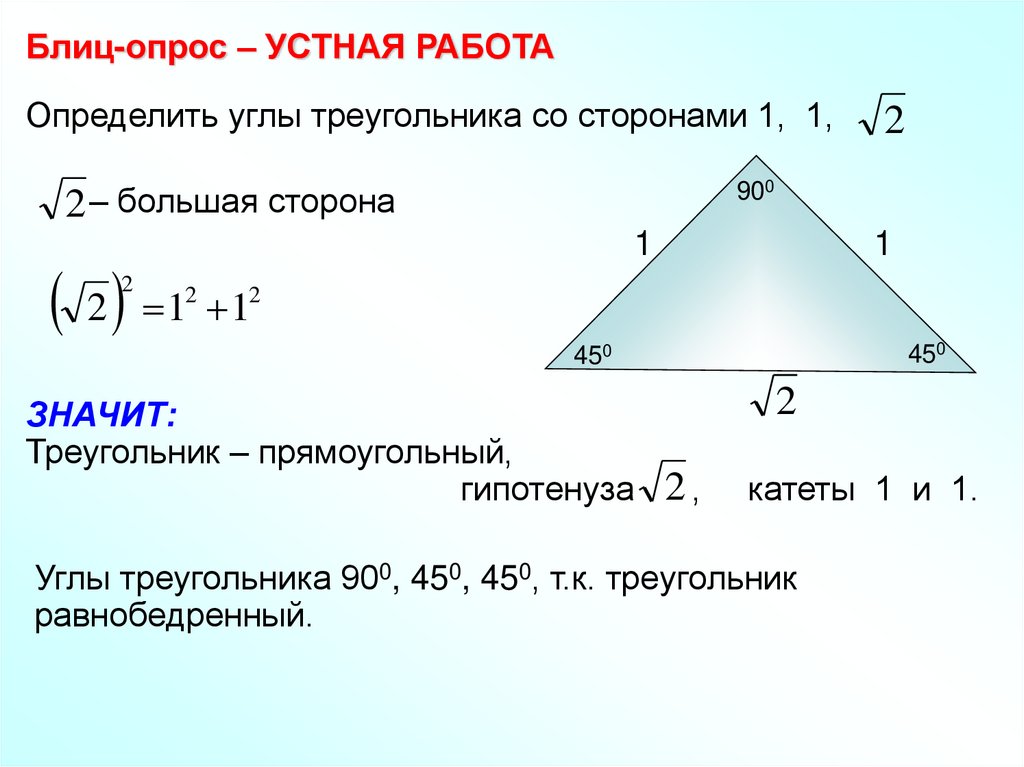
Блиц-опрос – УСТНАЯ РАБОТАОпределить углы треугольника со сторонами 1, 1,
900
2 – большая сторона
1
2 1 1
2
2
2
1
2
450
450
ЗНАЧИТ:
Треугольник – прямоугольный,
гипотенуза 2 ,
2
катеты 1 и 1.
Углы треугольника 900, 450, 450, т.к. треугольник
равнобедренный.
5.
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
х
D
В
4
3
О
А
С
6.
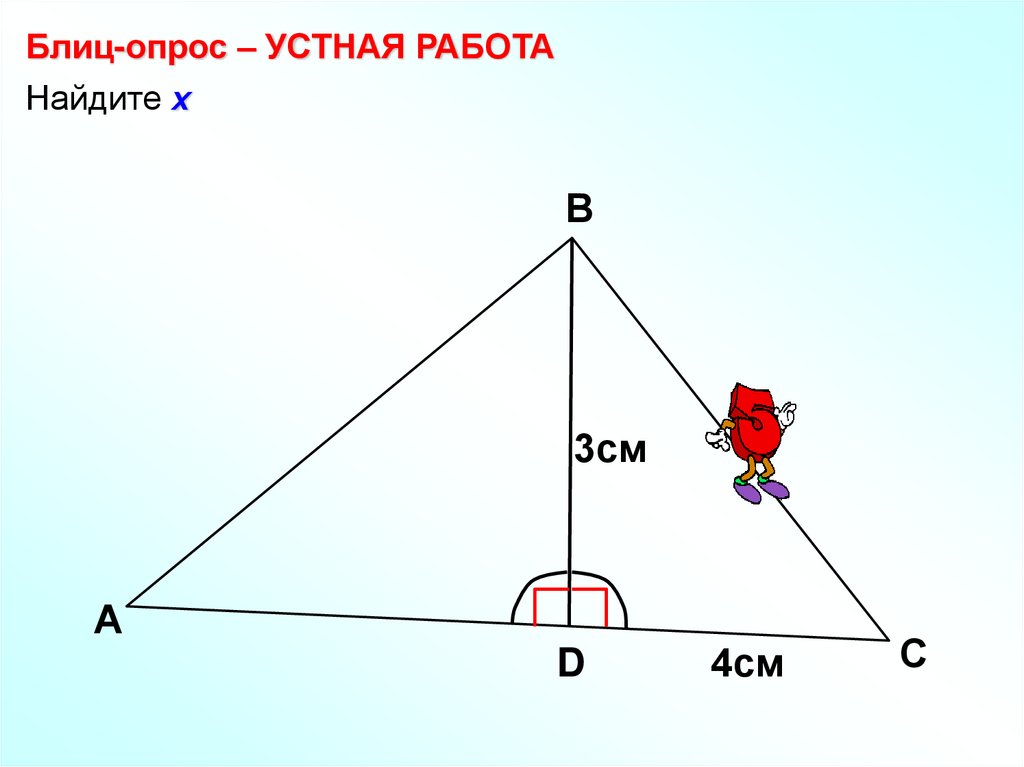
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
В
3см
А
D
х
4см
С
7.
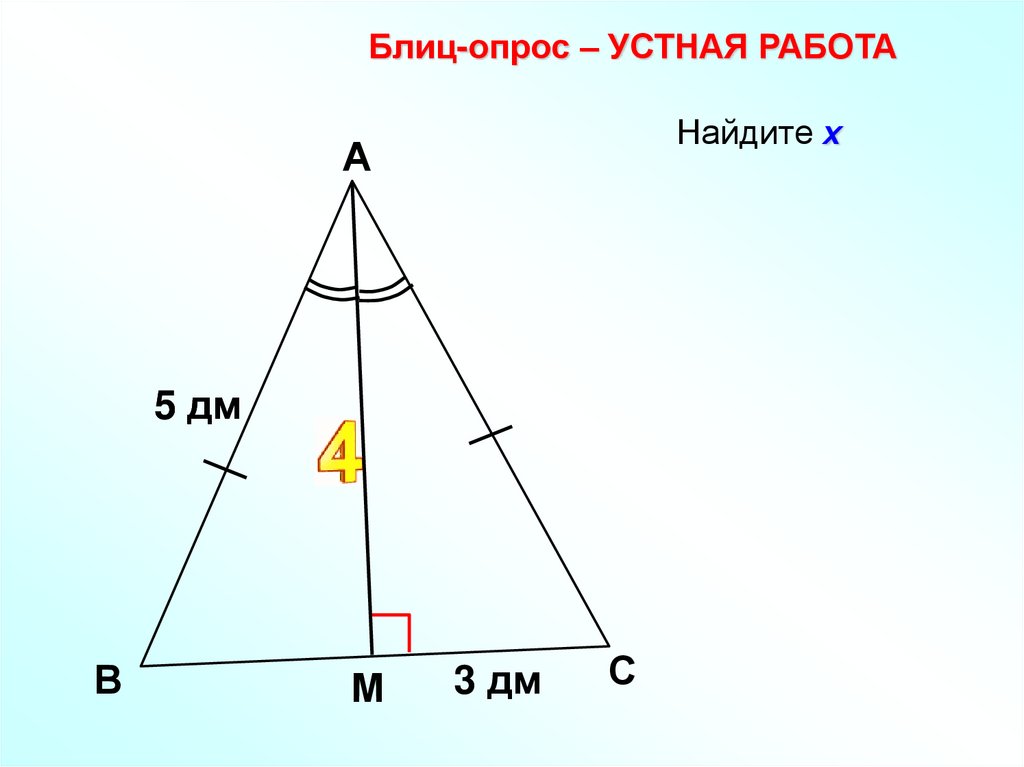
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
А
5 дм
х
В
М
3 дм
С
8.
Блиц-опрос – УСТНАЯ РАБОТАa II b
Найдите х
А
5 дм
a
4 дм
b
В
х
С
9.
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
АС = 6 см, ВD = 8 см.
В
х
4
А
О
3
D
С
10.
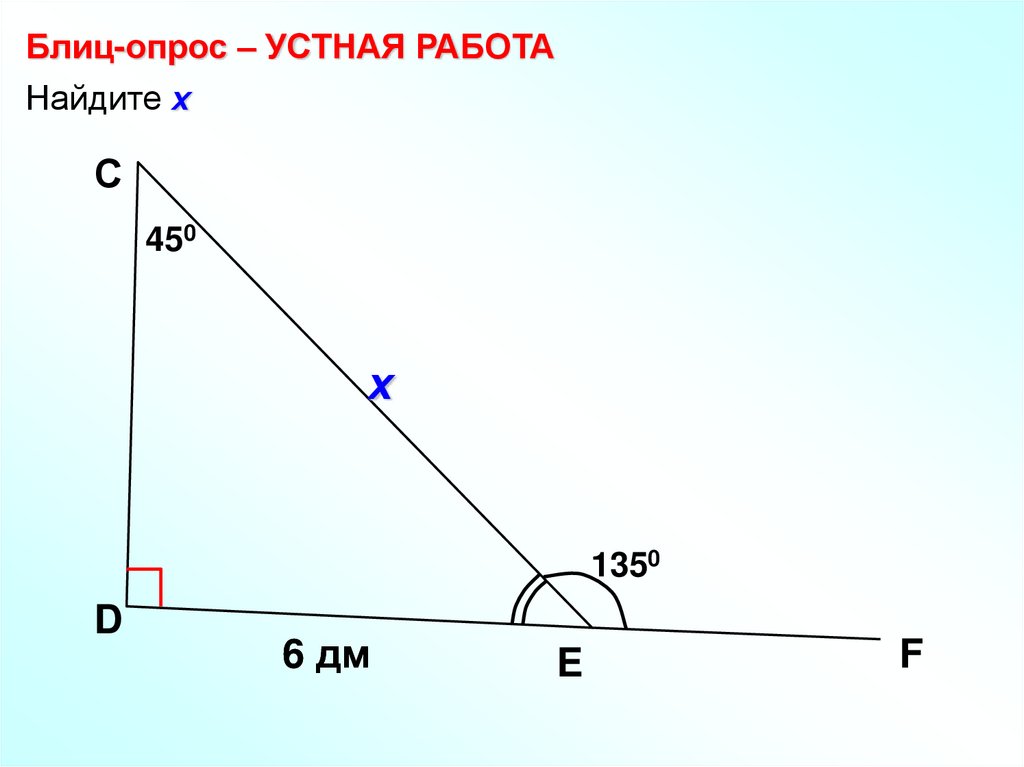
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
С
450
х
1350
D
6 дм
E
F
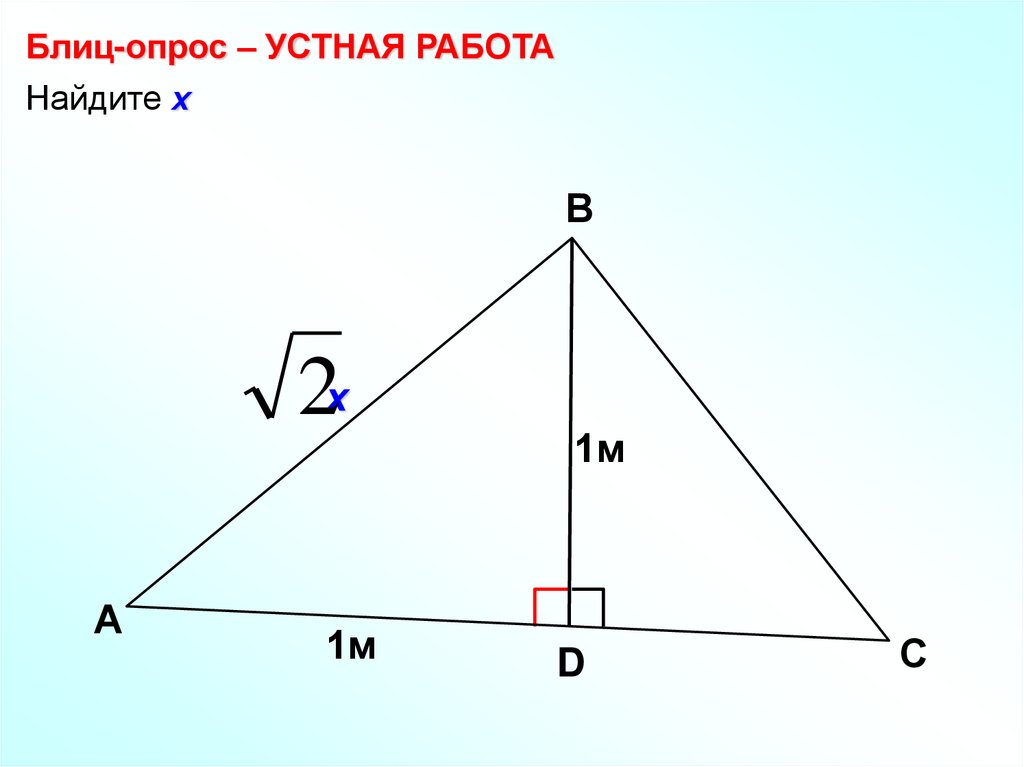
11.
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
В
2х
А
1м
1м
D
С
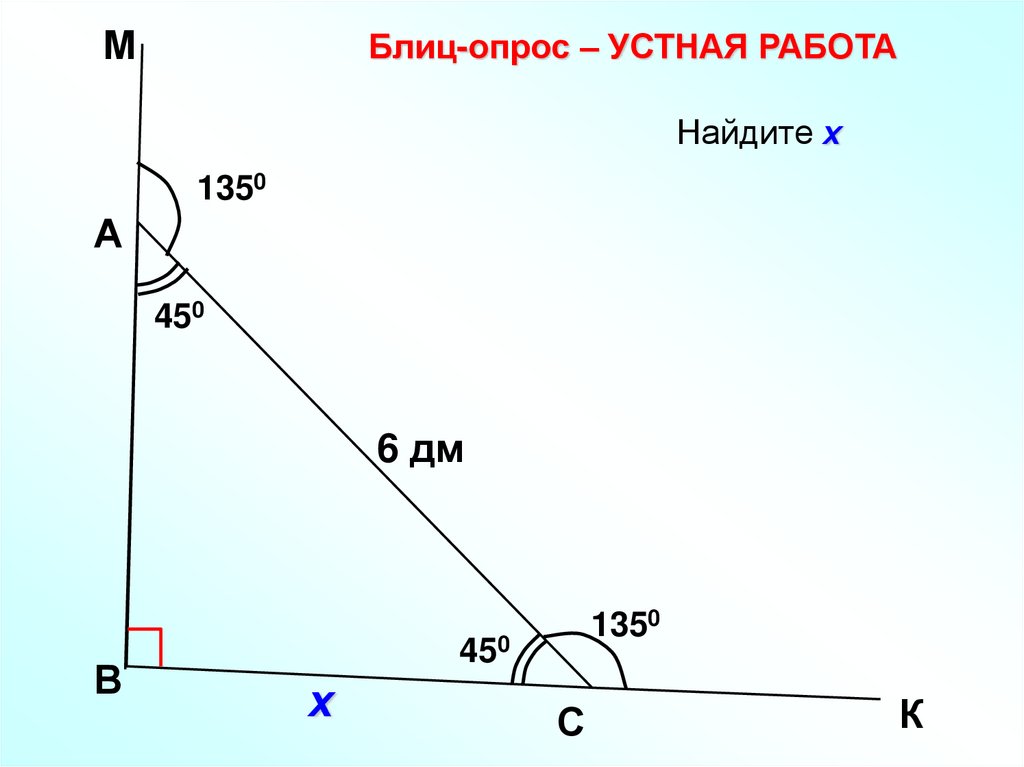
12.
МБлиц-опрос – УСТНАЯ РАБОТА
Найдите х
1350
А
450
6 дм
В
1350
450
х
С
К
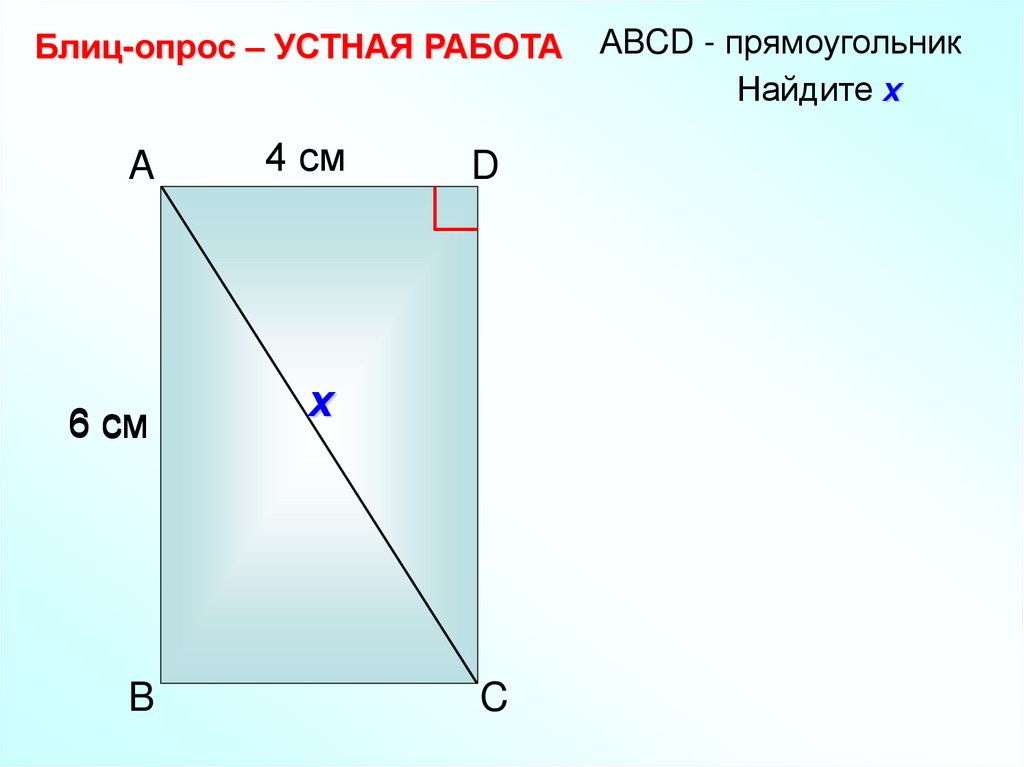
13.
Блиц-опрос – УСТНАЯ РАБОТАA
6 см
B
4 см
D
х
C
АBCD - прямоугольник
Найдите х
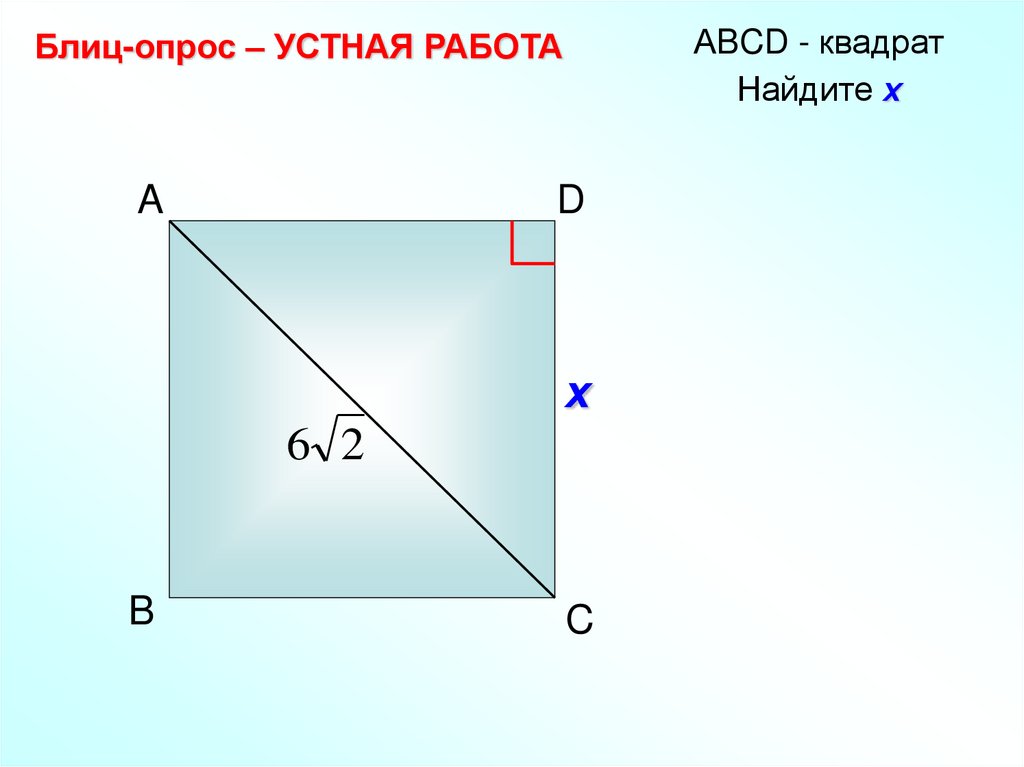
14.
АBCD - квадратНайдите х
Блиц-опрос – УСТНАЯ РАБОТА
A
D
х
6 2
B
х
C
15.
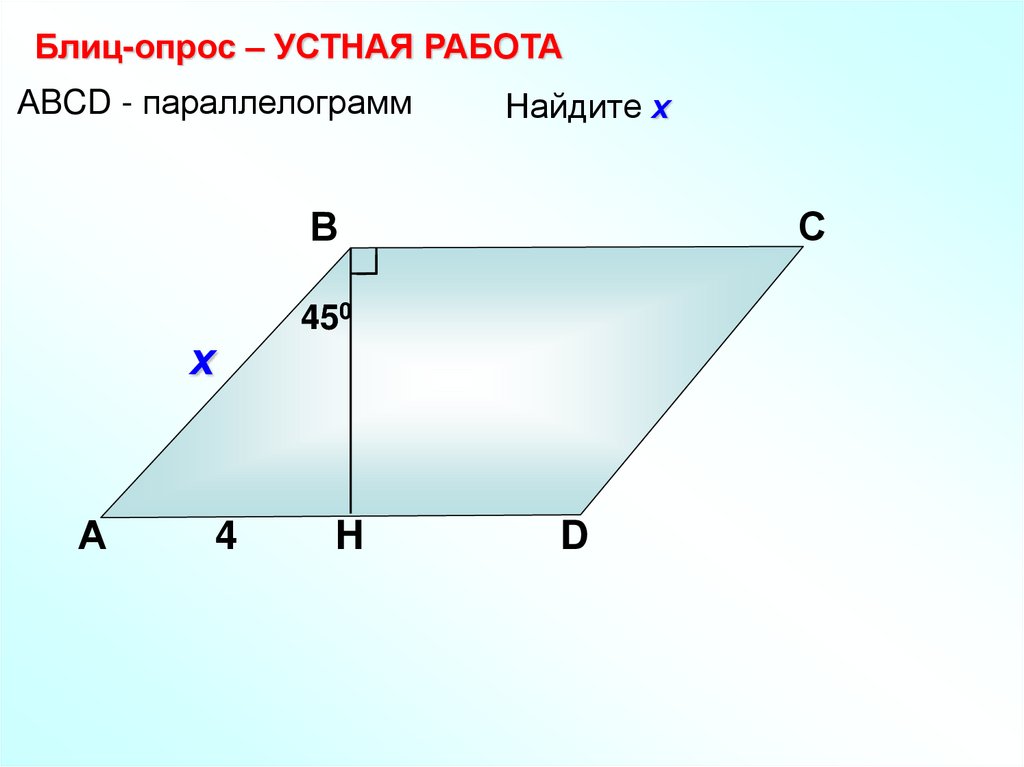
Блиц-опрос – УСТНАЯ РАБОТААBCD - параллелограмм
Найдите х
В
450
х
А
С
4
H
D
16.
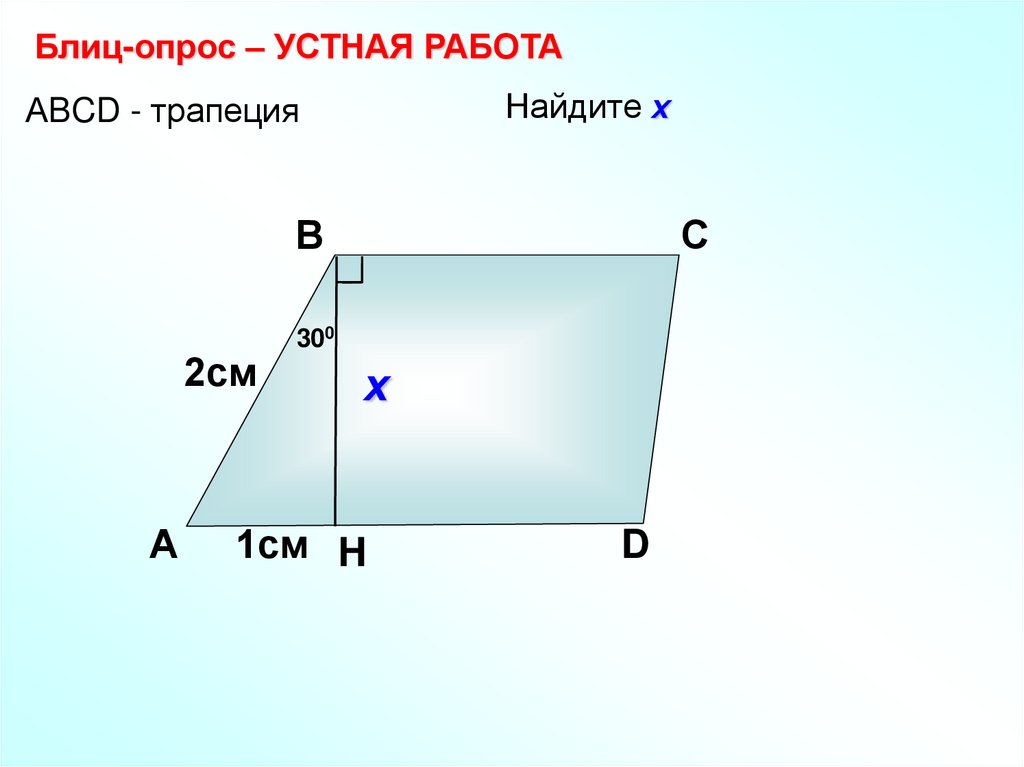
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
АBCD - трапеция
В
2см
А
С
300
х
1см H
D
17.
Блиц-опрос – УСТНАЯ РАБОТАНайдите х
АBCD - трапеция
С
В
х
А
4дм
2дм
H
D
18.
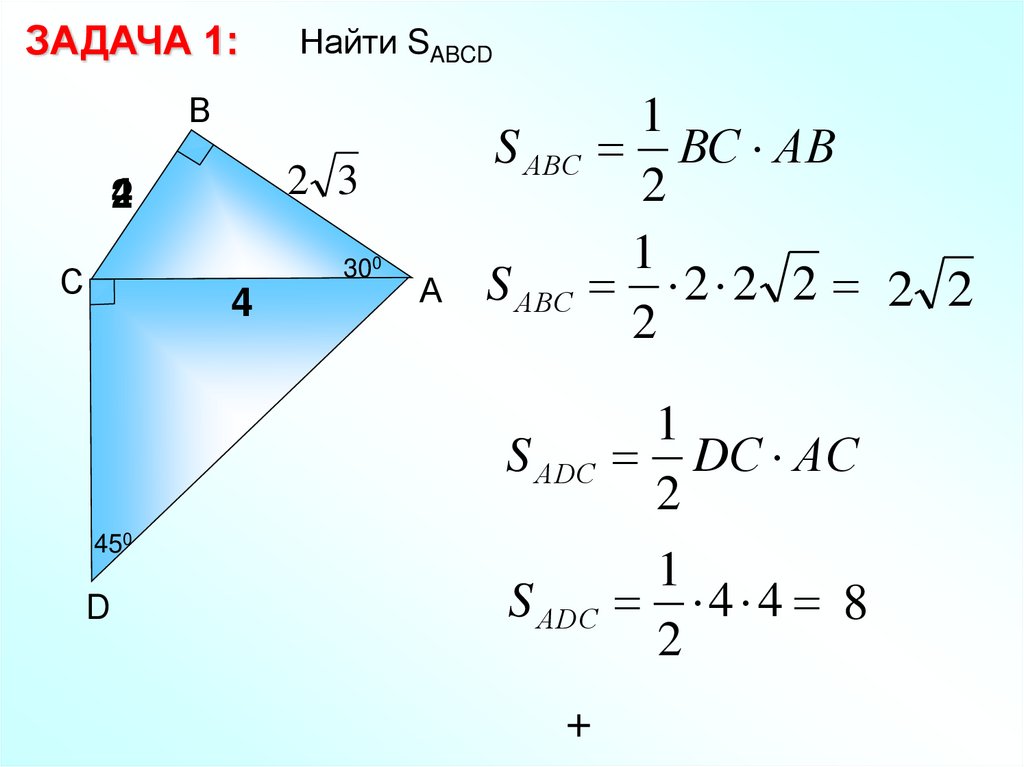
ЗАДАЧА 1:Найти SABCD
В
2 3
4
2
300
С
4
А
1
S АВС ВС АВ
2
1
S АВС 2 2 2 2 2
2
S АDС
1
DС АC
2
S АDС
1
4 4 8
2
450
D
+
19.
ЗАДАЧА 2:На стороне АВ квадрата АВСD, равной 12 см, отмечена
точка М так, что МС = 13 см. Найдите площадь
четырехугольника АМСD.
В
12
С
13
М
А
12
12
D
20.
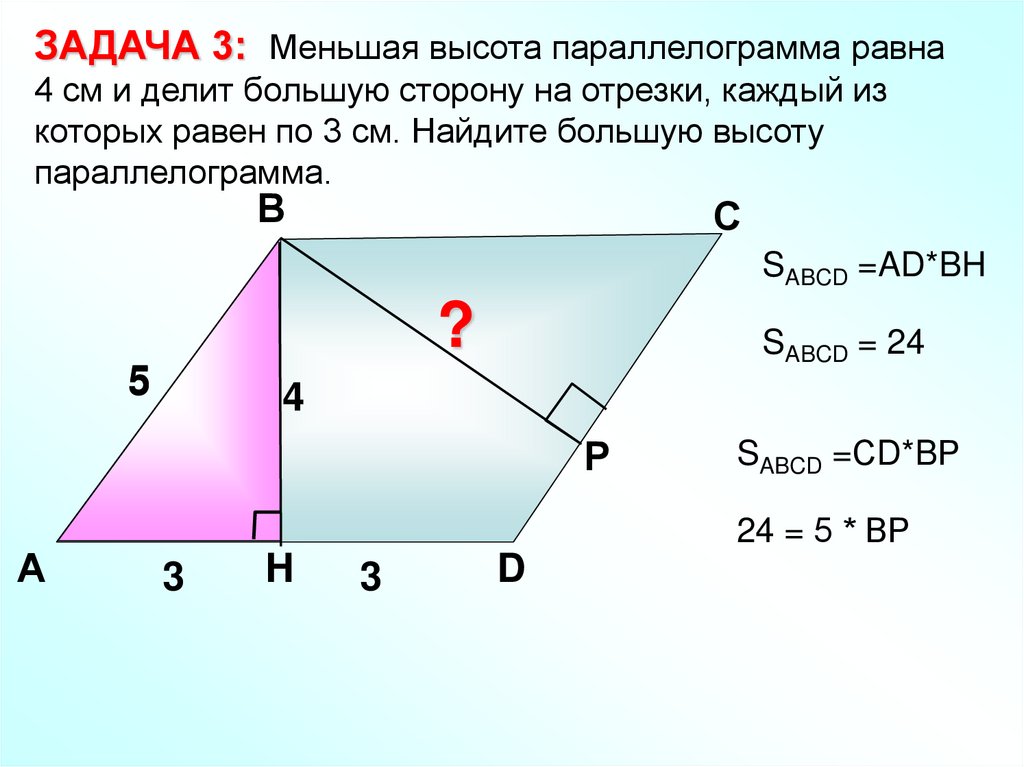
ЗАДАЧА 3: Меньшая высота параллелограмма равна4 см и делит большую сторону на отрезки, каждый из
которых равен по 3 см. Найдите большую высоту
параллелограмма.
В
С
SABCD =AD*BH
?
5
SABCD = 24
4
Р
А
SABCD =СD*BР
24 = 5 * ВР
3
H
3
D
21.
ЗАДАЧА 4: Катеты прямоугольного треугольникаотносятся как 3 : 4, а гипотенуза равна 15 см. Найдите
периметр треугольника.
(3х)2 + (4х)2 = 152
С
9х2 + 16х2 = 225
3х
4х
25х2 = 225
х2 = 9
х=3
A
15
Стороны треугольника 9, 12, 15.
В
22.
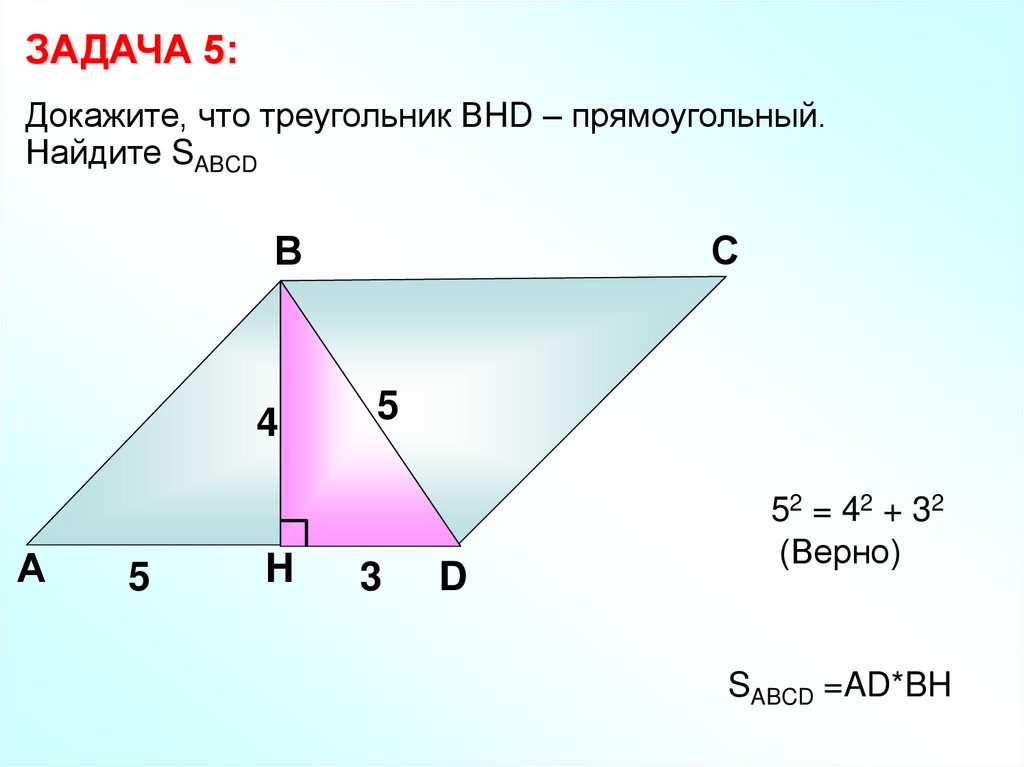
ЗАДАЧА 5:Докажите, что треугольник ВHD – прямоугольный.
Найдите SABCD
В
4
А
5
H
С
5
3
D
52 = 42 + 32
(Верно)
SABCD =AD*BH
23.
ЗАДАЧА 6:Найдите площадь трапеции АВCD
с основаниями АD и ВС.
102 = 82 + 62
В
6
А
(Верно)
С
5
10
8
S АВСD
D
1
( АD BC ) ВA
2
24.
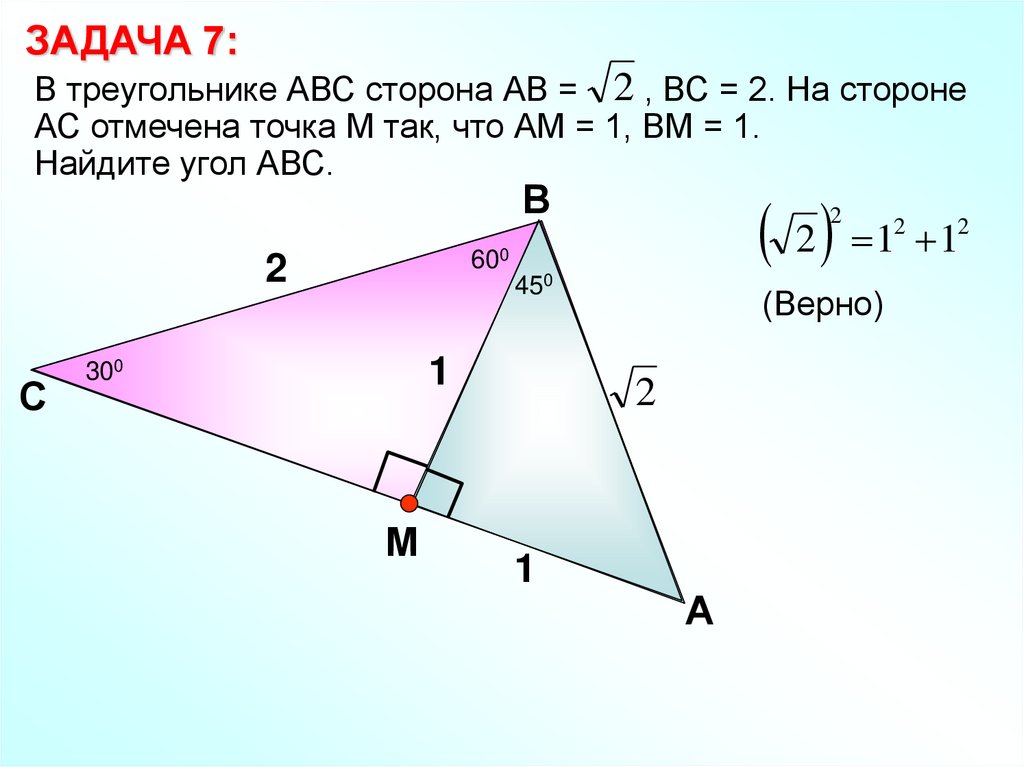
ЗАДАЧА 7:В треугольнике АВС сторона АВ = 2 , ВС = 2. На стороне
АС отмечена точка М так, что АМ = 1, ВМ = 1.
Найдите угол АВС.
2 1 1
450
(Верно)
2
600
2
С
В
1
300
М
2
1
А
2
2
25.
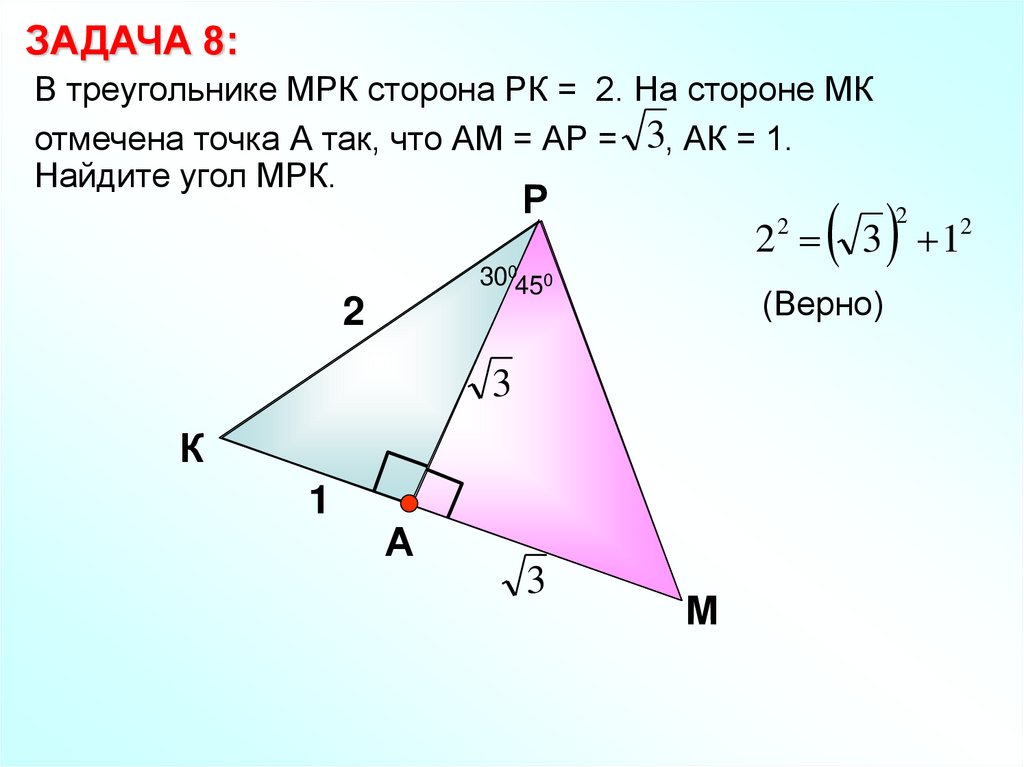
ЗАДАЧА 8:В треугольнике МРК сторона РК = 2. На стороне МК
отмечена точка А так, что АМ = АР = 3, АК = 1.
Найдите угол МРК.
Р
2
2
300450
2
(Верно)
3
К
1
А
3
3 1
М
2
2
26.
ЗАДАЧА 9:В треугольнике АВС угол А равен 450, угол С – тупой,
ВС = 17 см. На продолжении стороны АС за точку С взята
точка D так, что CD = 8 см, BD = 15 см.
Докажите, что треугольник ВСD – прямоугольный.
Найдите SABC
В
17 2 152 82
17
(Верно)
15
450
А
С
8
D
S АВC
1
АC ВD
2
27.
ЗАДАЧА 10:№ 517 из учебника
Найдите площадь четырехугольника АВСD, в котором
АВ = 5 см, ВС = 13 см, СD = 9 см, DA = 15 см, АС = 12 см.
132 122 52
В
(Верно)
13
5
S АВС
1
АВ АС
2
12
А
S АDС
1
АС DС
2
152 122 92
(Верно)
С
9
15
D
28.
ЗАДАЧА 11:А
5 см
Найдите площадь треугольника
со сторонами 6 см, 5 см, 5 см.
5 см
4
В
М
6 см
3
S АВС
С
1
ВС АМ
2
29.
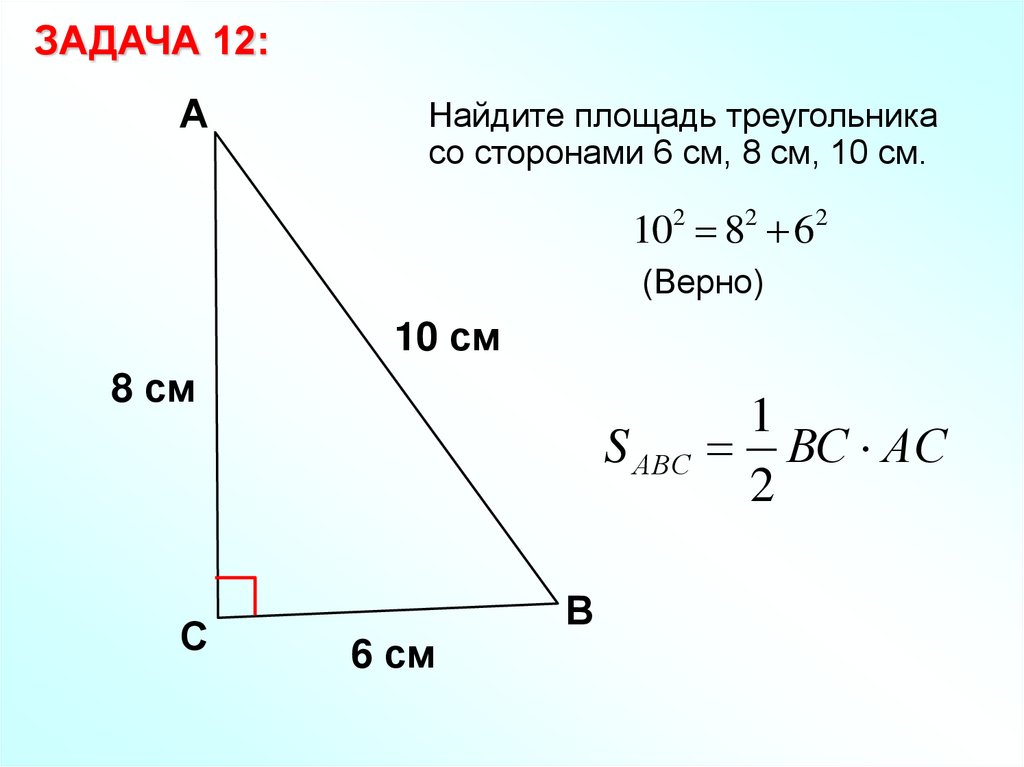
ЗАДАЧА 12:А
Найдите площадь треугольника
со сторонами 6 см, 8 см, 10 см.
102 82 62
(Верно)
10 см
8 см
S АВС
С
6 см
В
1
ВС АС
2
30.
ЗАДАЧА 13:ABCD – прямоугольная трапеция.
Найдите площадь ABCD
В
10
А
8
1
SABCD = (ВС + AD) * ВН
2
3
С
6
H
D
31.
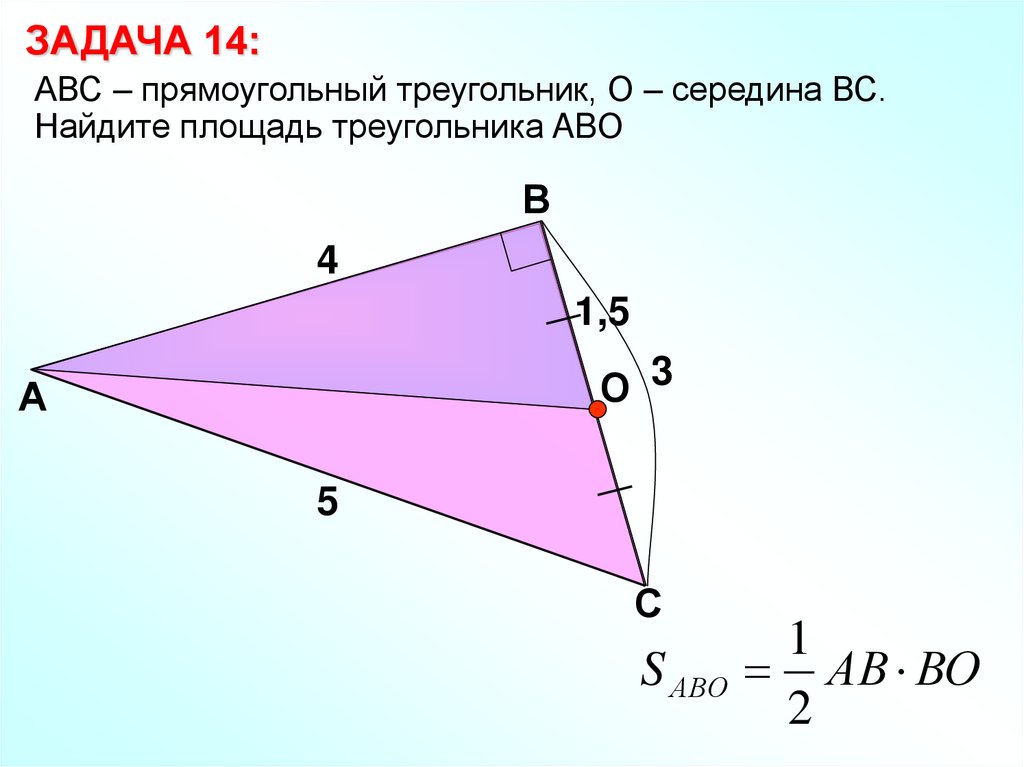
ЗАДАЧА 14:АВС – прямоугольный треугольник, О – середина ВС.
Найдите площадь треугольника ABО
В
4
1,5
О 3
А
5
С
S АВО
1
АВ ВО
2
32.
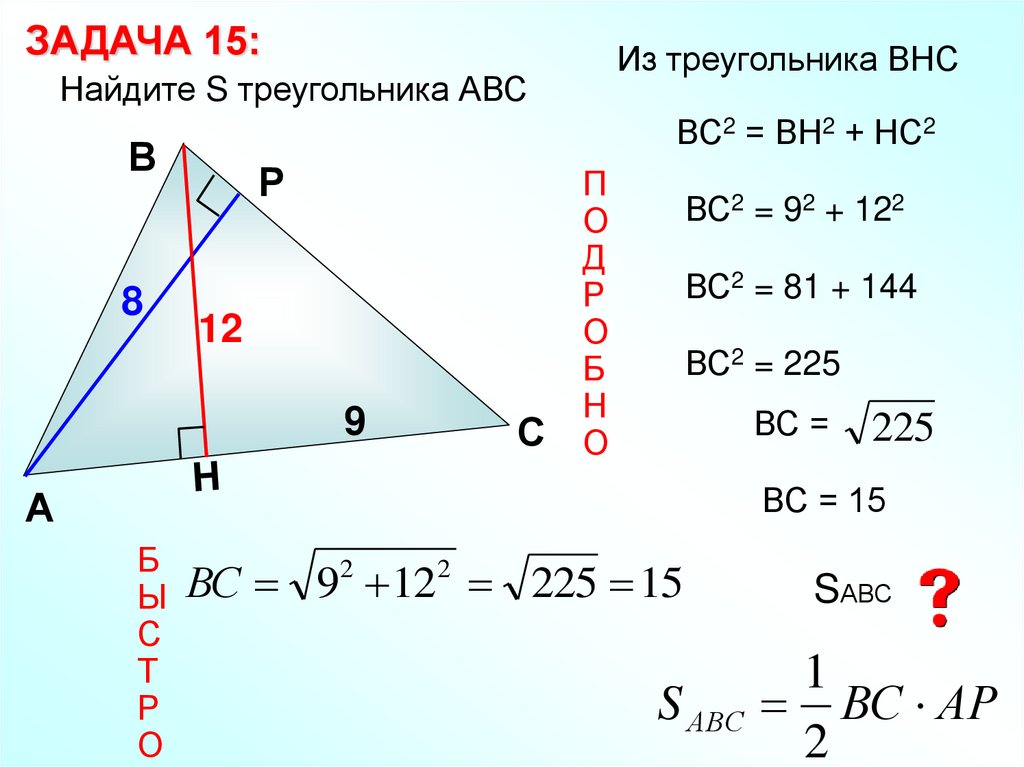
ЗАДАЧА 15:Из треугольника ВНС
Найдите S треугольника АВС
ВС2 = ВН2 + НС2
В
8
Р
12
9
С
П
О
Д
Р
О
Б
Н
О
ВС2 = 92 + 122
ВС2 = 81 + 144
ВС2 = 225
ВС =
225
ВС = 15
А
Б
Ы
С
Т
Р
О
ВС 92 122 225 15
S АВС
SАВС
1
ВС АР
2
33.
ЗАДАЧА 16:Диагонали некоторой трапеции равны 5 см и 12 см, а
основания 3 см и 10 см. Найдите углы между
диагоналями этой трапеции.
В
12
А
10
132 = 122 + 52
(Верно)
С
3
5
D
F















 Математика
Математика








