Аксиомы стереометрии

1.

Определение
Аксиома – это утверждение не требующее
доказательства.

2.

Определение
Аксиомы стереометрии – утверждения о свойствах
геометрических тел, принимаемые в качестве исходных
положений, на основе которых доказываются все теоремы и
вообще строится вся геометрия.

3.

Аксиома A1
Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
B
A
C
Если C ∉ AB, то ∃α:
A, B, C ∊ α,
причем α – единственная.

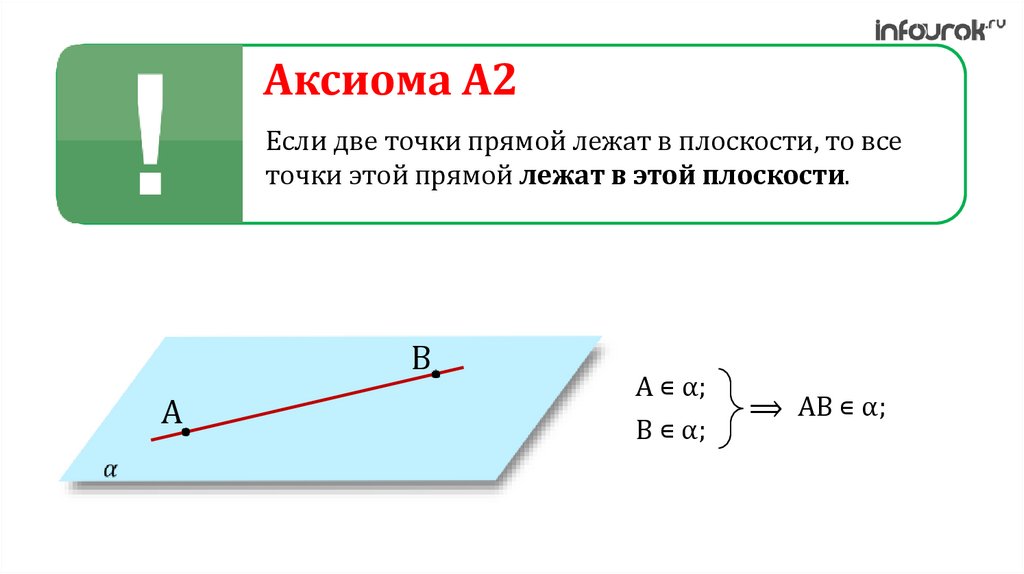
4.

Аксиома A2
Если две точки прямой лежат в плоскости, то все
точки этой прямой лежат в этой плоскости.
B
A
A ∊ α;
B ∊ α;
⟹ AB ∊ α;

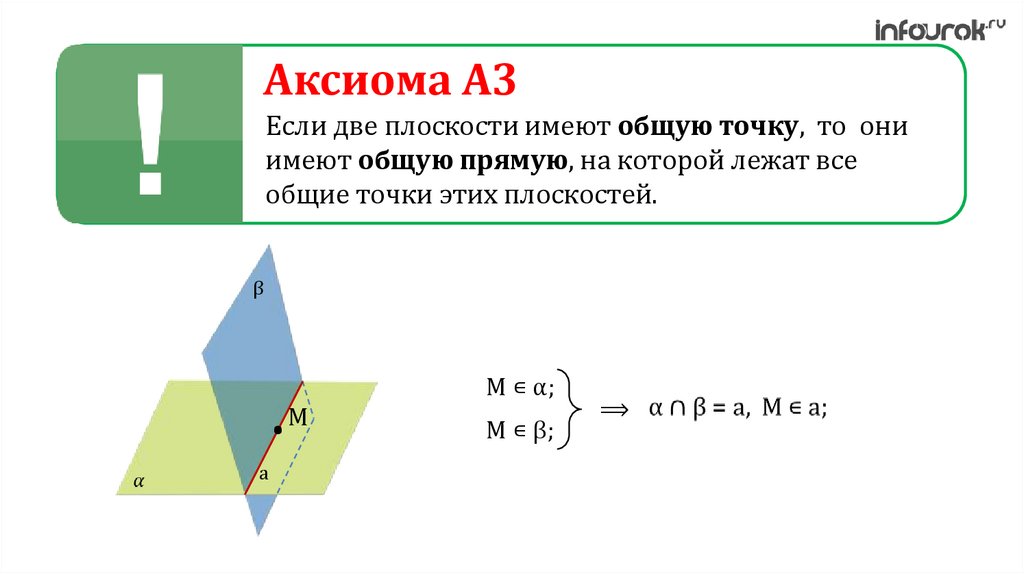
5.

Аксиома A3
Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все
общие точки этих плоскостей.
β
M
a
M ∊ α;
M ∊ β;
⟹

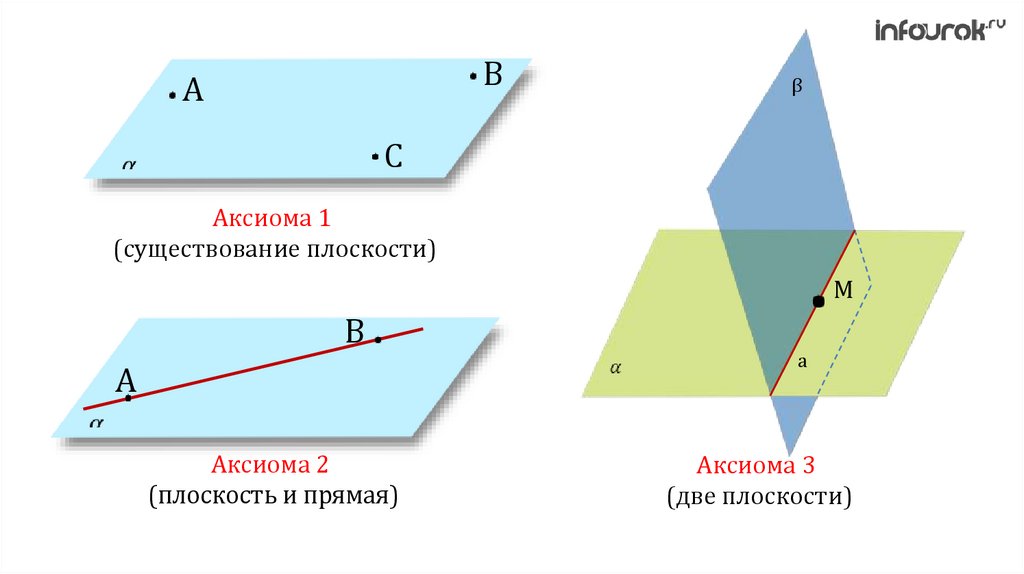
6.

B
A
β
C
Аксиома 1
(существование плоскости)
M
B
A
Аксиома 2
(плоскость и прямая)
a
Аксиома 3
(две плоскости)

7.

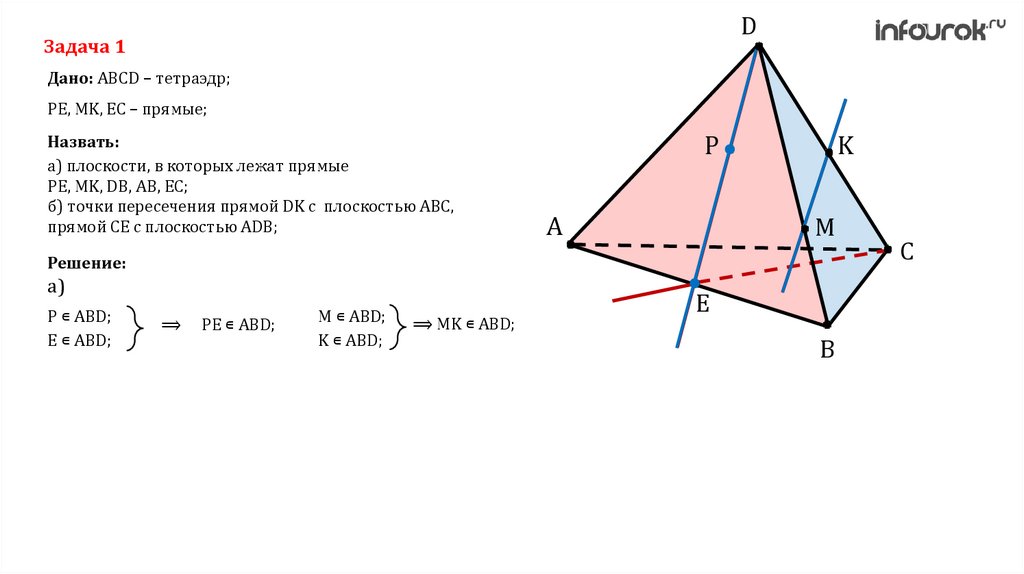
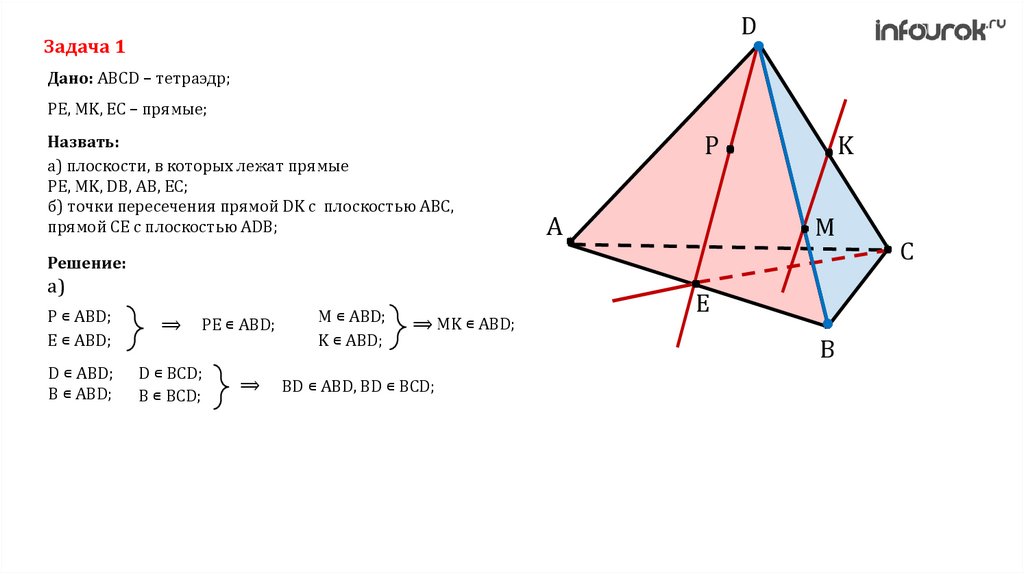
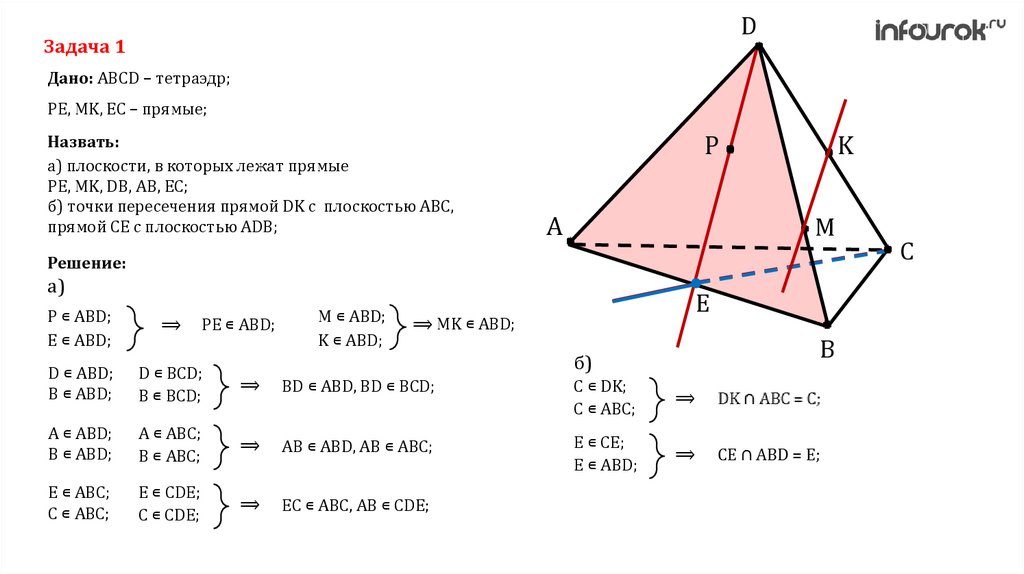
D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
P ∊ ABD;
E ∊ ABD;
⟹
PE ∊ ABD;
M ∊ ABD;
K ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

8.

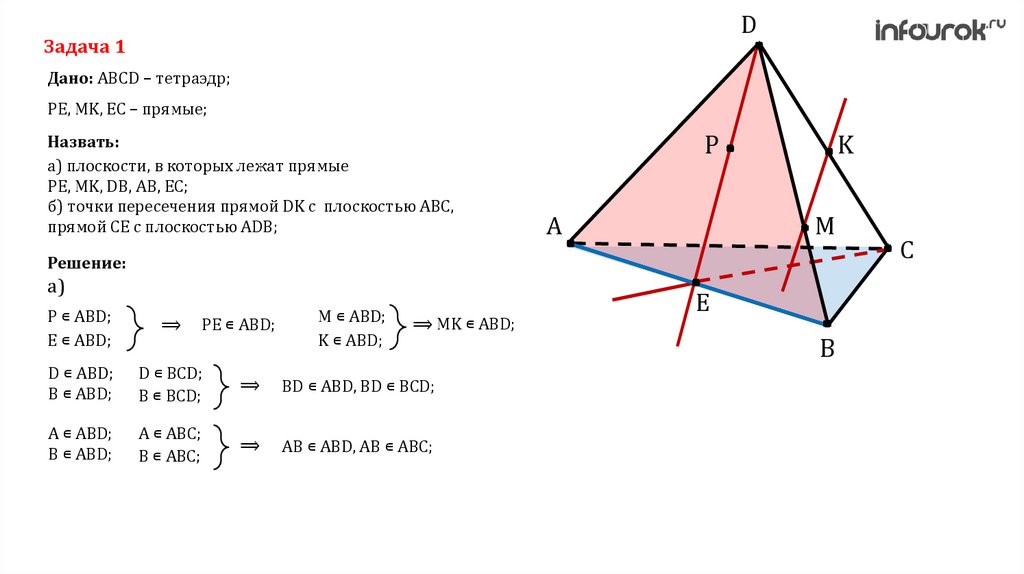
D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
PE ∊ ABD;
⟹
M ∊ ABD;
K ∊ ABD;
⟹ MK ∊ ABD;
BD ∊ ABD, BD ∊ BCD;
E
B
C

9.

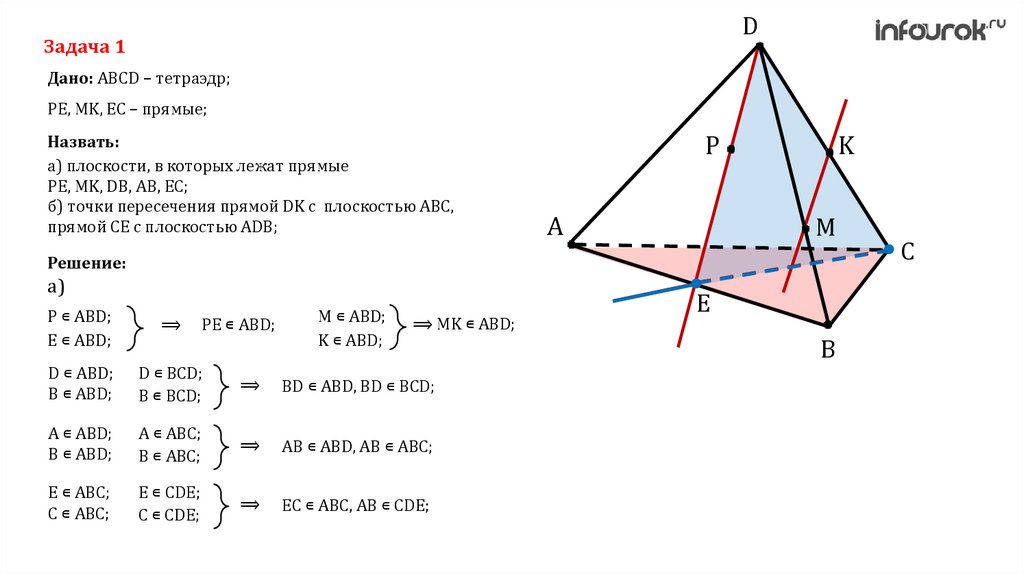
D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
PE ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

10.

D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
⟹ MK ∊ ABD;
E
B
C

11.

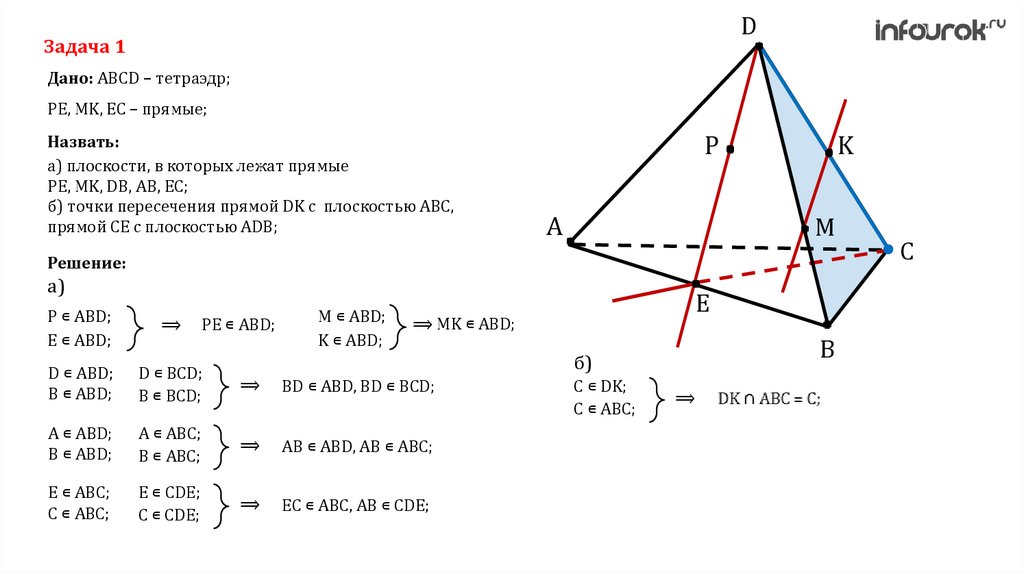
D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
E
⟹ MK ∊ ABD;
B
б)
С ∊ DK;
C ∊ ABC;
⟹
C

12.

D
Задача 1
Дано: ABCD – тетраэдр;
PE, MK, EC – прямые;
Назвать:
а) плоскости, в которых лежат прямые
PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью ABC,
прямой CE с плоскостью ADB;
P
A
K
M
Решение:
а)
M ∊ ABD;
K ∊ ABD;
E
P ∊ ABD;
E ∊ ABD;
⟹
D ∊ ABD;
B ∊ ABD;
D ∊ BCD;
B ∊ BCD;
⟹
BD ∊ ABD, BD ∊ BCD;
С ∊ DK;
C ∊ ABC;
⟹
A ∊ ABD;
B ∊ ABD;
A ∊ ABC;
B ∊ ABC;
⟹
AB ∊ ABD, AB ∊ ABC;
E ∊ CE;
E ∊ ABD;
⟹
E ∊ ABC;
C ∊ ABC;
E ∊ CDE;
C ∊ CDE;
⟹
EC ∊ ABC, AB ∊ CDE;
PE ∊ ABD;
⟹ MK ∊ ABD;
B
б)
C

13.

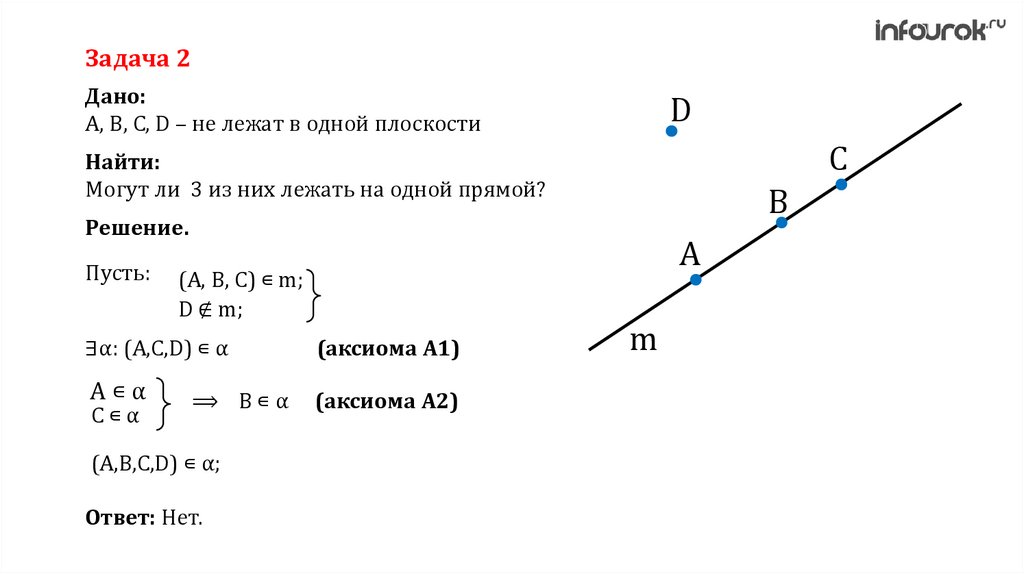
Задача 2
Дано:
A, B, C, D – не лежат в одной плоскости
D
C
Найти:
Могут ли 3 из них лежать на одной прямой?
B
Решение.
Пусть:
A
(A, B, C) ∊ m;
D ∉ m;
∃α: (A,C,D) ∊ α
(аксиома A1)
A∊α
(аксиома A2)
C∊α
⟹ B∊α
(A,B,C,D) ∊ α;
Ответ: Нет.
m

14.

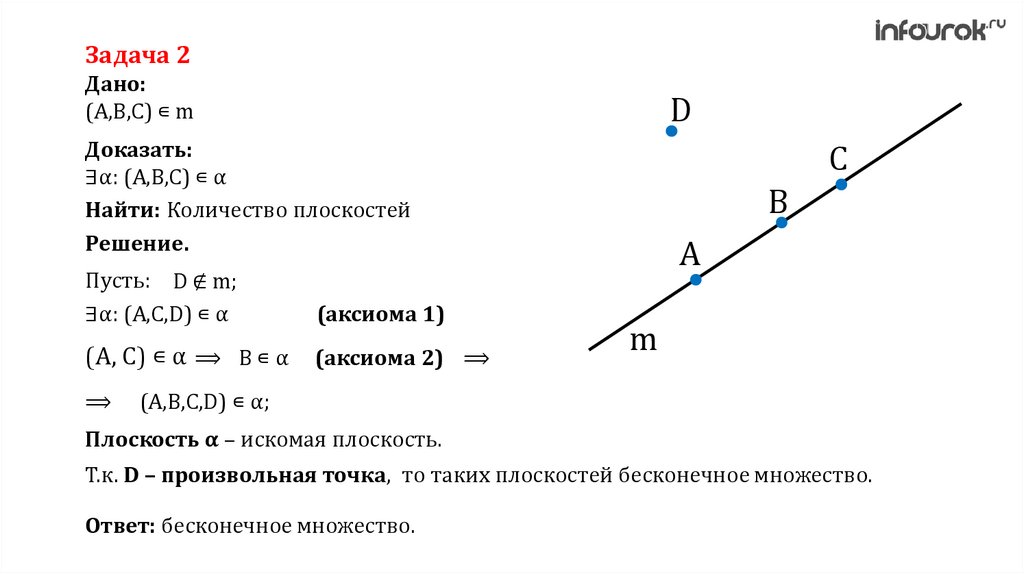
Задача 2
Дано:
(A,B,C) ∊ m
D
Доказать:
∃α: (A,B,С) ∊ α
Найти: Количество плоскостей
Решение.
Пусть: D ∉ m;
∃α: (A,C,D) ∊ α
(аксиома 1)
(A, C) ∊ α ⟹ B ∊ α
(аксиома 2) ⟹
⟹
C
B
A
m
(A,B,C,D) ∊ α;
Плоскость α – искомая плоскость.
Т.к. D – произвольная точка, то таких плоскостей бесконечное множество.
Ответ: бесконечное множество.