Похожие презентации:
Подготовка к экзамену оп математики
1.
ПОДГОТОВКА К ЭКЗАМЕНУ2.
Комплексные числаПонятие комплексного числа.
Алгебраическая форма записи
комплексного числа. Действия над
комплексными числа в алгебраической
форме записи
1
3.
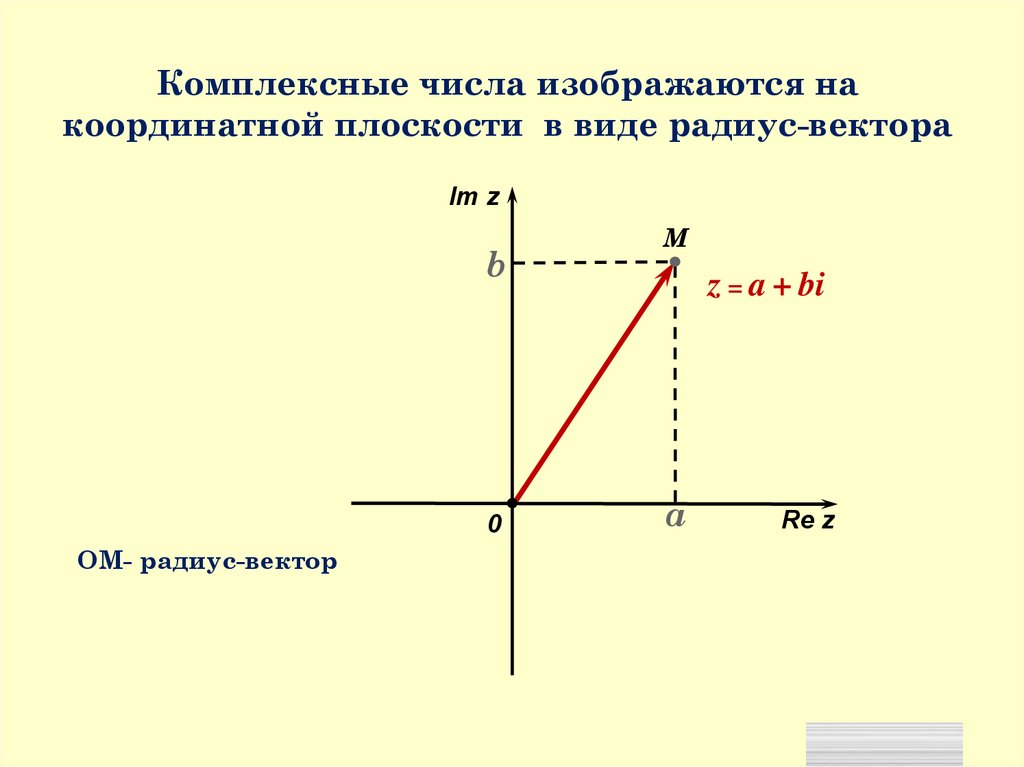
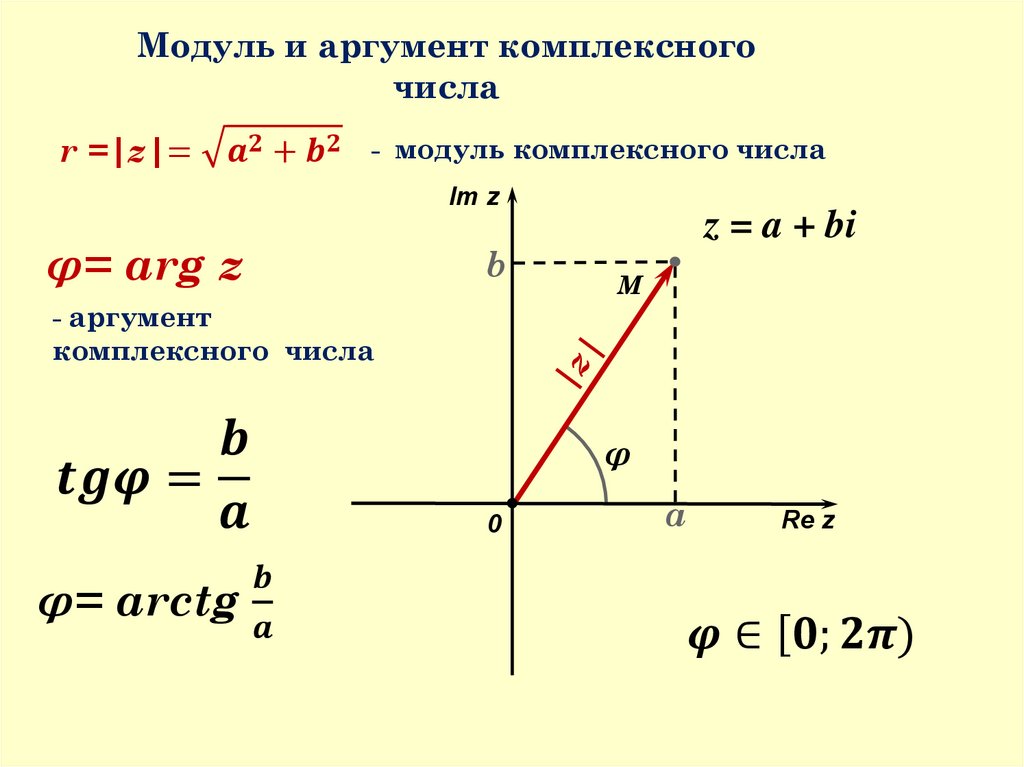
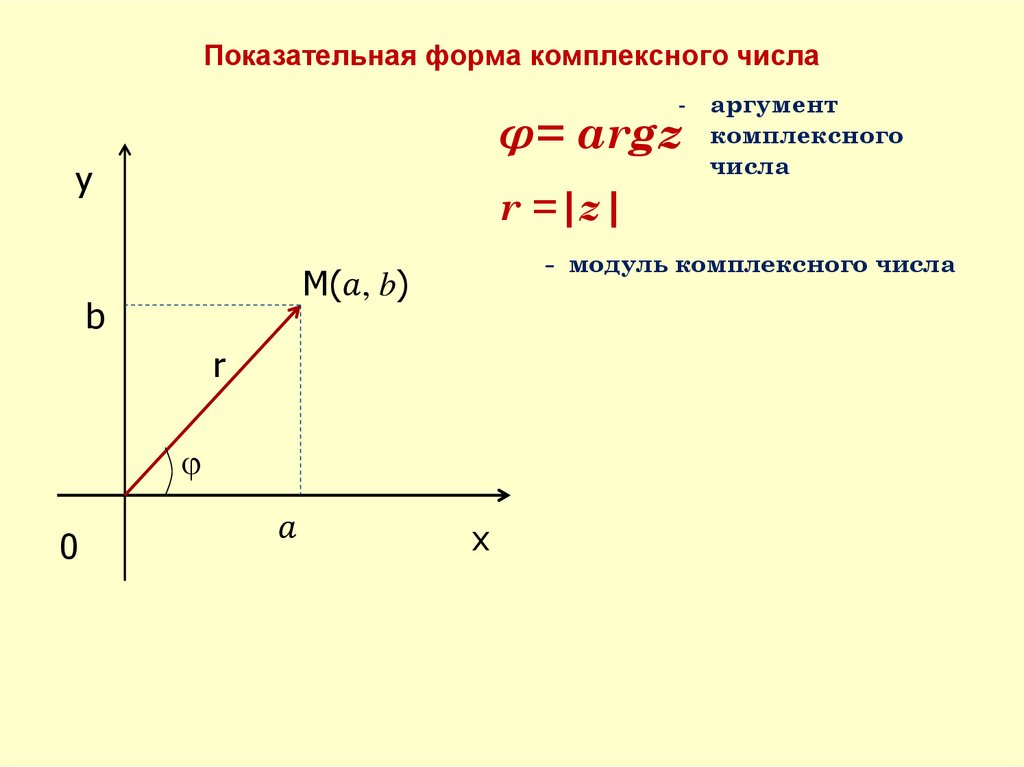
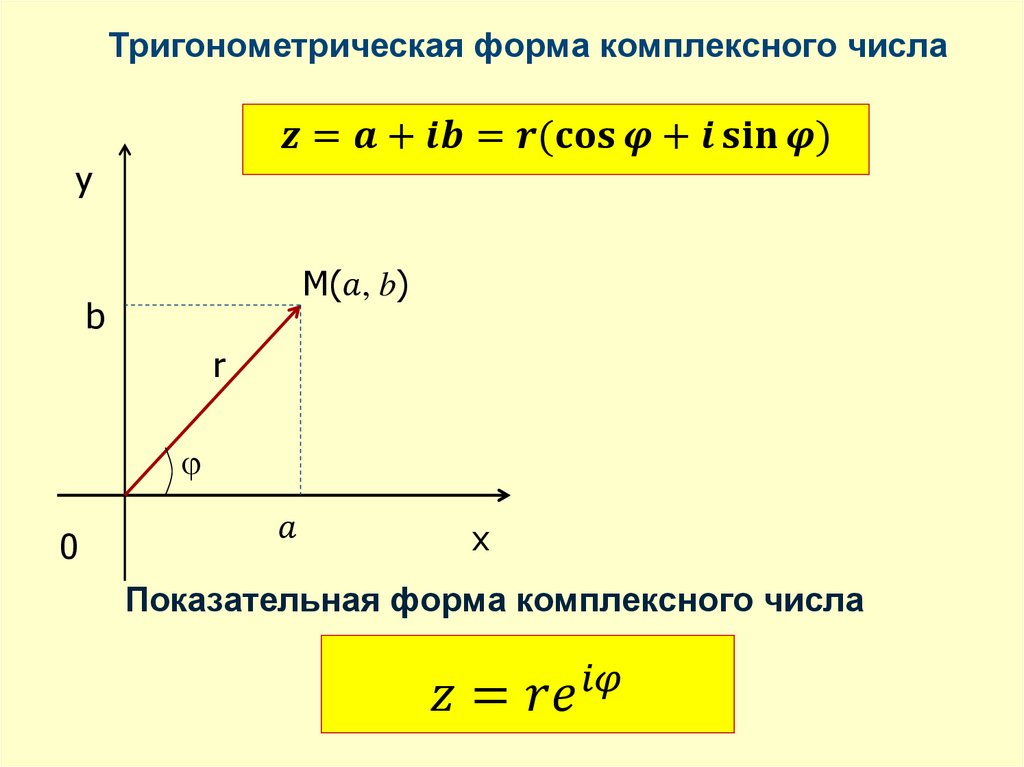
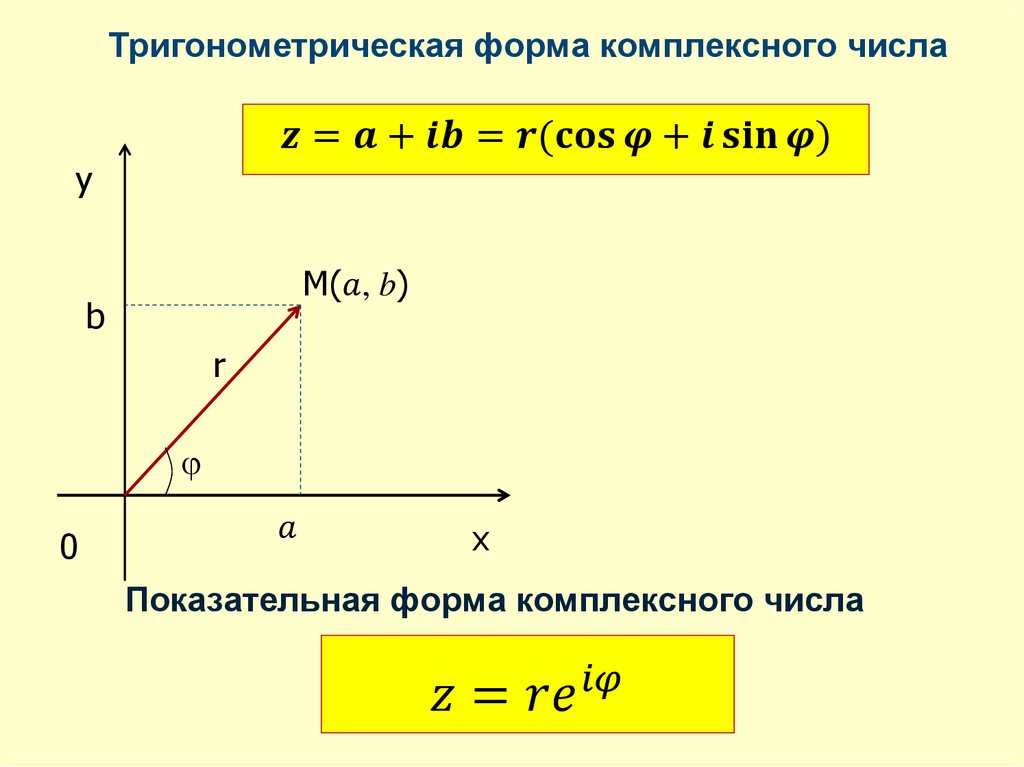
Определение:Числа вида z = a + bi, где a и b –
действительные числа, i – мнимая единица,
называются комплексными.
i2 = −1
a -действительная часть числа z
b- мнимая частью числа числа z
i- мнимая единица
z = a + bi -алгебраическая форма
записи комплексного числа.
4. Действия над комплексными числами
Сложение(a + bi) + (c + di) = (a + c) + (b + d)i
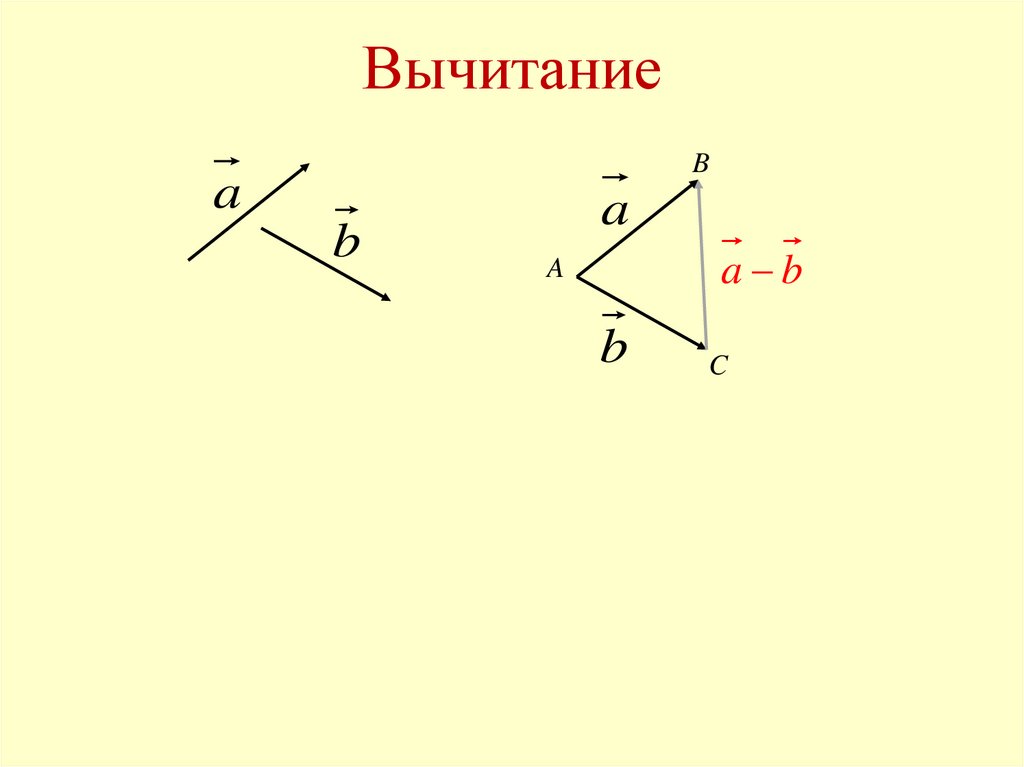
Вычитание
(a + bi) − (c + di) = (a − c) + (b − d)i
Умножение (раскрытие скобок и приведение подобных)
(a + bi) (c + di) = ac + bci + adi + bdi2 =
= (ac − bd) + (bc + ad)i
Деление (умножение числителя и знаменателя на
сопряженное знаменателю)
































































































































































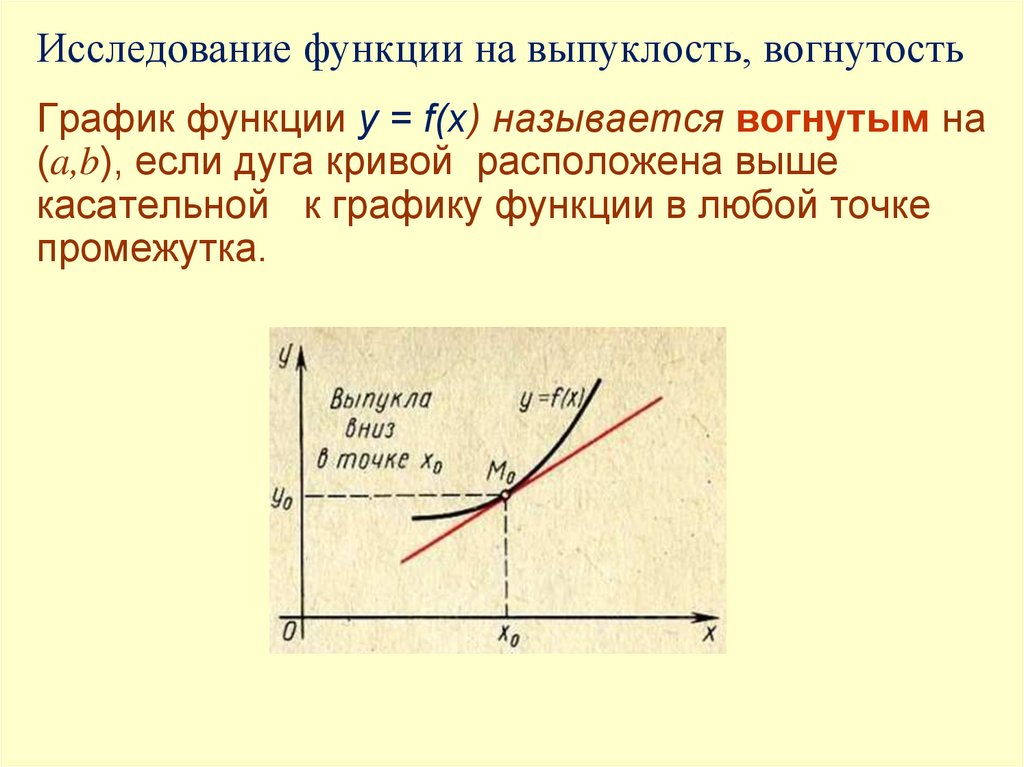
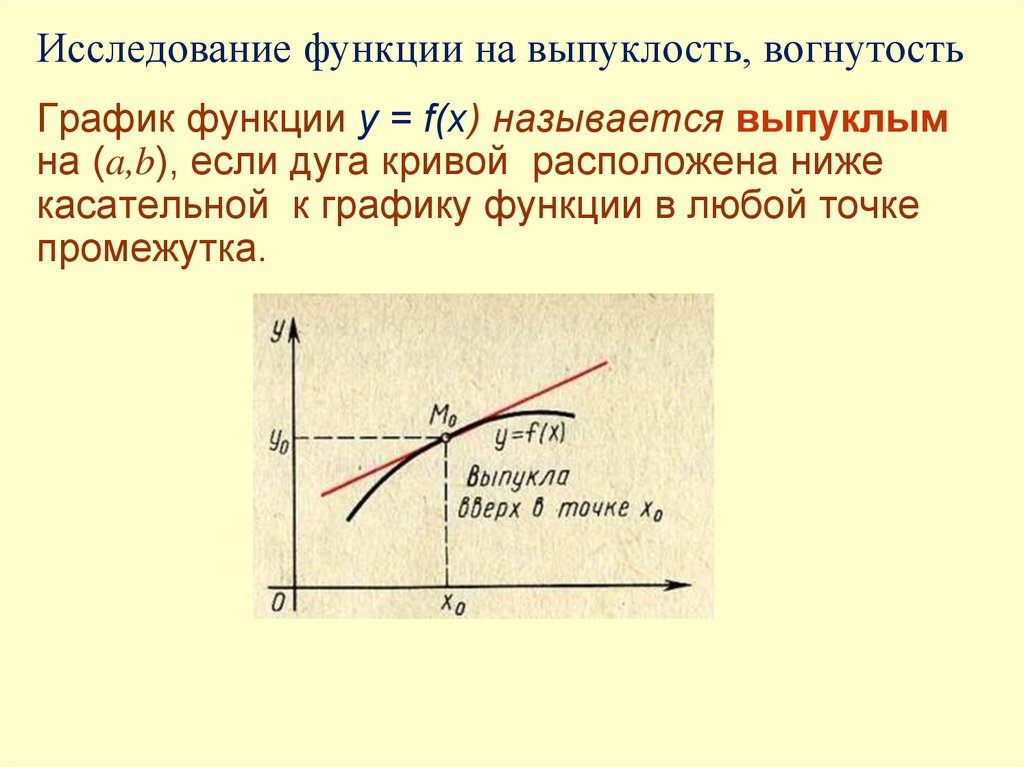

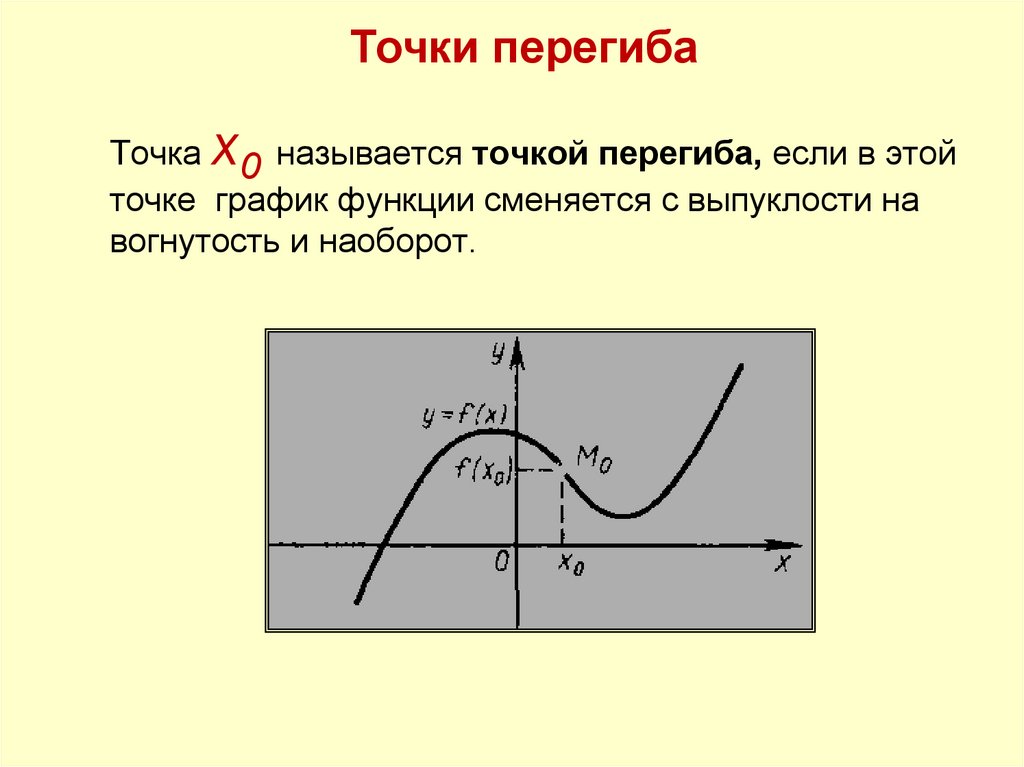




















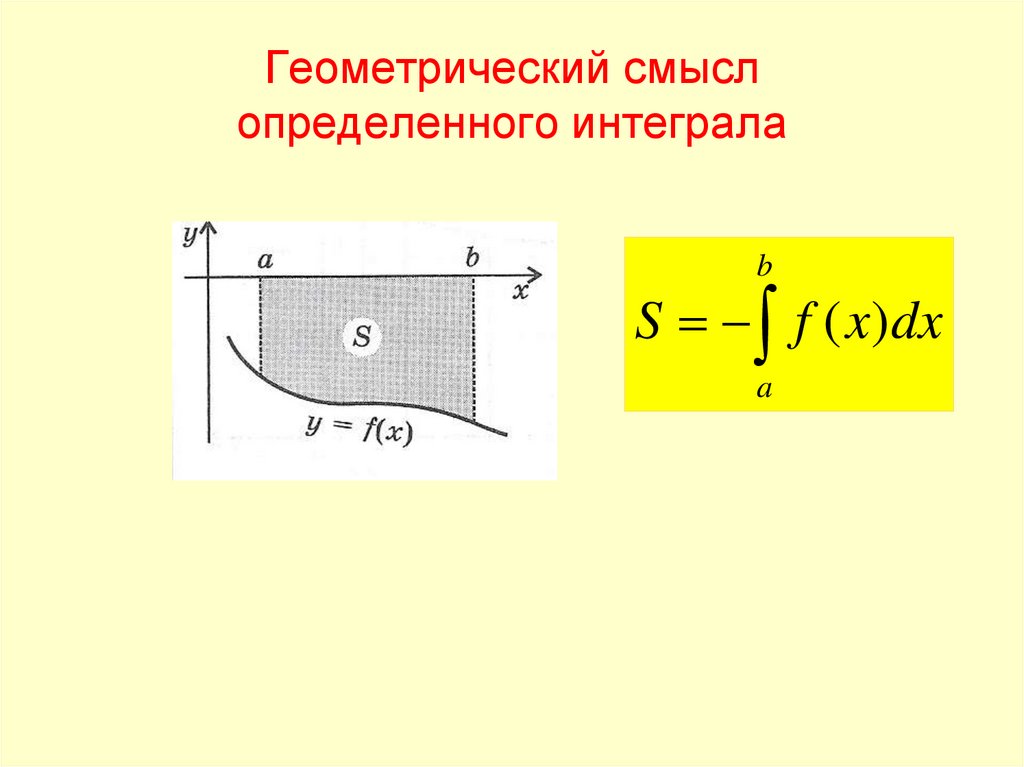
![Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где a ≠ b) называется приращение Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где a ≠ b) называется приращение](https://cf3.ppt-online.org/files3/slide/p/PyCdKYrlgvTLeot3jOQEmsw12SqBWixMaZ7u6I/slide-212.jpg)



































































 Математика
Математика








