Похожие презентации:
Второй закон термодинамики. Энтропия
1. II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К](Клаузиус)
Этоколичественный
критерий
оценки
направления
протекания
самопроизвольных
процессов (от греч. Слова «тропе» + «эн» превращение)
2. Основное содержание II начала термодинамики:
- это закономерность, позволяющаярешать вопросы о возможности
протекания процессов, их
направлении и пределе
самопроизвольного протекания.
3.
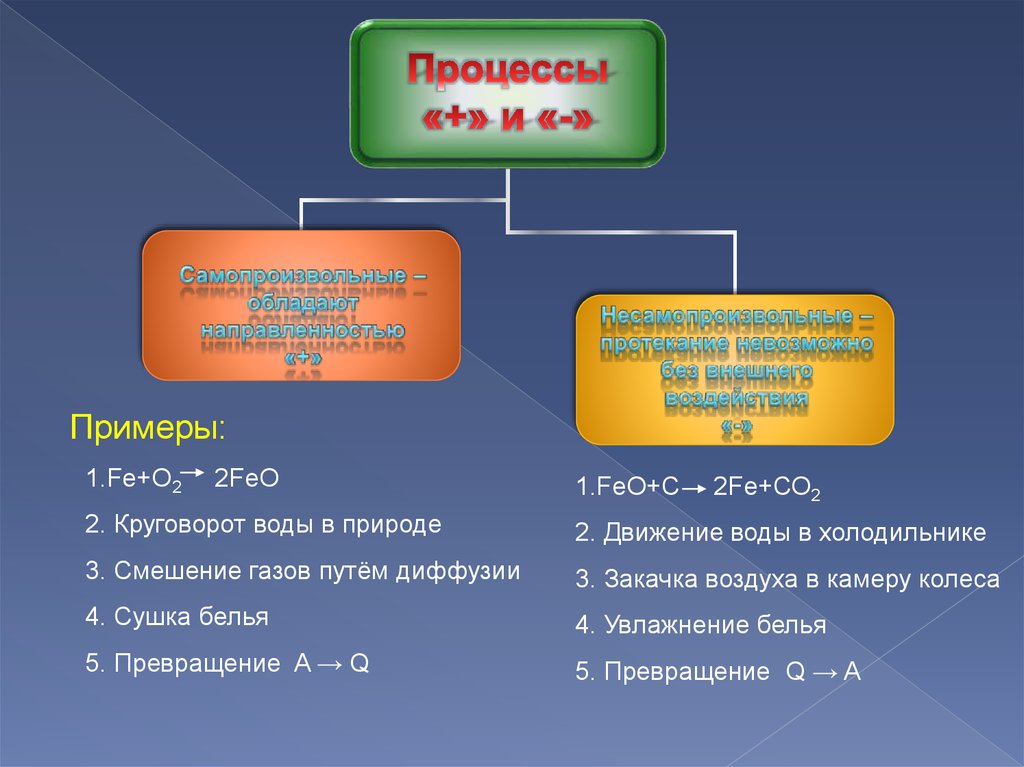
Примеры:1.Fe+O2
2FeO
1.FeO+С
2Fe+СО2
2. Круговорот воды в природе
2. Движение воды в холодильнике
3. Смешение газов путём диффузии
3. Закачка воздуха в камеру колеса
4. Сушка белья
4. Увлажнение белья
5. Превращение A → Q
5. Превращение Q → A
4.
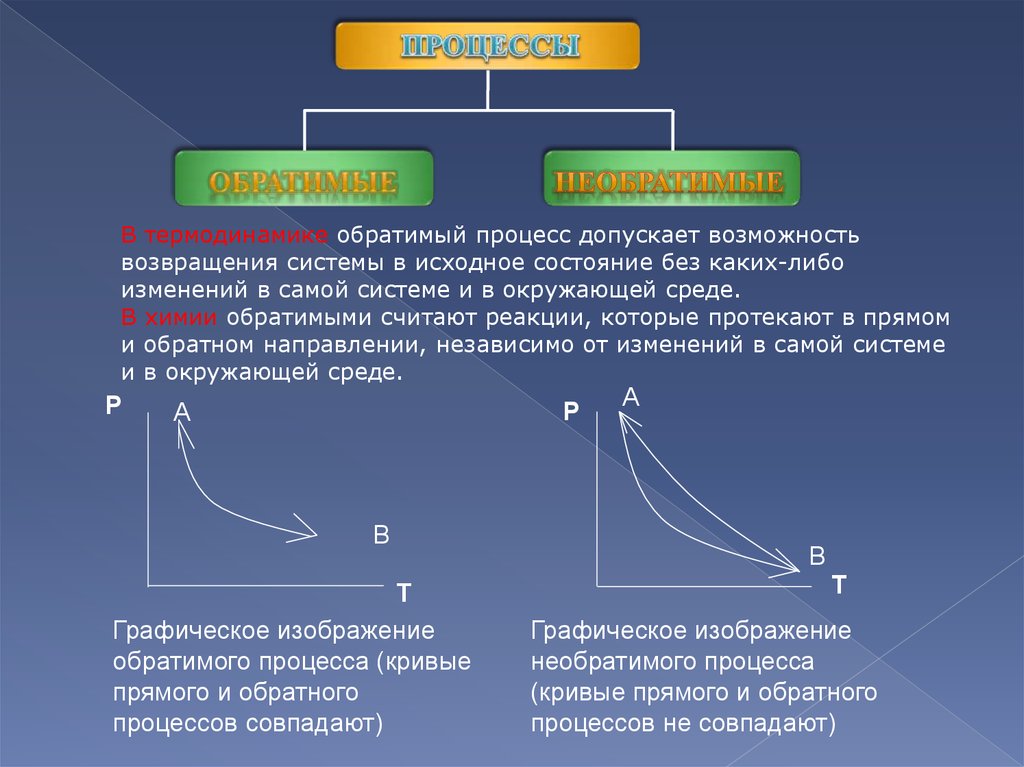
В термодинамике обратимый процесс допускает возможностьвозвращения системы в исходное состояние без каких-либо
изменений в самой системе и в окружающей среде.
В химии обратимыми считают реакции, которые протекают в прямом
и обратном направлении, независимо от изменений в самой системе
и в окружающей среде.
Р
Р
А
В
Т
Графическое изображение
обратимого процесса (кривые
прямого и обратного
процессов совпадают)
А
В
Т
Графическое изображение
необратимого процесса
(кривые прямого и обратного
процессов не совпадают)
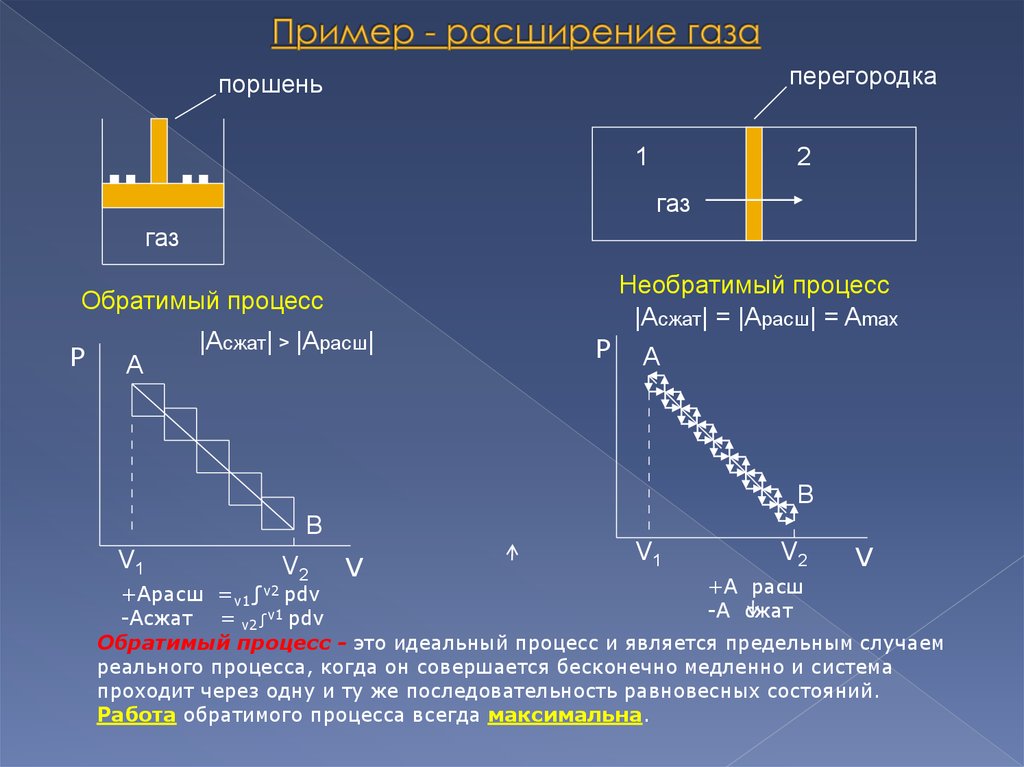
5. Пример - расширение газа
перегородкапоршень
1
2
газ
газ
Необратимый процесс
|Асжат| = |Арасш| = Amax
Обратимый процесс
P
А
|Асжат| > |Арасш|
P
А
В
В
V1
V2
V
V1
V2
V
+А расш
+Арасш =v1∫v2 pdv
-А сжат
-Асжат = v2∫v1 pdv
Обратимый процесс - это идеальный процесс и является предельным случаем
реального процесса, когда он совершается бесконечно медленно и система
проходит через одну и ту же последовательность равновесных состояний.
Работа обратимого процесса всегда максимальна.
6. Формулировки II начала термодинамики
1. «Тепло не может переходить от менее нагретого тела кболее нагретому. Оно всегда переходит от горячего к
холодному и этот переход осуществляется до тех пор пока
температуры тел не выровняются» (Клаузиус)
2. «Единственным результатом процессов не может быть только
превращение теплоты в работу, а превращение работы в
теплоту может быть» (Томсон)
3. «Невозможно построить машину, которая бы получала
работу за счет энергии источника, если температура
источника и машины одинакова» (Оствальд)
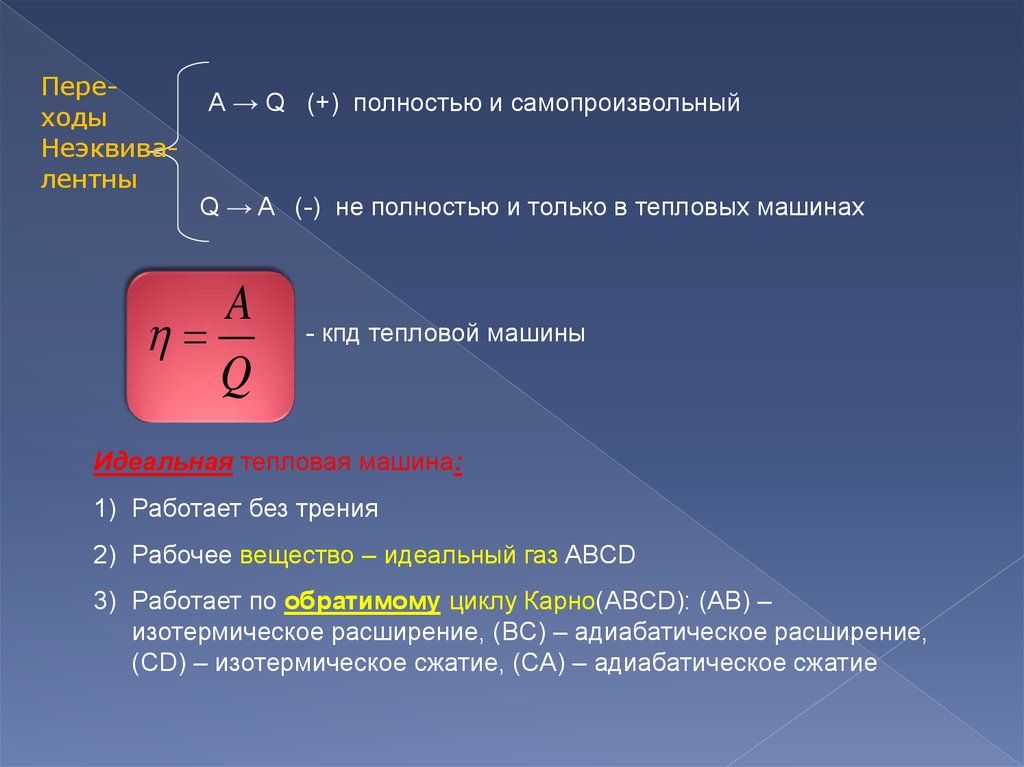
7.
ПереходыНеэквивалентны
А → Q (+) полностью и самопроизвольный
Q → A (-) не полностью и только в тепловых машинах
A
Q
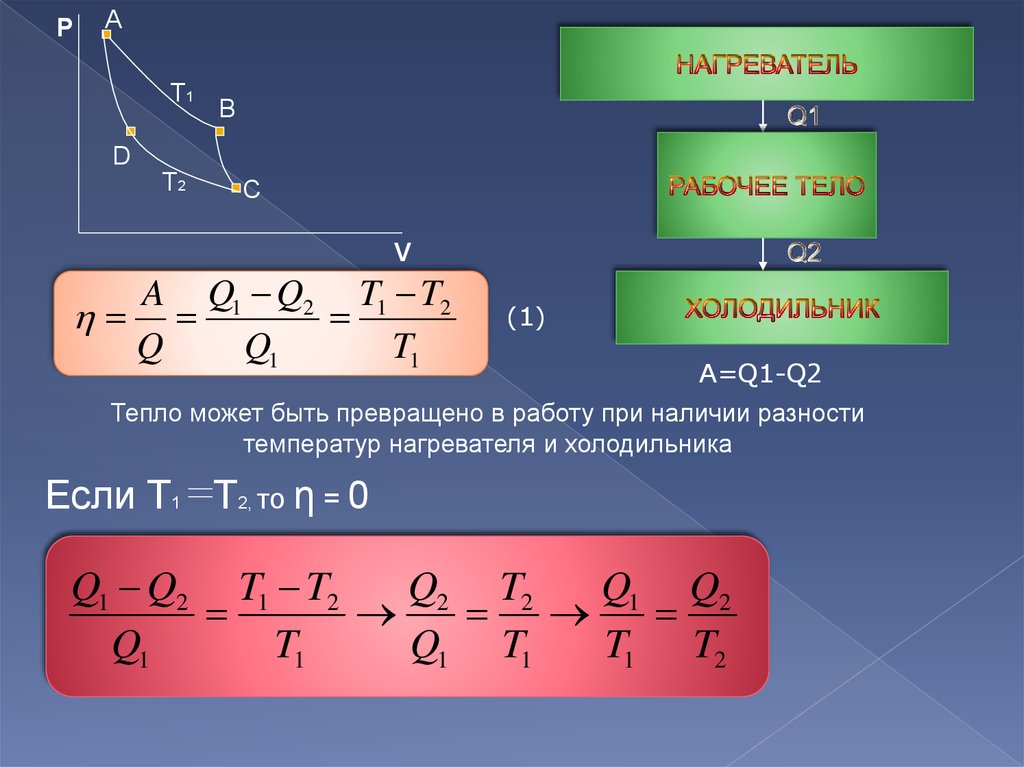
- кпд тепловой машины
Идеальная тепловая машина:
1) Работает без трения
2) Рабочее вещество – идеальный газ ABCD
3) Работает по обратимому циклу Карно(ABCD): (AB) –
изотермическое расширение, (BC) – адиабатическое расширение,
(CD) – изотермическое сжатие, (CA) – адиабатическое сжатие
8.
PA
T1
B
D
T2
C
V
A Q1 Q2 T1 T2
Q
Q1
T1
(1)
A=Q1-Q2
Тепло может быть превращено в работу при наличии разности
температур нагревателя и холодильника
Если T1 T2, то η = 0
Q1 Q2 T1 T2
Q2 T2
Q1 Q2
Q1
T1
Q1 T1
T1 T2
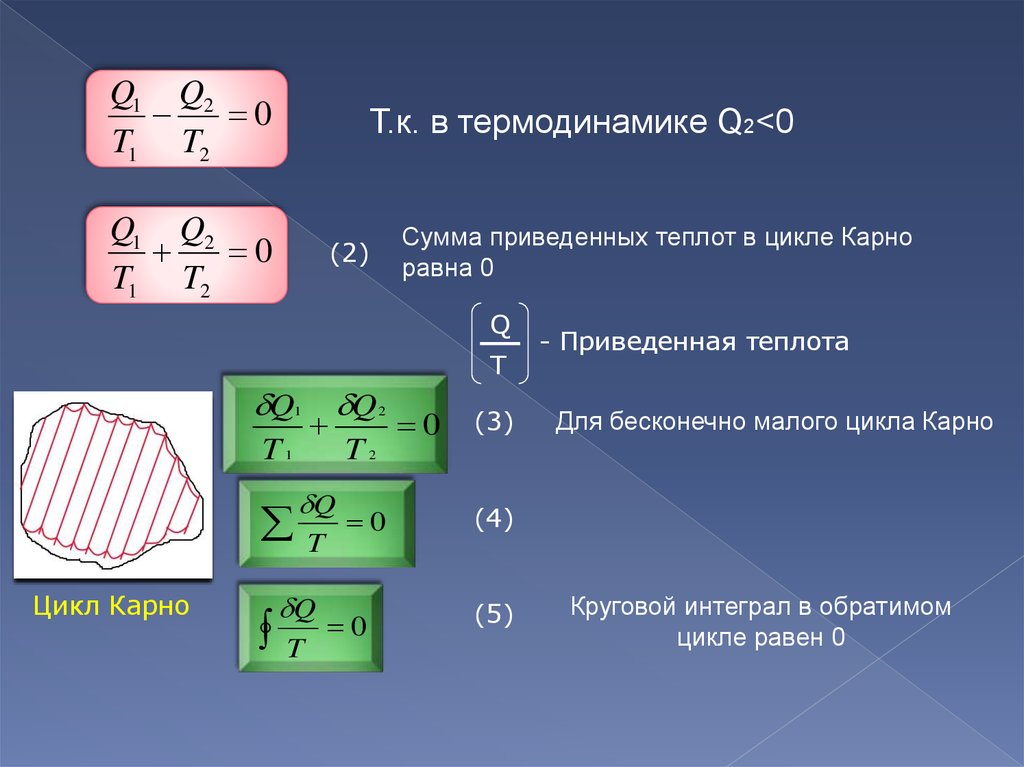
9.
Q1 Q20
T1 T2
Т.к. в термодинамике Q2<0
Q1 Q2
0
T1 T2
Сумма приведенных теплот в цикле Карно
равна 0
(2)
Q
T
Q
1
T1
Цикл Карно
Q
Q
T
Q
T
2
T2
0
0
0
(3)
- Приведенная теплота
Для бесконечно малого цикла Карно
(4)
(5)
Круговой интеграл в обратимом
цикле равен 0
10.
ТЕОРЕМА (в математике): Если интеграл по замкнутому контуру равеннулю, то подинтегральное выражение является полным дифференциалом
функции состояния. Эта функция называется «энтропией»
Q
dS
обр
T
Q
обр
T
dS
Q
Q
нео бр
Математическое выражение II начала
термодинамики для обратимого процесса
(6)
необр
T
(7)
T
т.к.
Qнеобр U A - необр.
Qобр U A max - обрат.
Математическое выражение II начала
термодинамики для необратимого процесса
dS 0 для обратимых
dS
(8) , где
T
dS 0 для необратимых
Q
Для любого процесса
11. Условия равновесия в изолированных системах
В изолированных системах : Q 0(нет теплообмена с окружающей средой)
S = Smax(∆S = 0)
S
S
dS>0
2
S
dS<0
1)dS 0; 2)d 2 S 0; 3)S S max
1-2 самопроизвольный процесс
2
1
3
Ход процесса
состояние равновесия
2-3 несамопроизвольный процесс
(9)
12.
Реальные , в том числе наблюдаемые в природе,самопроизвольные процессы-необратимые,
протекающие в направлении увеличения энтропии
системы. Они заканчиваются при достижении
равновесия, когда энтропия достигает постоянного и
максимального значения
Энтропия – это критерий для изолированных систем
Подавляющее большинство реальных систем, в том
числе и биосистем, являются открытыми и
охарактеризовать протекающие в них процессы с
помощью энтропии невозможно.
Статистический Характер II начала термодинамики
I начало – абсолютный закон (не зависит от числа частиц в системе)
II начало – вероятностный закон (зависит от числа частиц, т.е. имеет
статистический характер).
13. Энтропия и термодинамическая вероятность
S – экстенсивный параметрS K Б ln W (10)
- Уравнение Больцмана
R
8,314
23
KБ
1
,
38
10
N A 6,02 10 23
W 1 S 0
W
S
W – термодинамическая
вероятность – это число
микросостояний которыми может
быть осуществлено данное
макросостояние системы(Wmin=1)
N!
W
N1!N 2!...N n !
Пример:
n=10 книг(4 полки); W1=1260(N-общее число перестановок;
Ni=число перестановок каждой книги)
n=106молекул; W2=1260◦105=1,26 ◦ 108
14. Способы расчета изменения энтропии (для обратимых процессов)
1) Изотермический процесс (Т=const)Q du pdV
(1)
I начало термодинамики
Q TdS
(2)
II начало термодинамики
TdS du pdV
(3)
Объединенное уравнение
TdS pdV
dS
P
dV
T
dS
R
dV
V
S R ln
P1
P2
u f (T ) u const ; du 0
pV RT
(4)
S R ln
V2
V1
(5)
15. Фазовые переходы (T=const)
dSQ
T
S
H ф . п .
(6)
Tф.п.
T2
2) Изобарный процесс (P=const)
Q p C p dT
T2
S
Cp
T dT
dS C p
dT
T
S C p ln
T2
T1
2)C p f (T )
S a ln
T2
b(T2 T1 ) ...
T1
Для 1моля
T1
T
dT
(10)
T2
S v
(7)
T1
1)C p const
S v
Cp
3) Изохорный процесс (V=const)
Q TdS
TdS C p dT
- молей
(8)
Cv
T 1 T dT (11)
4) Изобарно – изотермический
(P=const; T=const )
ΔS ΔS p ΔST
(12)
5) Изохорно – изотермический
(V=const; T=const )
(9)
S SV ST
(13)
 II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К](Клаузиус)](https://cf.ppt-online.org/files/slide/i/IFf10cewhokWR9q3MzsnHQ76ASbyX2uN8mxiBd/slide-0.jpg)








 Физика
Физика
![II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К] (Клаузиус) II Закон термодинамики. Энтропия “S”- термодинамическая функция состояния [Дж/моль К] (Клаузиус)](https://cf3.ppt-online.org/files3/thumb/s/shTr2KkzXY6Gb1DP9c5MVIEZmtq4nJoUfBC7Ll.jpg)







