Проецирование точки

1. ПРОЕЦИРОВАНИЕ ТОЧКИ

Геометрический объект любой сложности можно рассматривать как
геометрическое место точек, по взаимному расположению, которых можно
составить представление об объекте, а по расположению их относительно системы
координат можно судить о положении его в пространстве.
Точка *- одно из основных понятий геометрии.
МЕТОД МОНЖА
Если информацию о расстоянии точки относительно плоскости проекции
дать с помощью второй проекции точки, построенной на второй плоскости проекций,
то получаем чертеж который называют двухкартинным или комплексным.
Принцип образования такого чертежа состоит в том, что фигура проецируется
ортогонально на две взаимно перпендикулярные плоскости проекций, которые затем
соответствующим образом совмещают с плоскостью чертежа. Одна из плоскостей
проекций П1 располагается горизонтально и называется горизонтальной плоскостью
проекций. Плоскость П2 располагается вертикально перед наблюдателем и называется
фронтальной плоскостью проекций. Прямую пересечения плоскостей проекций
называют осью проекций.

2.

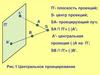
ПРОЕЦИРОВАНИЕ ТОЧКИ
Двухкартинный комплексный чертёж точки
z
П2
А”
А
П1
Аz
О
Ах
x
A’(Ax;Ay)
А”(Ax;Az)
A’
Аy
y

3.

ПРОЕЦИРОВАНИЕ ТОЧКИ
Двухкартинный комплексный чертёж точки
z
П2
A”
Аz
Ах
О
x
A’
Аy
П1
y

4.

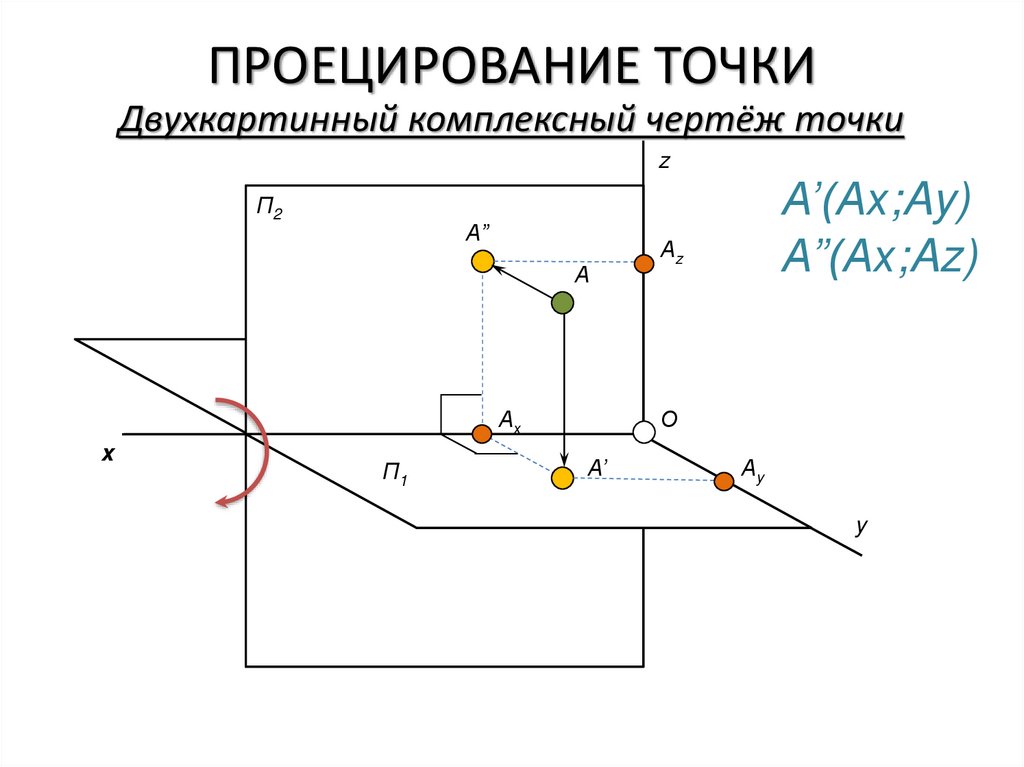
ПРОЕЦИРОВАНИЕ ТОЧКИ
Двухкартинный комплексный чертёж точки
B
z
П2
z
П2
B”
B”
C’
B’
C’
B’
Dх
Cх
x
Сх
О
x
Bх
C
D’
П1
C”
D”
Dх
О
Bх
y
Dy Dz
D
П1
C”
D’=D”
y

5.

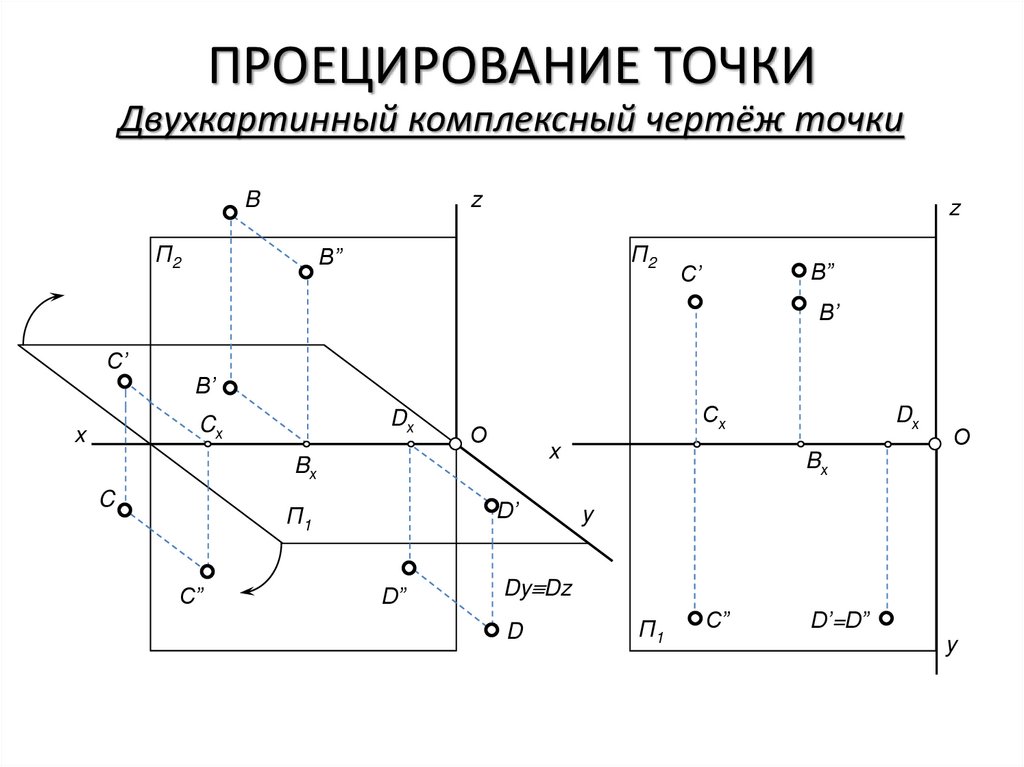
ПРОЕЦИРОВАНИЕ ТОЧКИ
Трёхкартинный комплексный чертёж точки
z
П2
П3
О
x
П1
y

6.

ПРОЕЦИРОВАНИЕ ТОЧКИ
Трёхкартинный комплексный чертёж точки
V,VI,VII,VIII
z
П2
A”
АZ
А
II
A’”
I
АX
x
III
П3
IV
О
П1
A’
АY
y

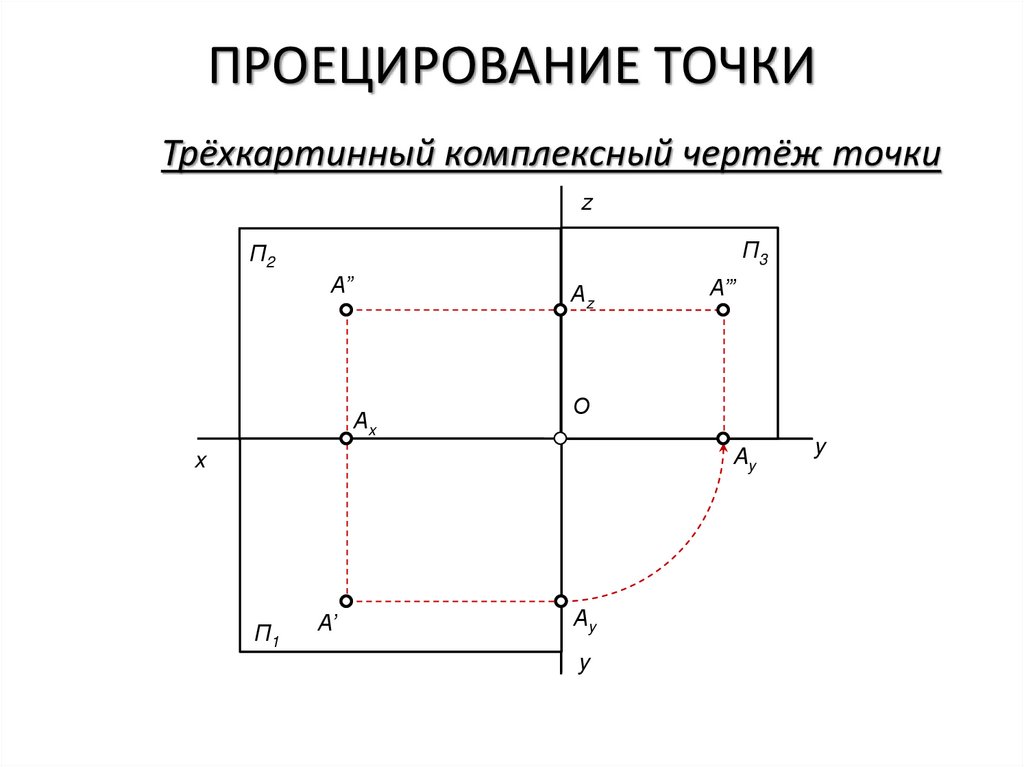
7.

ПРОЕЦИРОВАНИЕ ТОЧКИ
Трёхкартинный комплексный чертёж точки
z
П3
П2
A”
Аz
Аx
A’”
П3
О
Ay
x
П1
A’
Аy
y
y

8.

ПРОЕЦИРОВАНИЕ ТОЧКИ
В результате указанного совмещения плоскостей
проекций получим трехкартинный комплексный чертеж ,
который будет называться эпюром.
Эпюр-чертёж на котором все три плоскости
проекций совмещены с плоскостью чертежа, при этом за
плоскость чертежа принимается фронтальная плоскость
проекций
Введенная система трех плоскостей проекций П1,
П2 и П3 разделяет все пространство на восемь частей,
называемых октантами.

9.

ПРОЕЦИРОВАНИЕ ТОЧКИ
VI
II
П2
V
П3
I
III
VII
П1
IV
VIII