Центральное проецирование. Лекция №1

1.

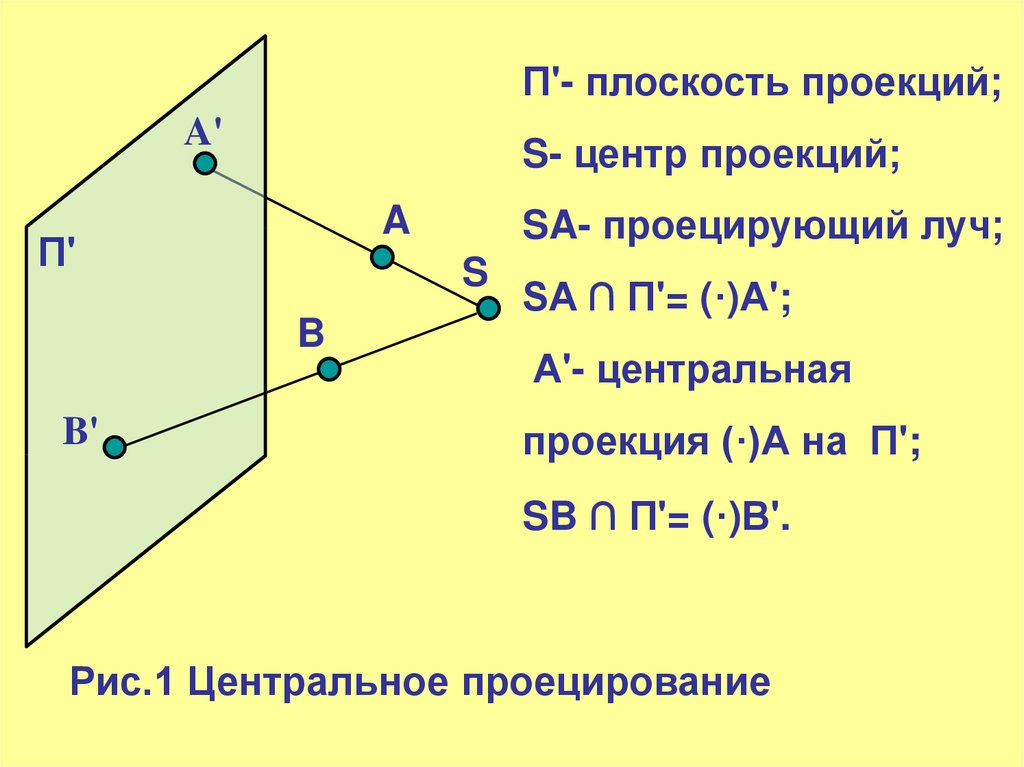
П'- плоскость проекций;
A'
S- центр проекций;
П'
S
B
B'
SA- проецирующий луч;
A
SA ∩ П'= (·)А';
А'- центральная
проекция (·)А на П';
SB ∩ П'= (·)В'.
Рис.1 Центральное проецирование

2.

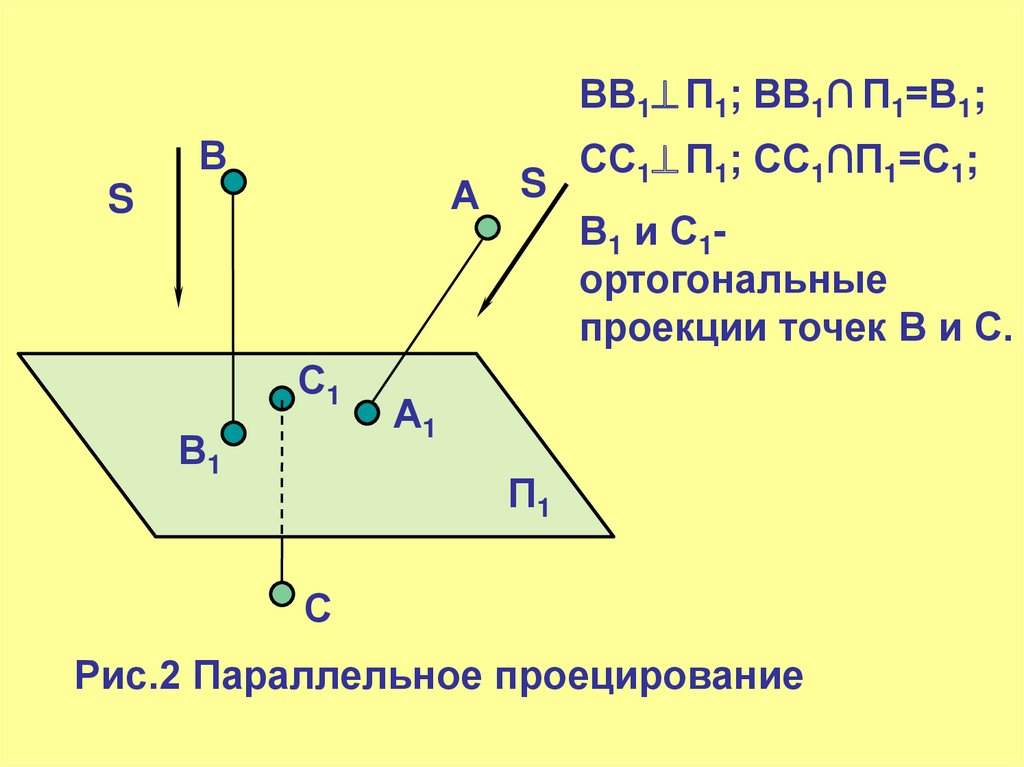
ВВ1 П1; ВВ1∩ П1=В1;
В
А
S
С1
В1
S
СС1 П1; СС1∩П1=С1;
В1 и С1ортогональные
проекции точек В и С.
А1
П1
С
Рис.2 Параллельное проецирование

3. Свойства параллельного проецирования

Проекцией точки является точка.
Проекцией прямой линии является
прямая.
Проекцией точки, лежащей на
прямой, является точка, лежащая
на проекции данной прямой.
Проекция фигуры не меняется при
параллельном переносе плоских
проекций.

4.

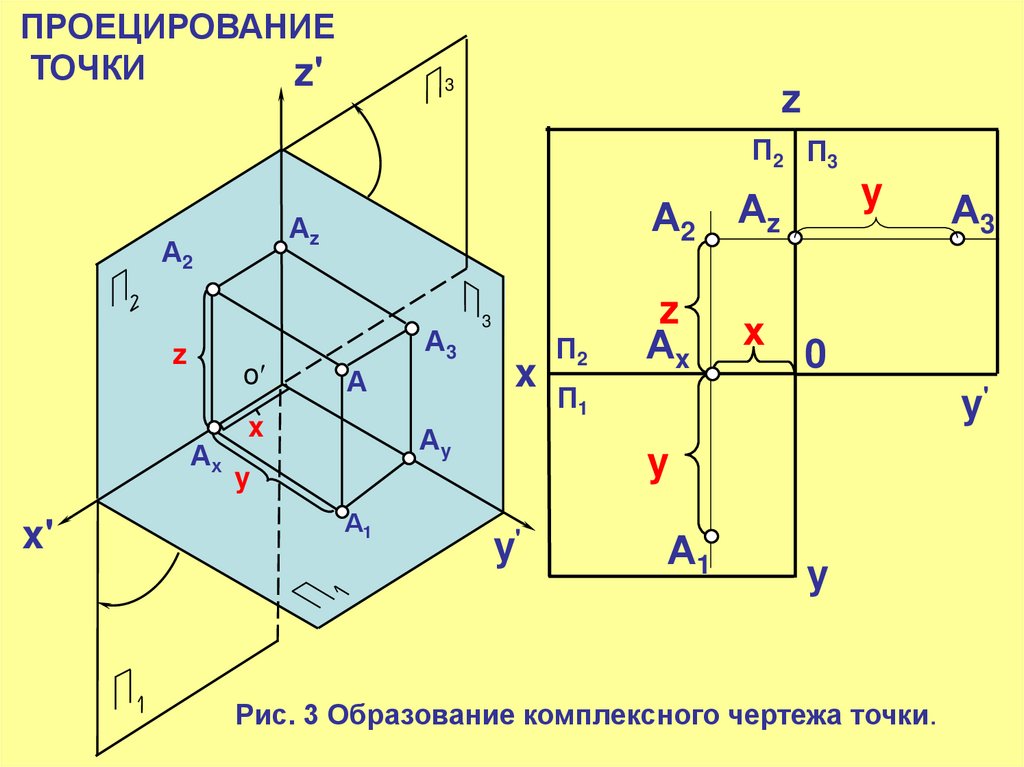
ПРОЕЦИРОВАНИЕ
ТОЧКИ
z'
3
z
Π2 Π3
Аz
А2
А3
z
o
Ах
x'
А
x
3
x
Аy
z
Аx
х
y
y'
А3
0
Π1
y'
y
y
А1
Π2
А2
Аz
А1
y
Рис. 3 Образование комплексного чертежа точки.

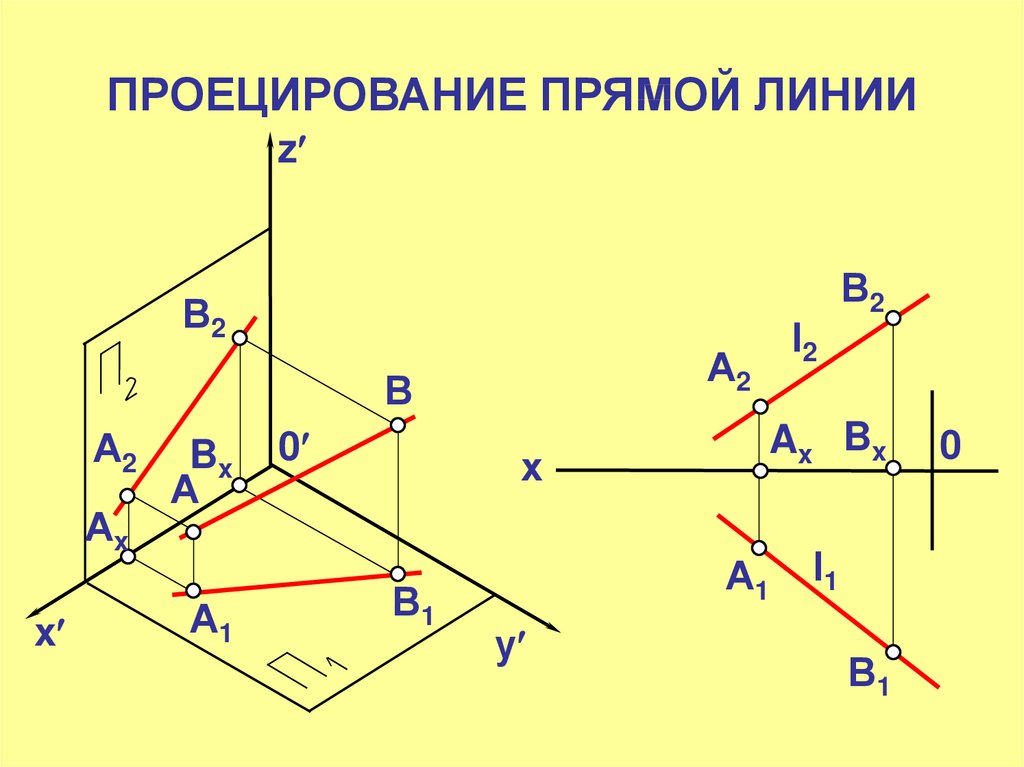
5. ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ

z
В2
В2
А2
В
А2
Аx
х
Bx
А
А1
0
х
В1
l2
Ax Bx
А1
у
l1
В1
0

6. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
z
A2 h2
В2
А2
x'
А
А1
o'
В
В1
B2 A3 h3 B3
o
x
A1
y'
β
h1
γ
В1
у
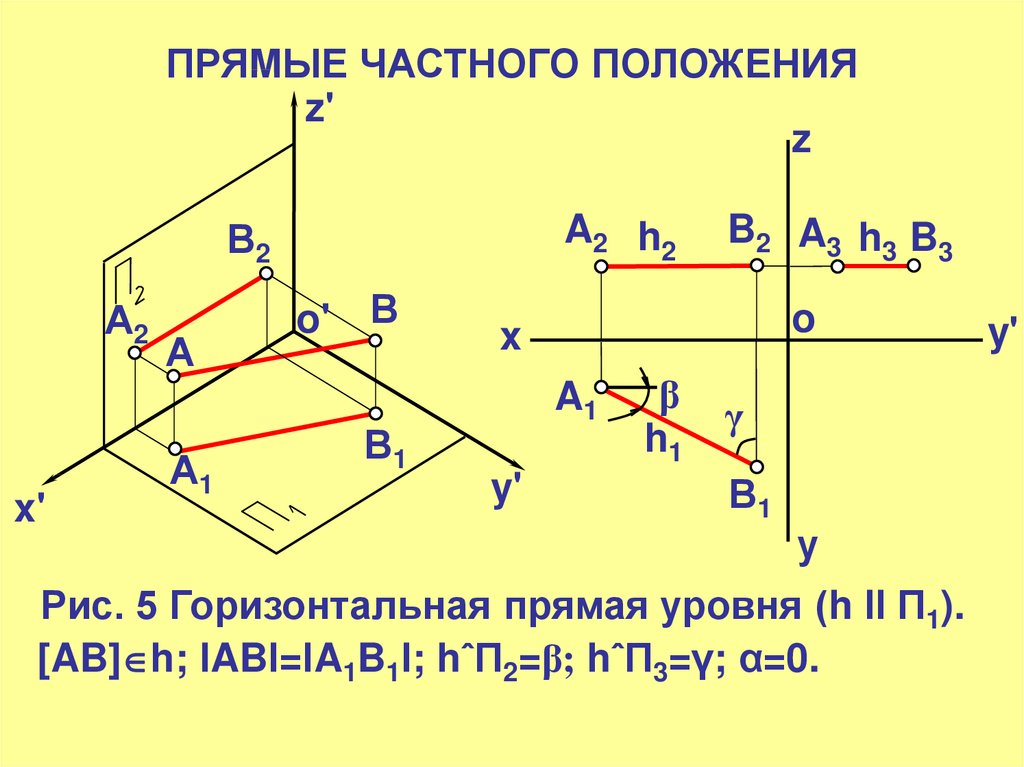
Рис. 5 Горизонтальная прямая уровня (h ll П1).
[AB] h; lABl=lA1B1l; hˆП2=β; hˆП3=γ; α=0.
y'

7. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
z
D2
o'
C2
C
x'
D
C1
C2
D3
D2
f
α 2
γ
f3
o
x
C3
f1
D1
C1
y'
D1
у
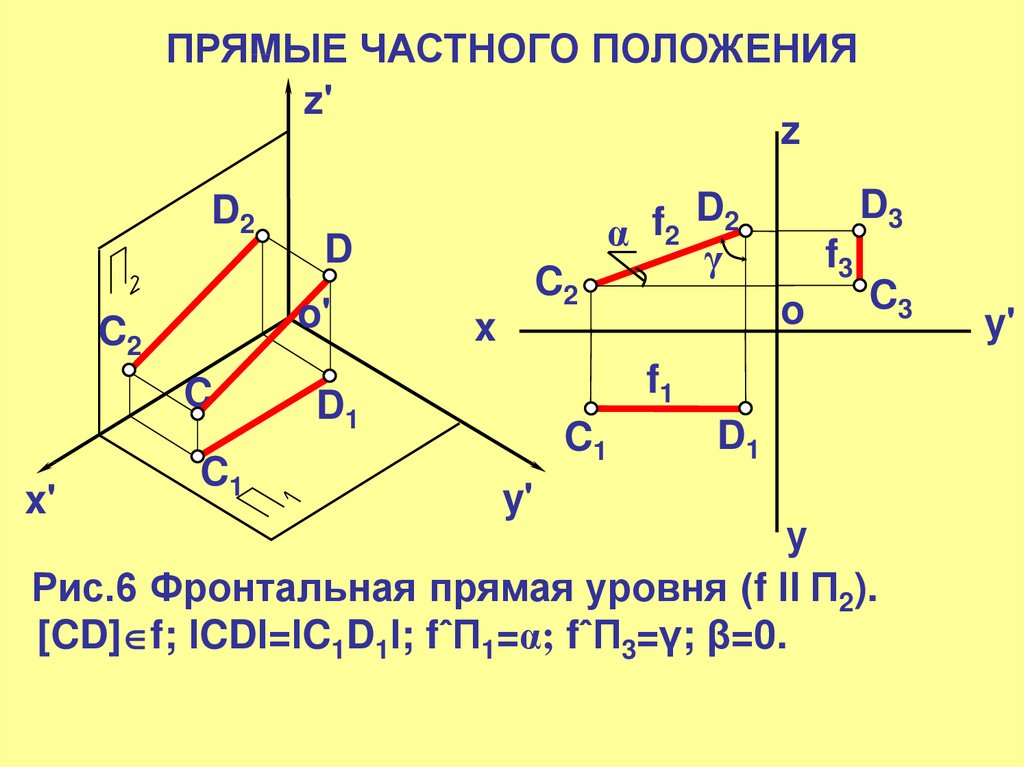
Рис.6 Фронтальная прямая уровня (f ll П2).
[CD] f; lCDl=lC1D1l; fˆП1=α; fˆП3=γ; β=0.
y'

8. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
z
E3
E3
E2
E2
p3
E
p
2
β α F3
o'
F2
o
F2
y'
F3
x
E1
F
E1
p1
х'
F1
у' F1
у
3
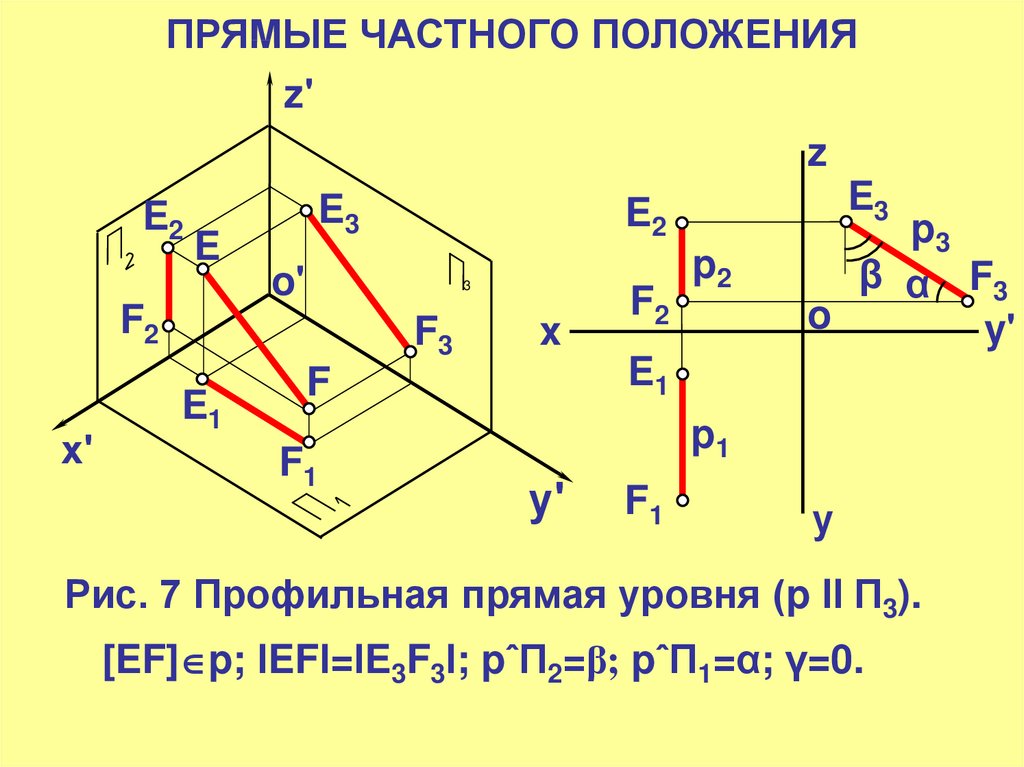
Рис. 7 Профильная прямая уровня (p ll П3).
[EF] p; lEFl=lE3F3l; pˆП2=β; pˆП1=α; γ=0.

9. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
A2
A2
B2
x'
A
i2
B2
B o'
A1≡B1
y' i1≡A
i1≡A
1≡B
1≡(B
1) 1
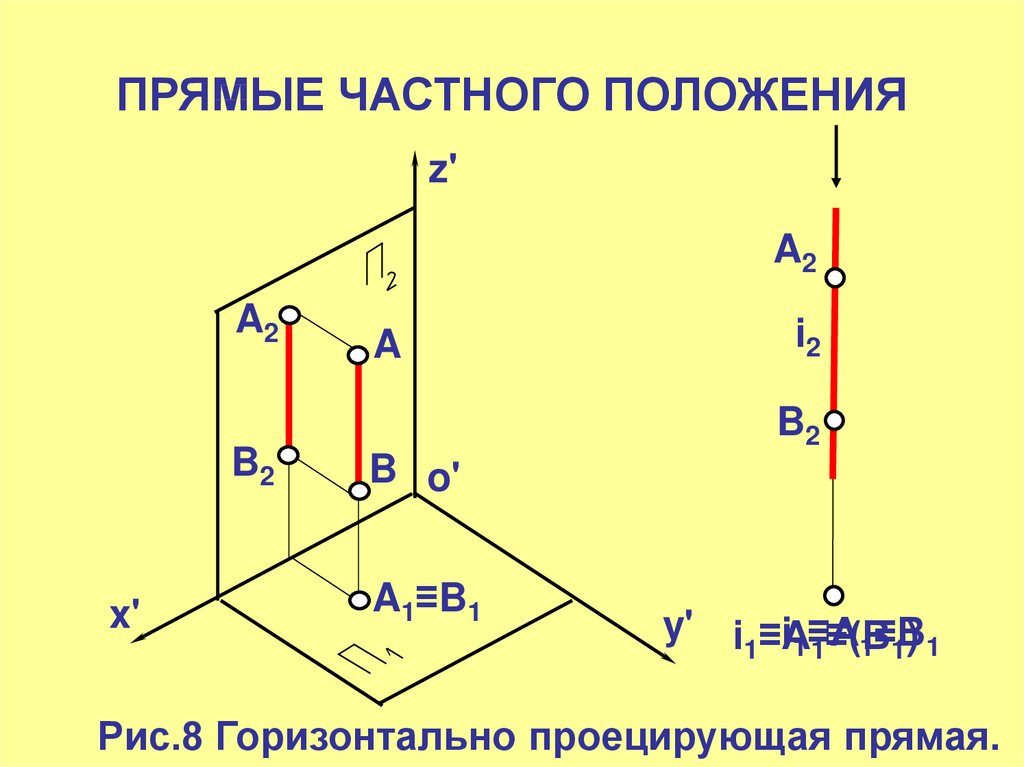
Рис.8 Горизонтально проецирующая прямая.

10. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
ii22≡A
≡A22≡(B
≡B22)
A2=B2
B
A
B1
o'
i1
x'
B1
A1
y'
A1
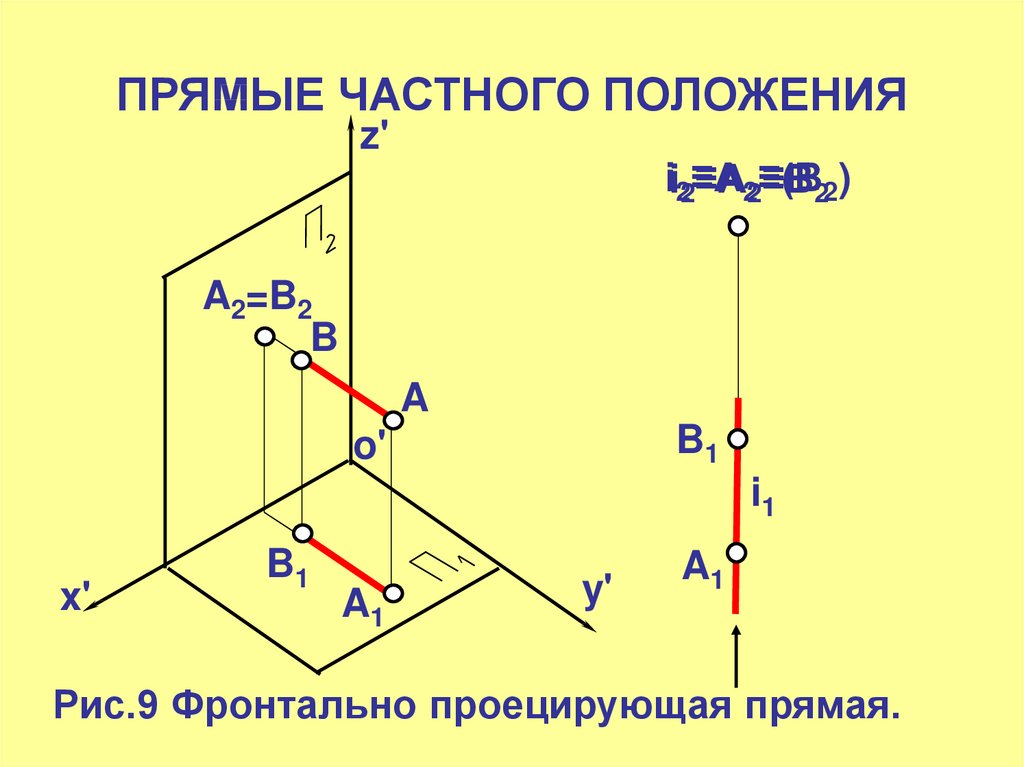
Рис.9 Фронтально проецирующая прямая.

11. ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

z'
A2
A2
A
x'
B
A1
ii33≡A
≡A33≡B
≡(B3 3)
i2
A3=B3
B2
B2
o'
B1
y'
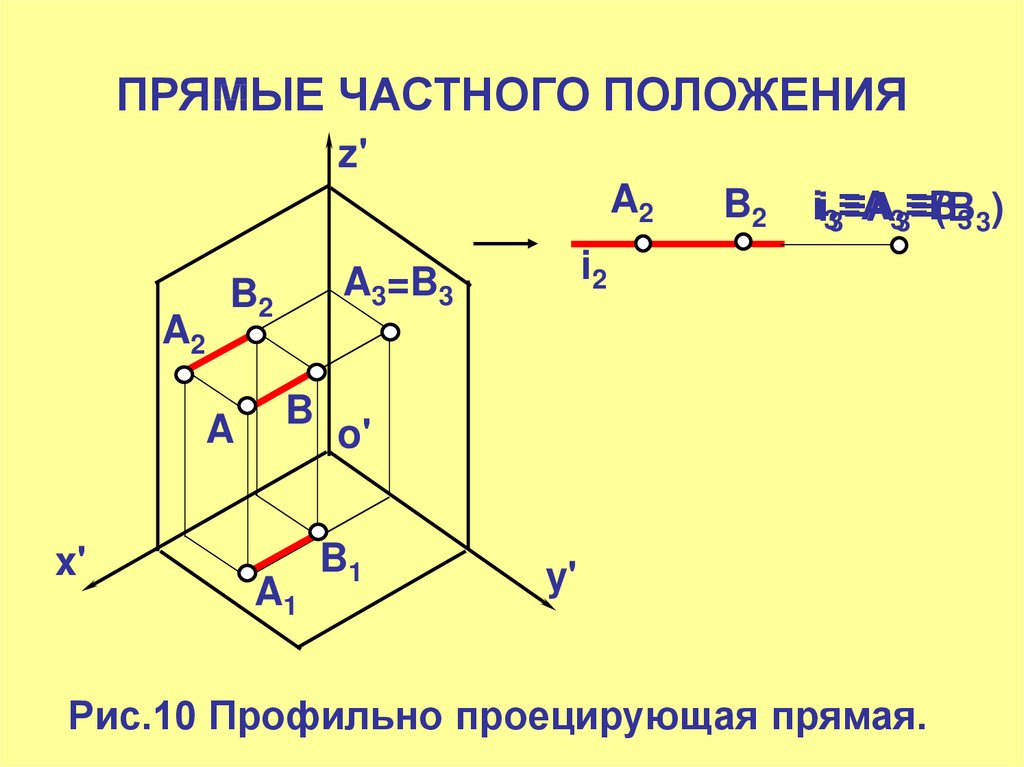
Рис.10 Профильно проецирующая прямая.

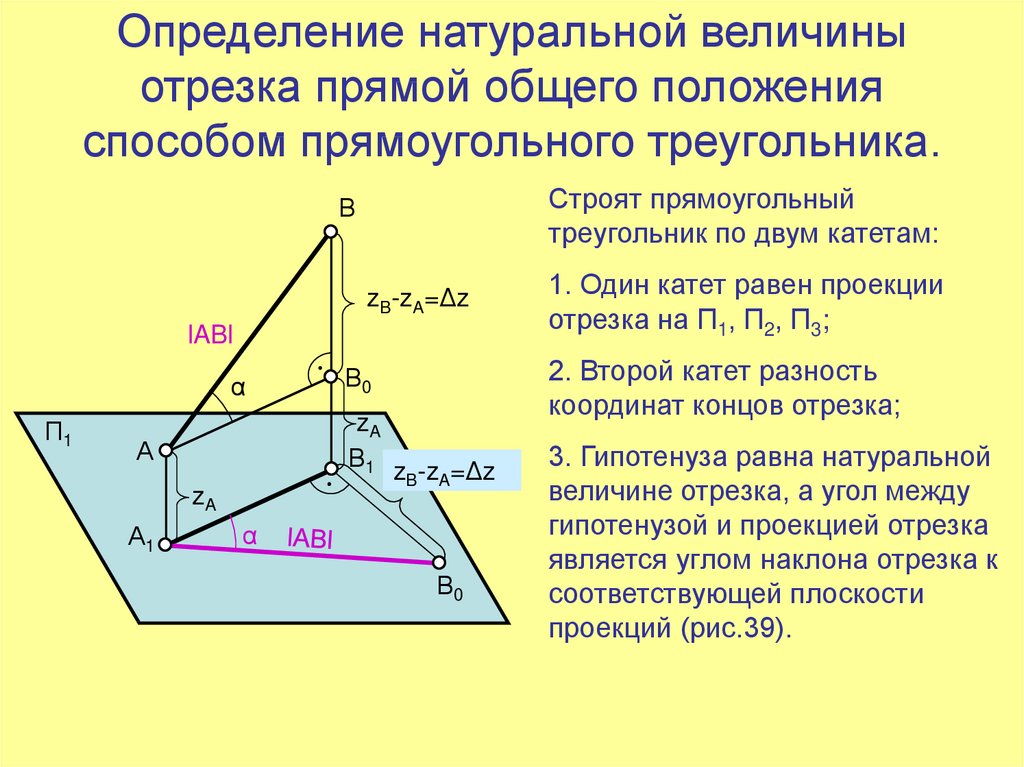
12. Определение натуральной величины отрезка прямой общего положения способом прямоугольного треугольника.

Строят прямоугольный
треугольник по двум катетам:
В
zB-zA=Δz
lABl
α
П1
А
zA
А1
2. Второй катет разность
координат концов отрезка;
В0
zA
В1
1. Один катет равен проекции
отрезка на П1, П2, П3;
zB-zA=Δz
α
В0
3. Гипотенуза равна натуральной
величине отрезка, а угол между
гипотенузой и проекцией отрезка
является углом наклона отрезка к
соответствующей плоскости
проекций (рис.39).

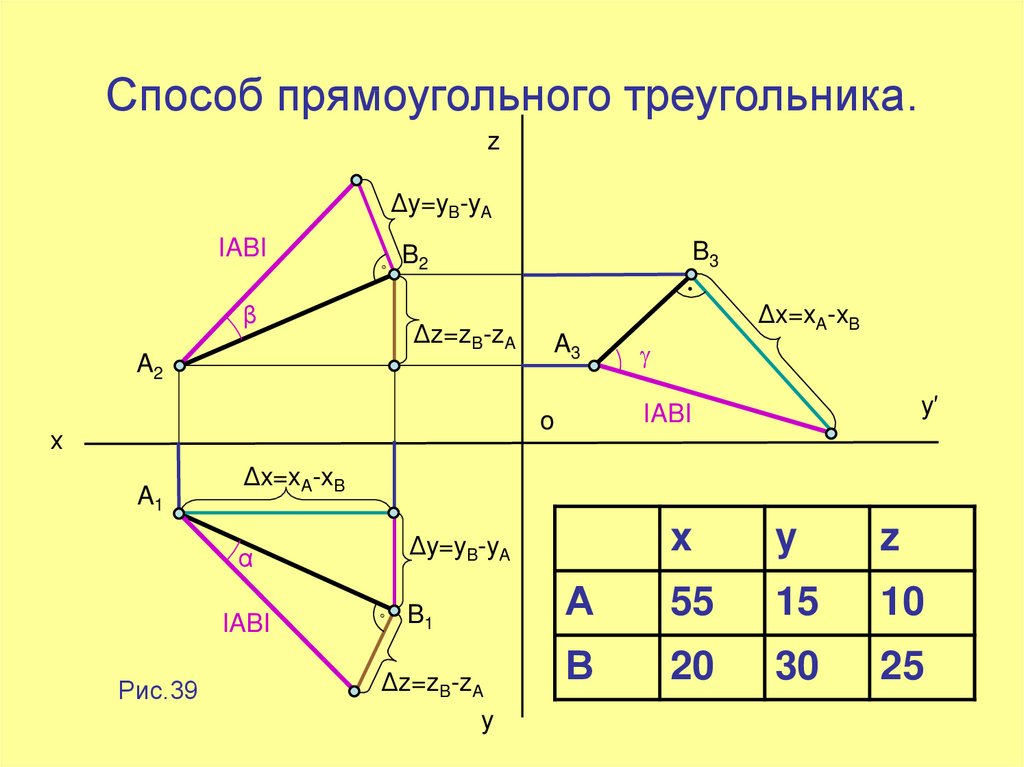
13. Способ прямоугольного треугольника.

z
Δy=yB-yA
IABI
β
B3
B2
Δz=zB-zA
A2
Δx=xA-xB
A3
A1
Δx=xA-xB
α
IABI
Рис.39
y′
IABI
o
х
x
y
z
А
55
15
10
В
20
30
25
Δy=yB-yA
B1
Δz=zB-zA
y

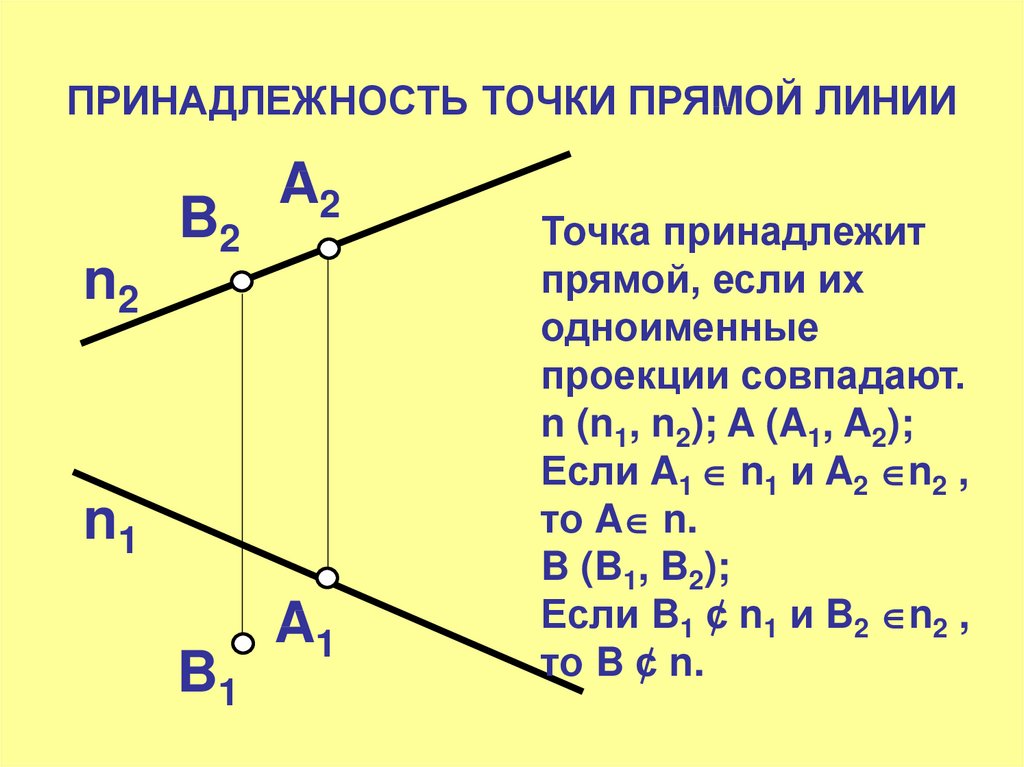
14. ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ ЛИНИИ

n2
B2
A2
n1
B1
A1
Точка принадлежит
прямой, если их
одноименные
проекции совпадают.
n (n1, n2); A (A1, A2);
Если A1 n1 и A2 n2 ,
то A n.
B (B1, B2);
Если B1 ¢ n1 и B2 n2 ,
то B ¢ n.

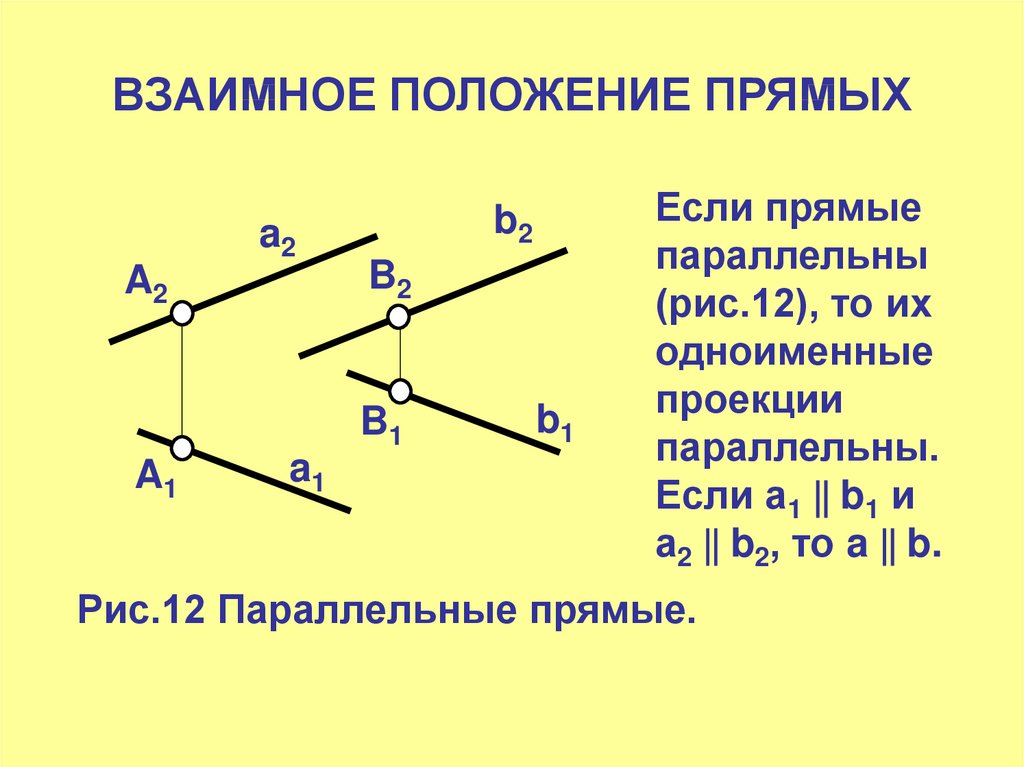
15. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

a2
A2
b2
B2
B1
A1
a1
b1
Если прямые
параллельны
(рис.12), то их
одноименные
проекции
параллельны.
Если а1 b1 и
а2 b2, то a b.
Рис.12 Параллельные прямые.

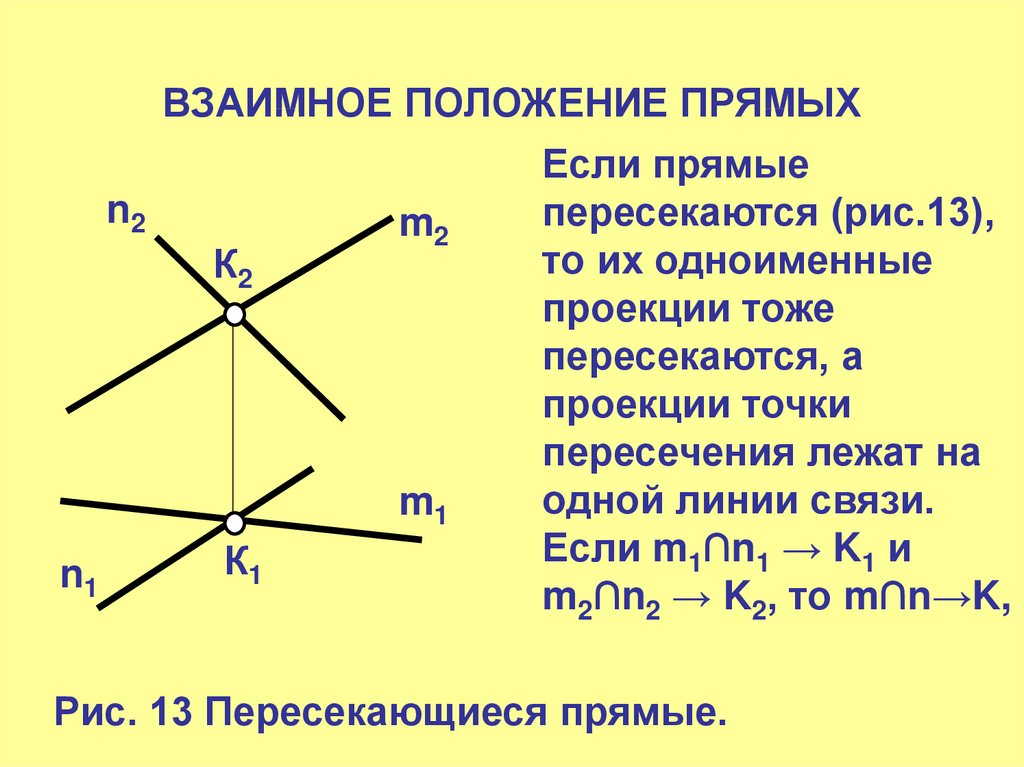
16. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

n2
К2
m2
m1
n1
К1
Если прямые
пересекаются (рис.13),
то их одноименные
проекции тоже
пересекаются, а
проекции точки
пересечения лежат на
одной линии связи.
Если m1∩n1 → K1 и
m2∩n2 → K2, то m∩n→K,
Рис. 13 Пересекающиеся прямые.

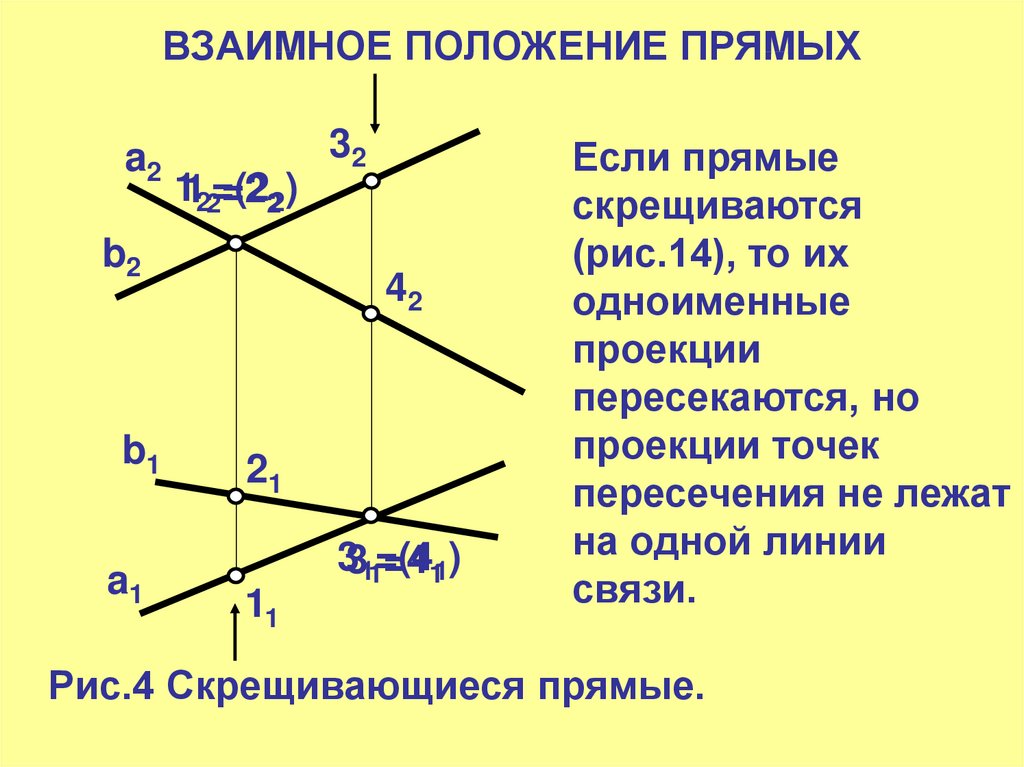
17. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

a2
32
1122=(2
=222)
b2
b1
a1
42
21
11
3311=(4
=411)
Если прямые
скрещиваются
(рис.14), то их
одноименные
проекции
пересекаются, но
проекции точек
пересечения не лежат
на одной линии
связи.
Рис.4 Скрещивающиеся прямые.