Проецирование прямой линии

1. Проецирование прямой линии

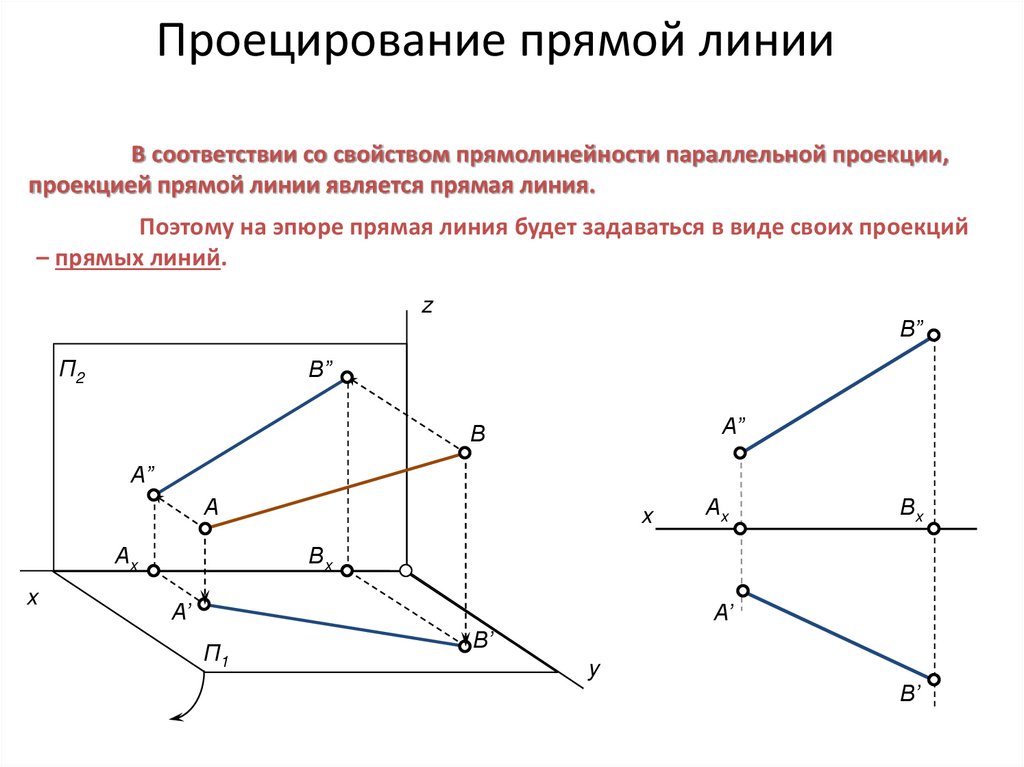
В соответствии со свойством прямолинейности параллельной проекции,
проекцией прямой линии является прямая линия.
Поэтому на эпюре прямая линия будет задаваться в виде своих проекций
– прямых линий.
z
П2
B”
B”
A”
В
A”
А
Аx
x
x
Аx
Вx
Вx
A’
A’
П1
B’
y
B’

2.

Проецирование прямой линии
Прямые частного положения
Прямой общего положения называется прямая не параллельная и не
перпендикулярная ни к одной из плоскостей проекций.
Прямые перпендикулярные или параллельные плоскостям проекций
называются прямыми частного положения.
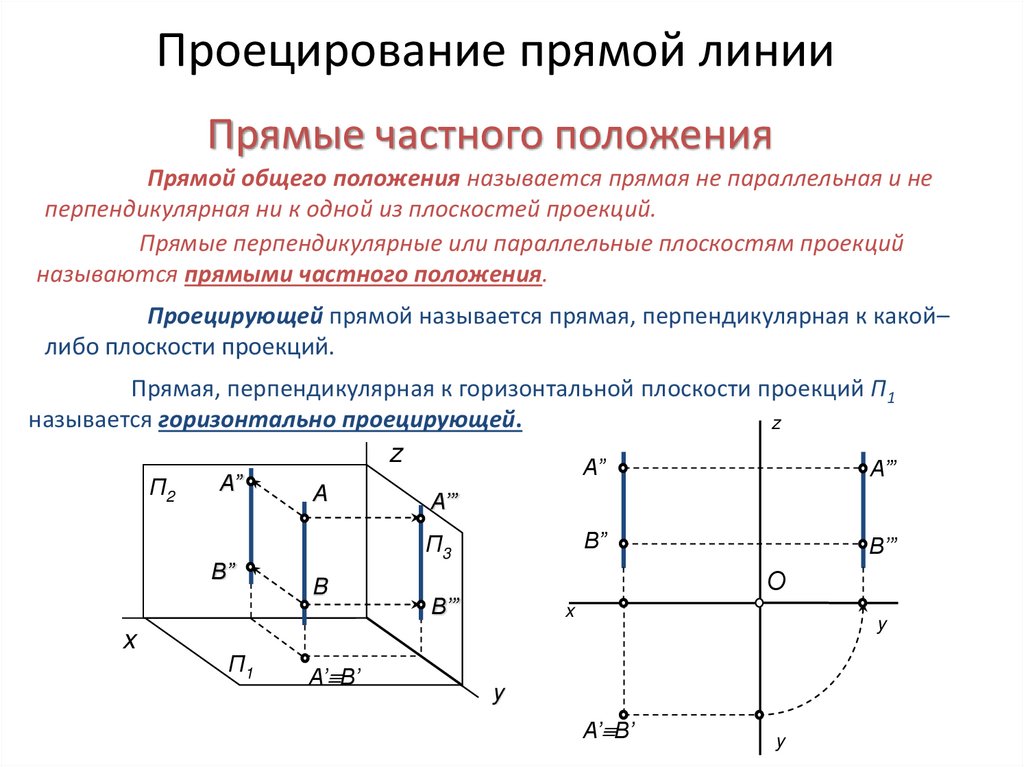
Проецирующей прямой называется прямая, перпендикулярная к какой–
либо плоскости проекций.
Прямая, перпендикулярная к горизонтальной плоскости проекций П1
называется горизонтально проецирующей.
z
z
П2
A”
B”
x
П1
A
A’ B’
A’”
B”
B’”
A’”
П3
B
A”
О
B’”
x
y
y
A’ B’
y

3.

Проецирование прямой линии
Прямые частного положения
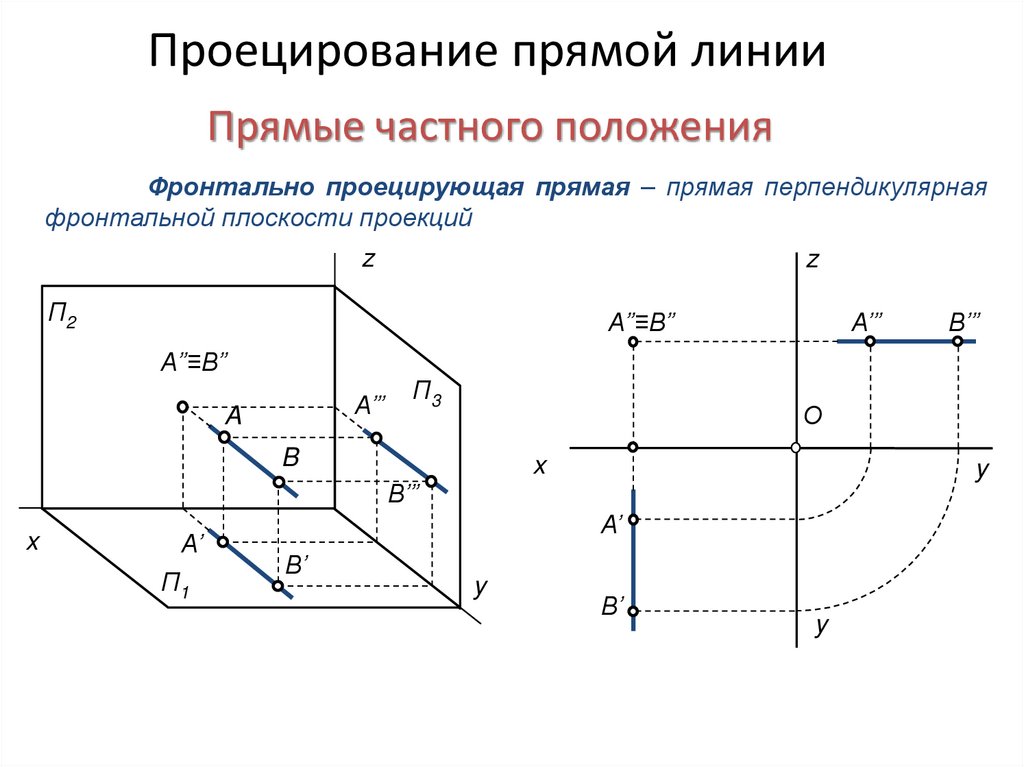
Фронтально проецирующая прямая – прямая перпендикулярная
фронтальной плоскости проекций
z
z
П2
A”≡B”
A”≡B”
A’” П33
A
A’”
О
B
x
y
B’”
x
A’
П1
A’
B’
B’”
y
B’
y

4.

Проецирование прямой линии
Прямые частного положения
Профильно проецирующая прямая – прямая перпендикулярная
профильной плоскости проекций
z
z
П2
B”
A”
B
B”
П3
A”
A’”≡B’”
П3
A A’”≡B’”
x
y
x
П1
B’
A’
y
B’
A’
y

5.

Проецирование прямой линии
Прямые частного положения
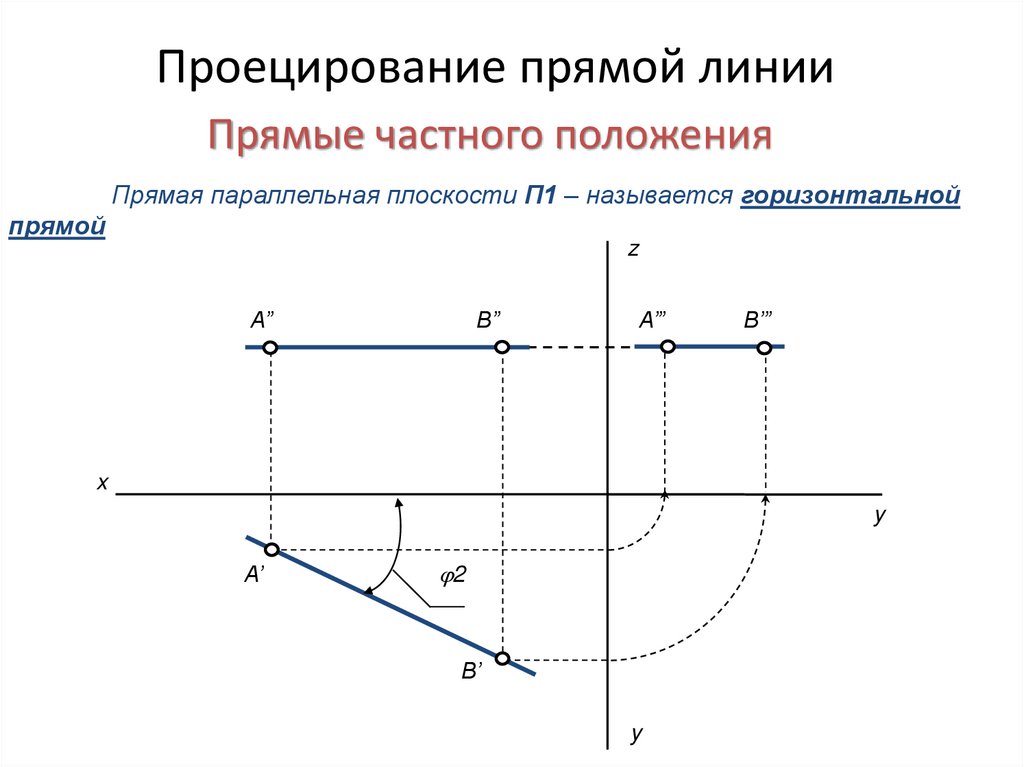
Прямая параллельная плоскости П1 – называется горизонтальной
прямой
z
A”
B”
A’”
B’”
x
y
A’
2
B’
y

6.

Проецирование прямой линии
Прямые частного положения
Прямая параллельная плоскости П2 – называется фронтальной
прямой
z
B”
B’”
A”
A’”
1
y
x
A’
B’
y

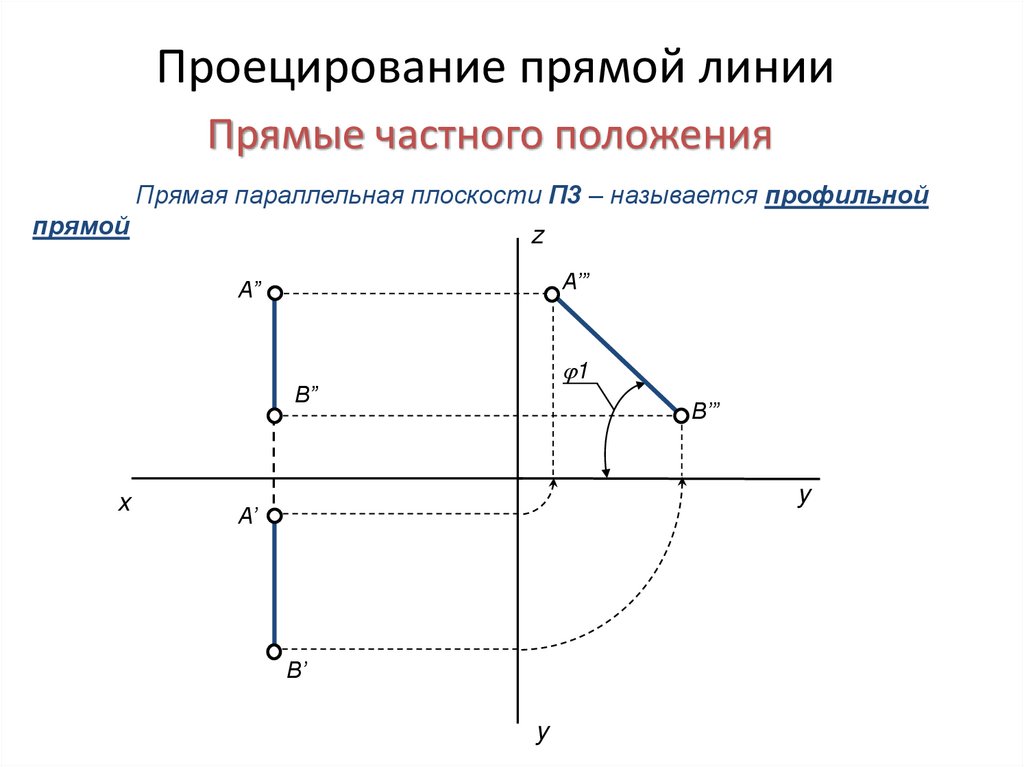
7.

Проецирование прямой линии
Прямые частного положения
Прямая параллельная плоскости П3 – называется профильной
прямой
z
A’”
A”
1
B”
x
B’”
y
A’
B’
y

8.

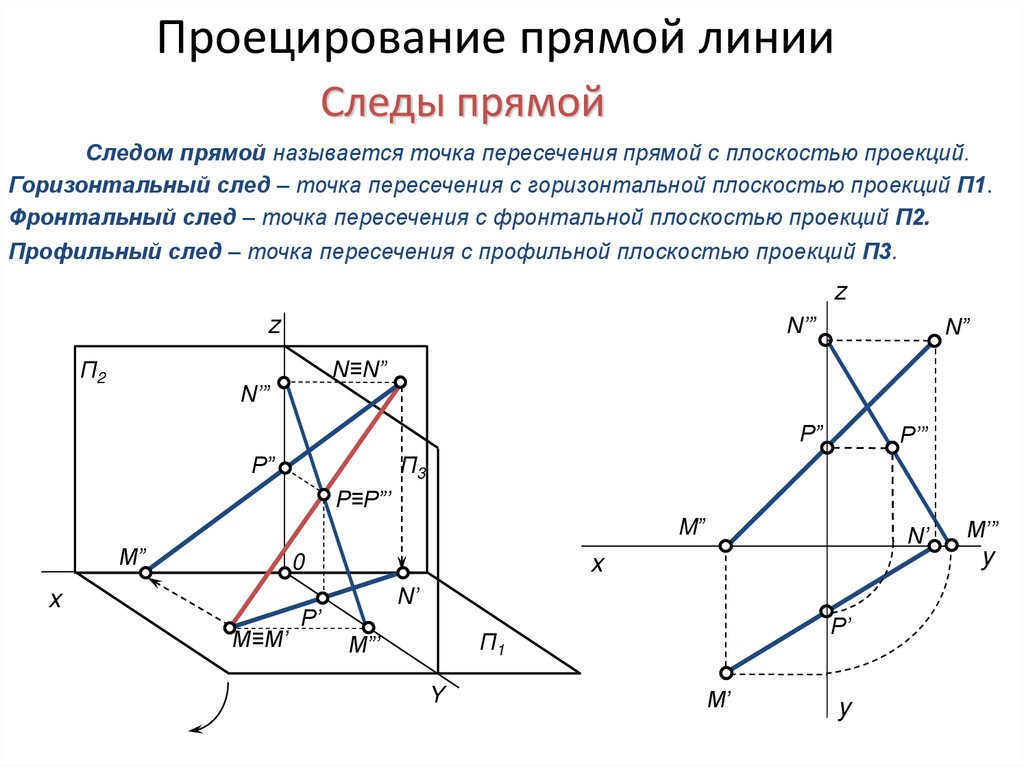
Проецирование прямой линии
Следы прямой
Следом прямой называется точка пересечения прямой с плоскостью проекций.
Горизонтальный след – точка пересечения с горизонтальной плоскостью проекций П1.
Фронтальный след – точка пересечения с фронтальной плоскостью проекций П2.
Профильный след – точка пересечения с профильной плоскостью проекций П3.
z
N’”
z
П2
N”
N≡N”
N’”
P”
P”
P’”
П3
P≡P”’
M”
M”
0
x
M≡M’
N’
x
N’
P’
P’
П1
M”’
Y
M’
y
M’”
y

9.

Проецирование прямой линии
Взаимное положение точки и прямой
проекцией точки, лежащей на некоторой прямой, является
точка, лежащая на проекции этой прямой
D”
B”
E’
m”
C”
A”
x
C’
E”
A’
B’
D’
m’

10.

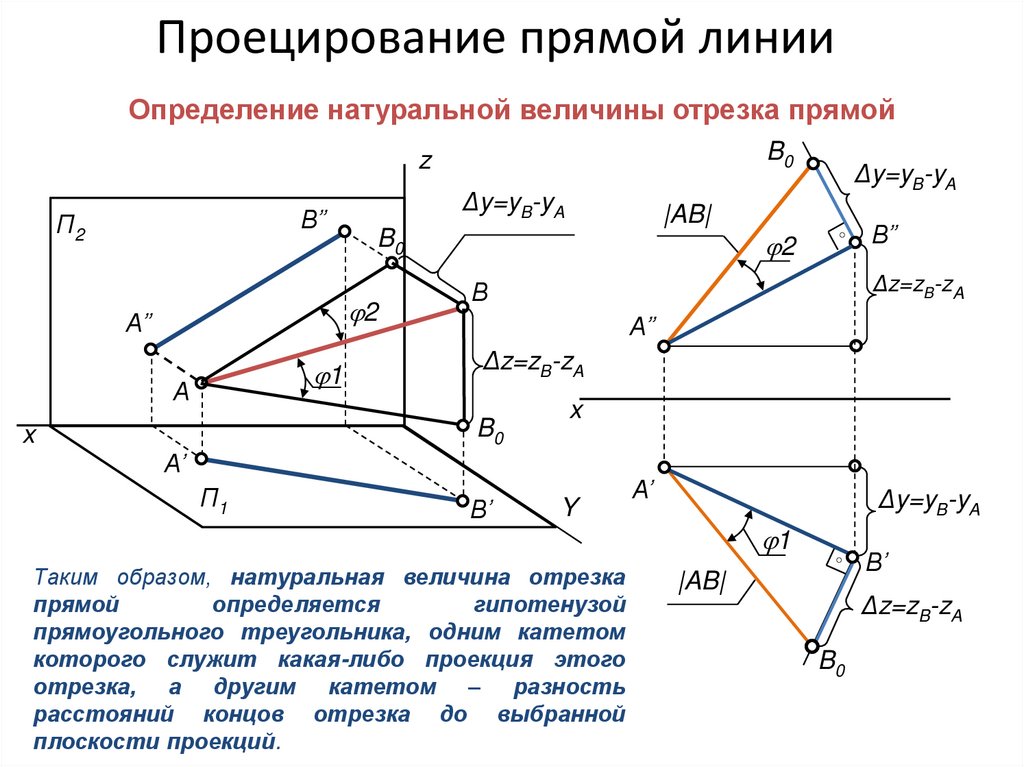
Проецирование прямой линии
Определение натуральной величины отрезка прямой
B0
z
B”
П2
Δy=yB-yA
B0
2
A”
1
А
Δz=zB-zA
A”
Δz=zB-zA
x
A’
П1
B”
2
В
B0
x
|AB|
Δy=yB-yA
B’
Y
Таким образом, натуральная величина отрезка
прямой
определяется
гипотенузой
прямоугольного треугольника, одним катетом
которого служит какая-либо проекция этого
отрезка, а другим катетом – разность
расстояний концов отрезка до выбранной
плоскости проекций.
A’
Δy=yB-yA
1
B’
|AB|
Δz=zB-zA
B0

11.

Проецирование прямой линии
Взаимное положение прямых
Две
могут:
прямые
в
пространстве
• пересекаться;
• скрещиваться;
Одноимённые проекции пересекающихся • быть параллельными.
прямых пересекаются между собой. Причем
Одноимённые проекции скрещивающихся прямых
точки
пересечения
проекций,
в могут пересекаться или не пересекаться. Если же они
соответствии
со
свойством пересекаются, то точки пересечения лежат на разных
принадлежности параллельной проекции, линиях связи.
должны лежать на одной линии связи .
m”
1”
1”
3” 4”
n”
s”
2”
t”
x
x
n’
t’
4’
m’
1’
1’ 2’
s’
3’

12.

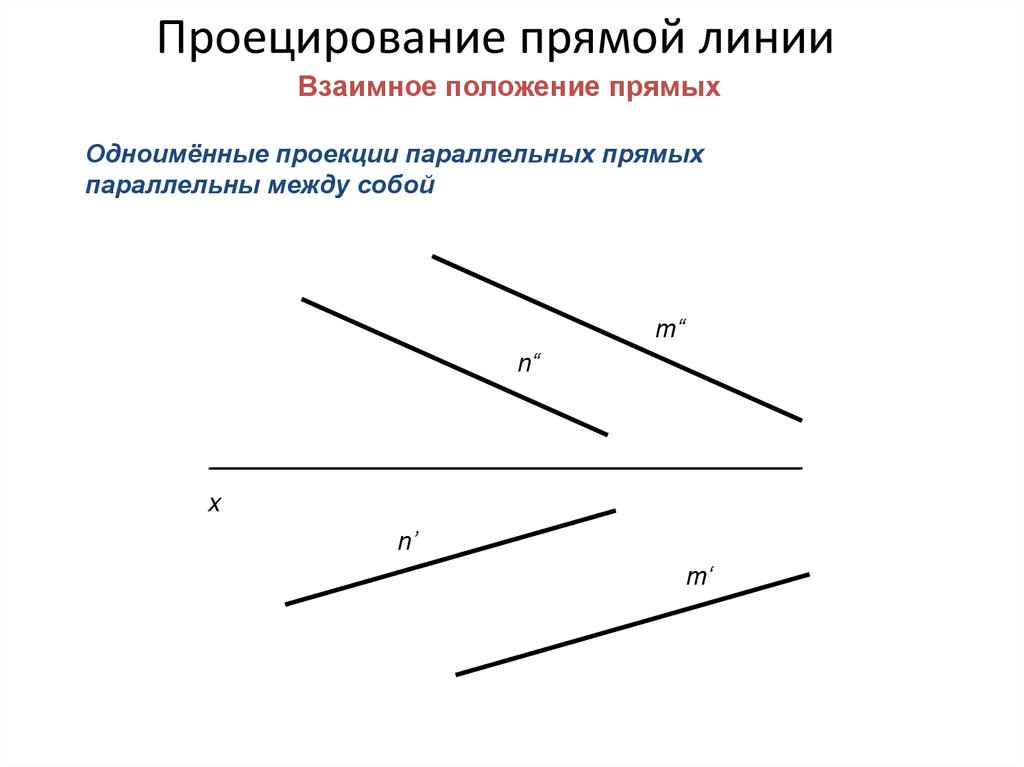
Проецирование прямой линии
Взаимное положение прямых
Одноимённые проекции параллельных прямых
параллельны между собой
m“
n“
x
n’
m‘

13.

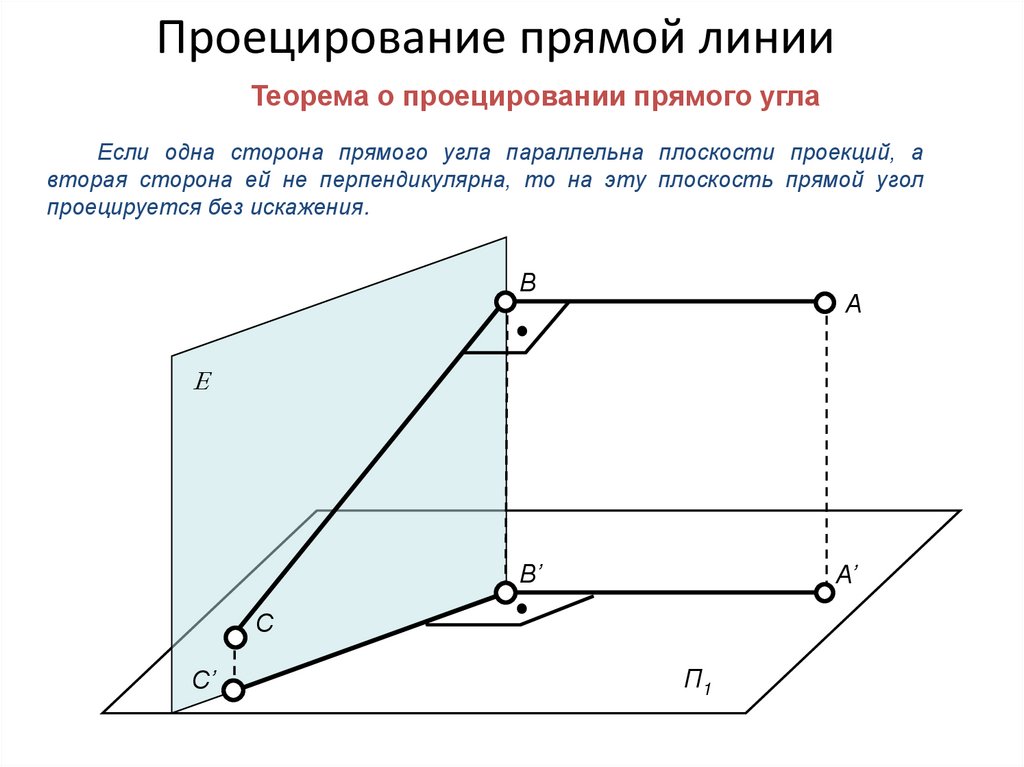
Проецирование прямой линии
Теорема о проецировании прямого угла
Если одна сторона прямого угла параллельна плоскости проекций, а
вторая сторона ей не перпендикулярна, то на эту плоскость прямой угол
проецируется без искажения.
В
А
B’
A’
С
C’
П1