Похожие презентации:
Прямая. Ортогональные проекции прямой линии
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Лекция 2. Прямая
Пьянкова Жанна Анатольевна,доцент каф. «ПиЭА», канд. пед. наук
1
2. Лекция 2. Ортогональные проекции прямой линии
Лекция 2.Ортогональные проекции
прямой линии
Способы задания прямой линии
Прямые общего положения
Прямые частного положения
Метод прямоугольного треугольника
Взаимное положение двух прямых
Свойство проекций прямого плоского
угла
2
3. Прямая линия – кратчайшее расстояние между двумя точками
Задание прямой линии:1. Аналитическим способом
2. Графическими способами
3
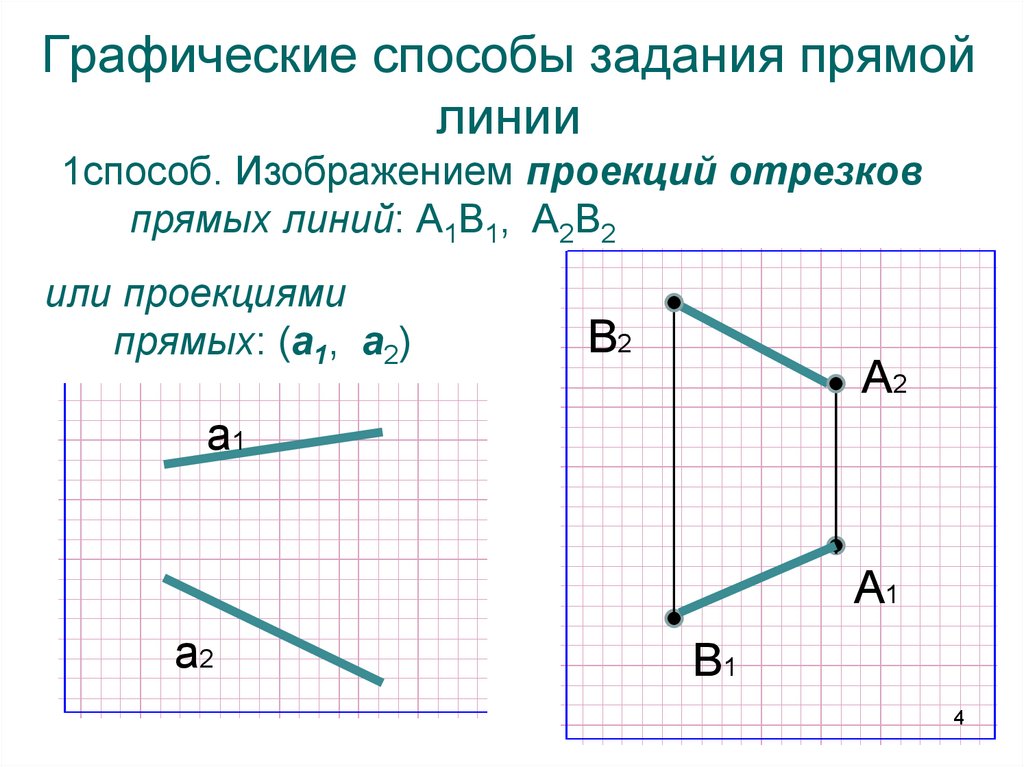
4. Графические способы задания прямой линии
1способ. Изображением проекций отрезковпрямых линий: A1B1, A2B2
или проекциями
прямых: (а1, а2)
B2
А2
а1
А1
а2
B1
4
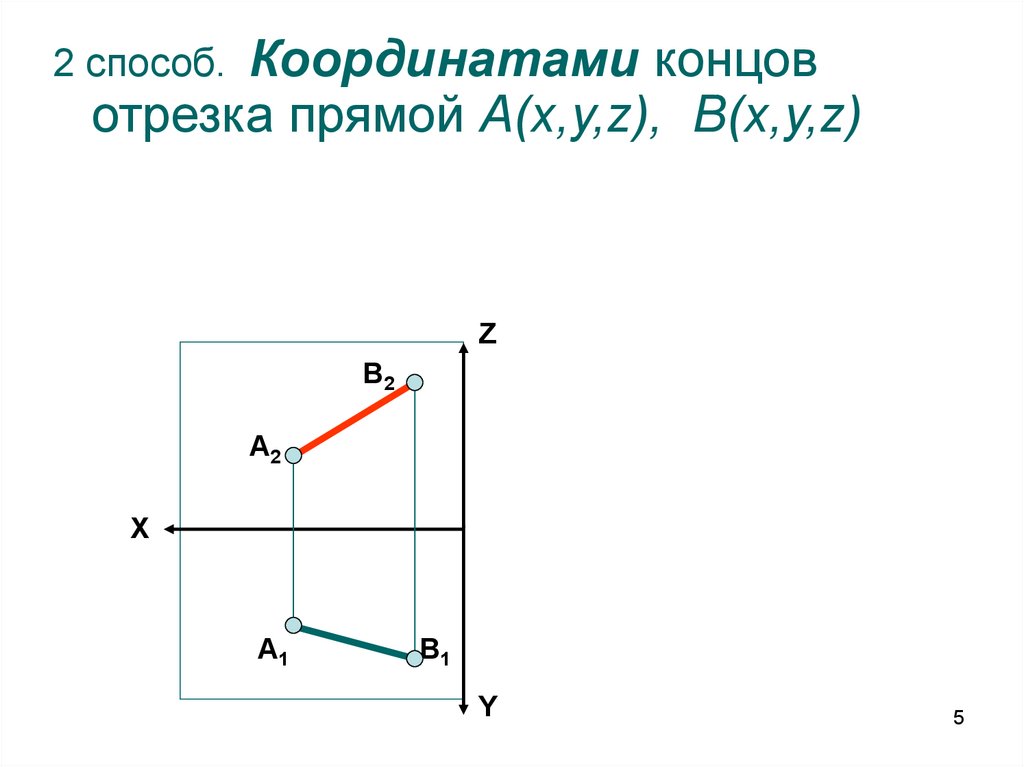
5.
Координатами концовотрезка прямой А(x,y,z), В(x,y,z)
2 способ.
Z
В2
А2
X
А1
В1
Y
5
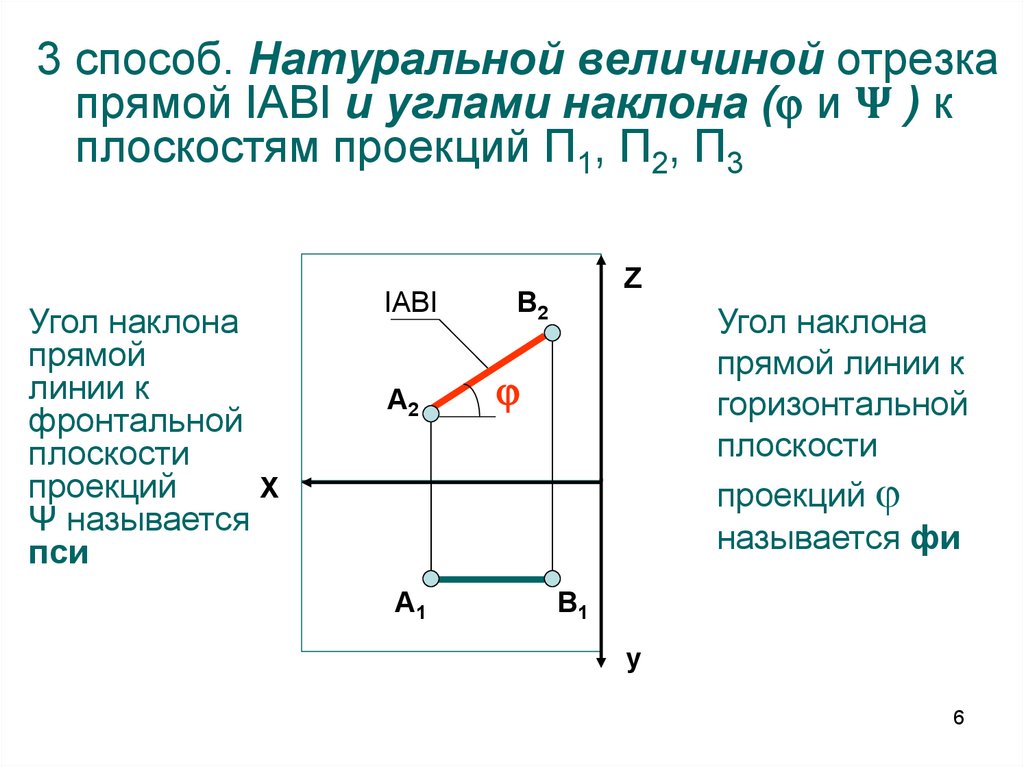
6.
3 способ. Натуральной величиной отрезкапрямой IABI и углами наклона ( и Ψ ) к
плоскостям проекций П1, П2, П3
Угол наклона
прямой
линии к
фронтальной
плоскости
проекций
X
Ψ называется
пси
IАВI
А2
А1
Z
В2
Угол наклона
прямой линии к
горизонтальной
плоскости
проекций
называется фи
В1
y
6
7. 4 способ. Задание прямой ее следами
• Следом прямой линииназывается точка пересечения
прямой с плоскостью проекций
У прямой линии может быть три следа,
которые образуются при пересечении с
горизонтальной, фронтальной и
профильной плоскостями
7
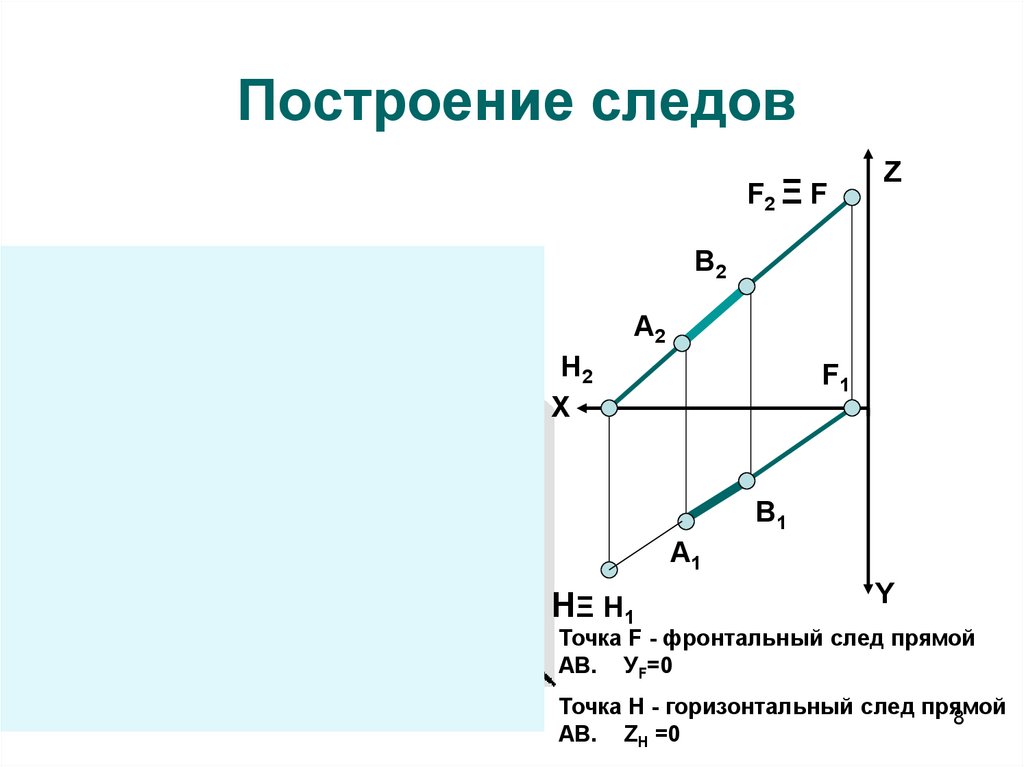
8. Построение следов
F2 Ξ FВ2
Z
П2
Z
А2
В2
А2
H2
H2
X
F2ΞF
B
А
П3
X
В1
F1
H1ΞH
F1
А1
П1
А1
В1
HΞ H1
Y
Y
Точка F - фронтальный след прямой
АВ. УF=0
Точка H - горизонтальный след прямой
8
АВ. ZН =0
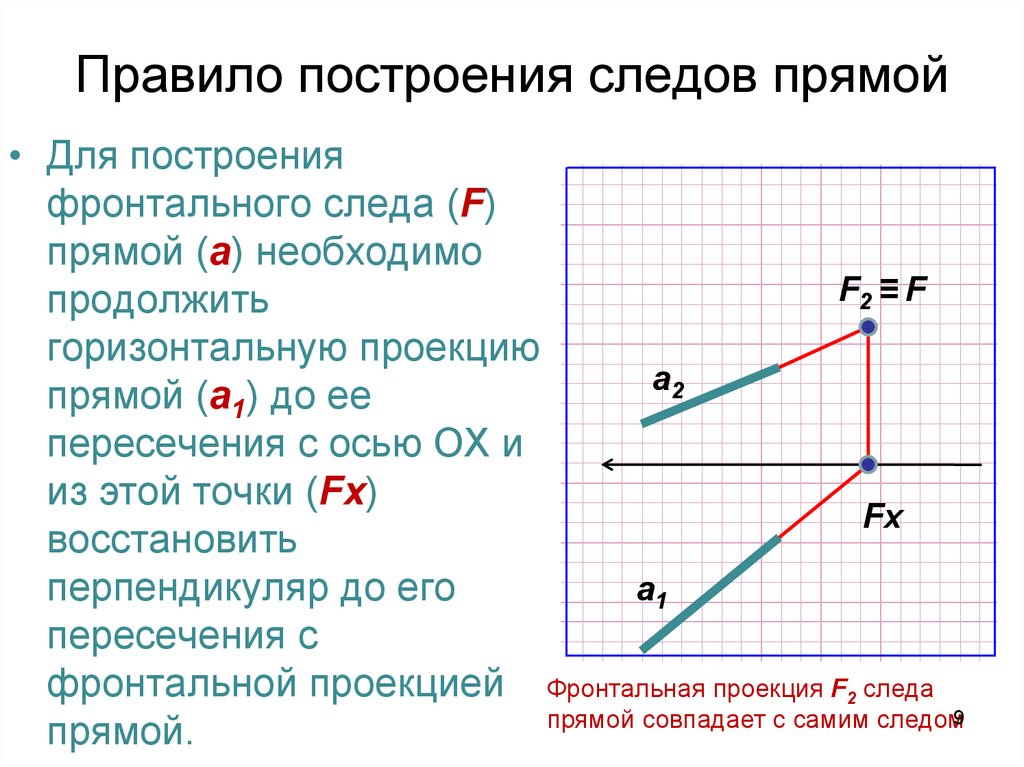
9. Правило построения следов прямой
• Для построенияфронтального следа (F)
прямой (а) необходимо
F2 ≡ F
продолжить
горизонтальную проекцию
а2
прямой (а1) до ее
пересечения с осью ОХ и
из этой точки (Fх)
Fх
восстановить
а1
перпендикуляр до его
пересечения с
фронтальной проекцией Фронтальная проекция F2 следа
прямой совпадает с самим следом9
прямой.
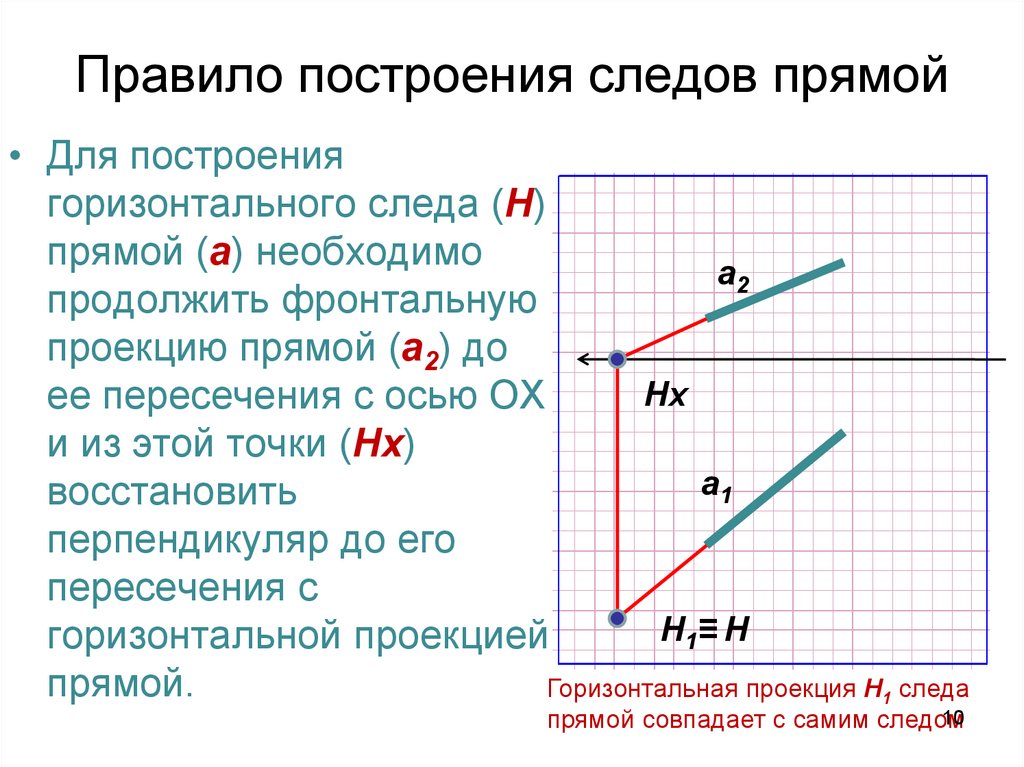
10. Правило построения следов прямой
• Для построениягоризонтального следа (H)
прямой (а) необходимо
а2
продолжить фронтальную
проекцию прямой (а2) до
Hх
ее пересечения с осью ОХ
и из этой точки (Hх)
а1
восстановить
перпендикуляр до его
пересечения с
H1≡ H
горизонтальной проекцией
прямой.
Горизонтальная проекция H1 следа
10
прямой совпадает с самим следом
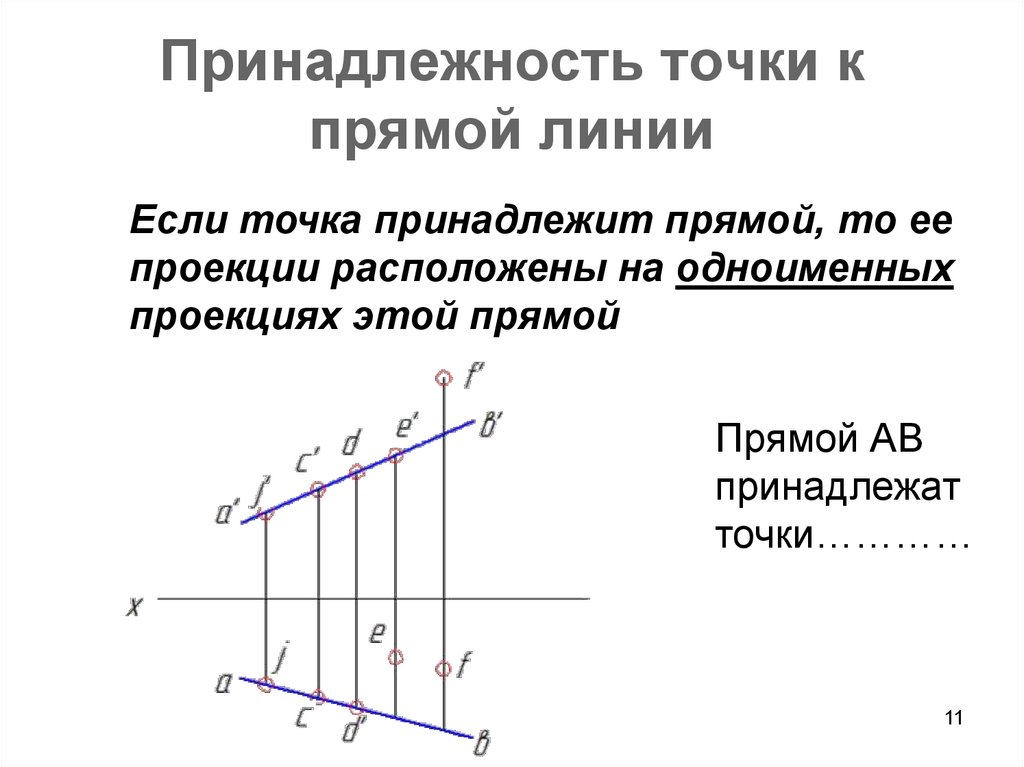
11. Принадлежность точки к прямой линии
Если точка принадлежит прямой, то еепроекции расположены на одноименных
проекциях этой прямой
Прямой АВ
принадлежат
точки…………
11
12. Положение прямой относительно плоскостей проекций:
1. Параллельно – прямые уровня(горизонталь, фронталь, профильная
прямая)
2. Перпендикулярно – проецирующие
прямые
3. Под углом, отличным от прямого –
прямые общего положения
12
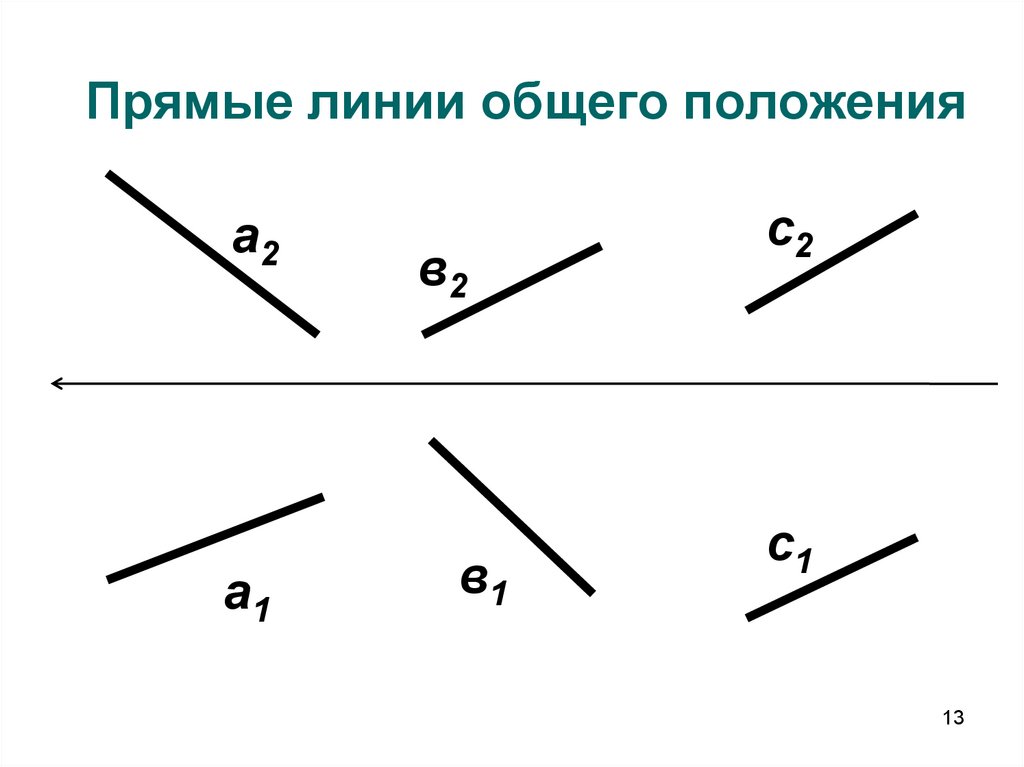
13. Прямые линии общего положения
а2а1
в2
в1
с2
с1
13
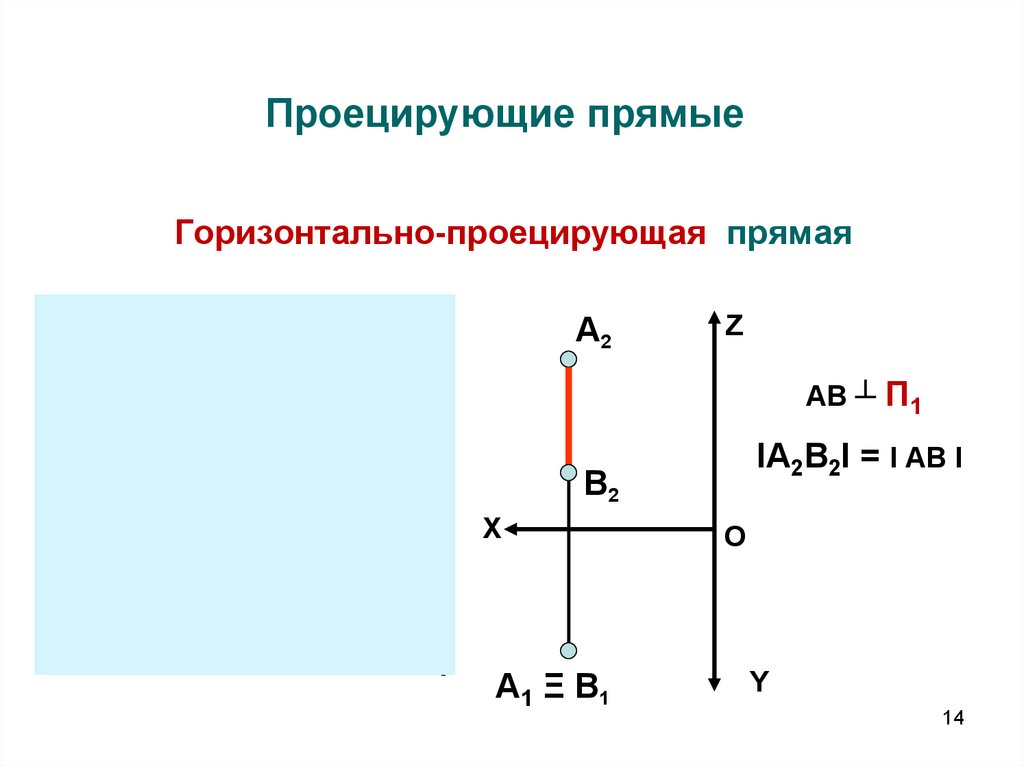
14. Проецирующие прямые
Горизонтально-проецирующая прямаяZ
А2
А2
Z
AB ┴ П1
А
B2
X
B
IА2В2I = I АВ I
B2
О
X
О
А1 Ξ B
1
Y
А1 Ξ B1
Y
14
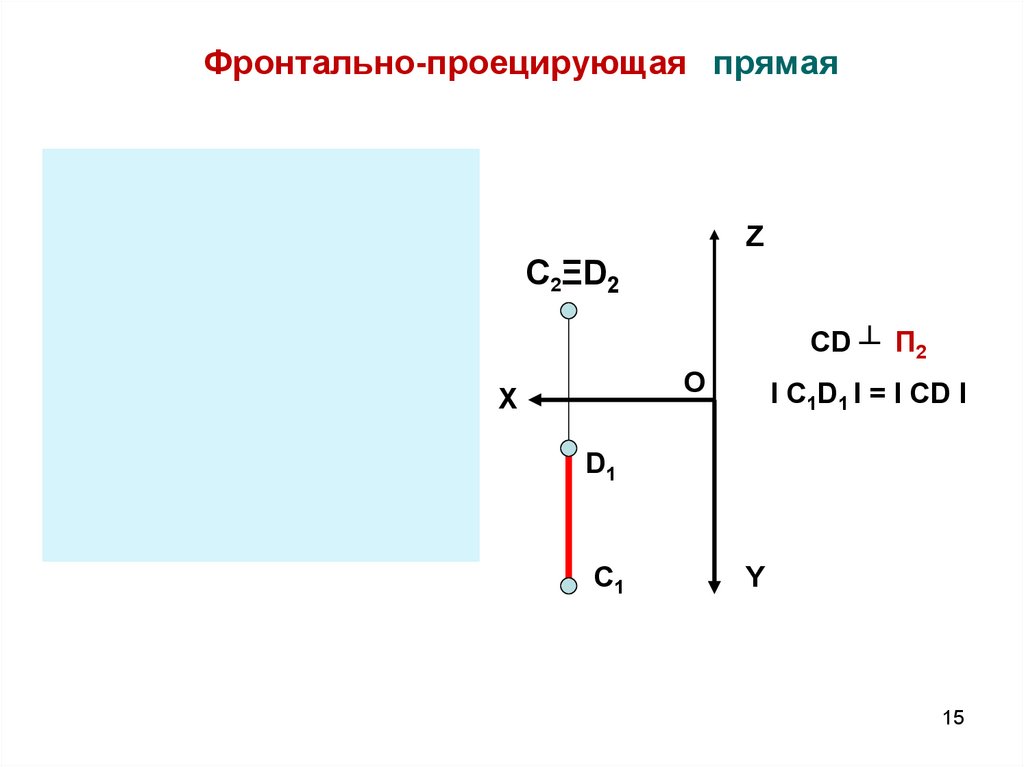
15.
Фронтально-проецирующая прямаяZ
Z
C2ΞD2
C2Ξ D2
D
CD ┴ П2
C
X
О
X
D1
I C1D1 I = I CD I
D1
C1
Y
C1
Y
15
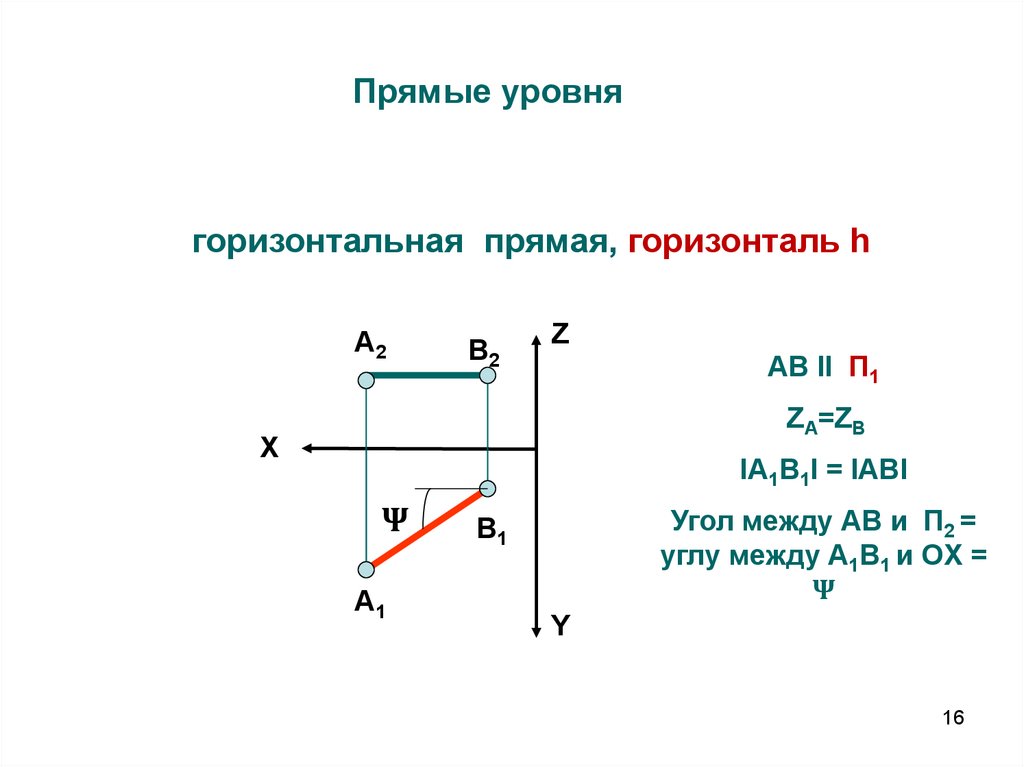
16. Прямые уровня
горизонтальная прямая, горизонталь hА2
В2
Z
AВ II П1
ZА=ZB
X
IА1В1I = IАВI
Ψ
А1
Угол между АВ и П2 =
углу между А1В1 и ОX =
Ψ
В1
Y
16
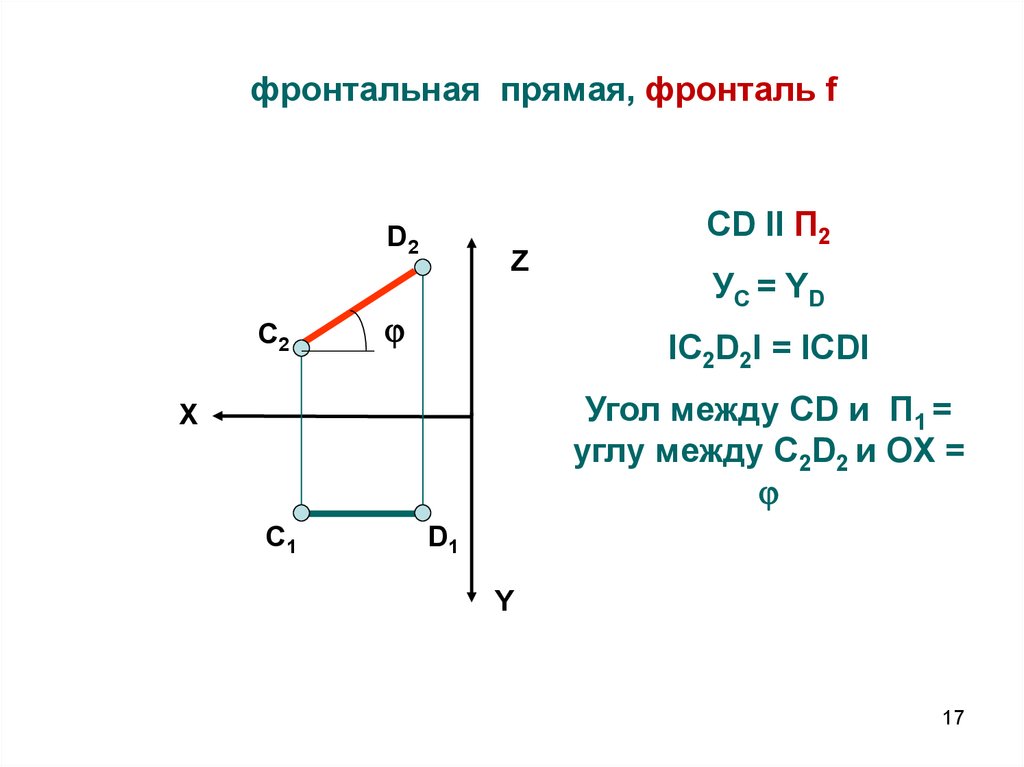
17.
фронтальная прямая, фронталь fCD II П2
D2
C2
Z
УС = YD
IС2D2I = ICDI
Угол между CD и П1 =
углу между С2D2 и ОX =
X
C1
D1
Y
17
18. Определение натуральной величины отрезка прямой общего положения МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
ДЛИНА ОТРЕЗКА РАВНАГИПОТЕНУЗЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА,
ОДИН КАТЕТ КОТОРОГО РАВЕН ПРОЕКЦИИ
ОТРЕЗКА, А ДРУГОЙ – РАЗНОСТИ КООРДИНАТ
КОНЦОВ ОТРЕЗКА ОТ ЭТОЙ ЖЕ ПЛОСКОСТИ
18
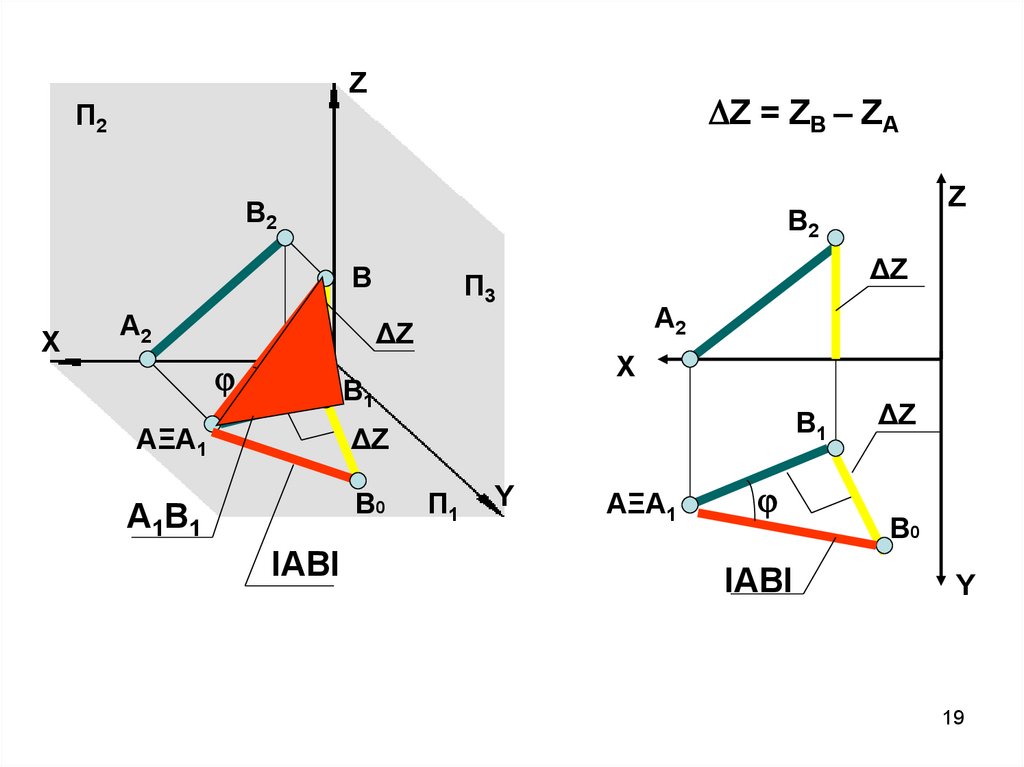
19.
ZZ = ZB – ZA
П2
В2
В2
В
X
А2
ΔZ
П3
А2
ΔZ
X
В1
АΞА1
ΔZ
А1В1
В0
IABI
Z
В1
П1
Y
АΞА1
IABI
ΔZ
В0
Y
19
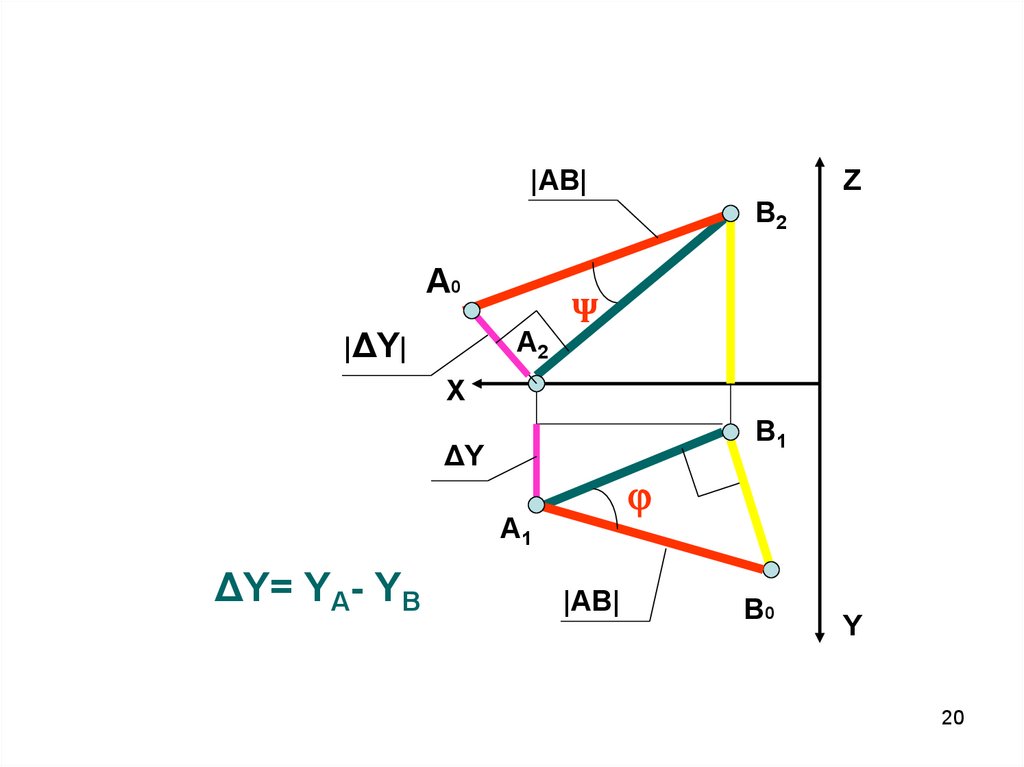
20.
|АВ|Z
В2
А0
А2
|ΔY|
Ψ
X
В1
ΔY
А1
ΔY= YA- YB
|АВ|
В0
Y
20
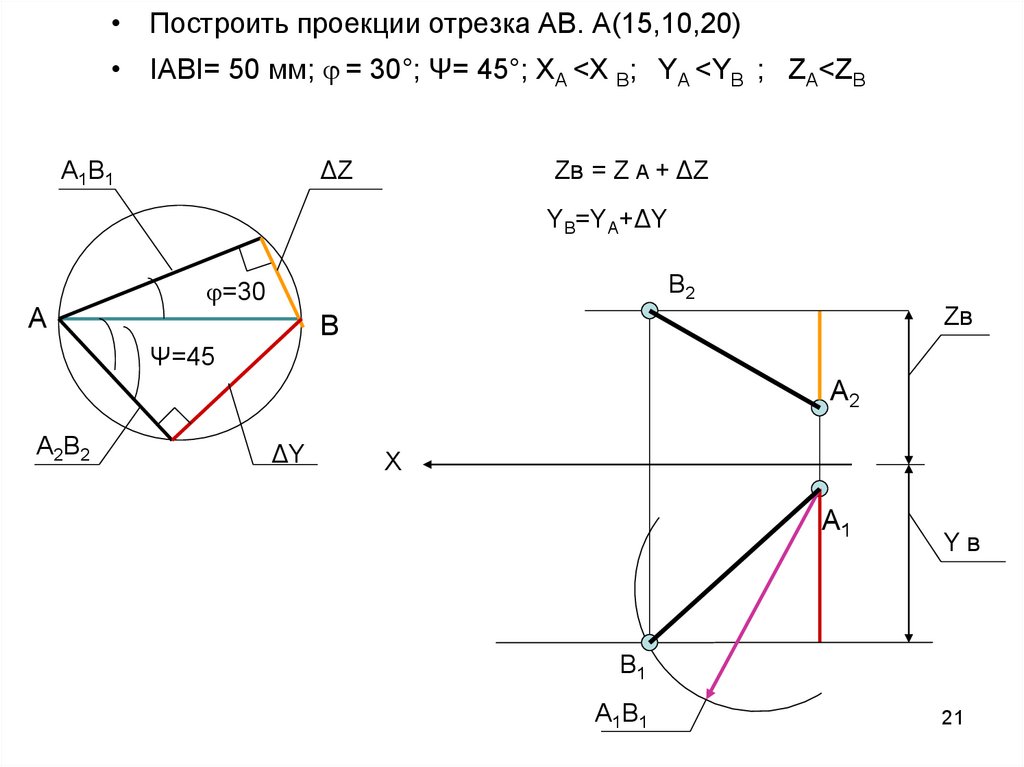
21.
• Построить проекции отрезка АВ. А(15,10,20)• IАВI= 50 мм; = 30°; Ψ= 45°; XА <X В; YA <YВ ; ZA<ZВ
А1В1
ΔZ
Zв = Z А + ΔZ
YВ=YА+ΔY
А
В2
=30
Zв
В
Ψ=45
A2
А2В2
ΔY
X
А1
Yв
В1
А1В1
21
22. Относительное положение прямых
Прямые в пространстве могут быть расположены:1. Параллельно
2. Перпендикулярно
3. Пересекаться
4. Скрещиваться
22
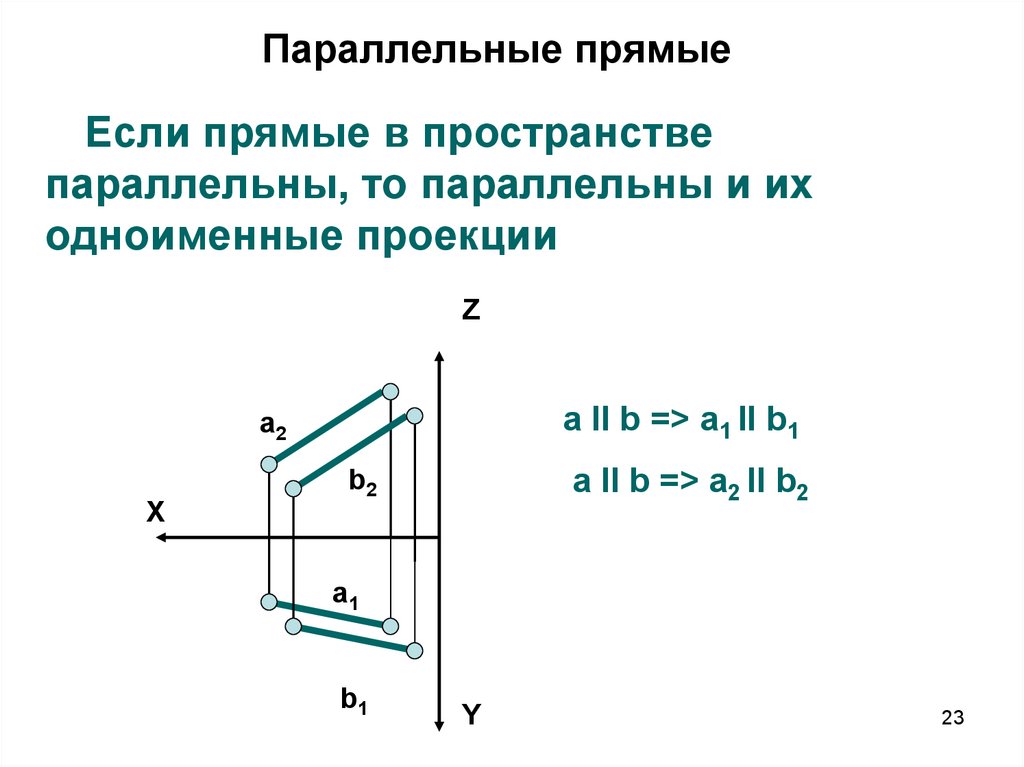
23. Параллельные прямые
Если прямые в пространствепараллельны, то параллельны и их
одноименные проекции
Z
a II b => a1 II b1
а2
a II b => a2 II b2
b2
X
a1
b1
Y
23
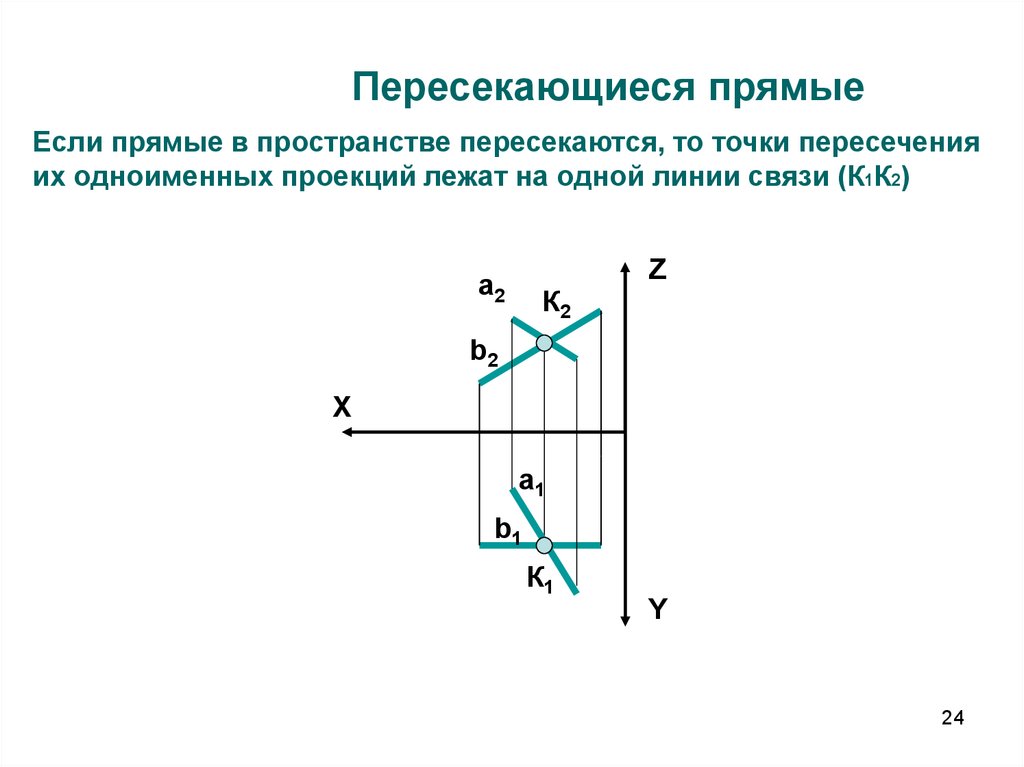
24. Пересекающиеся прямые
Если прямые в пространстве пересекаются, то точки пересеченияих одноименных проекций лежат на одной линии связи (К1К2)
Z
a2
К2
b2
X
a1
b1
К1
Y
24
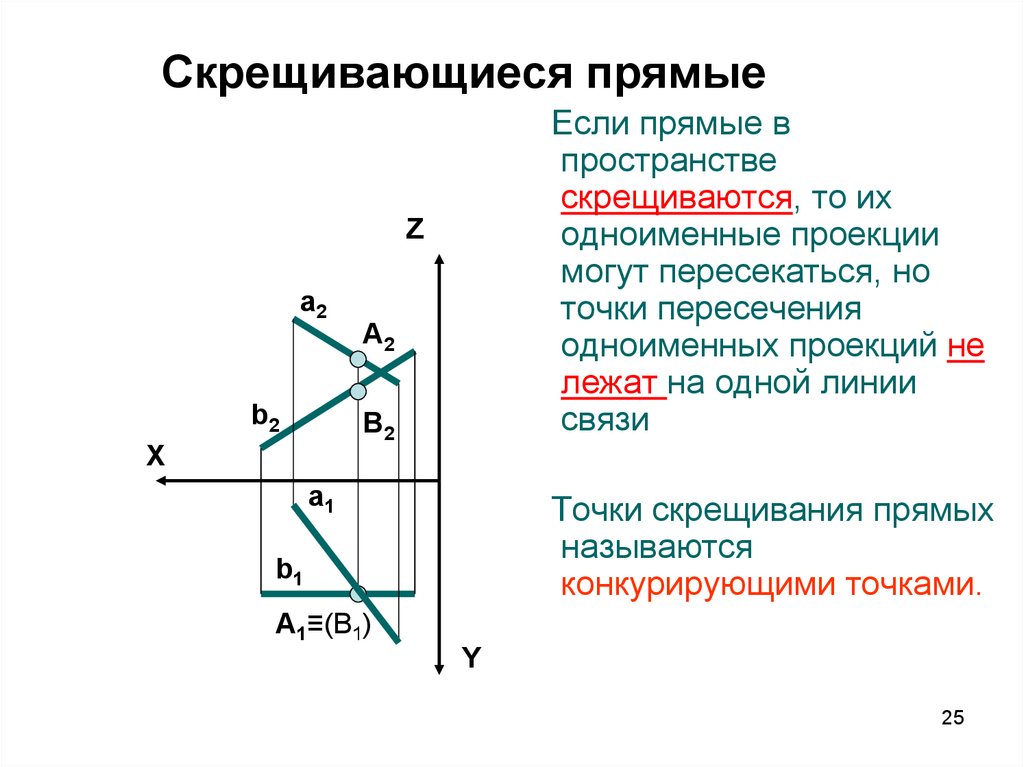
25. Скрещивающиеся прямые
Если прямые впространстве
cкрещиваются, то их
одноименные проекции
могут пересекаться, но
точки пересечения
одноименных проекций не
лежат на одной линии
связи
Z
a2
b2
А2
В2
X
a1
Точки скрещивания прямых
называются
конкурирующими точками.
b1
А1≡(В1)
Y
25
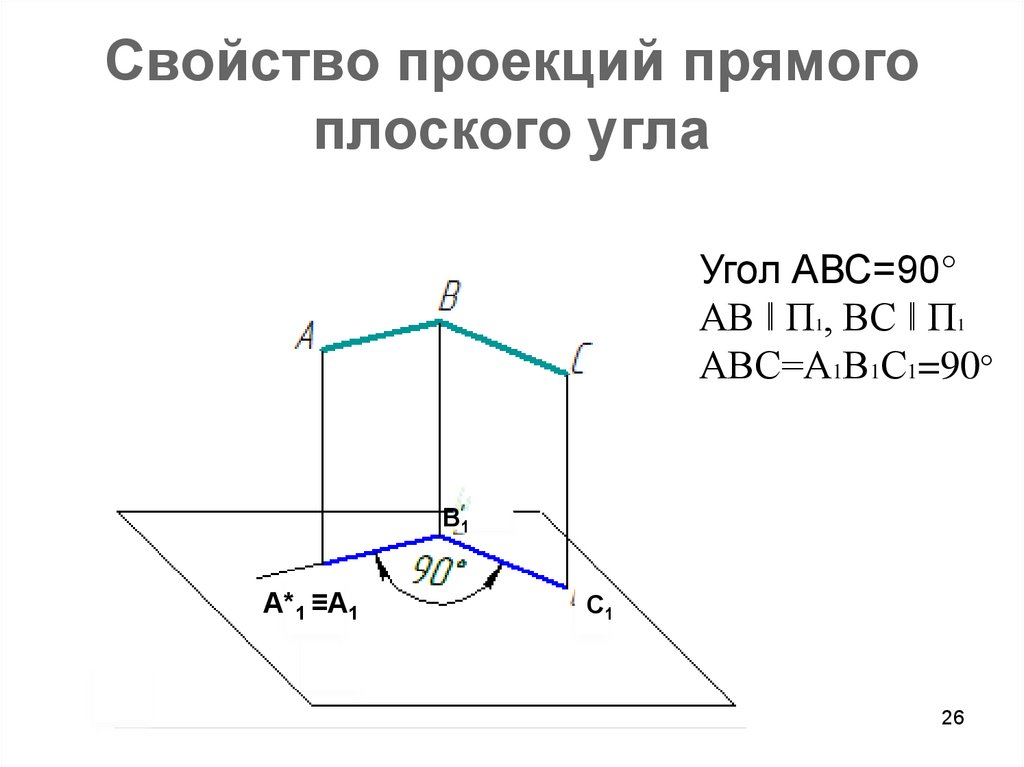
26. Свойство проекций прямого плоского угла
Угол АВС=90°АВ ǁ П1, ВС ǁ П1
АВС=А1В1С1=90°
В1
А*1 ≡А1
С1
26
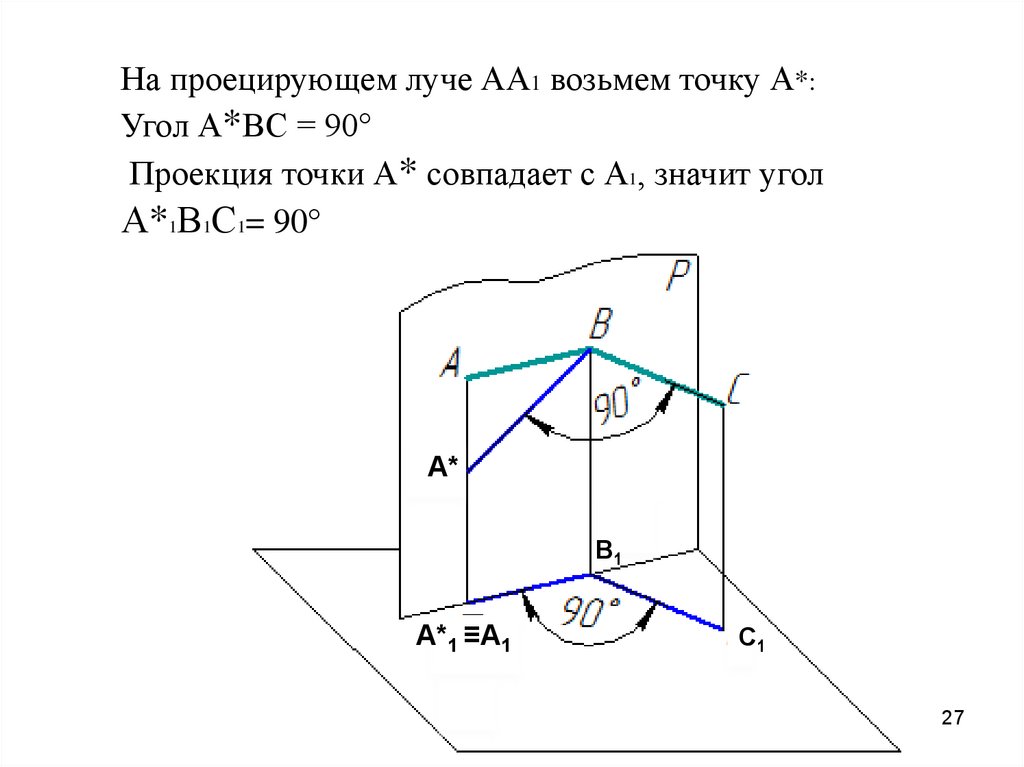
27.
На проецирующем луче АА1 возьмем точку А*:Угол А*ВС = 90°
Проекция точки А* совпадает с А1, значит угол
А*1В1С1= 90°
А*
В1
А*1 ≡А1
С1
27
28. Свойство проекций прямого плоского угла
Если одна сторона прямого плоскогоугла параллельна плоскости
проекций, то прямой угол на эту
плоскость проецируется в
натуральную величину
28









 Математика
Математика Инженерная графика
Инженерная графика








