Проводники с током в магнитном поле. Теорема Гаусса для магнитного поля

1. Лекция № 7

ПРОВОДНИКИ С ТОКОМ В
МАГНИТНОМ ПОЛЕ.
ТЕОРЕМА ГАУССА ДЛЯ
МАГНИТНОГО ПОЛЯ

2. Закон Ампера

Закон Ампера определяет силу, с
которой внешнее магнитное поле
индукции
B
действует на элемент тока I d l
d F I dl B I dl , B
(7.1)
Сила
Ампера,
действующая
на
проводник с током в магнитном поле с
магнитной индукцией B
F I dl , B
l
(7.2)

3.

B const
Для однородного поля
и прямого отрезка проводника
F F I l B sin
(7.3)
Взаимодействие
двух
длинных
параллельных проводников с током
I1
B2
1
F21 F12
b
I2
B1
Сила
(7.3)
действия
поля,
l создаваемого током
I1, на ток I2.
F12 I 2 l B1

4.

B1 – магнитная индукция, создаваемая
током I1 в месте нахождения тока I2
0 I1
B1 0 H1
2 b
Величина силы притяжения
сонаправленных токов
0 I1 I 2 l
F12
2 b
Аналогично:
0 I1I 2l
F21
2 b
двух

5.

Параллельные
• сонаправленные токи притягиваются,
I1 I 2
I1
F21
1
B2
I2
b
• противоположно
направленные
B1
F12
l
I1 I 2
отталкиваются.

6.

pm
S
n
S
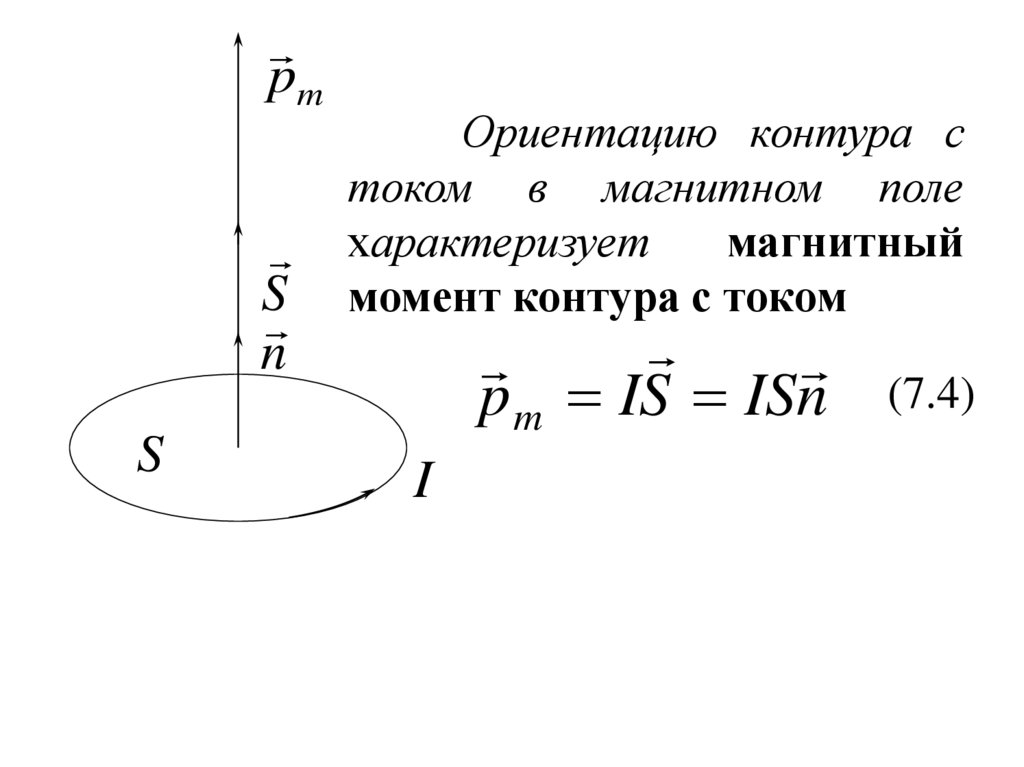
Ориентацию контура с
током в магнитном поле
характеризует
магнитный
момент контура с током
p m IS ISn
I
(7.4)

7.

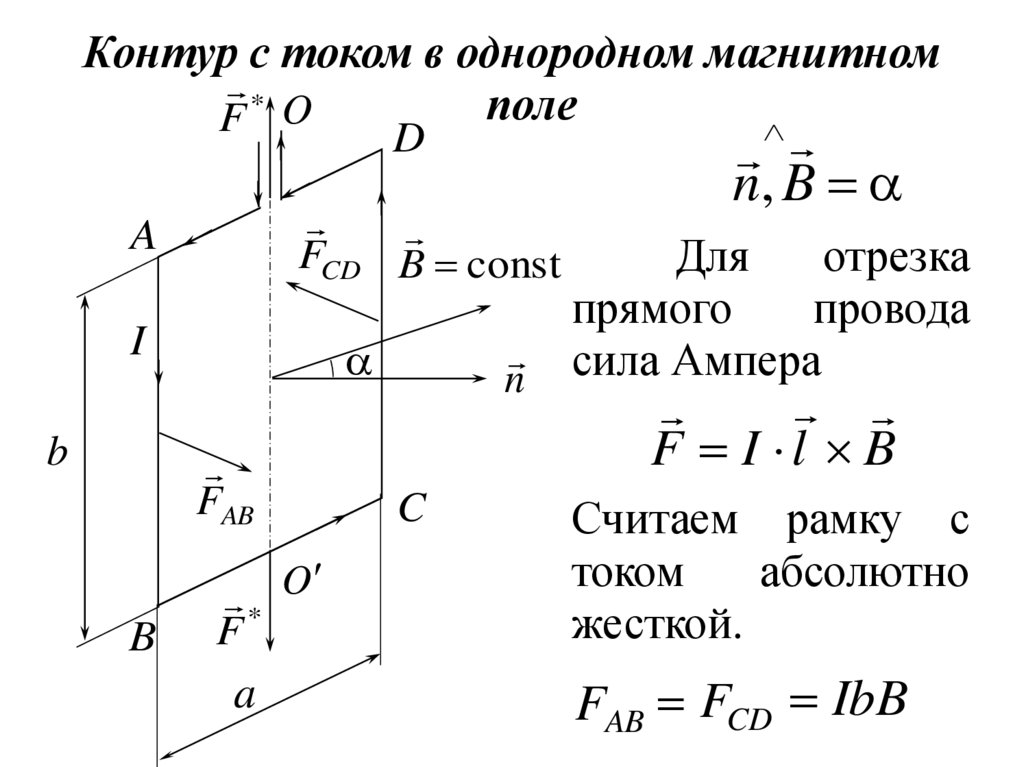
Контур с током в однородном магнитном
*
поле
F O
D
FCD B const
A
I
b
FAB
B
O
*
F
a
n
C
n, B
Для
отрезка
прямого
провода
сила Ампера
F I l B
Считаем рамку с
током
абсолютно
жесткой.
FAB FCD IbB

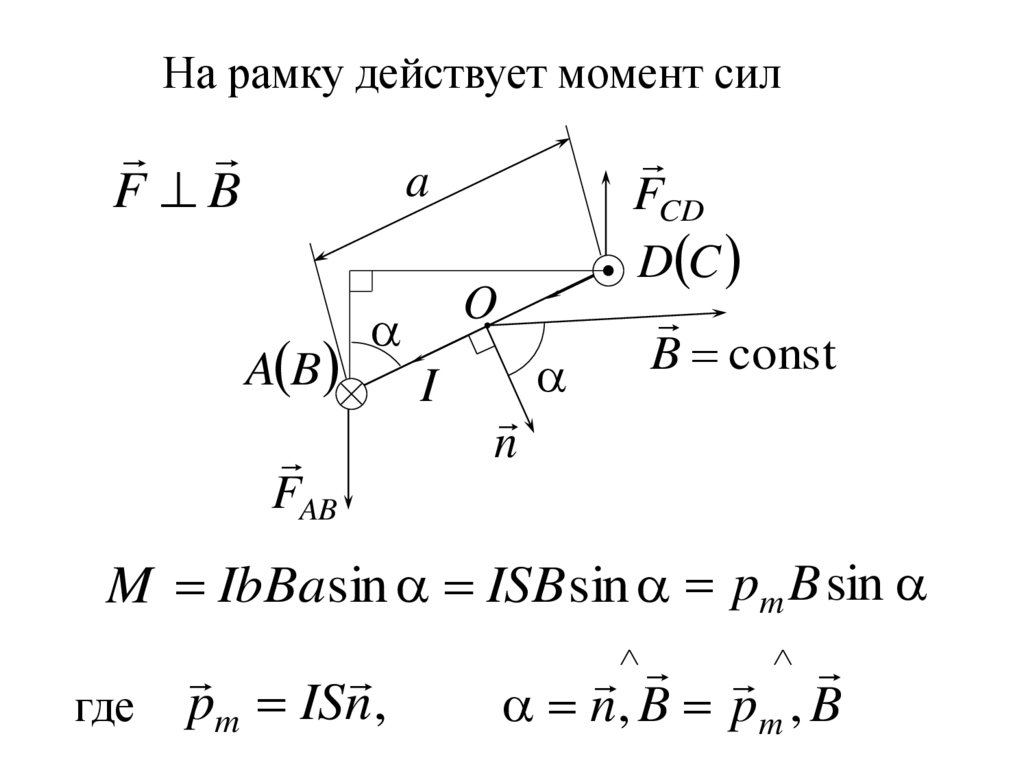
8. На рамку действует момент сил

F B
a
A B
FAB
O
I
n
FCD
D C
B const
M IbBasin ISB sin pm B sin
где pm ISn ,
n, B pm , B

9.

Момент пары сил, действующий на
контур с током в однородном магнитном поле
M pm B pm , B
(7.5)
Положение контура будет
• устойчивым при
pm B 0 M 0
• неустойчивым при
pm B M 0

10.

Во внешнем однородном магнитном поле на
контур с током действует вращающий
момент M , стремящийся
повернуть
контур так,
чтобы его магнитный момент
pm B , то есть к положению устойчивого
равновесия.
Можно показать, что этот вывод
справедлив для любого плоского витка.
Рассмотрим плоский контур произвольной
формы. Представим его, как бесконечно
большое число прямоугольных контуров

11.

pm
I
M
B const
B
dl1
d l2
M i IS i B sin
величина вращательного момента,
действующего на один из контуров
На весь плоский контур действует момент
N
N
N
i 1
i 1
i 1
IB
sin
S
IS
B
sin
M
i
M i
i
IB sin S pm B sin

12.

При повороте контура на угол dα
совершена работа
d A d WM M d pm B sin d
Потенциальная энергия контура с током
в однородном магнитном поле
при повороте контура на угол
WM A
pm B sin d pm B cos ,
2
где
n, B

13.

pm B
WM
pm B
0
2
pm B
pm B
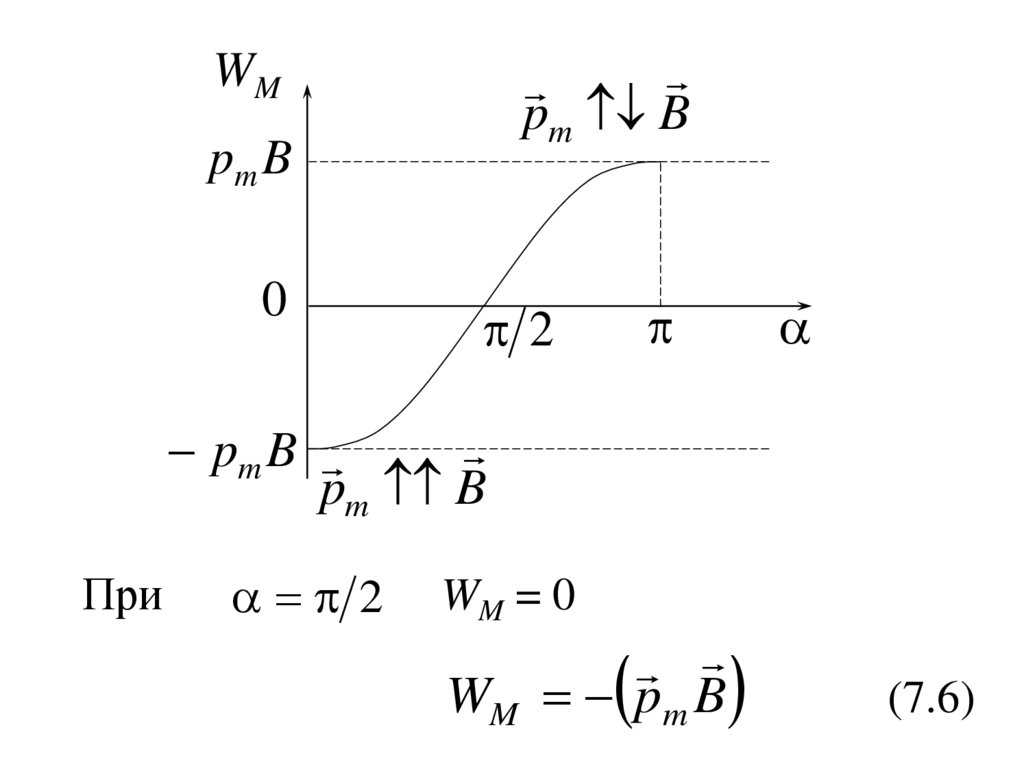
При
2
WM = 0
WM
pm B
(7.6)

14. Контур с током в неоднородном магнитном поле

Выражение (7.5) справедливо и для
неоднородных магнитных полей.
При достаточно малых размерах контура
с током (для элементарного контура с током –
выполняется) влиянием неоднородности
магнитного поля на вращающий момент
можно пренебречь.

15.

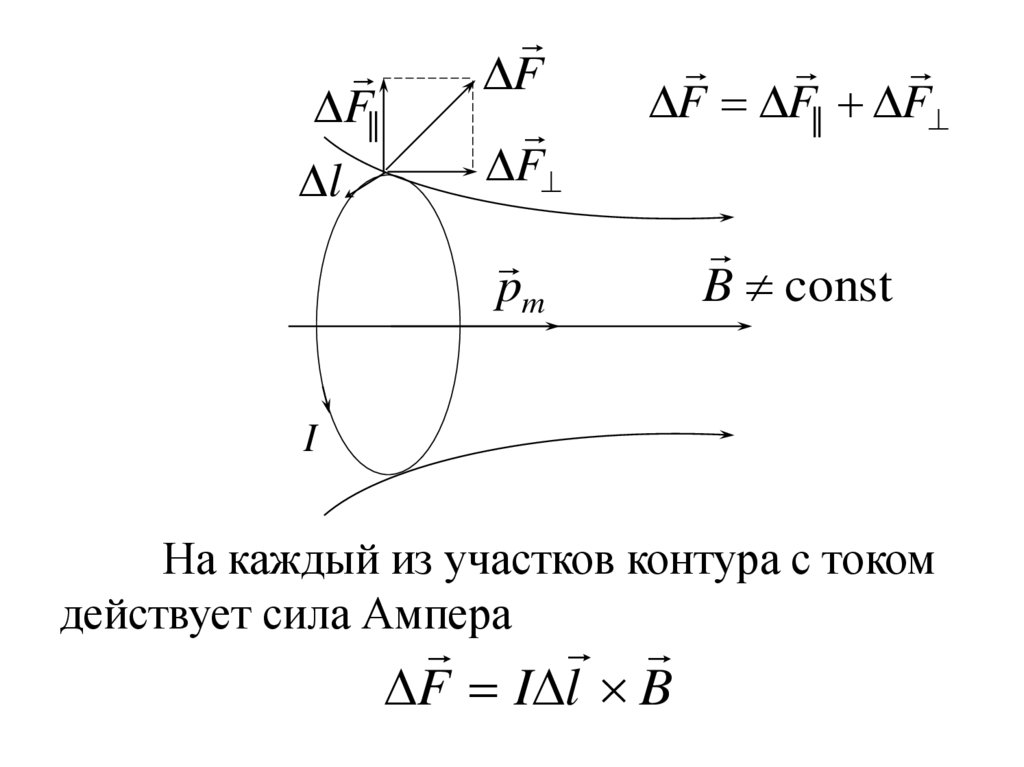
F||
l
F
F
F F|| F
pm
B const
I
На каждый из участков контура с током
действует сила Ампера
F I l B

16.

N
равнодействующая
i 1
d F
i
вызывает
перемещение
контура,
характеризуемого p m в магнитном поле.
Без вывода. Сила, втягивающая контур с
током в неоднородное магнитное поле
F pm B
(7.7)
Во внешнем неоднородном магнитном поле
элементарный контур с током будет
поворачиваться к положению устойчивого
равновесия и втягиваться в область более
сильного поля.

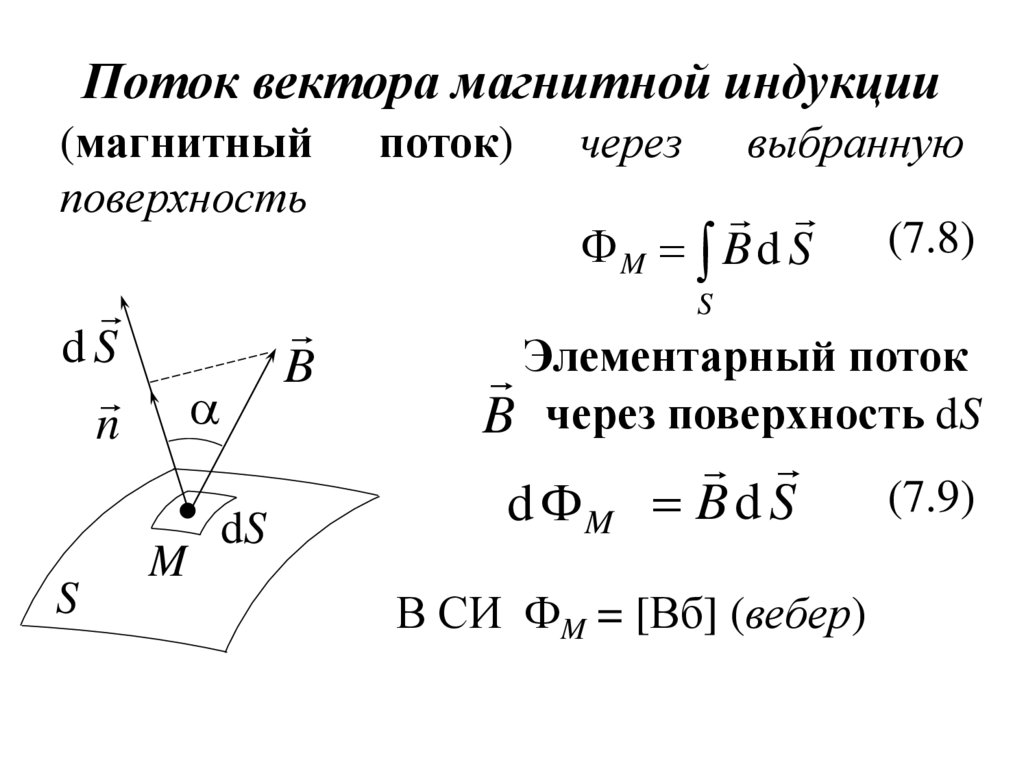
17. Поток вектора магнитной индукции

(магнитный
поверхность
dS
n
S
M
dS
B
поток)
через
выбранную
(7.8)
M B d S
S
Элементарный поток
B через поверхность dS
(7.9)
d M B d S
В СИ ФM = [Вб] (вебер)

18.

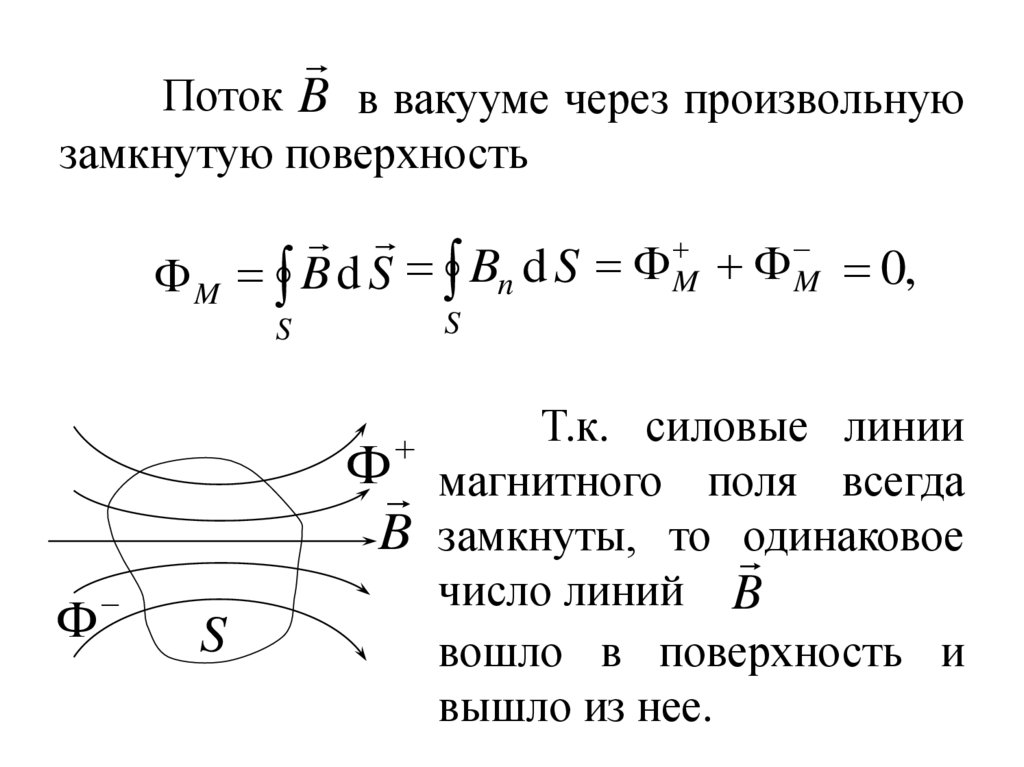
Поток B в вакууме через произвольную
замкнутую поверхность
M B d S Bn d S M M 0,
S
S
Т.к. силовые линии
магнитного поля всегда
B замкнуты, то одинаковое
число линий B
вошло в поверхность и
вышло из нее.
S

19. Теорема Гаусса для магнитного поля

Интегральная форма. Поток вектора
магнитной индукции
через замкнутую
поверхность равен нулю
Bd S 0
(7.10)
S
0
div
Bd
V
B
d
S
S
V
Дифференциальная форма
div B 0
(7.11)

20.

Физический смысл: (7.10) – в природе
отсутствуют магнитные заряды; (7.11) –
силовые линии магнитного поля (линии
магнитной индукции) не имеют ни
источников, ни стоков, т.е. они замкнуты.

21. Работа по перемещению проводника с током в магнитном поле

B const
I
l
I
F
dx
На подвижную перемычку действует
сила Ампера
F IlB

22.

Работа силы Ампера
A F d x IlB d x IB d S I d ,
где dS – приращение площади, ограниченной
контуром.
В случае произвольного направления поля B
A F d x cos
B
n
IlB cos d x
I
l
dx
F
IB d S cos
IBn d S I d

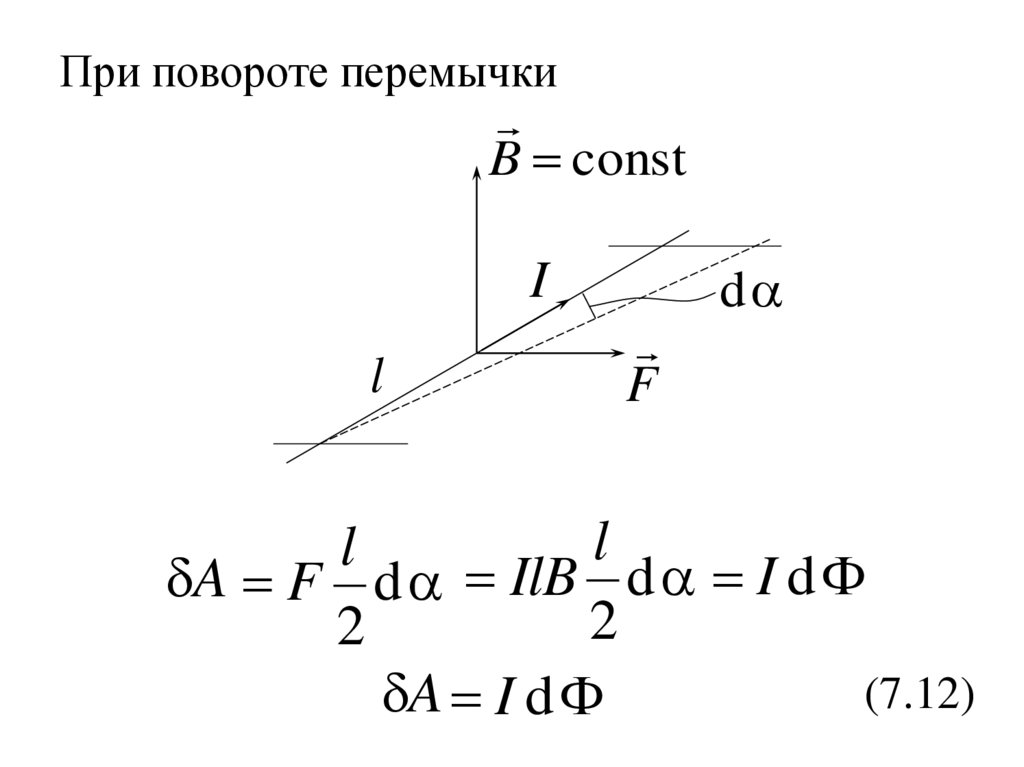
23. При повороте перемычки

B const
I
l
F
d
l
l
A F d IlB d I d
2
2
(7.12)
A I d

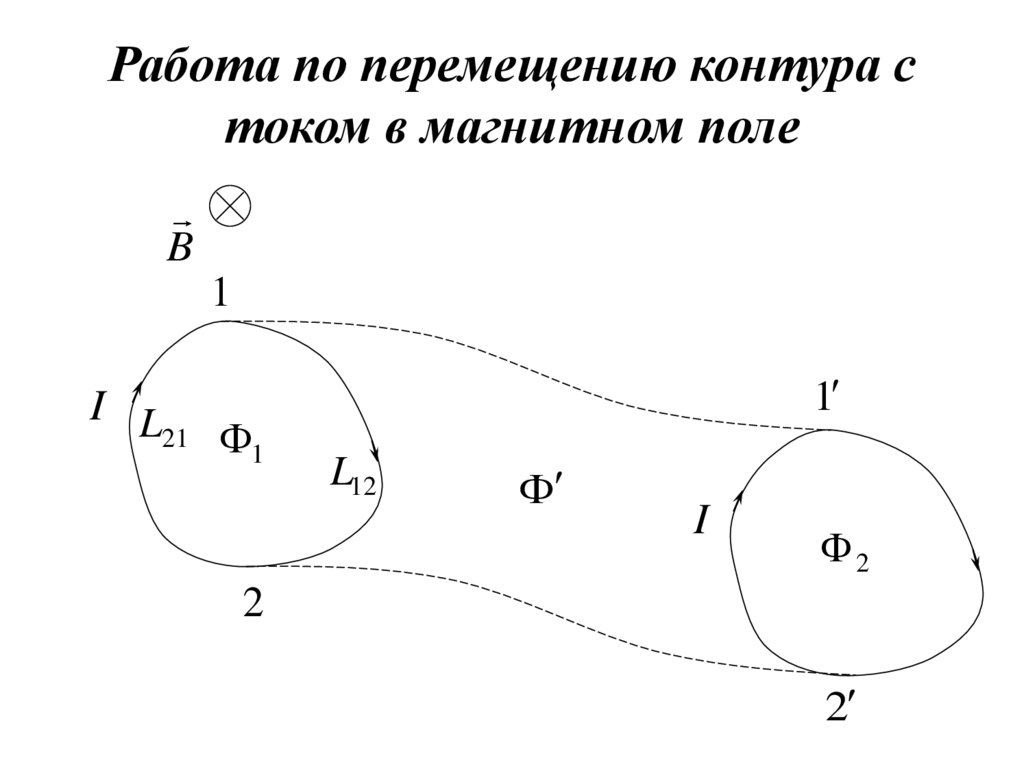
24. Работа по перемещению контура с током в магнитном поле

B
1
I L
21
1
1
L12
I
2
2
2

25.

Работа по перемещению части контура L12
AL12 I 2
Работа по перемещению части контура L21
AL21 I 1
Работа по перемещению всего контура с
током I в магнитном поле
A AL12 AL21 I 2 I 1
I 2 1 I

26.

Работа амперовых сил при полном
перемещении контура с током от начального
положения 1 до конечного 2:
2
A I d
(7.13)
1
Если при этом перемещении ток через контур
поддерживать постоянным (I = const), то:
A I 2 1 I
(7.14)
где Φ1 и Φ2 - магнитные потоки сквозь контур
в его начальном и конечном положениях.