Взаимодействие магнитного поля и проводников с током

1. ЭЛЕКТРОМАГНЕТИЗМ

Лекция «Взаимодействие
магнитного поля и проводников с
током»

2. Закон Ампера

На элемент проводника dl с током I в магнитном поле
действует сила (Ампера)
dFA I dl B
где dl – вектор, по модулю равный dl и совпадающий с
направлением тока в проводнике.
Сила Ампера по модулю:
dFA BIdl sin
где – угол между направлением тока в проводнике и
вектором магнитной индукции.

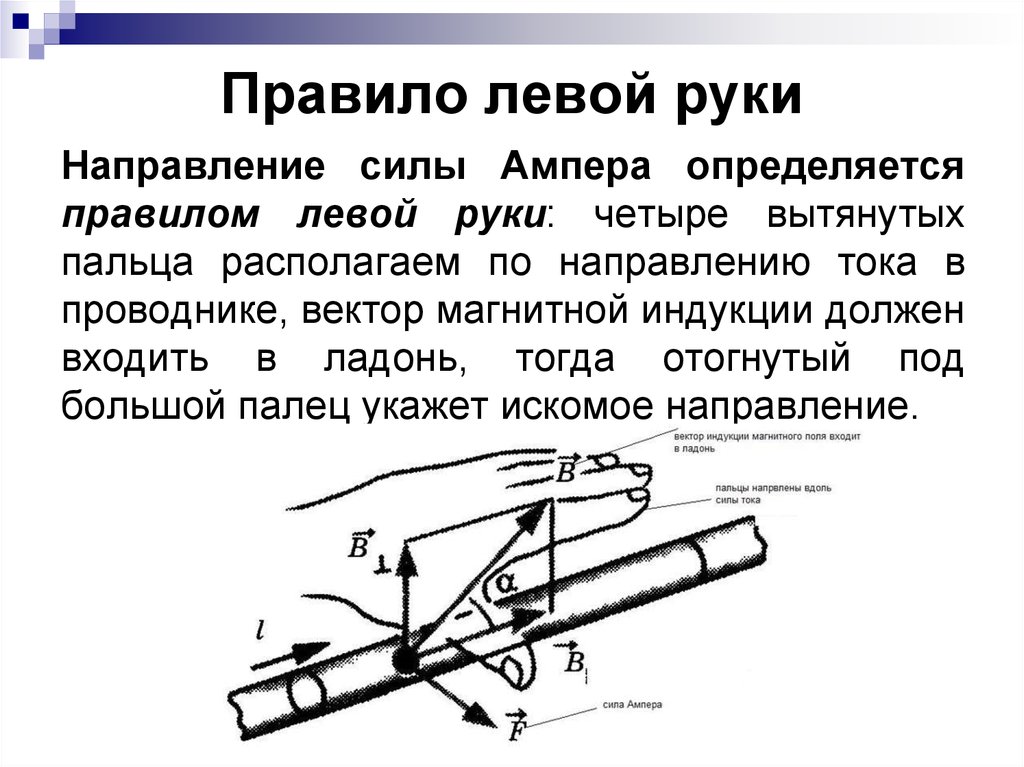
3. Правило левой руки

Направление силы Ампера определяется
правилом левой руки: четыре вытянутых
пальца располагаем по направлению тока в
проводнике, вектор магнитной индукции должен
входить в ладонь, тогда отогнутый под
большой палец укажет искомое направление.

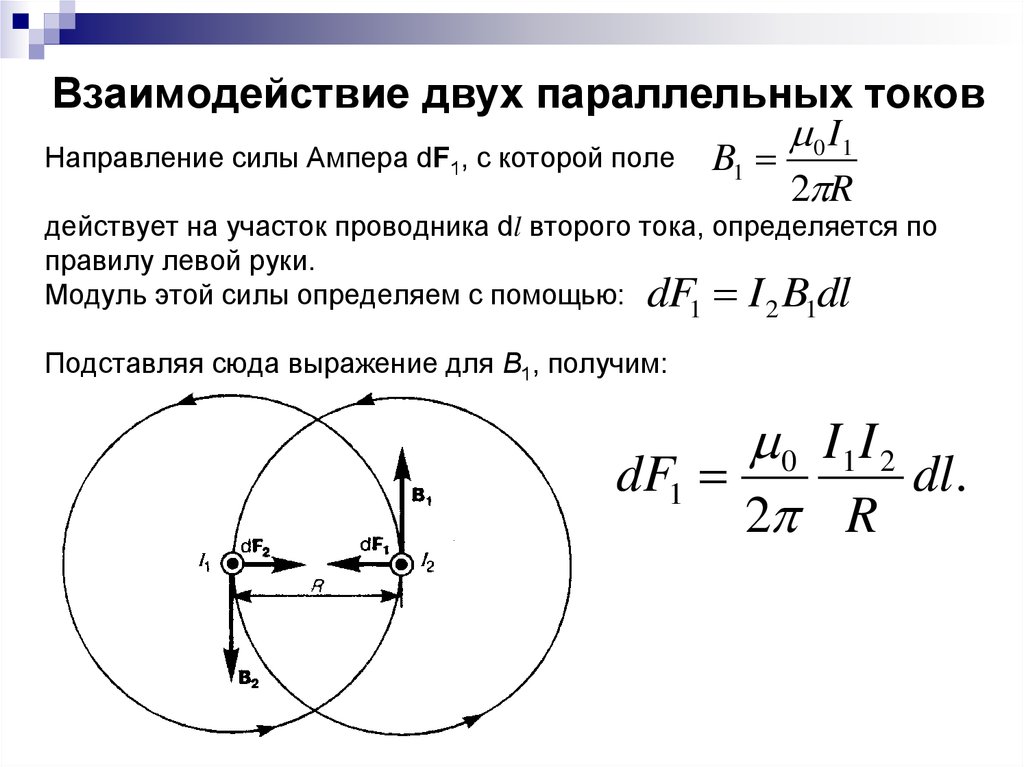
4. Взаимодействие двух параллельных токов

0 I1
Направление силы Ампера dF1, с которой поле B1
2 R
действует на участок проводника dl второго тока, определяется по
правилу левой руки.
Модуль этой силы определяем с помощью: dF1 I 2 B1dl
Подставляя сюда выражение для В1, получим:
0 I1 I 2
dF1
dl.
2 R

5. Взаимодействие двух параллельных токов

Рассуждая аналогично, можно показать, что сила dF2, с которой
магнитное поле тока I2 действует на участок dl проводника с током I1,
направлена в противоположную сторону и по модулю равна
0 I1 I 2
dF2 I1 B2 dl
dl.
2 R
Вывод.
Два
параллельных
тока
одинакового
направления притягиваются друг к другу с силой
0 I1 I 2
dF
dl.
2 R
Если токи имеют противоположные направления, то,
используя правило левой руки, можно показать, что между
ними действует сила отталкивания.

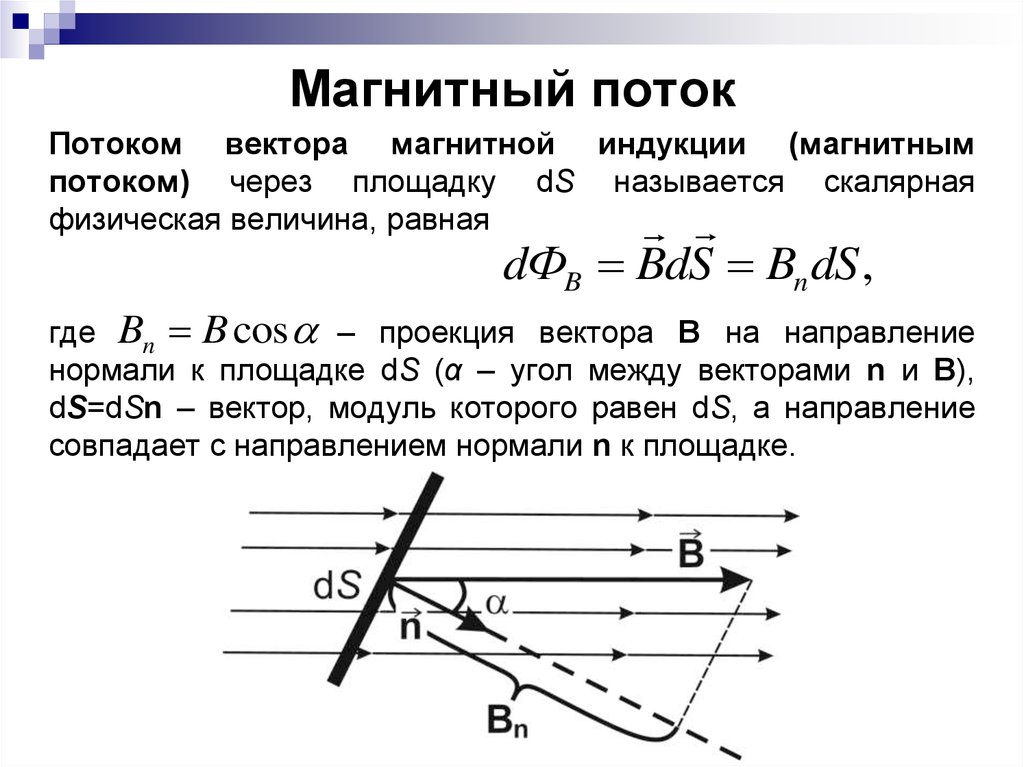
6. Магнитный поток

Потоком вектора магнитной индукции (магнитным
потоком) через площадку dS называется скалярная
физическая величина, равная
dФB BdS Bn dS ,
где Bn B cos – проекция вектора В на направление
нормали к площадке dS (α – угол между векторами n и B),
dS=dSn – вектор, модуль которого равен dS, а направление
совпадает с направлением нормали n к площадке.

7. Магнитный поток

Поток вектора магнитной индукции через произвольную
поверхность S равен
ФB BdS Bn dS .
S
S
Для однородного поля и плоской поверхности,
расположенной перпендикулярно вектору В, Bn=B=const:
ФВ=BS.
[Вб]
Отсюда определяют единицу магнитного потока – вебер.
Теорема Гаусса для поля В: поток вектора магнитной
индукции сквозь любую замкнутую поверхность равен
нулю:
BdS B dS 0.
n
S
S

8. Рамка с током в магнитном поле

На каждую сторону контура действует сила Ампера. На
горизонтальные стороны l контура действуют силы, которые
растягивают (сжимают) контур, не поворачивая его. На каждую
из вертикальных сторон а действует сила Ампера FA=BIa. Эти
силы создают пару сил, момент которой равен
M Fl cos BIal cos .
Момент сил (вращающий
момент)
стремится
повернуть рамку так, чтобы
поток dФВ вектора В был
максимальным.

9. Магнитный момент контура с током

Величина, называемая магнитным моментом контура:
pm IS ISn,
где S – площадь контура с током I, n – нормаль к плоскости
рамки. Положительное направление нормали совпадает с
направлением перемещения буравчика с правой нарезкой,
вращаемого в направлении тока.
Установлено, что отношение максимального вращающего
момента Mmax, действующего на контур, к магнитному моменту
контура pm для произвольно выбранной точки есть величина
постоянная, не зависящая от свойств контура. Эту величину и
называют магнитной индукцией:
M max
B .
pm

10. Благодарю за внимание