Уравнение Эйлера

1.

Самарский государственный аэрокосмический университет
Лекция 2.
Уравнение Эйлера
О. Л. Старинова
Кафедра Динамики полета и систем управления
2020 г.

2.

Сильный и слабый экстремум
1
y
C
Функционал J(y),
a,b достигает при y y0
слабого экстремума, если 0 , такое что J(y)- J(y0)
сохраняет знак при всех y y0 C .
1
Функционал J(y), y C a, b достигает при y y0
сильного экстремума, если 0 , такое что J(y)- J(y0)
сохраняет знак при всех y y0 C .

3.

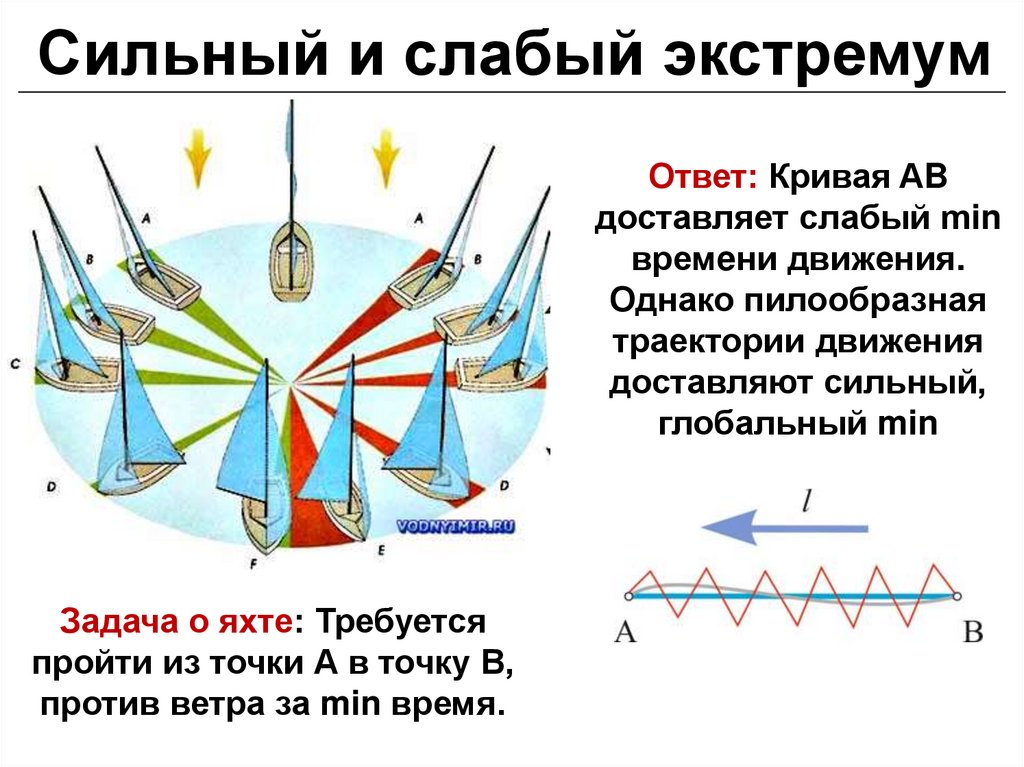
Сильный и слабый экстремум
Ответ: Кривая AB
доставляет слабый min
времeни движения.
Однако пилообразная
траектории движения
доставляют сильный,
глобальный min
Задача о яхте: Требуется
пройти из точки А в точку В,
против ветра за min время.

4.

Необходимое условие экстремума
Th 2.1 Для того, чтобы функционал J(y) при y y0
Курс
достигал экстремума, необходимо, чтобы его вариация
вариационные
методы
(если она существует)
обращалась
в ноль J 0 (2.1)
Рассмотрим для определенности минимум:
J J y0 x y J y0 x 0
для всех достаточно малых y .
(2.2)
По определению вариации
(2.3)
J J y0 x , y о y0 x , y y
Знак выражения (2.3) определяется знаком J .
Но J - линейный функционал, поэтому
J y0 x , y J y0 x , y . Тогда если J 0
выражение (2.3) может быть, как положительным, так и
отрицательным, т.е. экстремум в данном случае
невозможен. Поэтому J 0

5.

Первая вариация
интегрального функционала
Рассмотрим интегральный функционал
x2
J y F x, y, y ' dx extr
(2.4)
x1
В этом случае вариация J(y) вызывается изменением
(вариацией) функции y(x) и её производной y’(x):
(2.5)
y x y x y x ,
y x y x y x
0
0
Вычислим вариацию функционала как линейную часть его
приращения. Для этого разложим F(x, y0+ y0, y 0+ y ) в ряд
Тейлора в окрестности экстремальной функции y0 с
удержанием только линейных членов, а затем
проинтегрируем по частям:

6.

Первая вариация
интегрального функционала
J y0
x2
F x, y
0
y, y '0 y ' F x, y0 , y '0 dx
x1
F
F
F x, y0 , y '0
y
y F x, y0 , y '0 dx
y
y
x1
x2
dFy
u Fy , du
dx
Fy y Fy ' y ' dx
dx
x1
dv y ' dx, v y
x2
x2
Fy ydx Fy ' y
x2
x1
x1
Fy ' y x
x2
1
x2
x1
dFy '
dx
ydx
dFy '
ydx
Fy
dx
x1
x2
(2.6)

7.

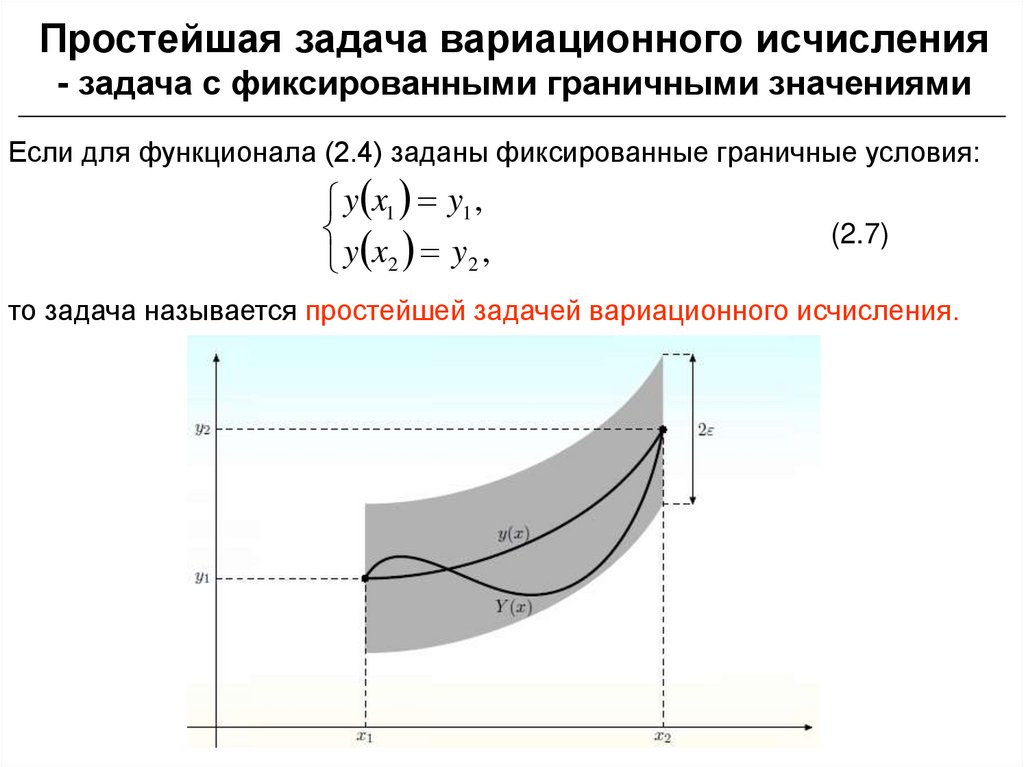
Простейшая задача вариационного исчисления
- задача с фиксированными граничными значениями
Если для функционала (2.4) заданы фиксированные граничные условия:
y x1 y1 ,
y x2 y 2 ,
(2.7)
то задача называется простейшей задачей вариационного исчисления.

8.

Простейшая задача вариационного исчисления.
Дифференциальное уравнение Эйлера
Согласно необходимому условию экстремума (2.1),
формуле для первой вариации функционала (2.6) и
граничным условиям (2.7), экстремум функционала (2.4)
достигается при выполнении следующих условий:
y x1 y x2 0
Fy
dFy '
dx
0
(2.8)
(2.9)
Уравнение (2.9) называется уравнением Эйлера.
Экстремалью называется интегральная кривая
(решение) дифференциального уравнения Эйлера.
Все экстремали одной задачи образуют поле
экстремалей.

9.

Пример 2.1 Решение дифференциального
уравнения Эйлера.
Найти экстремаль функционала
y 1 1;
J y x 2 y 2 y '2 dx;
y 1 2.
1
1
Запишем уравнение Эйлера для этого функционала.
F
2 y,
y
F
2 y ,
y
2 y 2 y 0
d F
2 y
dx y
y ' ' y 0
Соответствующее характеристическое уравнение и его
корни:
k1, 2 1
k2 1 0

10.

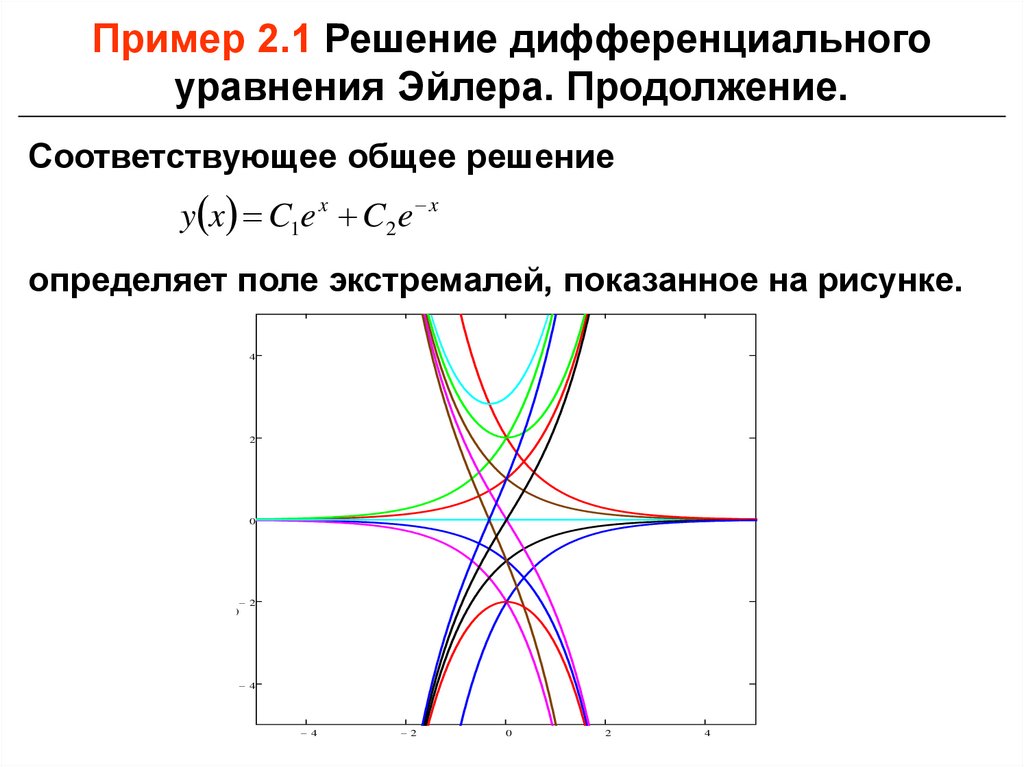
Пример 2.1 Решение дифференциального
уравнения Эйлера. Продолжение.
Соответствующее общее решение
y x C1e x C2 e x
определяет поле экстремалей, показанное на рисунке.
5
y( x , 1 , 0)
y( x , 1 , 0)
4
y( x , 2 , 0)
y( x , 2 , 0)
y( x , 0 , 0)
2
y( x , 0 , 1)
y( x , 0 , 1)
y( x , 0 , 2)
y( x , 0 , 2)
y( x , 1 , 1)
0
y( x , 1 , 1)
y( x , 2 , 1)
y( x , 2 , 1)
y( x , 1 , 1)
y( x , 1 , 1)
2
y( x , 2 , 1)
4
5
4
5
2
0
x
2
4
5

11.

Пример 2.1 Решение дифференциального
уравнения Эйлера. Продолжение.
Найдем произвольные постоянные, обеспечивающие
выполнение граничных условий:
1 C1e 1 C2 e1
2 C1e1 C2 e 1
Определяем
произвольные
постоянные в
MathCad:

12.

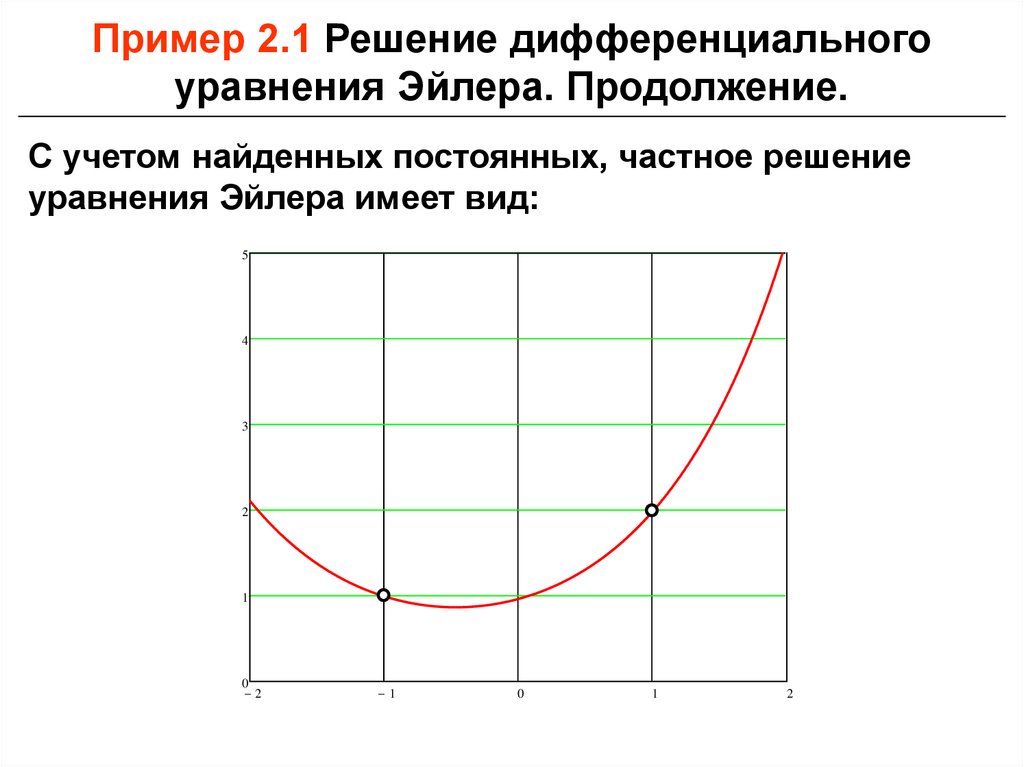
Пример 2.1 Решение дифференциального
уравнения Эйлера. Продолжение.
С учетом найденных постоянных, частное решение
уравнения Эйлера имеет вид:
5
5
4
3
y( x , 0.699 , 0.273)
2
1
0
0
2
2
1
0
x
2
1
2

13.

Частные случаи уравнения Эйлера
Распишем уравнение Эйлера более подробно:
F
d F
0
y dx y
F x, y, y F dx F dy F dy
0
y
x y dx y y dx y y dx
F
F F
F
y
y 0
y x y y y
y y
(2.10)
Утверждение 1. Если подынтегральная функция
не зависит от y, то уравнение Эйлера примет вид:
F
d F
C
0 или
y
dx y
(2.11)

14.

Пример 2.2 Подынтегральная функция
не зависит от у
Найти экстремаль функционала
2
J y
1
1 y 2 dx
x
, y 1 0 , y 2 1
Согласно (2.11)
y
y 2 1 x 2C 2 C 2 x 2
C
x 1 y 2
Cx
y
Т.е.
, следовательно
1 C 2x 2
y
Cx
1
dx
1 C 2 x 2 C1
C
1 C 2x 2

15.

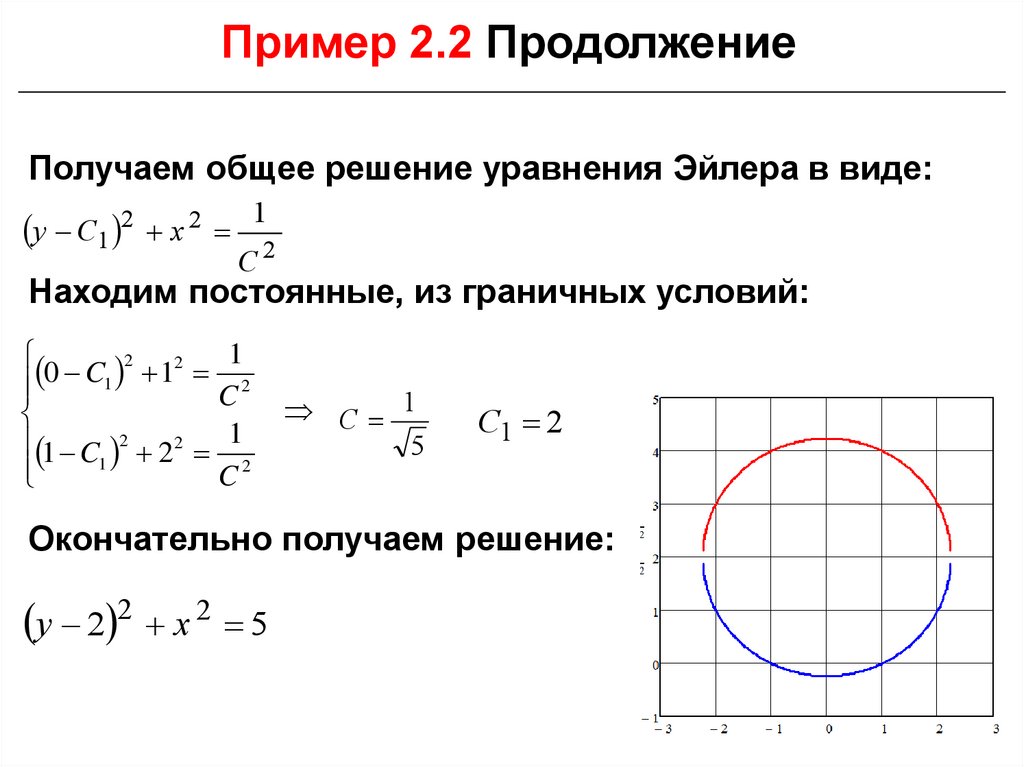
Пример 2.2 Продолжение
Получаем общее решение уравнения Эйлера в виде:
y C1 2 x 2
1
C2
Находим постоянные, из граничных условий:
1
2
2
0 C1 1 2
C
1 C 2 2 2 1
1
C2
C 1
5
C1 2
Окончательно получаем решение:
y 2 2 x 2 5

16.

2. Подынтегральная функция не зависит от x
Утверждение 2. В этом случае, по формуле (2.10)
J
F F
F
y
y 0
y y y
y y
Умножив это уравнение на y получим:
F
F
F
2
y y 0
y
y
y
y y
y y
F F
F
F
F
F
2
y y 0
y
y
y
y
x y
y
y
y y
y y
d
F
F y
0
dx
y
F
F y
С
y
(2.12)

17.

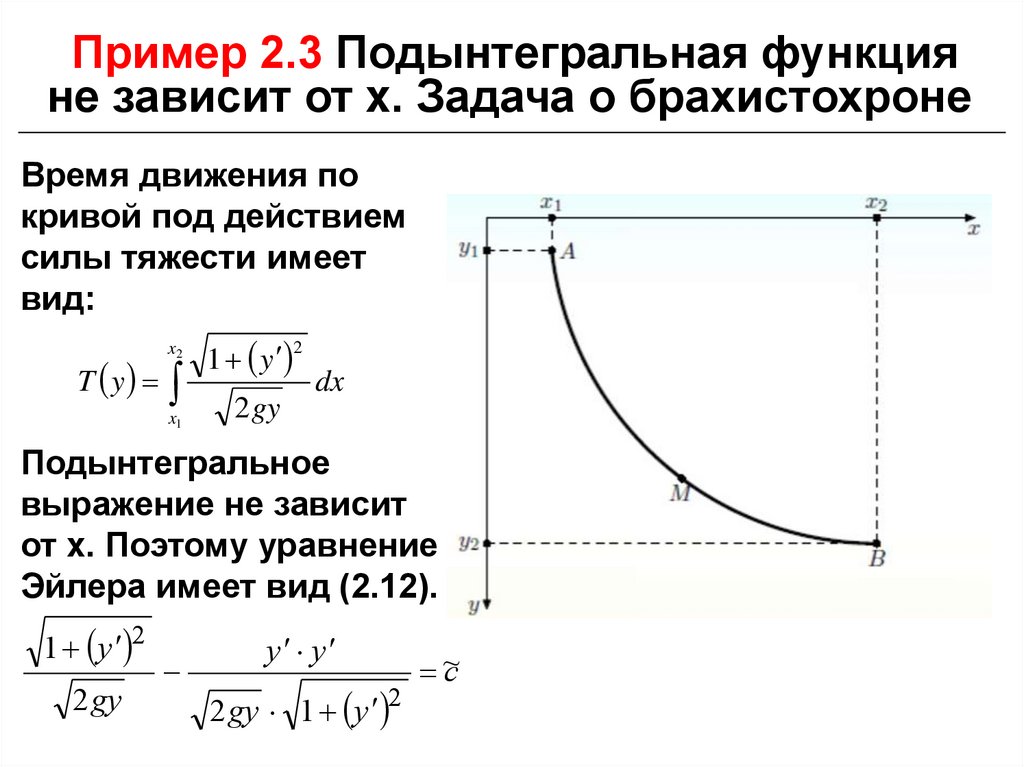
Пример 2.3 Подынтегральная функция
не зависит от x. Задача о брахистохроне
Время движения по
кривой под действием
силы тяжести имеет
вид:
T y
x2
x1
1 y
2
2 gy
dx
Подынтегральное
выражение не зависит
от x. Поэтому уравнение
Эйлера имеет вид (2.12).
1 y 2
2 gy
y y
2 gy 1 y 2
~c

18.

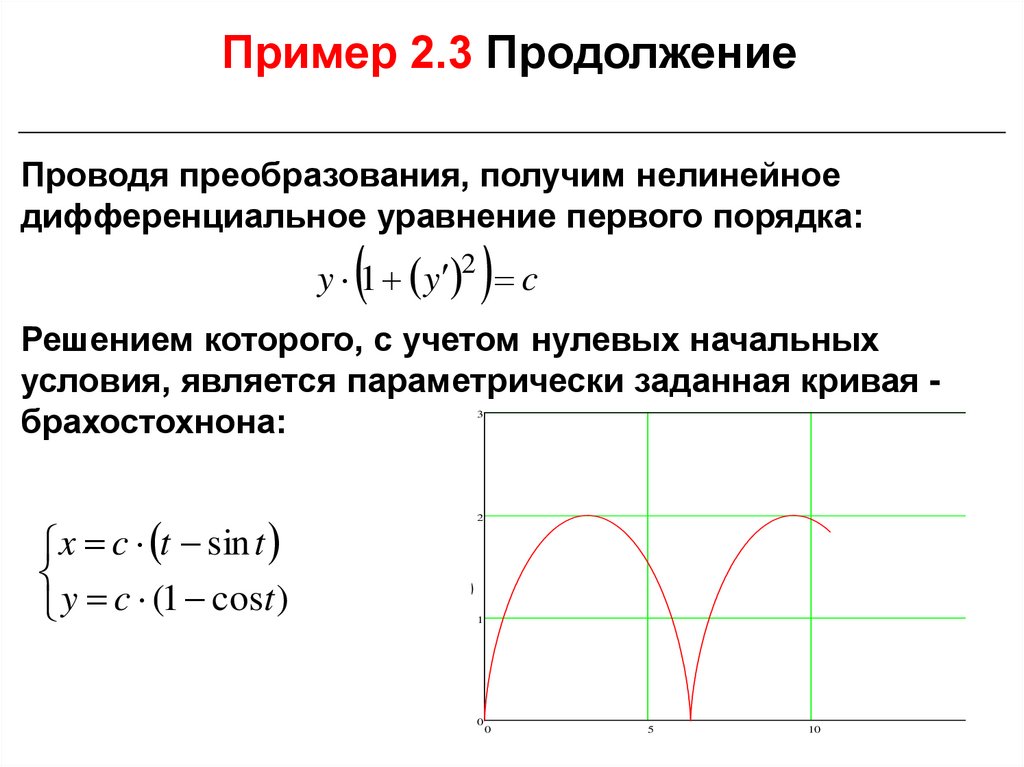
Пример 2.3 Продолжение
Проводя преобразования, получим нелинейное
дифференциальное уравнение первого порядка:
y 1 y 2 c
Решением которого, с учетом нулевых начальных
условия, является параметрически заданная кривая брахостохнона:
3
3
x c t sin t
y c (1 cost )
2
1 1
cos ( t)
1
0
0
0
0
5
10
1 t
sin( t)
10.544

19.

3. Подынтегральная функция не зависит от y’
В этом случае уравнение Эйлера обращается в
алгебраическое уравнение, задающее одну кривую.
F x, y
y
d F
0
dx y
F x, y
y
0
F1 x, y 0
В этом случае в решении нет произвольных
постоянных и оно может не удовлетворять граничным
условиям.
Поэтому, если граничные условия выполняются, то
получена экстремаль, если нет, то нет и решений у
данной вариационной задачи c заданными граничными
условиями.

20.

Лабораторная работа № 2
Простейшая задача вариационного исчисления.
Частные случаи решения уравнения Эйлера.
1. Для своего варианта функционалов a), b), c) найти
поле экстремалей в виде функции с двумя
произвольными постоянными.
2. Найти постоянные, обеспечивающие выполнение
граничных условий. Построить экстремали,
удовлетворяющие граничным условиям.
3. Вычислить значения функционалов на этих
экстремалях и при небольшом изменении функции.
Определить максимум или минимум доставляют
функционалу найденные экстремали.
4. Оформить отчет.