«Динамика». Динамика точки и механической системы

1. Теоретическая механика

Раздел
«Динамика»
Динамика точки и
механической системы

2.

Динамика точки

3.

Динамика – это раздел ТМ, в котором
изучаются
законы
движения
материальных тел под действием сил.
Сила – векторная мера взаимодействия тел.
В динамике силы – переменные.
Силы могут зависеть от:
- времени F f (t ),
- положения тела F f ( x) ,
- скорости F f (v).

4.

Инертность представляет собой свойство
материальных тел быстрее или медленнее
изменять скорость своего движения под
действием приложенных сил.
Масса – мера инертности тела. Она зависит
от количества вещества и считается
величиной постоянной.

5.

Законы механики Галилея–Ньютона.
1. Закон инерции. Материальная точка
сохраняет
состояние
покоя
или
равномерного прямолинейного движения,
пока действие других тел не изменит этого
состояния.
Точка, на которую не действуют никакие силы со
стороны других тел, называется изолированной.
Система отсчета, по отношению к которой
выполняется закон инерции, называется
инерциальной системой отсчета.

6.

2. Основной закон динамики. Ускорение
материальной
точки
пропорционально
приложенной силе и имеет одинаковое с ней
направление.
ma F

7.

3.
Закон
равенства
действия
и
противодействия. Силы взаимодействия
двух материальных точек равны по
величине
и
противоположны
по
направлению.
F1 F2

8.

4. Закон независимости сил (Закон
суперпозиции). Несколько одновременно
действующих на точку сил сообщают точке
такое ускорение, какое сообщила бы их
равнодействующая.
ma
n
Fk
k 1

9.

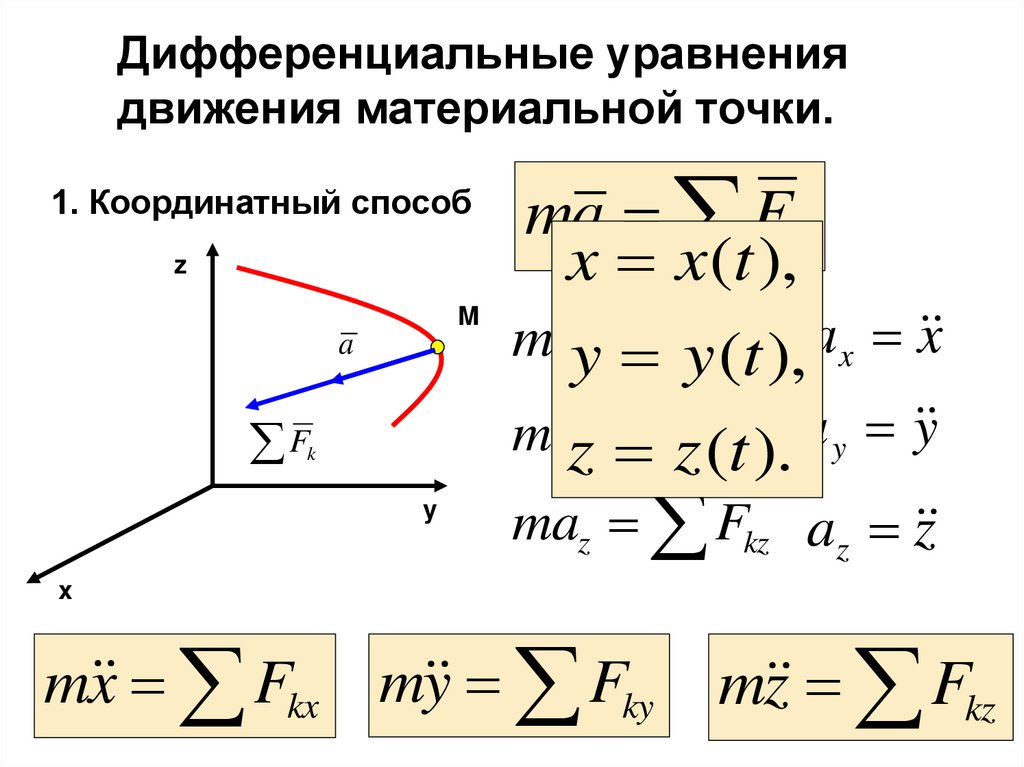
Дифференциальные уравнения
движения материальной точки.
1. Координатный способ
z
M
a
F
k
y
ma Fk
x x (t ),
a
x
mayx
F
x
y (tkx),
a
y
mazy
F
y
z (tky).
maz Fkz az z
x
m x Fkx m y Fky
m z Fkz

10.

r r (t )
2. Векторный способ
z
F
M
a
k
r
y
x
ma Fk
a r
mr Fk

11.

s s (t )
3. Естественный способ
F
a
ma Fk
M
k
n
ma Fk
ma
n
m s Fk
Fkn
a s
2
2
v
s
an
m 2
s Fkn

12.

Задачи динамики точки.
Первая задача динамики точки (прямая
задача): по заданному закону движения
определить силы, действующие на точку.
ma F
Первая задача динамики точки решается
дифференцированием закона движения
точки.

13.

Вторая задача динамики точки (обратная
задача): по заданным силам, действующим
на точку, определить закон ее движения.
ma F
В обратной задаче динамики решение сводится к
интегрированию дифференциальных уравнений движения.
Первый интеграл дает закон изменения скорости.
Второй интеграл – закон движения.
При решении второй задачи динамики надо задавать так
называемые начальные условия
t0 0; x0 , y0 , z0 ; x 0 , y 0 , z 0

14.

Динамика
механической системы

15.

1. Введение в динамику механической системы
Механическая
система
–
совокупность
абсолютно твердых тел или абсолютно твердых
тел и материальных точек, движения которых
взаимосвязаны.
Классификация сил, действующих на мех-ую систему:
-силы активные и реакции связей;
-силы внешние и внутренние.

16.

Внешние силы
e
Fk
действуют на систему со стороны других
тел, не входящих в эту систему.
Внутренние силы
i
Fk
силы взаимодействия между точками
одной и той же системы.

17.

Свойства внутренних сил в неизменяемой
механической системе:
1) Главный вектор внутренних сил в системе равен нулю.
Т.к. внутренние силы – это силы взаимодействия между
каждыми двумя точками системы, то они попарно равны и
противоположно направлены (согласно закону о действии и
противодействии)
n
F
k 1
i
k
0
2) Главный момент внутренних сил равен нулю
относительно любого центра и любой оси
M F 0
n
k 1
A
i
k
M F 0
n
k 1
x
i
k

18.

3) Сумма работ внутренних сил равна нулю на любом
возможном перемещении.
n
i
А
F
k k 0
k 1
Неизменяемая механическая система – это механическая
система, в которой расстояние между двумя
взаимодействующими точками во все время движения
остается постоянным.

19.

2. Масса системы. Центр масс.
Масса системы равна арифметической сумме масс всех точек
или тел, образующих систему.
M mk
Центром масс механической системы называется
радиус-вектор которой определяется выражением:
1
rC
M
точка,
mk rk
Координаты центра масс:
xC
1
M
mk xk ;
yC
1
M
mk yk ;
1
zC
M
m z
k k
Центр масс характеризует распределение масс в системе.

20.

3. Момент инерции тела относительно оси. Радиус инерции.
Моментом инерции тела (системы) относительно данной
оси Oz (или осевым моментом инерции) называется
скалярная величина, равная сумме произведений масс всех
точек тела (системы) на квадраты их расстояний от этой оси
I z mk rk
2
Радиусом инерции тела относительно оси Оz называется
линейная величина i определяемая равенством
I z Mi
2
z
Радиус инерции геометрически равен расстоянию от оси Оz до
той точки, в которой надо сосредоточить массу всего тела, чтобы
момент инерции одной этой точки был равен моменту инерции
всего тела.

21.

4. Дифференциальные уравнения движения механической
системы
e i
mk ak Fk Fk .
Полностью описывает движение механической
системы.
Следовательно, для всей системы будет:
Для решения многих задач динамики вместо непосредственного
интегрирования дифференциальных уравнений движения
оказывается
более
эффективным
пользоваться
так
называемыми общими теоремами, которые являются
следствием основного закона динамики.

22.

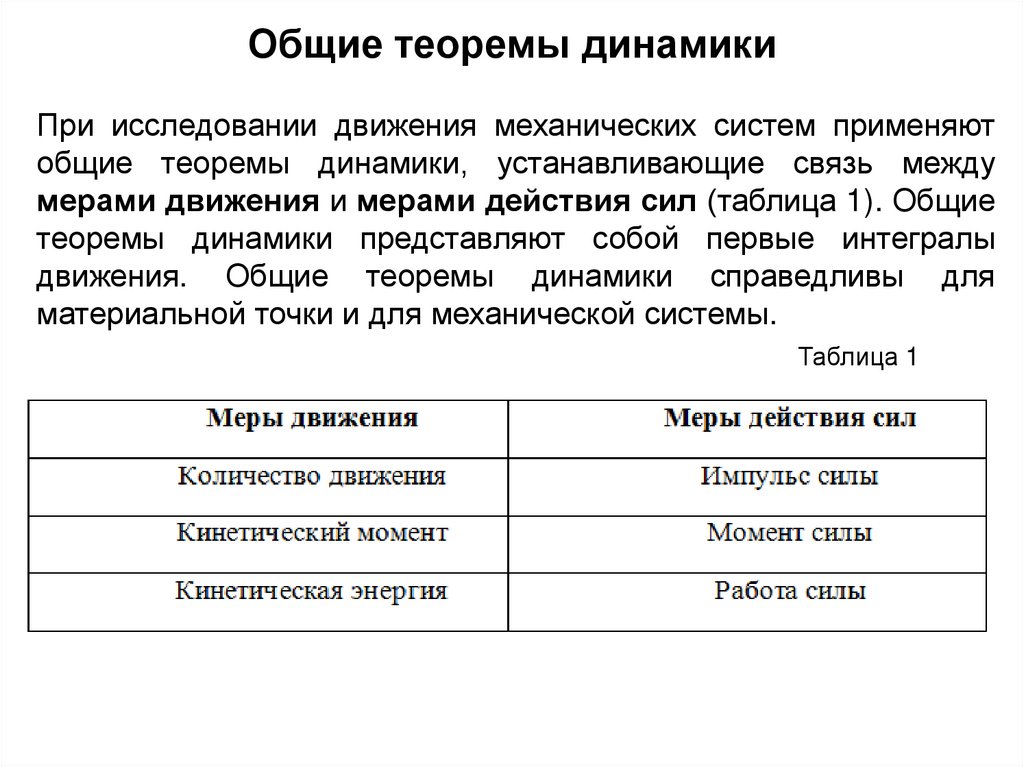
Общие теоремы динамики
При исследовании движения механических систем применяют
общие теоремы динамики, устанавливающие связь между
мерами движения и мерами действия сил (таблица 1). Общие
теоремы динамики представляют собой первые интегралы
движения. Общие теоремы динамики справедливы для
материальной точки и для механической системы.
Таблица 1

23.

5. Теорема об изменении количества движения
механической системы.
Количество движения материальной точки – вектор, численно
равный произведению массы точки на ее скорость
м
q mv кг ; Н с
с
Количество движения является мерой механического движения.
Вектор количества движения имеет направление скорости и приложен к
точке.
m
v
mv
Количество движения механической системы – вектор, численно равный
главному вектору количеств движения всех точек системы
Q
n
mk vk
k 1

24.

Импульс силы характеризует действие силы на точку в
течение некоторого времени.
Элементарный импульс силы:
ds Fdt
Направлен элементарный импульс по линии действия силы.
Полный импульс силы определяют как интеграл за
время действия силы:
.
S F dt Н с
0
Импульс силы за любой промежуток времени τ равен
определенному интегралу от элементарного импульса,
взятому в пределах от 0 до τ.

25.

Теорема об изменении количества движения.
1. Дифференциальная форма. Производная от количества
движения механической системы по времени равна главному
вектору всех внешних сил, действующих на систему
dQ
dt
Fke
Главный вектор внутренних сил равен нулю по свойству внутренних сил.
2. Интегральная форма. Изменение количества движения
системы за некоторый промежуток времени равно векторной
сумме всех импульсов внешних сил, действующих на систему
Q Q0
e
Sk
Векторная сумма всех импульсов внутренних сил равна нулю, так как
главный вектор внутренних сил равен нулю по свойству внутренних сил.

26.

Законы сохранения количества движения системы
являются следствиями из теоремы об изменении
количества движения.
1. Если главный вектор внешних сил равен нулю, то количество
движения системы постоянно по величине и направлению:
F
e
k
0 Q const
dQ
0 Q const
dt
2. Если проекция главного вектора внешних сил на какую-либо ось
(например, на ось x) равна нулю, то проекция вектора количества
движения системы на эту же ось постоянна:
e
F
kx 0 Qx const
Внутренние силы изменить суммарное количество движения системы
не могут.

27.

Количество движения системы можно
рассматривать как характеристику
поступательного движения системы, а при
сложном движении – как характеристику
поступательной части движения вместе с
центром масс.

28.

6. Дифференциальные
движения.
уравнения
поступательного
Если механическая система представляет собой твердое тело, то при
поступательном движении скорости и ускорения всех точек в данный
момент времени будут иметь одинаковые по модулю и направлению
ускорения.
dQ
dt
dvC
a
dt
dvC
dQ d
( mk * vC ) M
dt dt
dt
Fke
Дифференциальное уравнение движения твердого тела в векторной форме
имеет вид:
Ma
n
n
Fke
т.к.
a r
M r Fke
, то
k 1
k 1
где
M
n
n
k 1
mk
– масса системы,
k 1
Fke
– главный вектор внешних сил.

29.

7. Теорема об изменении момента количества движения
механической системы.
Моментом количества движения материальной точки
массой m, движущейся со скоростью v, относительно
какого-либо центра O называют момент вектора
количества движения этой точки относительно этого
центра.
м кг м 2
LO M O mv r q м кг ;
с с
Модуль вектора
LO : LO mvh
где h – плечо
Момент количества движения материальной точки
относительно оси является скалярной величиной.
Lz mvh
_
v
O
h
m
_
v
h
m

30.

Кинетический момент системы, состоящей из n точек,
относительно оси z равен геометрической сумме векторов
моментов количества движения всех точек системы
относительно этой оси:
n
n
n
k 1
k 1
k 1
Lz Lzk M z mk vk mk vk rk
Для абсолютно твердого тела, вращающегося вокруг
неподвижной оси, кинетический момент тела относительно этой
оси равен:
Lz mk vk rk mk rk2 mk rk2
vk rk
Iz -
осевой момент инерции
Lz I z

31.

Теорема об изменении кинетического момента.
Производная по времени от кинетического момента
механической системы относительно некоторого центра
(оси) равна главному моменту внешних сил, действующих
на систему, относительно этого же центра (этой же оси):
dLO
e
M Ok
dt
dLz
M zke
dt

32.

Законы сохранения кинетического момента системы
являются следствиями из теоремы об изменении
кинетического момента:
1. Если главный момент всех внешних сил системы относительно
некоторого центра равен нулю, то кинетический момент системы
относительно этого центра постоянен:
M
e
Ok
0 LO const
2. Если главный момент всех внешних сил системы относительно некоторой оси
равен нулю, то кинетический момент системы относительно этой оси постоянен:
M
e
zk
0 Lz const

33.

8. Дифференциальное уравнение вращательного движения.
Дифференциальное уравнение вращательного движения
выводят из теоремы об изменении кинетического момента:
dLz
M z Fke
dt
, где
Lz I z
Тогда это уравнение имеет вид:
I z
e
M z Fk
При вращательном движении осевой момент инерции является
мерой инертности (при поступательном движении мерой
инертности является масса).

34.

9. Теорема об изменении кинетической энергии
механической системы
Кинетическая энергия материальной точки – скалярная
положительная величина, равная половине произведения
массы точки на квадрат ее скорости:
mv2
2
кг м 2
2 ; Н м ; Дж
с
Кинетическая энергия механической системы определяется
как алгебраическая сумма кинетических энергий всех точек,
образующих эту систему:
mk vk2
2

35.

Кинетическая энергия твердого тела:
2
mvC
1) Поступательное движение –
2) Вращательное движение –
I z
2
2
2
3) Плоское движение –
mvC2 I zC 2
2
2
Кинетическая энергия тела равна нулю, если тело покоится.

36.

Работа силы.
Работа характеризует действие силы на некотором
перемещении точки ее положения (материальной точки или
точки твердого тела).
Работа постоянной силы (F=const)
A Fs cos
А>0, если 0
А=0, если
А<0, если
2
2
2
(острый угол)
(прямой угол)
(тупой угол)
Работа отрицательна, когда сила замедляет движение

37.

s1
Работа переменной силы, зависящей от перемещения –
Работа силы тяжести –
A
F (s)ds
s0
A GH
где H – величина вертикального перемещения.
Работа силы тяжести не зависит от вида траектории движения точки
или тела.
Работа силы упругости –
c 2
A x0 x12
2
x0 – начальная деформация пружины,
x1 – конечная деформация пружины.
Работа силы упругости отрицательна в том случае, когда деформация
увеличивается,т.е. когда сила упругости направлена противоположно
перемещению ее точки приложения, и положительна, когда
деформация уменьшается.

38.

Работа постоянной силы, приложенной к вращающемуся телу
A M O F
Работа пары сил с моментом
M const –
A M
Работа пары сил с моментом, зависящим от угла поворота –
1
A
0
M ( ) d

39.

Теорема об изменении кинетической энергии системы.
Дифференциал кинетической энергии системы равен сумме
элементарных работ всех внешних и внутренних сил,
действующих на систему (дифференциальная форма):
d
e
Ak
i
Ak
Изменение кинетической энергии системы на некотором
перемещении равно сумме работ всех внешних и внутренних
сил на этом перемещении (интегральная форма):
0
e
Ak
i
Ak
В неизменяемой механической системе сумма
внутренних сил на любом перемещении равна нулю.
работ