Похожие презентации:
Динамика механической системы
1.
Динамикамеханической
системы
2.
3.3.1. Общие положения.• Механической системой называется
любая совокупность материальных
точек, рассматриваемая при решении
конкретной задачи.
Примером механической системы может
служить солнечная система, твердое тело,
механизм и т.д.
Силы, действующие на точки системы,
подразделяются на внешние и внутренние.
3.
• Внешние - это силы взаимодействиямежду точками, входящими и не
входящими в систему.
Они обозначаются (индекс “е” - exteriorвнешний).
• Внутренние - это силы взаимодействия
между точками самой системы.
Обозначаются (“i” - interior- внутренний).
Разделение сил на внешние и внутренние
условно и зависит от выбора системы.
4.
Свойства внутренних сил:• 1.Сумма всех внутренних сил
системы равна нулю.
• 2.Сумма моментов всех внутренних
сил системы относительно любой
точки или оси равна нулю.
5.
• Если выделить две точки системы ипоказать силы взаимодействия между
ними ( рис.3.11), то согласно третьему
закону динамики F F
1
откуда
F1 F2 0
2
.
Составив подобные равенства для всех
точек системы и просуммировав их,
i
получим
.
F К 0
6.
Аналогично, взяв произвольную точку О(рис.3.11) и составив уравнение моментов
относительно нее этих сил, получим
F1h F2 h 0
i
m o (F К ) 0
Рис. 3.11. Свойства внутренних сил
7.
3.3.2.Характеристикимеханической системы.
Масса системы равна сумме масс всех
ее точек
M m
K
Однако масса может распределяться по
всей системе неравномерно,
например, основная масса солнечной
системы сосредоточена на Солнце.
8.
Для характеристики распределениямассы по системе вводится понятие
центра масс.
Центр масс - это геометрическая точка,
координаты которой находятся по
формулам
XC
m
K
M
xK
,
YC
m
K
M
yK
, ZC
m
K
zK
M
где, mk - массы точек, входящих в систему,
Xk,Yk, Zk - координаты этих точек, M - масса
системы.
9.
Для однородного поля тяжести центр масссовпадает с центром тяжести.
Вместо трех формул (3.18), положение
центра масс можно определить с помощью
радиус-вектора центра масс
rC
mK rK
M
,
(3.19)
где rk - радиус-векторы отдельных точек.
10.
Пример. Найти положение центра тяжестисистемы, состоящей из двух точек,
массами m1=1кг и m2=2кг, находящихся на
расстоянии одного метра друг от друга
(рис.3.12).
Рис. 3.12. Рисунок к примеру
11.
Решение.Взяв начало координат в первой точке,
получим
m1 X 1 m2 X 2
XC
0
m1 m2
так как Х1=Х2=0.
Аналогично ZC=0.
m1Y1 m2Y2 0 2 1
YC
0,667 м.
m1 m2
1 2
То есть центр тяжести будет находиться на оси ОУ.
12.
• Следующая характеристикамеханической системы:
• Осевой момент инерции - величина,
равная сумме произведений масс
всех точек системы на квадрат
расстояния от этих точек до оси
J Z mK h
2
K
Данная величина является мерой
инертности твердого тела во
вращательном движении.
13.
Осевой момент инерции зависит отформы тела и расположения оси.
Для тонкого однородного кольца массой
М и радиусом R момент инерции
относительно оси, проходящей через
центр кольца, перпендикулярно его
плоскости (рис.3.13)
J Z mK h ( mK ) R MR
2
K
2
2
14.
• Аналогичные формулы можно получитьи для других тел простой формы
Например, момент инерции относительно
оси, проходящей через центр
однородного диска массы M и радиуса R,
перпендикулярно его плоскости
MR
JZ
2
2
15.
Для того, чтобы найти моменты инерциидля других осей, можно воспользоваться
теоремой Гюйгенса: момент инерции
относительно произвольной оси равен
сумме момента инерции относительно
оси, параллельной данной и
проходящей через центр масс, и
произведения массы тела на квадрат
расстояния между осями
J Z J ZC Md
2
16.
3.3.3. Теорема о движениицентра масс.
Рассмотрим механическую систему,
состоящую из n точек. Составим для
каждой точки системы выражение
второго закона динамики, подразделяя
силы на внешние и внутренние
e i
m1a1 F1 F1 ;
e i
m2 a2 F2 F2 ;
.......... .......... ....
e i
mn an Fn Fn .
(3.21)
17.
Данные уравнения называютсядифференциальными уравнениями
движения механической системы.
С помощью этих уравнений можно
полностью судить о движения всех точек
системы. Сложность решения уравнений в
том, что их может быть большое количество
и трудно определить внутренние силы,
поэтому они служат исходными
зависимостями, из которых можно получить
более простые формулы, позволяющие
судить о движении механической системы.
Одной из таких формул является теорема
о движении центра масс.
18.
• Для вывода теоремы просуммируемлевые и правые части уравнений
e
i
mK a K FK FK
• Согласно свойству внутренних сил
i
FK 0
• Из формулы (3.19) следует
MrC mK rK ,
(3.21)
19.
продифференцировав дважды по времени,получим
Ma m a ,
C
K
K
e
MaC Fk ,
Полученная формула и является теоремой
о движении центра масс: произведение
массы системы на ускорение центра
масс равно сумме внешних сил,
действующих на эту систему.
20.
• Если сумма всех внешних сил,действующих на систему, равна 0, то из
(3.22) следует, что ускорение центра масс
равно нулю, т.е. скорость центра масс
постоянна.
• Если сумма проекций внешних сил на
какую-либо ось х равна 0, то проекция
ускорения центра масс на эту ось будет
также равна 0, то есть проекция
скорости будет постоянна.
Данное положение называется законом
сохранения движения центра масс.
21.
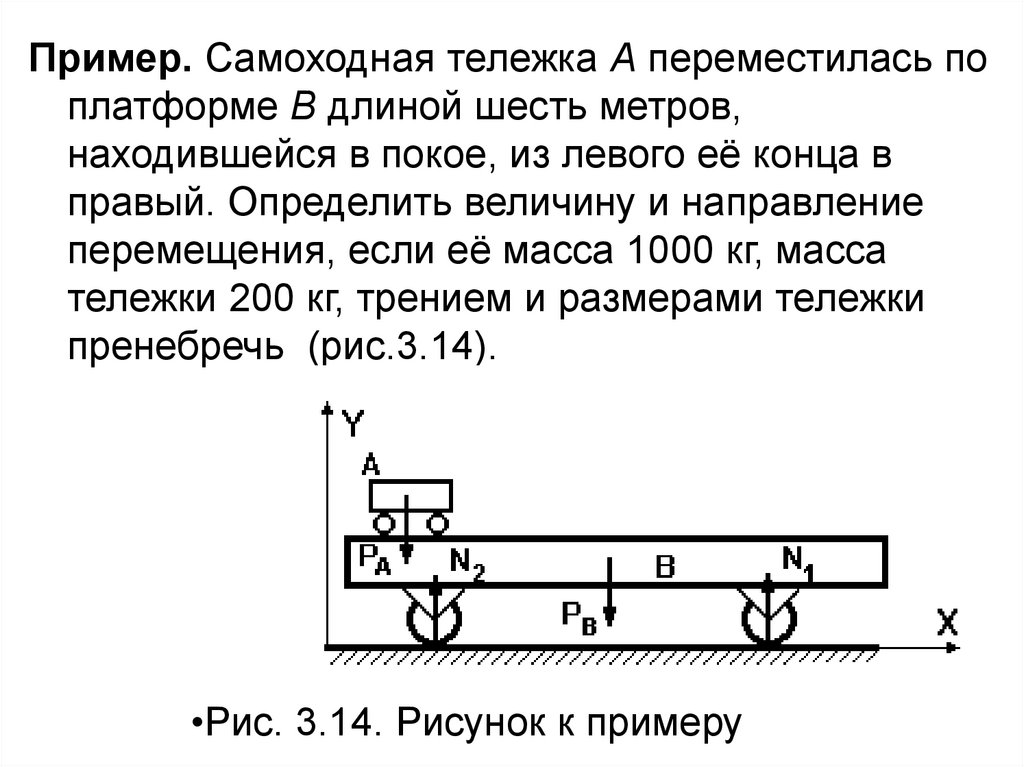
Пример. Самоходная тележка А переместилась поплатформе В длиной шесть метров,
находившейся в покое, из левого её конца в
правый. Определить величину и направление
перемещения, если её масса 1000 кг, масса
тележки 200 кг, трением и размерами тележки
пренебречь (рис.3.14).
•Рис. 3.14. Рисунок к примеру
22.
Решение. Используем теорему оe
движении центра масс ас Fk
Так как все внешние силы, действующие
на систему, перпендикулярны оси Х, то,
проектируя выражение на эту ось,
получим ас 0
или Vc const
• Поскольку в начальный момент система
находилась в покое, то Vc 0
или X c const
23.
то есть положение центра масс системыне изменится.
Система состоит из двух тел, поэтому
положение центра масс в начальный
момент определится из выражения
m1 X 1 m2 X 2
а)
со
где X1 и X2 - начальные координаты
тележки и платформы, а m1 и m2 – их
массы.
24.
При перемещении тележки под действиемвнутренних сил тележка и платформа
переместятся на ΔX1 и ΔX2 , тогда
координата центра масс будет равна
б)
m1 X 1 X 1 m2 X 2 X 2
с1
Приравнивая выражения а) и б), получим
m1 1 m2 2 0
25.
Перемещение платформы ΔX2 неизвестно, а перемещение тележкибудет равно
l
1
2
где l – длина платформы.
Отсюда получим
m1l
200 6
2
1м
m1 m2
200 1000
Знак (-) говорит о том, что платформа
переместится влево.
26.
3.3.4. Теорема об измененииглавного вектора количества
движения механической
системы.
Главным вектором количества
движения механической системы
называется векторная величина,
равная сумме количеств движения
всех точек системы
Q mkVk
27.
MrC mK rK ,Из формулы (3.19) следует, что
откуда MVC mKVK , следовательно
Q MVc
(3.23)
то есть главный вектор количества
движения равен произведению массы
системы на скорость центра масс.
Он будет равен нулю, если равна нулю
скорость центра масс, то есть
характеризует поступательное движение
системы со скоростью центра масс.
28.
Для вывода теоремы можно использоватьтеорему о движении центра
масс
e
MaC FK ,
e
так как a dVc , то dMVc
= Fk
C
dt
dt
или
t1
e
Md
V
=
F
k dt
C
V
0
c0
Vc1
После интегрирования получим
e
Q1 Q0 S K
29.
то есть изменение главного вектораколичества движения системы за
некоторый промежуток равно сумме
импульсов внешних сил,
воздействующих на эту систему.
Следствием этой теоремы является закон
сохранения главного вектора количества
движения механической системы.
30.
Если сумма импульсов внешних сил,действующих на систему, равна
нулю, то главный вектор количества
движения будет постоянным.
Если сумма проекций внешних сил на
ось х равна нулю, то постоянной
будет проекция главного вектора
количества движения системы на эту
ось.
31.
Примеры действия закона.1.Работа пропеллера или винта (рис.3.15).
Рис. 3.15. Работа пропеллера
32.
Принимая в качестве системы самолет иокружающий его воздух, видим, что, если
винт не вращается, количество движения
системы равно нулю, при включении
двигателя частицы воздуха
отбрасываются назад, при этом
количество движения системы не
изменится, поскольку движение винта
осуществляется под действием
внутренних сил. Следовательно, корпус
самолета будет двигаться вперед.
33.
Уравнение закона сохранения главноговектора количества движения примет
вид
mcVc mBVB 0
• где mc и mВ - массы самолета и
отбрасываемого воздуха, Vc и VВ -их
скорости. Отсюда скорость самолета
будет равна
mBVB
Vc
mc
34.
2. Реактивное движение.Отличие от предыдущего примера только в
том, что в этом случае отбрасываются не
частицы окружающей среды, а частицы
топлива.
3. Явление отката орудия или
отдача стрелкового ружья.
При движении одной из частей системы, а
именно снаряда или пули, которые движутся
под действием внутренних сил, из-за
сохранения главного вектора количества
движения лафет орудия или приклад ружья
движутся в противоположную сторону.
35.
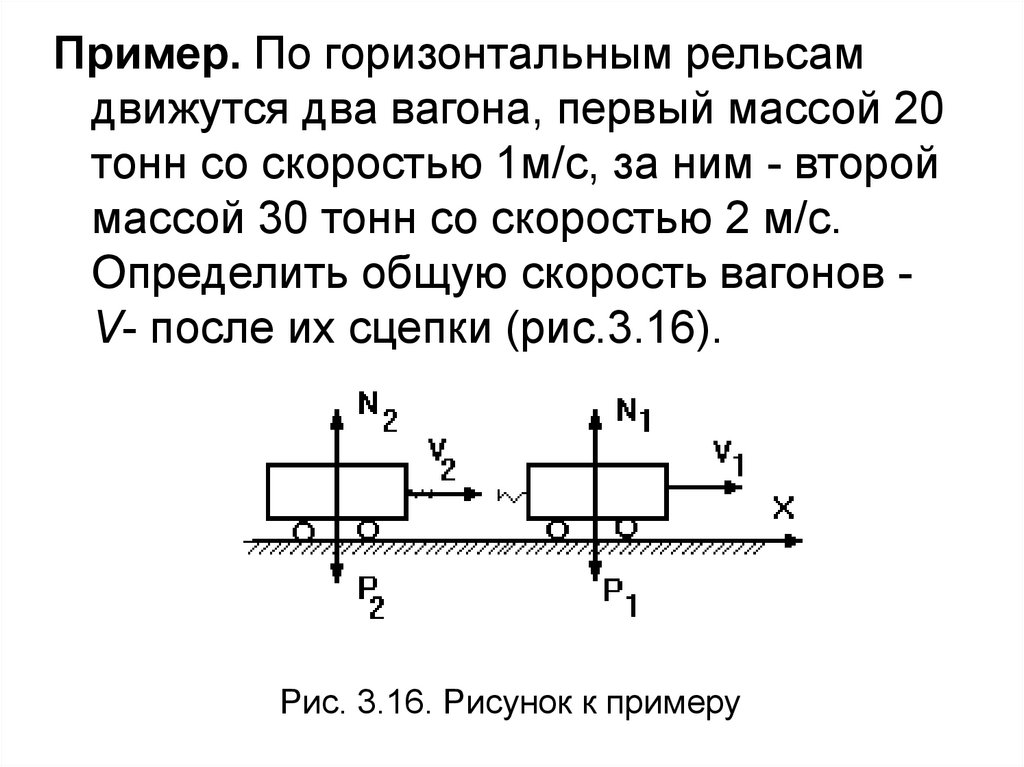
Пример. По горизонтальным рельсамдвижутся два вагона, первый массой 20
тонн со скоростью 1м/с, за ним - второй
массой 30 тонн со скоростью 2 м/с.
Определить общую скорость вагонов V- после их сцепки (рис.3.16).
Рис. 3.16. Рисунок к примеру
36.
Решение.Воспользуемся теоремой об изменении
главного вектора количества движения
системы
Q1 Q0 S
e
K
Проектируя это выражение на ось Х,
получим
Q1 X Q0 X 0 или Q1 X Q0 X .
Поскольку внешние силы
перпендикулярны оси Х, то проекции их
импульсов на эту ось равны нулю.
37.
Далее находим проекции главноговектора количества движения системы
на ось Х до и после сцепления вагонов
Q0 X m1V1 m2V2 ; Q1 X (m1 m2 )V .
Приравнивая эти величины, получим
m1V1 m2V2
V
1,6 м/с.
m1 m2
38.
3.3.5.Теорема об изменениикинетического момента
системы.
Главным моментом количества движения
системы относительно центра О (или
кинетическим моментом) называется
векторная величина, равная сумме
моментов количеств движений всех
точек системы относительно этого же
центра
K O mO (mkVk )
39.
Кинетическим моментом системыотносительно оси z называется
скалярная величина, равная сумме
моментов количеств движений всех
точек системы относительно этой
оси
K Z mZ (mkVk )
Кинетический момент характеризует
вращательное движение механической
системы.
40.
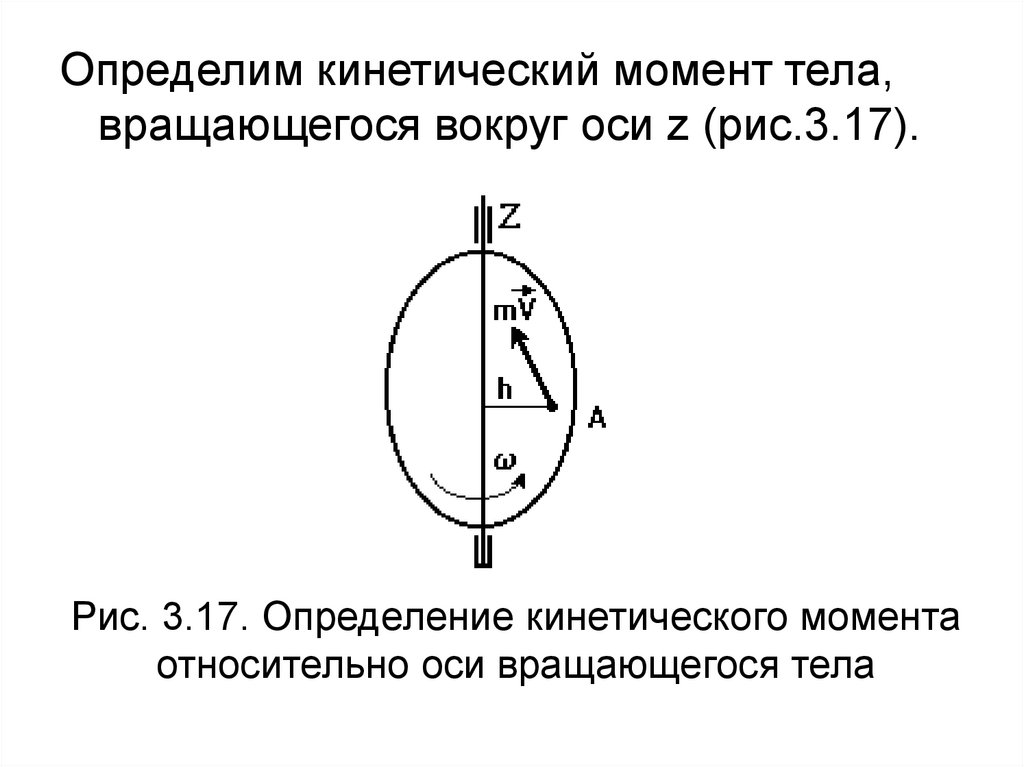
Определим кинетический момент тела,вращающегося вокруг оси z (рис.3.17).
Рис. 3.17. Определение кинетического момента
относительно оси вращающегося тела
41.
Для точки А, находящейся от оси Z на расстоянииh, момент количества движения относительно
этой оси равен
2
mZ ( mV ) mVh mh
Тогда для всего тела
K Z mZ (mk Vk ) (mk hk2 )
или
K Z J Z
(3.25)
то есть кинетический момент тела
относительно оси Z равен произведению
осевого момента инерции тела относительно
этой оси на угловую скорость
42.
Для доказательства теоремы составимвыражения теоремы об изменении
момента количества движения
относительно центра О для каждой
точки системы, подразделяя силы,
действующие на точки, на внешние и
внутренние, и просуммируем их левые
и правые части:
d
e
i
m o (m k V k ) m o ( Fk ) m o ( Fk )
dt
43.
Так кака
mo (mkVk ) K o ,
i
mo ( Fk ) 0
то получим
dK o
e
mo ( Fk )
dt
(3.26)
Данное выражение называется теоремой об
изменении кинетического момента
механической системы относительно
центра О: производная по времени от
кинетического момента системы
относительно центра О равна сумме
моментов внешних сил, действующих
на систему, относительно этого же
центра.
44.
Если это выражение спроектируем на осьz, то получим теорему об изменении
кинетического момента относительно
оси z
dK z
m z ( Fke )
dt
(3.27)
то есть производная по времени от
кинетического момента системы
относительно оси Z равна сумме
моментов внешних сил, действующих
на систему, относительно этой оси.
45.
Если сумма моментов внешних сил,действующих на систему,
относительно центра О или оси Z,
равна нулю, то из формул (3.26) и
(3.27) следует, что кинетические
моменты системы относительно
этого центра или оси будут
постоянными, то есть имеет место
закон сохранения кинетического
момента
KO const , K Z const
46.
Примером действия этого закона являетсяскамейка Жуковского (рис. 3.18). Если человеку,
стоящему на ней с разведенными в стороны
руками, сообщить небольшую угловую скорость,
а затем опустить руки,
то скорость вращения
увеличится, поскольку
сумма моментов внешних
сил относительно оси Z
равна нулю.
Рис. 3.18. Скамейка Жуковского
47.
Кинетический момент, а осевой моментинерции JZ при опускании рук уменьшится.
Данной теоремой пользуются, как правило,
для изучения вращательного движения
твердых тел или механизмов, в которые
они входят.
Пример.
К маховику, представляющему собой
однородный диск массой m и радиусом r,
приложен вращающий момент М (рис.3.19).
48.
Определить угловоеускорение маховика.
Рис. 3.19. Маховик
Решение.
Применим теорему об изменении
кинетического момента относительно оси z,
проходящей через центр диска.
2
Кинетический момент
mr
K Z J Z
2
49.
Сумма моментов внешних сил относительноe
оси Z
m (F ) M
z
k
(моменты сил N и Р равны нулю, так как эти
силы пересекают ось Z). Подставляя в
(3.27), имеем
dK z mr 2 d mr 2
M.
dt
2 dt
2
Отсюда
2M
2
mr
50.
3.3.6.Теорема об изменениикинетической энергии
системы.
Кинетической энергией системы
называется скалярная величина,
равная сумме кинетических энергий
всех точек системы
mkVk2
T
.
2
(3.28)
51.
Кинетическая энергия характеризует каквращательное, так и поступательное
движение системы и является
скалярной положительной величиной.
Формулы для вычисления кинетической
энергии твердых тел зависят от вида
движения.
52.
Поступательное движение.В этом случае скорости всех точек тела равны
скорости центра масс, поэтому формула
(3.28) примет вид
2
k
mkV
1
T
( mk )VC2
2
2
или
MVC2
T
.
2
(3.29)
То есть в этом случае кинетическая энергия
равна половине произведения массы тела
на квадрат скорости центра масс.
53.
Вращательное движение.Скорость любой точки вращающегося тела равна
произведению угловой скорости на расстояние от
этой точки до оси вращения. Подставляя в
формулу (3.28), имеем
mV2 1
Поскольку
m h
k
окончательно
2
k
JZ
T
J Z 2
T
2
k
2
k
( mk hk2 ) 2
2
(3.30)
то есть кинетическая энергия равна половине
произведения осевого момента инерции
относительно оси вращения на квадрат угловой
скорости.
Сравнивая формулы (3.29) и (3.30), можно подтвердить
вывод о том, что осевой момент инерции является
мерой инертности тела во вращательном
движении.
54.
Плоскопараллельное движениеЭто движение можно представить в виде совокупности
поступательного движения со скоростью центра
масс и вращательного вокруг оси, проходящей
через центр масс перпендикулярно плоскости
движения. Поэтому выражение для кинетической
энергии примет вид
MVC2 J ZC 2
T
2
2
(3.31)
Следовательно, при плоскопараллельном движении
кинетическая энергия тела равна сумме энергии
поступательного движения со скоростью
центра масс и энергии вращательного
движения вокруг центра масс.
55.
Для доказательства теоремы составимвыражения теоремы об изменении
кинетической энергии для каждой точки
системы, подразделяя силы, действующие
на точки, на внешние и внутренние, и
просуммируем их левые и правые части:
mk Vk2
d (
) dAke dAke
2
dT dA dA .
e
k
i
k
Данное равенство выражает теорему об
изменении кинетической энергии системы в
дифференциальной форме.
56.
Проинтегрировав обе части этого выражения впределах, соответствующих перемещению
системы из некоторого начального положения
в конечное, получим данную теорему в
конечном виде
T1 T0 A A ,
e
k
i
k
(3.33)
то есть изменение кинетической энергии
системы при ее некотором перемещении
равно сумме работ внешних и внутренних
сил
57.
В общем случае, как следует из этоговыражения, внутренние силы могут влиять на
кинетическую энергию системы.
Если же расстояния между точками
приложения внутренних сил не изменяются
(такая система называется неизменяемой, к
ней относятся, например, абсолютно твердое
тело или нерастяжимая нить), то для такой
системы работа внутренних сил равна нулю,
и выражение для теоремы об изменении
кинетической энергии примет вид
T1 T0 A .
e
k
58.
Данная теорема используется прирешении задач, в которых в число
искомых или заданных величин входят
перемещения точек системы, их
скорости и силы.
59.
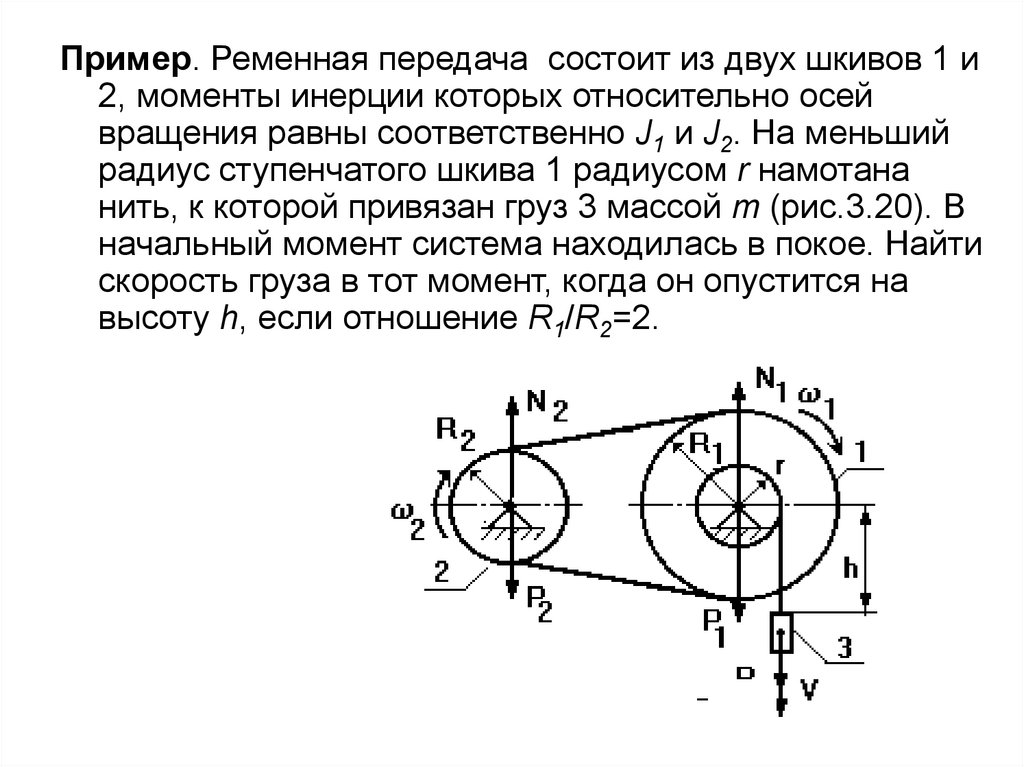
Пример. Ременная передача состоит из двух шкивов 1 и2, моменты инерции которых относительно осей
вращения равны соответственно J1 и J2. На меньший
радиус ступенчатого шкива 1 радиусом r намотана
нить, к которой привязан груз 3 массой m (рис.3.20). В
начальный момент система находилась в покое. Найти
скорость груза в тот момент, когда он опустится на
высоту h, если отношение R1/R2=2.
60.
Решение. Используем теорему обизменении кинетической энергии
механической системы
T1 T0 A .
e
k
Кинетическая энергия в начальный
момент времени Т0=0, поскольку все
тела находились в покое.
Кинетическая энергия в конечный момент
времени
Т1=Т(1)+Т(2)+Т(3)
61.
где-
T(1)
J 1
,
2
2
1
T( 2)
J 2
2
2
2
кинетическая энергия шкивов,
T(3)
mV 2
.
2
- кинетическая энергия груза.
Угловые скорости выражаем через скорость
груза
1
V
r
, 2
1 R1
R2
2V
r
62.
Подставляя в выражение кинетическойэнергии, имеем
2
V
2
T1 2 (mr J 1 4 J 2 )
2r
Находим работу внешних сил. Работу
будет совершать только сила тяжести
груза - Р3 , поскольку остальные
внешние силы – Р1, Р2, N1, N2
приложены в неподвижных точках
A P3h mgh.
e
k
63.
После подстановки в выражение теоремыоб изменении кинетической энергии
получим
2
2mghr
V
2
mr J1 4 J 2
64.
Пример. Определить, какую угловую скоростьбудет иметь кривошип ОА кривошипноползунного механизма (рис.3.21), после того
как к нему был приложен постоянный
вращающий момент М и он совершит один
оборот из данного положения.
В начальный момент система находилась в
покое. Кривошип ОА считать однородным
стержнем длиной L и массой m1, шатун АВ
имеет массу m2,массой ползуна В
пренебречь.
65.
Решение. Используем теорему обизменении кинетической энергии
механической системы
1 0 А к
Кинетическая энергия системы в
начальный момент равна нулю Т0=0.
Кинетическая энергия в конечный момент
(после того как кривошип сделал один
оборот и вернулся в прежнее
положение)
1 1 2
66.
Где1
2
J t 1
2
- кинетическая энергия кривошипа,
2
2
m 2 Vc
2
- кинетическая энергия шатуна.
Нужно отметить, что в данном положении
угловая скорость шатуна равна нулю и
скорости всех его точек одинаковы, то
есть
Vc VA 1 L
67.
Осевой момент инерции кривошипа2
m1 L
J1
3
Подставляя эти значения в выражении
кинетической энергии, получим
m1L2 2 m 2 L2 2 L2 12
m1 3m 2
1
1
1
3 2
2
6
• Определим работу
А
к
Ам А 1 А 2
а)
68.
Работа вращающего моментам 2
б)
Работа сил тяжести за один оборот
кривошипа равна нулю, поскольку
центры тяжести тел возвращаются в
прежнее положение, .
1 2 0
Приравнивая выражения а) и б), получим
2 2
L 1
1
4
m1 3m2 2
1
2
L m1 3m2
69.
3.3. Принцип Даламбера
3.3.1. Принцип Даламбера для материальной точки и системы. Методы
решения задач механики, которые до сих пор рассматривались,
основываются на уравнениях, вытекающих или непосредственно из
законов Ньютона, или же из общих теорем, являющихся следствием
этих законов.
Однако этот путь не является единственным. Оказывается, что
уравнения движения или условия равновесия механической системы
можно получить, положив в основу вместо законов Ньютона другие
общие положения, называемые принципами механики. В ряде случаев
применение этих принципов позволяет, как мы увидим, найти более
эффективные методы решения соответствующих задач. В этой главе
будет рассмотрен один из общих принципов механики, называемый
принципом Даламбера.
Найдем сначала выражение принципа для одной материальной точки.
Пусть на материальную точку с массой m действует система активных
сил, равнодействующую которых обозначим Р, и реакция связи N (если
точка является несвободной). Под действием всех этих сил точка будет
двигаться по отношению к инерциальной системе отсчета с некоторым
ускорением а.
Введем в рассмотрение величину F и, ma имеющую размерность силы.
Векторную величину, равную по модулю произведению массы точки на
ее ускорение и направленную противоположно этому ускорению,
называют силой инерции точки.
70.
• Тогда оказывается, что движение точки обладает следующимсвойством: если в любой момент времени к действующим на
точку активным силам и реакции связи присоединить силу
инерции, то полученная система сил будет уравновешенной.
a и
F N F 0. (3.35)
• Это положение выражает принцип Даламбера для
материальной точки. Нетрудно убедиться, что оно эквивалентно
второму закону Ньютона и наоборот
• Рассмотрим теперь механическую систему, состоящую из n
материальных точек.
• Выделим какую-нибудь из точек системы с массой .
• Под действием приложенных к ней внешних и внутренних сил и
(в которые входят и активные силы, и реакции связей) точка
будет двигаться по отношению к инерциальной системе отсчета
с некоторым ускорением . Введя для этой точки силу инерции ,
получим F e F i F и 0,
k
k
k
71.
то есть на точку действует уравновешенная система сил.
Повторяя такие рассуждения для каждой из точек системы, придем к
следующему результату, выражающему принцип Даламбера для
системы: если в любой момент времени к каждой из точек системы,
кроме действующих на нее внешних и внутренних сил, присоединить
соответствующие силы инерции, то полученная система сил будет
уравновешенной и к ней можно применять все уравнения статики.
Математически принцип Даламбера для системы выражается
векторными равенствами вида, которые, очевидно, эквивалентны
дифференциальным уравнениям движения системы. Следовательно,
из принципа Даламбера можно получить все общие теоремы динамики.
Значение принципа Даламбера состоит в том, что при
непосредственном его применении к задачам динамики уравнения
движения системы составляются в форме хорошо известных
уравнений равновесия; это делает единообразным подход к решению
задач и часто упрощает соответствующие расчеты. Кроме того, в
соединении с принципом возможных перемещений, который будет
рассмотрен в следующей главе, принцип Даламбера позволяет
получить новый общий метод решения задач динамики.
Из статики известно, что геометрическая сумма сил, находящихся в
равновесии, и сумма их моментов относительно любого центра О
равны нулю, причем это справедливо для сил, действующих не только
на твердое тело, но и на любую изменяемую механическую систему.
72.
• Тогда на основаниипринципа
Даламбера
[
M
(
F
)
M
(
F
)
M
( F ) 0.
должно быть (F F F ) 0,
R
F
,
M
M
(
F
) 0.
• Введем обозначения
• Величины и представляют собою главный
вектор и главный момент относительно
центра О системы сил инерции. В результате,
учитывая, что геометрическая сумма
внутренних сил и сумма их моментов равны
нулю, получим
• .
(3.36) F R 0, M (F ) M 0
• Применение этих, вытекающих из принципа
Даламбера, уравнений, упрощает процесс
решения задач, так как эти уравнения не
содержат внутренних сил.
e
k
и
k
i
k
и
е
k
e
k
o
и
k
и
о
и
o
е
k
i
k
o
o
и
о
o
и
k
и
k
73.
• Чтобы пользоваться ими при решении задач,надо знать выражения главного вектора и
главного момента сил инерции.
• В заключение следует подчеркнуть, что при
изучении движения по отношению к
инерциальной системе отсчета, которое
здесь и рассматривается, силы инерции
вводятся только тогда, когда для решения
задач применяется принцип Даламбера.
• 3.3.2.Главный вектор и главный момент сил
инерции. Из уравнения
(3.35) следует, что
R F ,
M M ( F )
• .
• Сравнивая первое из равенств с уравнением
теоремы о движении центра масс, получим
и
Мас Fkе ,
е
k
и
R Мас
и
о
o
е
k
74.
• то есть главный вектор сил инерции механической системы (вчастности, твердого тела) равен произведению массы системы
(тела) на ускорение центра масс и направлен противоположно
этому ускорению.
• Сравнив теперь второе из равенств (3.35) с уравнением
dK o
• ,
M o ( Fke )
dt
• выражающим теорему об изменении кинетического момента, и
учтя, что аналогичным будет соотношение для моментов
относительно оси, получим и
dK o
dK z
и
M
,
m
о
z
• ,
(3.38)
dt
dt
• то есть главный момент сил инерции механической системы
(твердого тела) относительно некоторого центра О или оси z
равен взятой со знаком минус производной по времена от
кинетического момента системы (тела) относительно того же
центра или той же оси.
75. 3.3.3.Приведение сил инерции твердого тела.
• Систему сил инерции твердого тела можнозаменить одной силой, равной и приложенной в
произвольно выбранном центре О, и парой с
моментом, равным . Рассмотрим несколько
частных случаев.
• 1. Поступательное движение. В этом случае
ускорения всех точек тела одинаковы и равны
ускорению центра масс тела . Тогда все силы
инерции образуют систему параллельных сил,
аналогичных силам тяжести, и поэтому, как и
силы тяжести, имеют равнодействующую, проходящую через точку С.
76.
Следовательно, при поступательном движениисилы инерции твердого тела приводятся к
равнодействующей, равной и проходящей через
центр масс тела.
2. Вращение вокруг оси, проходящей через центр
масс тела. Если тело вращается вокруг оси Cz,
проходящей через центр масс С тела, то , так как
. Следовательно, в этом случае система сил
инерции тела приводится к одной только паре с
моментом , лежащей в плоскости симметрии
тела.
Так как кинетический момент относительно оси
вращающегося тела равен
K z J z
то есть
dK z
J z d
m
J z
dt
dt
и
z
77.
• Следовательно, величина момента будет равна произведениюосевого момента инерции на угловое ускорение тела, а
направлен он будет противоположно угловому ускорению.
• 3. Плоскопараллельное движение. Если тело имеет плоскость
симметрии и движется параллельно этой плоскости, то,
очевидно, система сил инерции тела приведется к лежащим в
плоскости симметрии силе, равной и приложенной в центре
масс тела, и паре сил моментом .
• Пример. На однородный диск массой m1 намотана нить, к
которой привязан груз массой m2. Определить ускорение груза,
реакцию опоры и силу натяжения нити (рис.3.22).
• Решение. Применим принцип Даламбера для системы,
состоящей из груза и диска. Прикладываем внешние силы Р1,
Р2, No, к грузу – силу инерции .
78.
• Силы инерции в диске приводятся к паре смоментом
m2 r 2 a
и
mz J z
• .
2 r
• Составляем уравнения равновесия:
mz ( Fk ) 0;
m èz F è r P1r 0 ,
(a)
Fky 0;
N o Fè P1 P2 0 .
( á)
• Подставляя значения в уравнение (а),
получим
m2 r 2 a
2m1
2
r
m1ar m1 gr 0,
a
• Из уравнения (б) находим
2
2
m
1
N o P1 P2 F и (m1 m2 ) g
g
m2 2m1
m 2 2m1
g.
79.
• Для нахождения силы натяжения нитиприменим принцип Даламбера отдельно
для груза (рис.3.22,б). Составляем
уравнение равновесия груза
2
2
m
1
T F и P1 0; T P1 F и m1 g
g
m2 2m1
80.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ1. Сформулируйте основные законы механики.
2. Какова мера инертности твердых тел при поступательном
движении?
3. Какую систему отсчета называют инерциальной?
4. Каковы две основные задачи динамики точки, которые решаются
при помощи дифференциальных уравнений движения
материальной точки?
5. Как определяются постоянные при интегрировании
дифференциальных уравнений движения материальной точки?
6. Как классифицируют в динамике силы, действующие на точки
механической системы?
7. Что называют центром масс системы точек и как определяют
его координаты?
8. Сформулируйте теорему о движении центра масс системы.
9. При каких условиях центр масс системы находится в состоянии
покоя?
10. Как определяются моменты количества движения
материальной точки относительно центра и относительно оси?
Какова зависимость между ними?
11. При каком расположении вектора количества движения
материальной точки его момент относительно оси равен нулю?
81.
12. Сформулируйте теорему об изменении момента количествадвижения материальной точки относительно центра и относительно
оси.
13. Что называется осевым моментом инерции твердого тела?
14. Какая зависимость между осевыми моментами инерции тела
относительно параллельных осей?
15. Что называют кинетическим моментом механической системы
относительно центра или оси?
16. Сформулируйте теорему об изменении кинетического момента
механической системы относительно центра и относительно оси.
17. Как определяется работа постоянной по модулю и направлению
силы на прямолинейном перемещении?
18. Как вычисляется работа силы тяжести и работа силы упругости?
19. Сформулируйте теорему об изменении кинетической энергии
материальной точки.
20. Как вычисляется кинетическая энергия твердого тела в различных
случаях его движения?
21. Сформулируйте теорему об изменении кинетической энергии
механической системы.
22. В чем заключается сущность принципа Даламбера для
материальной точки?
23. Каковы модуль и направление главного вектора сил инерции
механической системы?
82.
ЛИТЕРАТУРА1. Тарг С.М. Краткий курс теоретической механики. –
М.: Высшая школа, 1986. – 415 с.
2. Мещерский Н.В. Сборник задач по теоретической
механике. – М.: Наука, 1986. –447 с.
3. Яблонский А.А. и др. Сборник задач для курсовых
работ по теоретической механике. – М.: Высшая
школа, 1985. –366 с.
4. Воронков И.М. Курс теоретической механики.– М.:
Наука, 1986.–596 с.
5. Бутенин Н.В. Краткий курс теоретической механики.
– М.: Наука, 1985. –486 с.
6. Митягин Н.П., Пирогов С.П. Понятия, формулы,
уравнения теоретической механики (справочник). –
Тюмень: Вектор Бук, 2002.- 100 с.














































































 Физика
Физика








