Похожие презентации:
Модуль и его приложения. Понятие модуля
1.
Модуль и егоприложения
L/O/G/O
www.themegallery.com
2. Понятие модуля
Абсолютной величиной (модулем)действительного числа а называется само
число а, если оно неотрицательное, и число,
противоположное а, если а – отрицательное.
a , если а 0;
a
а , если а 0.
2x 3, если x 1,5;
Пример: 2x 3
2x 3, если x 1,5.
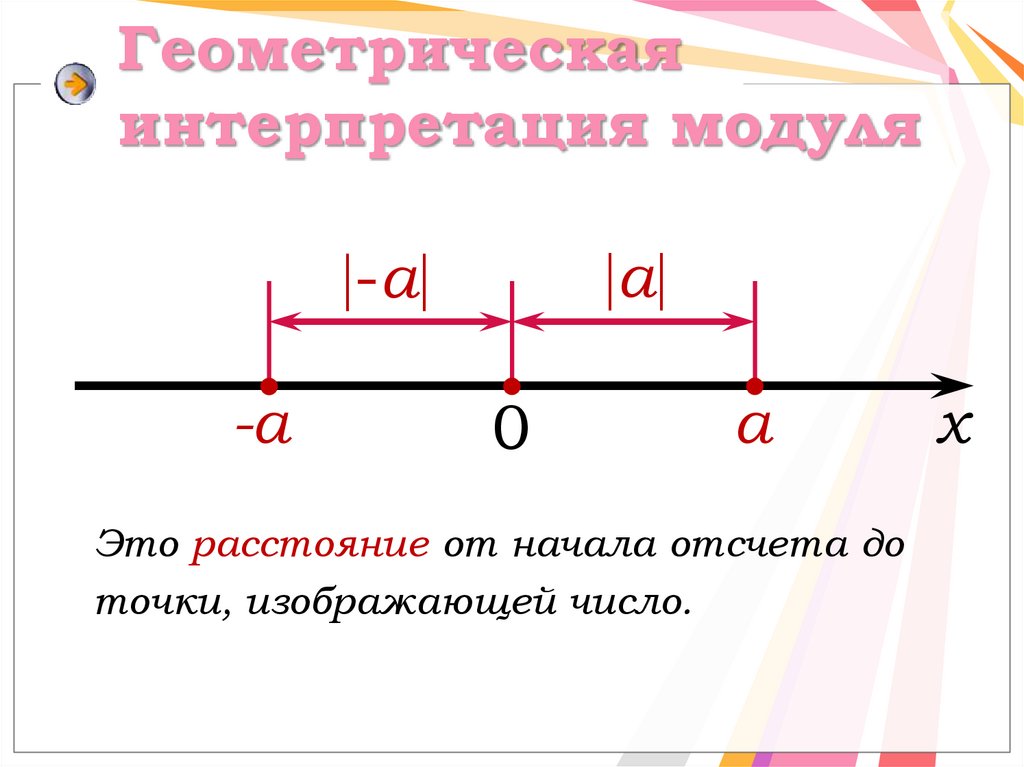
3. Геометрическая интерпретация модуля
а-а
-а
0
а
Это расстояние от начала отсчета до
точки, изображающей число.
х
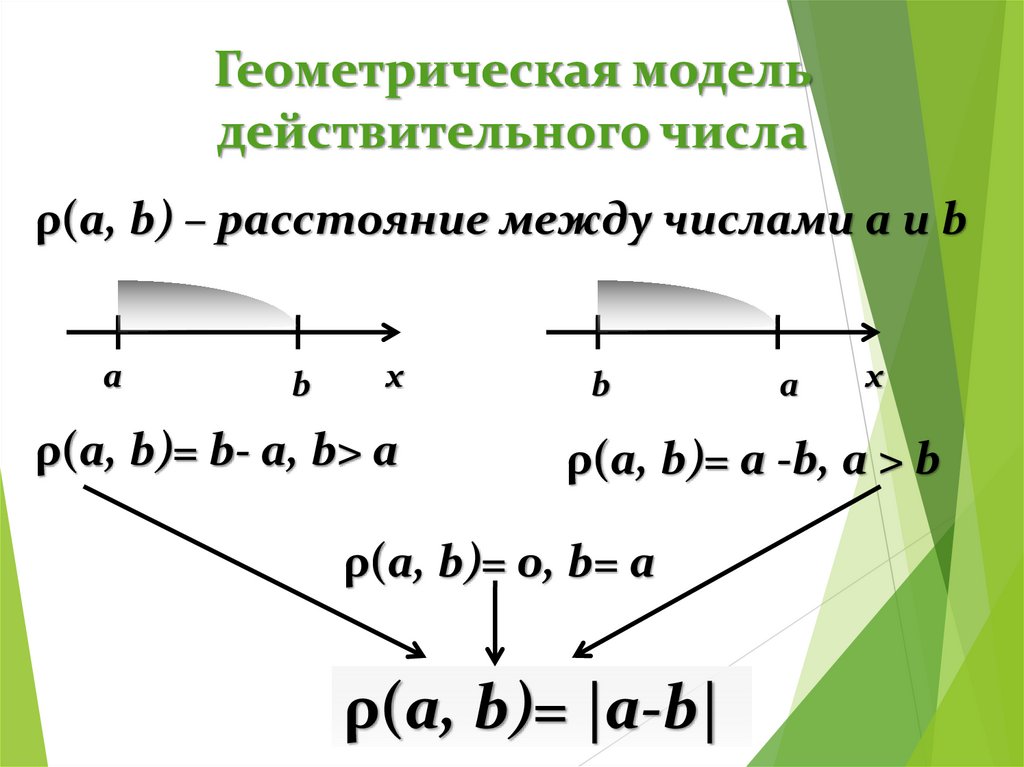
4. Геометрическая модель действительного числа
ρ(a, b) – расстояние между числами a и ba
b
х
ρ(a, b)= b- a, b> a
b
a
х
ρ(a, b)= a -b, a > b
ρ(a, b)= 0, b= a
ρ(a, b)= |a-b|
5. Примеры Раскрыть модули:
1) p 3 ;2)
3 5;
3)
5 2;
4) 1 2 ;
5) x 2 ;
6) x 1 ;
4
7) ( a 3 ) , a 3 ;
2
8) ( b 4 ) , b 4 ;
2
9) m 2m 1,
2
m 1.
6. Решение уравнений вида f(x)= a
Решение уравнений видаf(x) = a
f (x ) a ,
f (x ) a.
Пример: x – 8 =5
x 8 5,
x 13,
x 8 5; ⇔
x 3.
Ответ: 3; 13.
7. Решение уравнений вида |f(x)|= a
|2x – 3|= 4|5x + 6|= 7
|9 – 3x |= 6
|4x + 2|= – 1
|8 – 2x|= 0
|10x + 3|= 16
|24 – 3x|= 12
|2x + 30|= 48
x1 = 3,5; x2 = – 0,5
x1 = 0,2; x2 = – 2,6
x1 = 1;
x2 = 5
x Ø
x=4
x1 = 1,3; x2 = – 1,9
x1 = 12; x2 = 4
x1 = 9;
x2 = – 39
8.
Решите уравнениех<-7
-7≤x≤0 x>0
9.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
g
(
x
)
0
;
f (x ) g (x ),
g (x ) 0.
или
f (x ) g (x ),
f (x ) g (x ),
g (x ) 0;
10. Пример: 3х –10 = х – 2
Пример: 3х –10 = х – 23x 10 x 2,
2x 8,
x
2
0
;
x
2
;
3x 10 (x 2), ⇔ 4x 12, ⇔
x 2 0;
x 2;
x 4,
⇔ x 3.
Ответ: 3; 4.
11.
Решение уравнений |f(x)|=|g(x)|.1способ
|f(x)|=|g(x)| <=> f2(x) = g2(x) <=>
<=>(f(x) + g(x)) (f(x) - g(x))=0 <=> f(x) g(x) 0;
f(x) g(x) 0.
2 способ
|f(x)|=|g(x)| <=> f ( x) g ( x),
f ( x) g ( x).
12.
Решение уравнений видаf(x) = g(x)
f (x ) g (x ),
f (x ) g (x ).
Пример: x – 2 = 3 – x
x 2,5,
x 2 3 x ,
2x 5,
x 2 3 x ; ⇔ 2 3; ⇔ x Ø ;
Ответ: 2,5.
13. Решить самостоятельно: 4x –1 = 2х + 3
Решить самостоятельно:4x –1 = 2х+ 3
x 2,
4x 1 2x 3,
2x 4,
4x 1 2x 3; ⇔ 6х 2; ⇔ x 1 .
3
1
Ответ: 2; – ---.
3
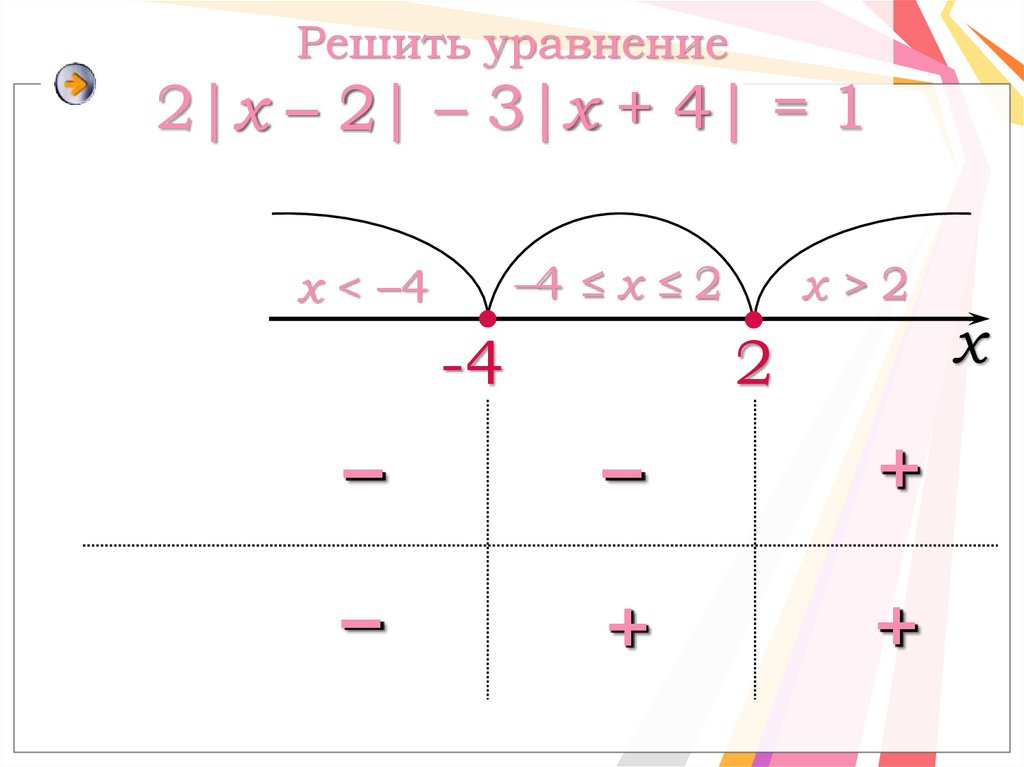
14. Решить уравнение 2|x – 2| – 3|х + 4| = 1
Решить уравнениеx+4
2|x
2| – 3|х
4| = 1
x–2
–4 ≤ x ≤ 2
x < –4
-4
x>2
2
–
–
+
–
+
+
х
15. Решить уравнение 2x – 2 – 3х + 4 = 1
Решить уравнение2 x – 2 – 3 х + 4 = 1
x 4,
2( x 2) 3( x 4) 1;
4 x 2,
2( x 2) 3(x 4) 1;
x 2,
2(x 2) 3(x 4) 1;
⇔
x 4,
x 15;
4 x 2,
x 1,8;
x 2,
x 17.
Ответ: –15; –1,8.
16. Примеры (решить самостоятельно)
1) x2 + 3x = 2(x + 1)2) x – 6 = x2 – 5x + 9
3) 2x + 8 – x – 5 = 12
1) Ответ: 1; (–5 + √17)/2.
2) Ответ: 1; 3.
3) Ответ: -25; 3.
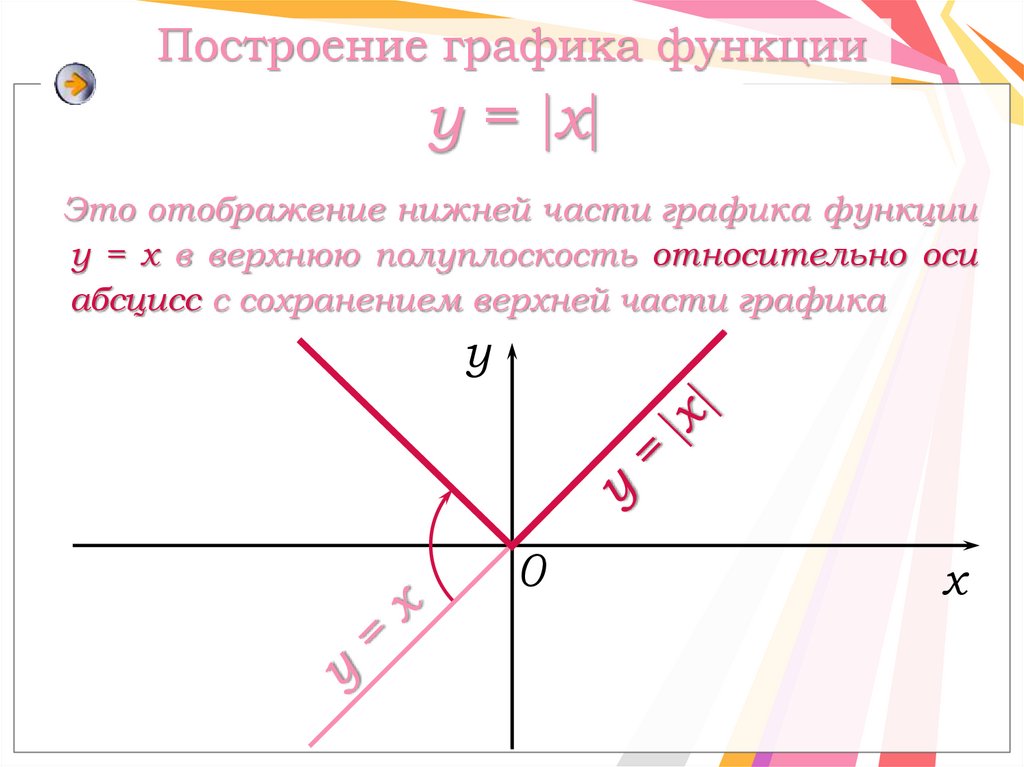
17. Построение графика функции y = x
Построение графика функцииy = x
Это отображение нижней части графика функции
y = x в верхнюю полуплоскость относительно оси
абсцисс с сохранением верхней части графика
y
0
x
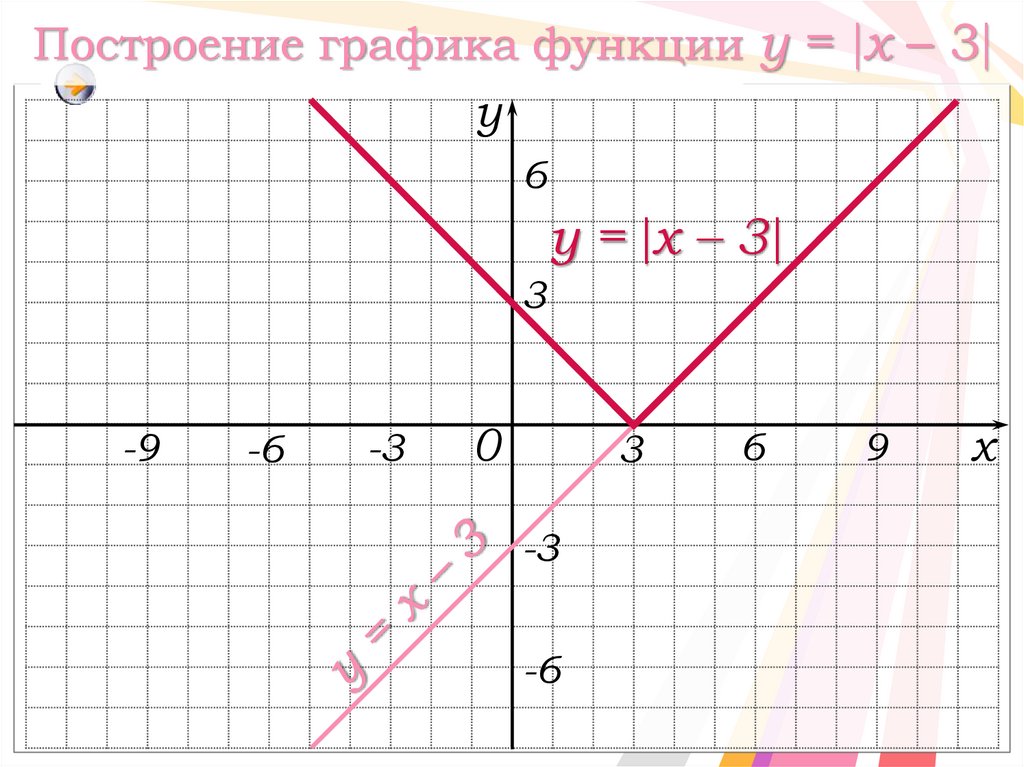
18. Построение графика функции y = x – 3
Построение графика функции y = x – 3y
6
y = x – 3
3
-9
-6
-3
0
3
-3
-6
6
9
x
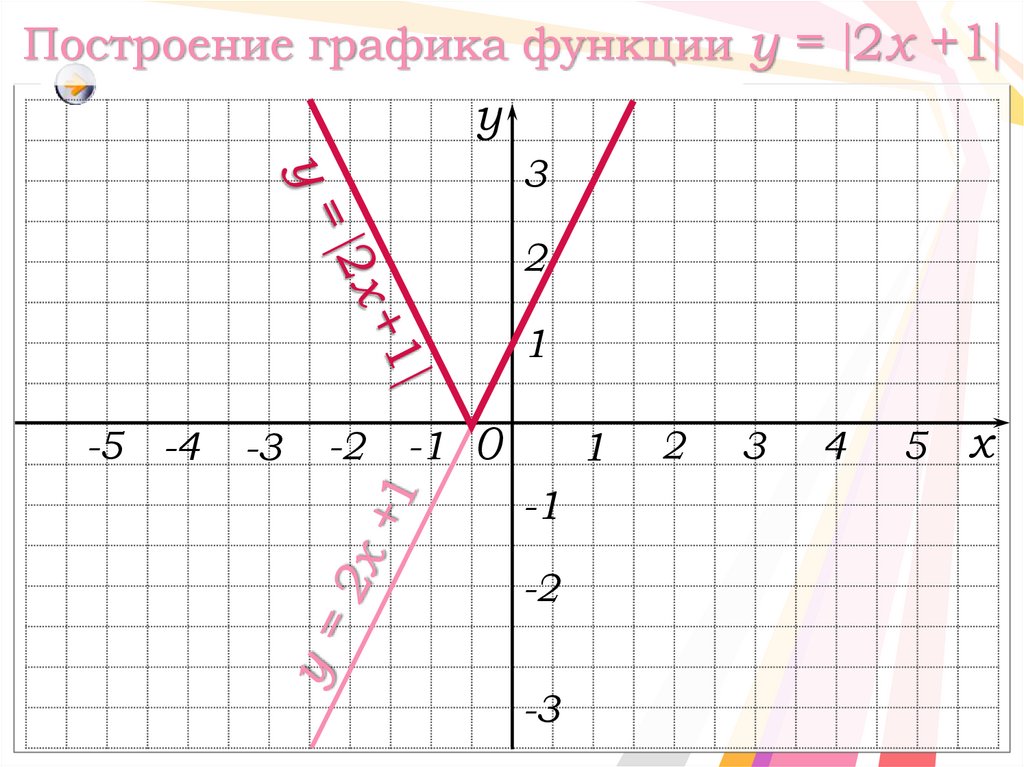
19. Построение графика функции y = 2x +1
Построение графика функции y = 2x +1y
3
2
1
-5 -4
-3
-2
-1 0
1
-1
-2
-3
2
3
4
5
x
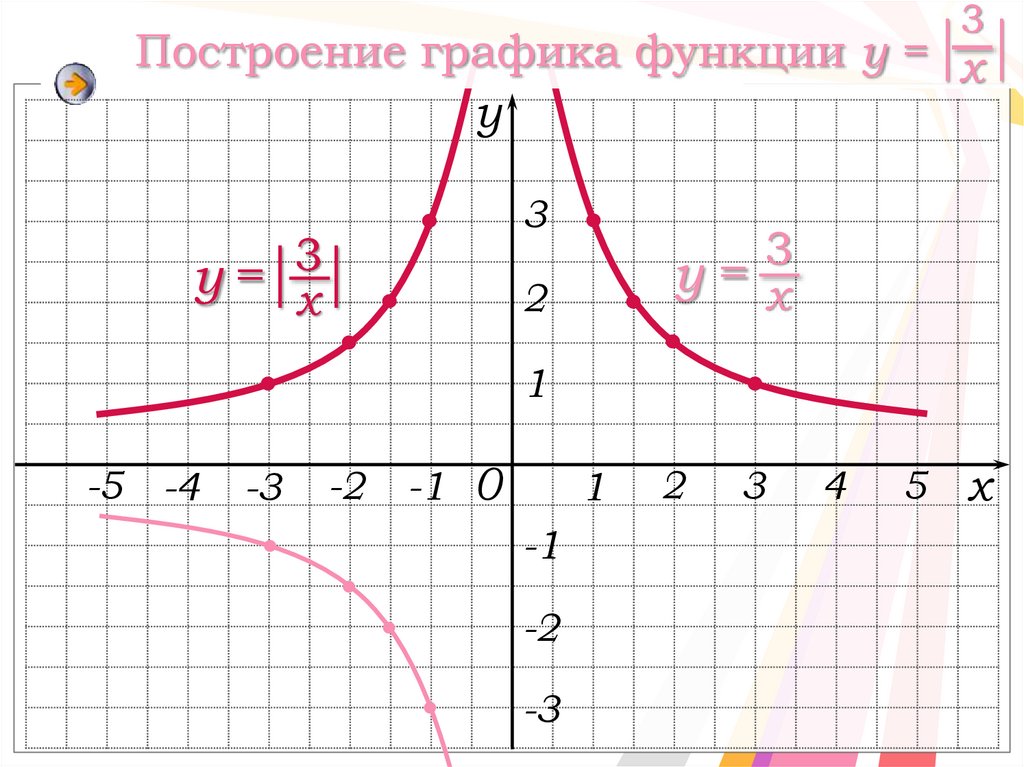
20.
3Построение графика функции y = х
y
3
3
y= х
3
y= х
2
1
-5 -4
-3
-2
-1 0
1
-1
-2
-3
2
3
4
5 x
21.
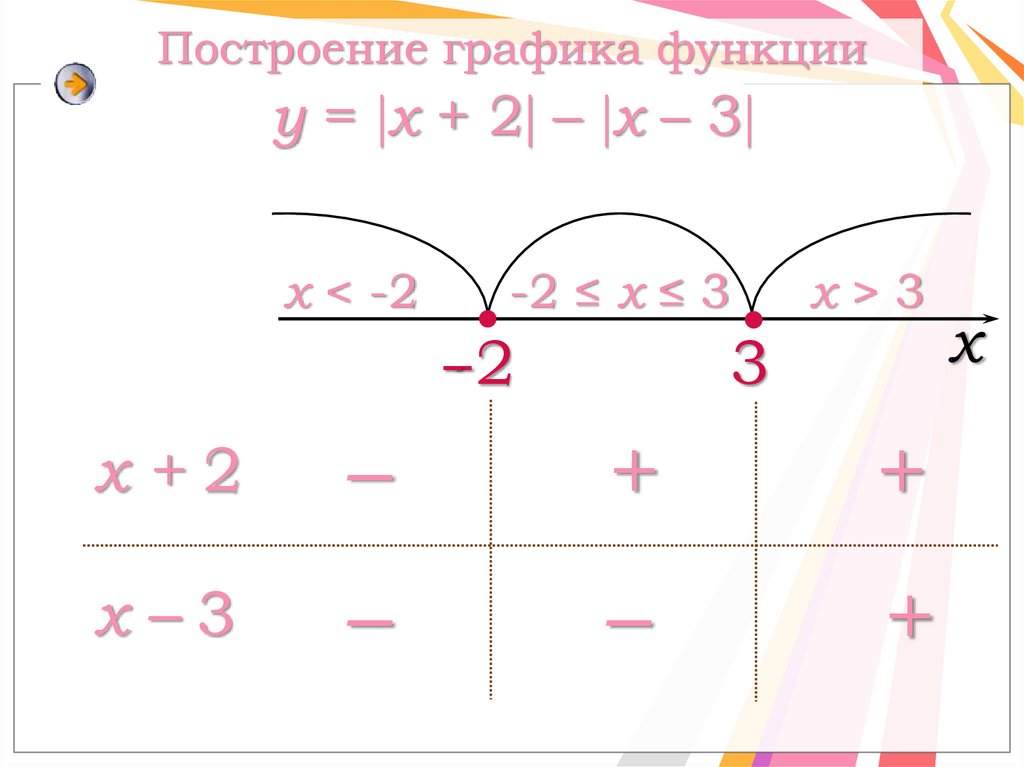
Построение графика функцииy = x + 2 – x – 3
x < -2
-2 ≤ x ≤ 3
--2
x>3
3
x+2
–
+
+
x–3
–
–
+
x
22.
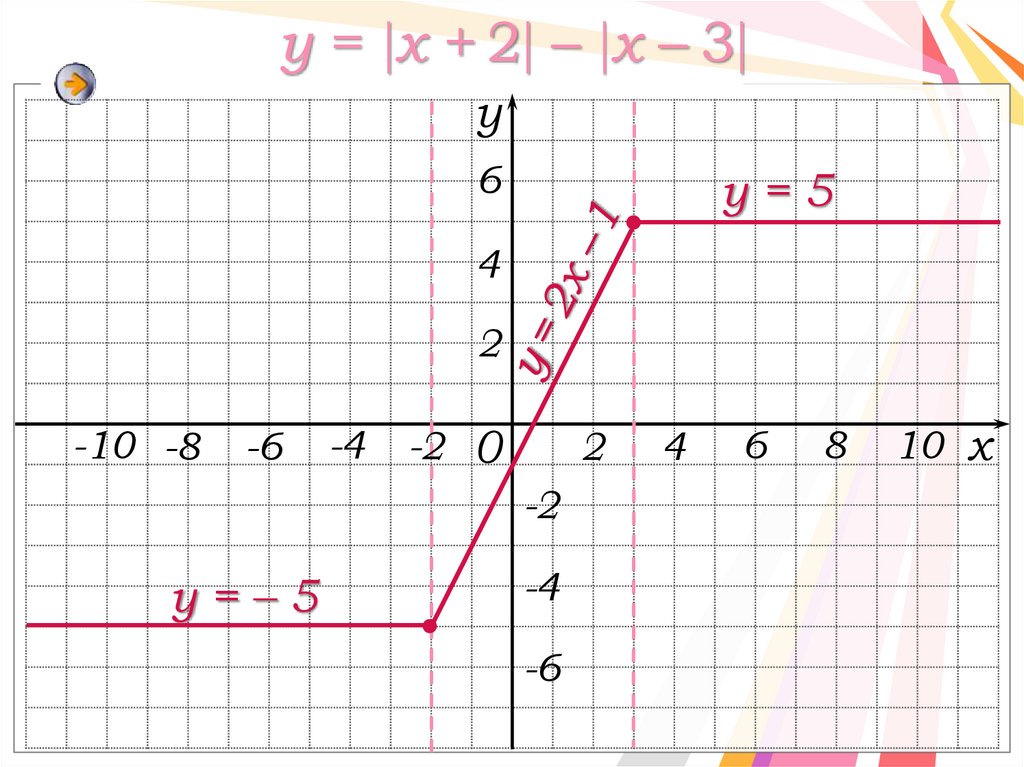
Построение графика функцииy = x + 2 – x – 3
x 2,
y x 2 x 3;
2 x 3,
y x 2 x 3;
x 3,
y x 2 x 3;
⇔
x 2,
y 5;
2 x 3,
y 2x 1;
x 3,
y 5.
23.
y = x + 2 – x – 3y
6
у=5
4
2
-10 -8
-6
-4
-2 0
2
-2
у=–5
-4
-6
4
6
8
10 x
24.
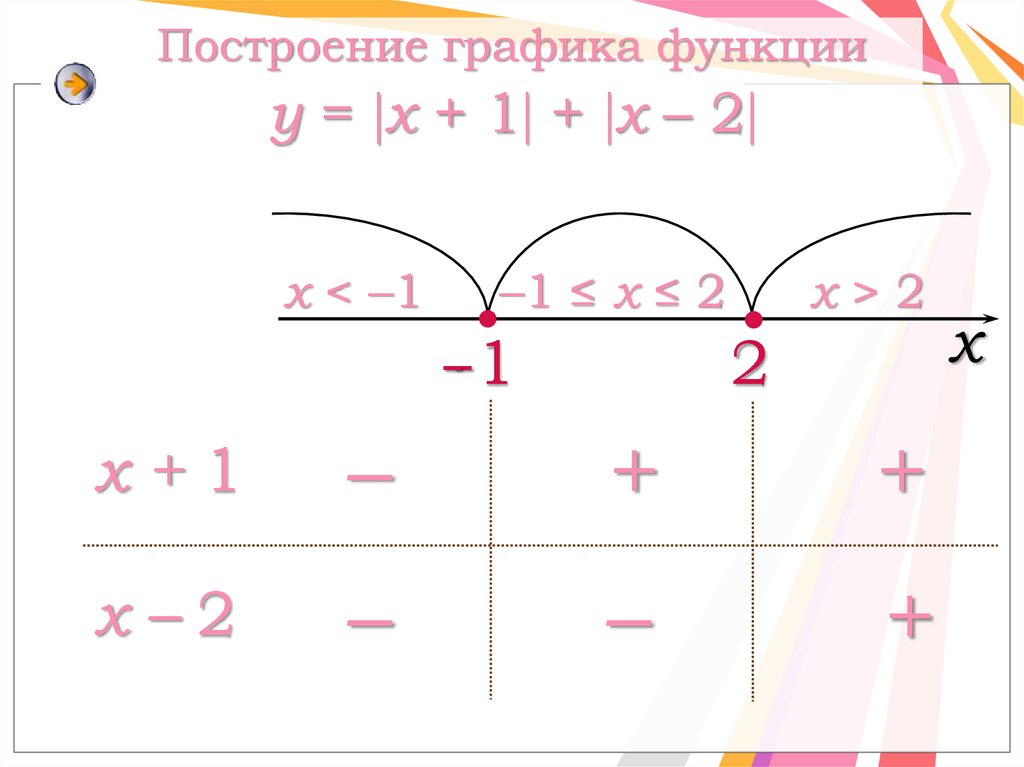
Построение графика функцииy = x + 1 + x – 2
x < –1
–1 ≤ x ≤ 2
--1
x>2
2
x+1
–
+
+
x–2
–
–
+
x
25.
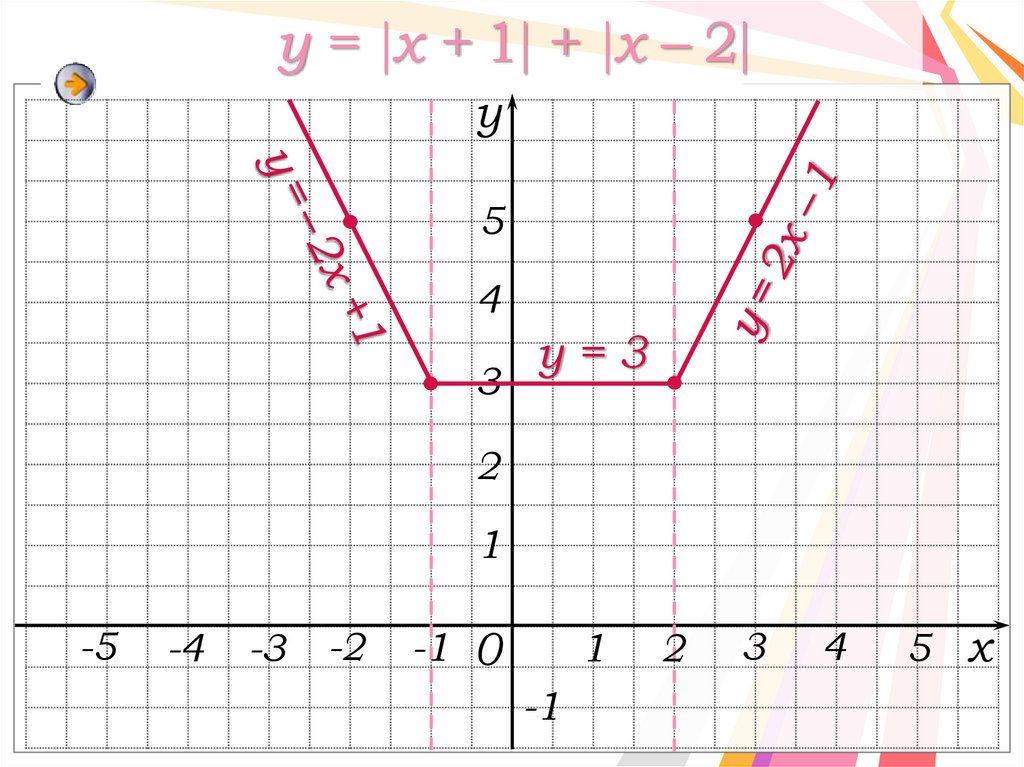
Построение графика функцииy = x + 1 + x – 2
x 1,
y x 1 x 2;
1 x 2,
y x 1 x 2;
x 2,
y x 1 x 2;
⇔
x 1,
y 2x 1;
1 x 2,
y 3;
x 2,
y 2x 1.
26.
y = x + 1 + x – 2y
5
4
3
у=3
2
1
-5
-4
-3
-2
-1 0
1
-1
2
3
4
5 x















 Математика
Математика








