Гравитационное притяжение эллипсоидов

1.

Гравитационное притяжение эллипсоидов
1. Внутри сферы притяжения
нет.
Теорема о притягательных
силах сферических тел.
Если к отдельным точкам
сферической поверхности
направлены равные
центростремительные силы,
убывающие в отношении
квадратов расстояний до
этих точек, то частица,
помещенная внутри этой
поверхности, от таких сил ни
в какую сторону притяжения
Рис 1

2.

2. Притяжение вне сферы.
Теорема о притяжении вне
сферы:
При тех же предположениях
утверждаю, что частица,
находящаяся вне
сферической поверхности,
притягивается к центру
сферы с силою, обратно
пропорциональною квадрату
ее расстояния до центра
сферы.

3.

3.Гомеоиды
Теорема:
Сила притяжения внутри бесконечно тонкого гомеоида равна
нулю.
Рис 2

4.

4. Теорема Арнольда
Рассмотрим гладкую
поверхность М,
задаваемую
полиномиальным
уравнением f(x,y,z)=n.
Например, уравнение
поверхности степени 4.
Точка Р называется
внутренней по отношению
к поверхности, если
каждая прямая,
проходящая через Р,
пересекает М ровно n
раз.
Рис 3

5.

Теорема:
Сила притяжения, с которой
поверхность М действует на
точку Р равна нулю.
Рис 4

6.

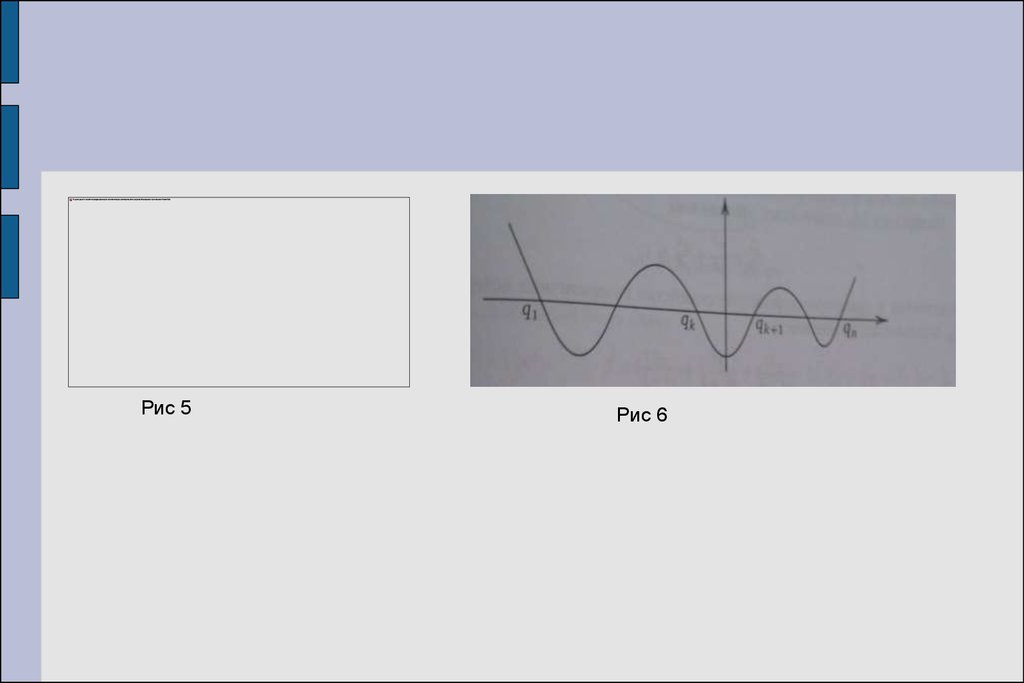
Рис 5
Рис 6

7.

(x− q1 )...( x− q n )
1
1
1
+ ¿
... ¿
=0
f (q 1) f ( q2 ) f (q n)
¿
f ¿( x)= ( x− q 2)... (x− qn )+ ( x− q1 )(x− q3 )...( x− q n)+ ( x− q 1)(x− q 2)...(x− q n− 1 )= 0
1
1
1
+
+ ...+
=0
(q n− q 2)(q n− q 3)... (q n− qn ) (q n− q1 )(q n− q3 )...(qn− q n )
(q n− q1 )...(qn− q n− 1)

8.

x2 y2 z2
+ + =1
a2 b2 c2
x2
y2
z2
+
+
=1
a 2 + ƛ b 2 + ƛ c 2+ ƛ
̀a b̀
c̀
A:( x , y , z ) →( X , Y , Z )= ( x , y , z)
a b
c
á = √a 2 + ƛ
́ √b2+ ƛ
b=
ć = √c 2+ ƛ