Похожие презентации:
Найпростіші геометричні фiгури та їх властивості. Тема 1. Геометричні фігури. Точки і прямі. Урок №1
1.
Тема 1. НАЙПРОСТІШІ ГЕОМЕТРИЧНІ ФIГУРИ ТАЇХ ВЛАСТИВОСТІ
УРОК № 1
Геометричні фігури. Точки і прямі.
2.
Давньогрецький вченийЕвклід
(IV ст.до н.е.)
3.
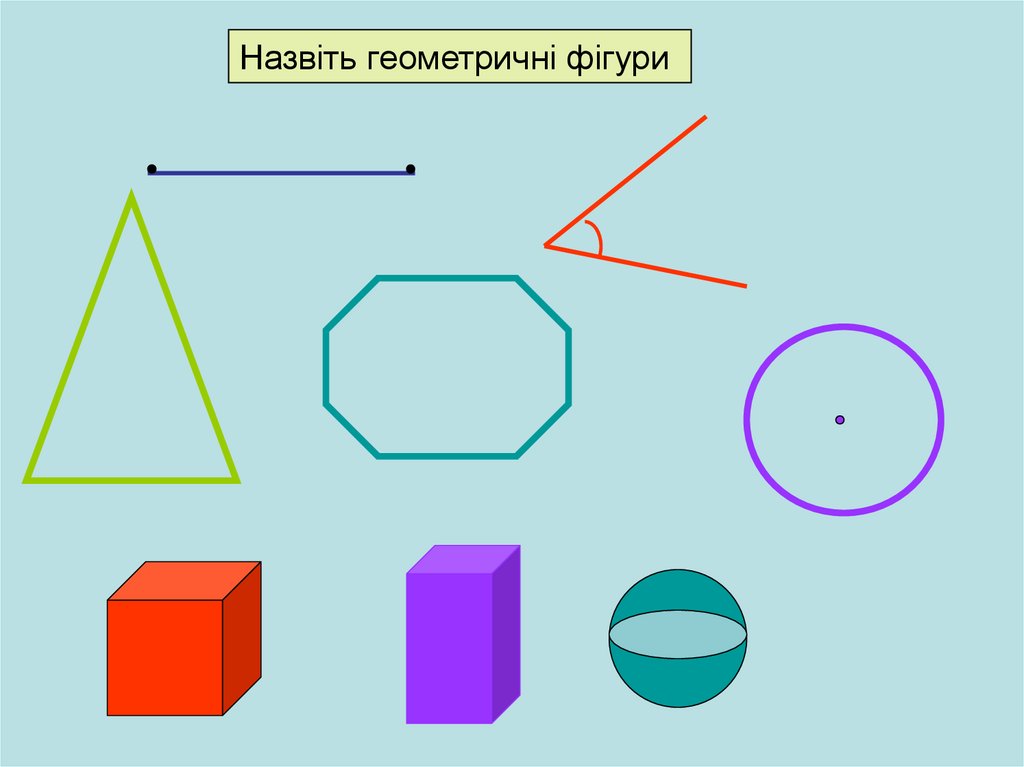
Назвіть геометричні фігури4.
АС
В
K
a
D
E
Яка б не була пряма , існують точки, що
належать цій прямій, і точки, що їй не належать
5.
аМ
А
N
в
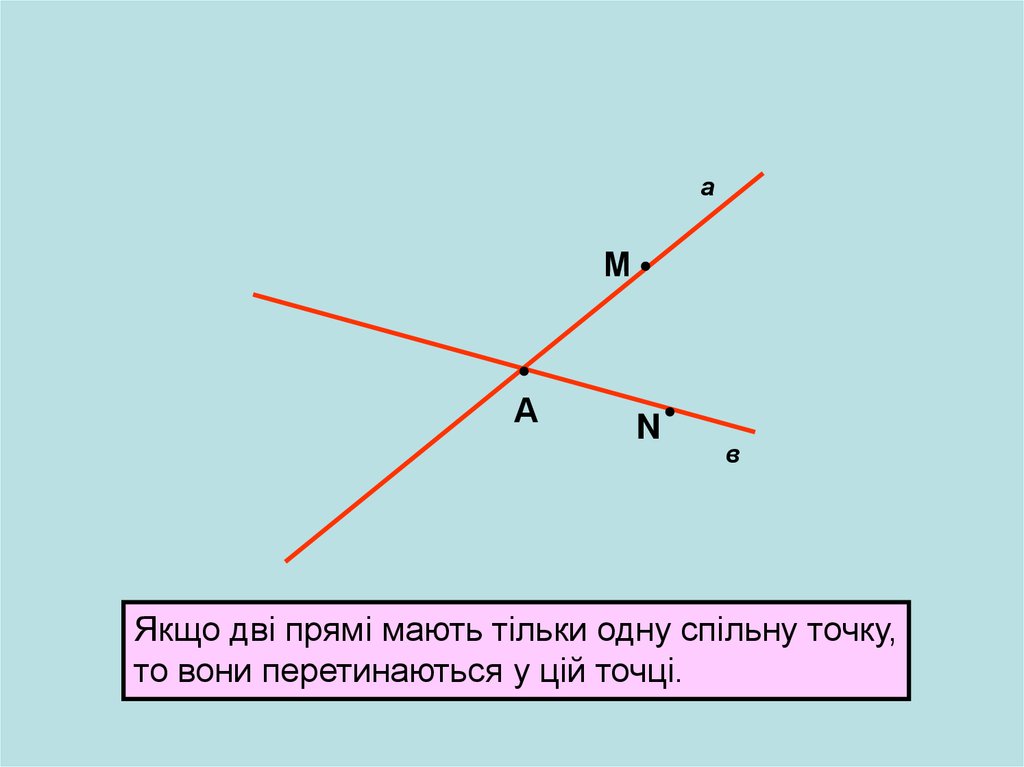
Якщо дві прямі мають тільки одну спільну точку,
то вони перетинаються у цій точці.
6.
АВ
Через будь-які дві точки можна провести пряму , і
тільки одну
7.
. .А
М
.
В
С
Р
N
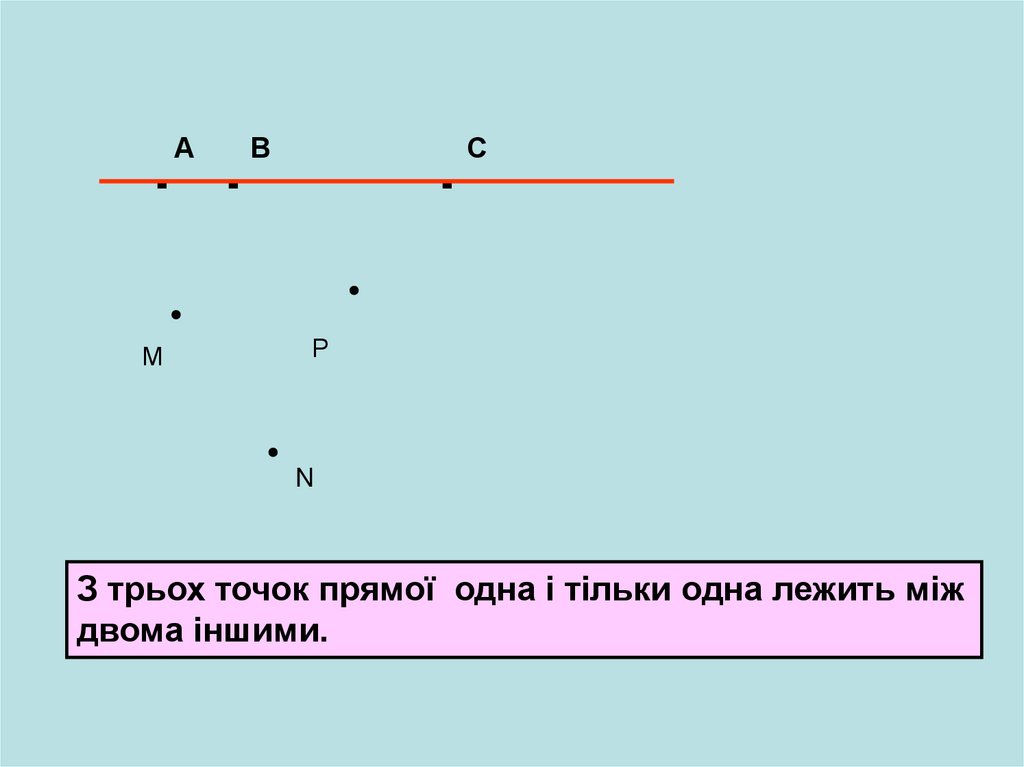
З трьох точок прямої одна і тільки одна лежить між
двома іншими.
8.
аА
К
А
О
В
Р
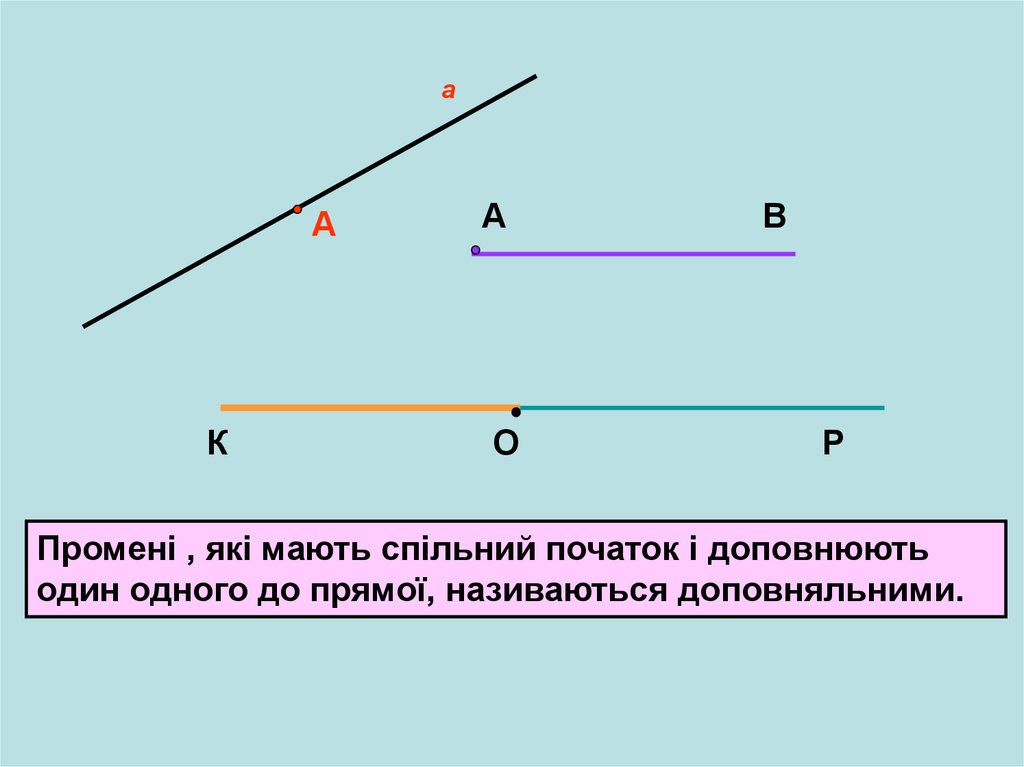
Промені , які мають спільний початок і доповнюють
один одного до прямої, називаються доповняльними.
9.
Розгляньте рисунок і дайте відповіді на запитання.Які прямі проходять через точку А, В, С і D?
На яких прямих лежать точки А, В, С і D?
У якій точці перетинаються прямі а і b, b і с, с і т, b і т?
У якій точці перетинаються три прямі? Назвіть ці прямі.
B
m
A
c
D
C
b
a
10.
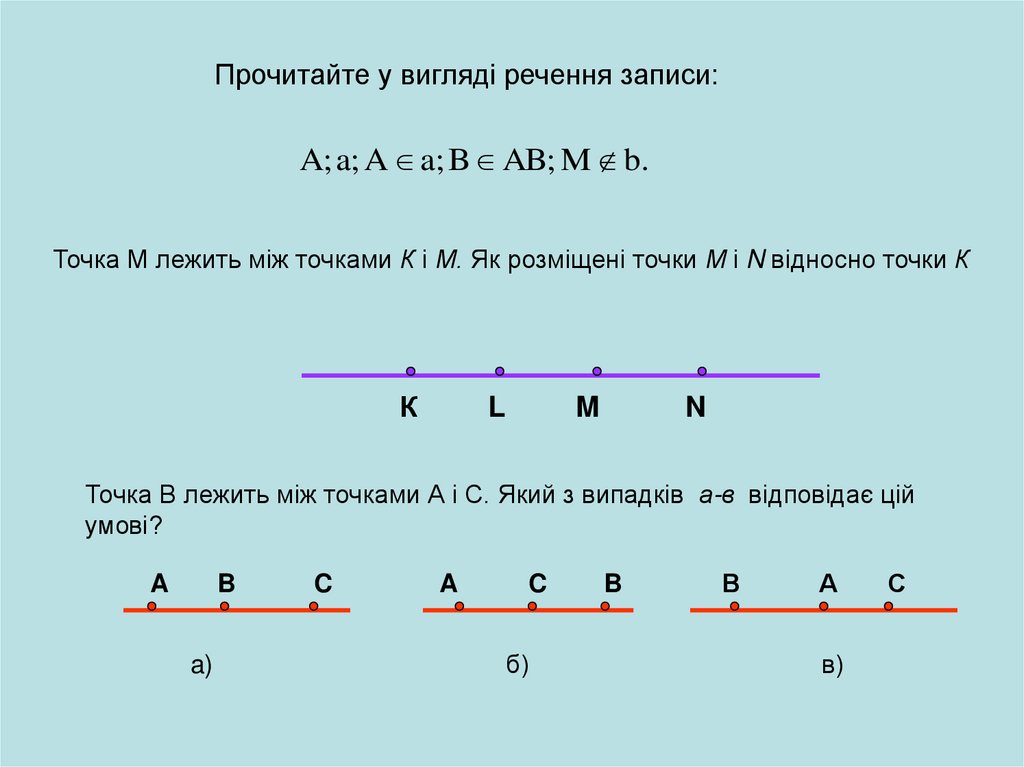
Прочитайте у вигляді речення записи:A; a; A a; B AB; М b.
Точка М лежить між точками К і М. Як розміщені точки М і N відносно точки К
К
L
M
N
Точка В лежить між точками А і С. Який з випадків а-в відповідає цій
умові?
A
B
a)
C
A
C
б)
B
В
А
в)
С
11.
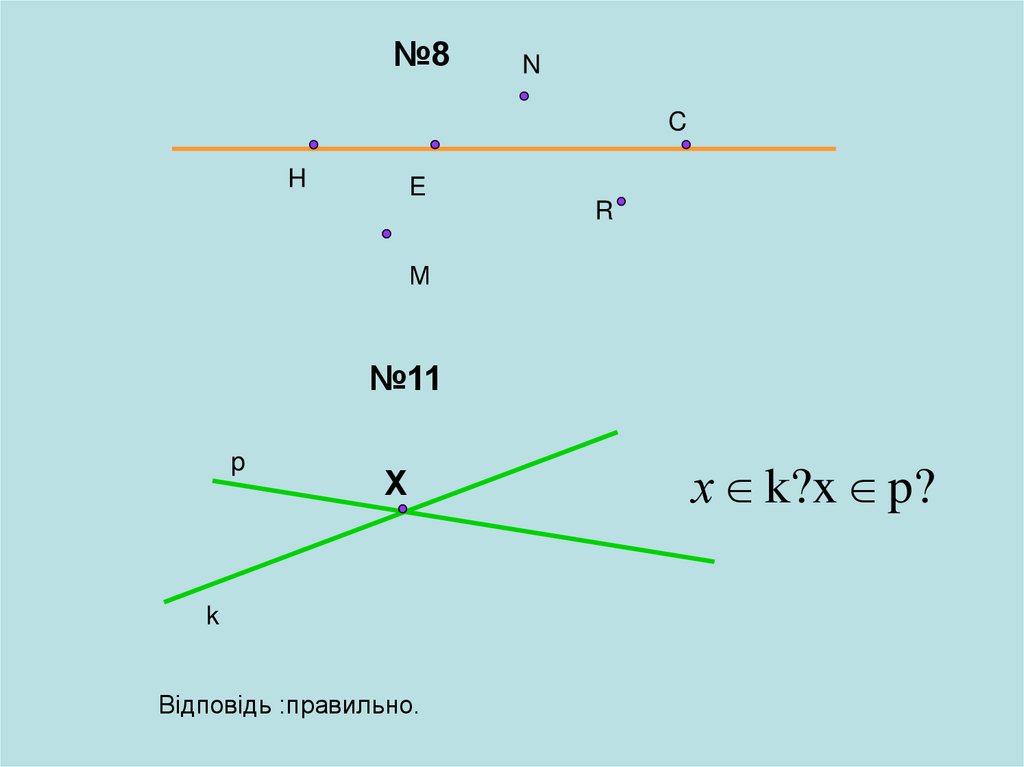
№8N
C
H
E
R
М
№11
p
Х
k
Відповідь :правильно.
х k?x p?
12.
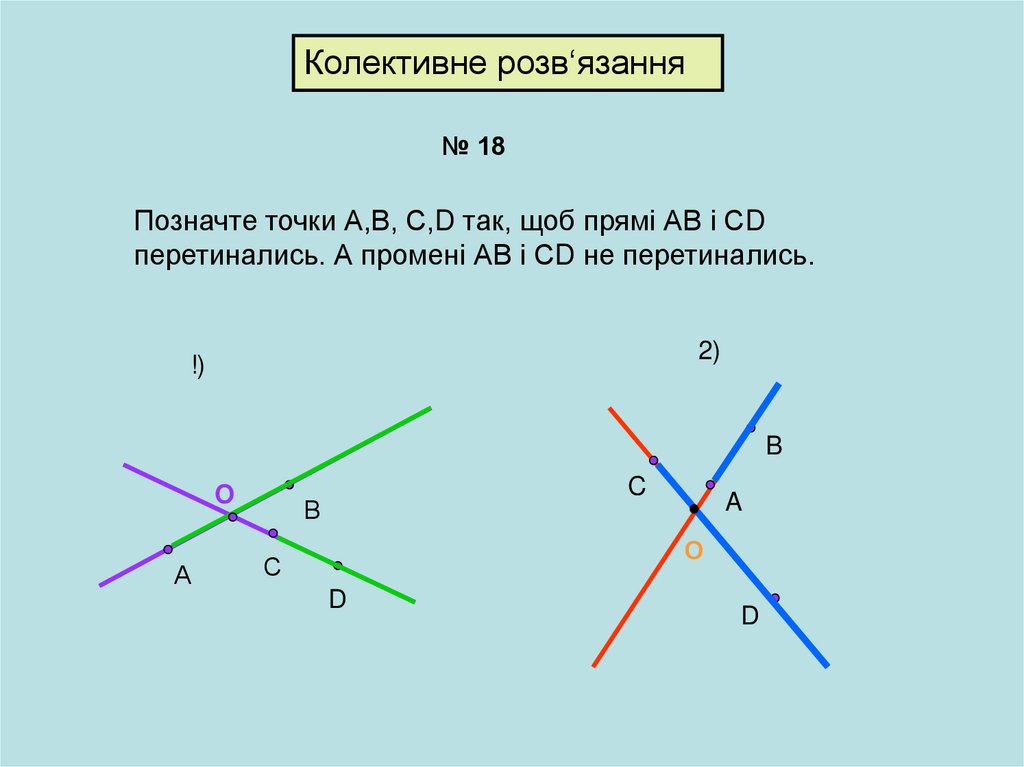
Колективне розв‘язання№ 18
Позначте точки А,В, С,D так, щоб прямі АВ і СD
перетинались. А промені АВ і СD не перетинались.
2)
!)
B
O
А
C
В
A
О
С
D
D
13.
Закінчити речення1.Геометрія вивчає…
геометричні фігури та їх властивості.
2.Планіметрія вивчає…
плоскі фігури.
3.Фігури,які можна розмістити в одній площині називаються…
4.Яка б не була пряма існують…
5.Трикутник – це…
6. Куб – це….
плоскими
точки, що належать цій прямій і
точки, що їй не належать.
плоска фігура.
неплоска фігура.
7.Через будь-які дві різні точки… можна провести пряму і тільки одну.
8.Два промені із спільним початком і доповнюють один одного до прямої
називаються… доповняльними.
14.
Геометрія є пізнаннявсього існуючого (IV ст.
до н. е.).
Платон
Платон
(древньогрецький філософ)







 Математика
Математика








