Похожие презентации:
Напряженно-деформированное состояние элемента материала
1.
Напряженнодеформированное состояниеэлемента материала
2.
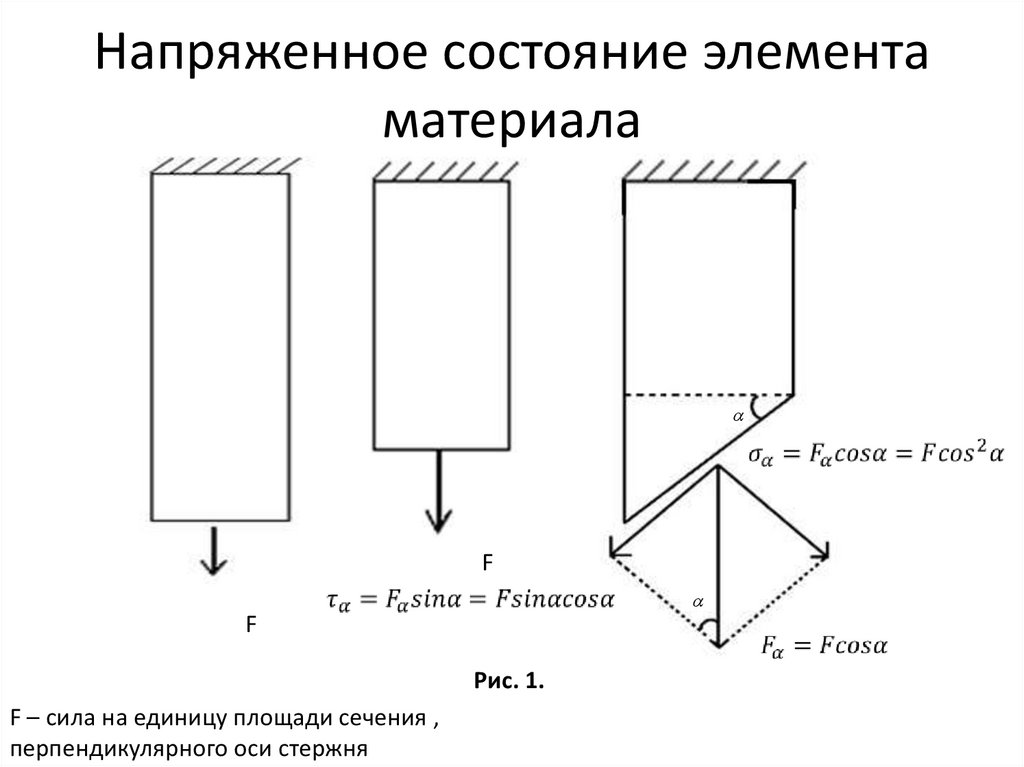
Напряженное состояние элементаматериала
F
F
Рис. 1.
F – сила на единицу площади сечения ,
перпендикулярного оси стержня
3.
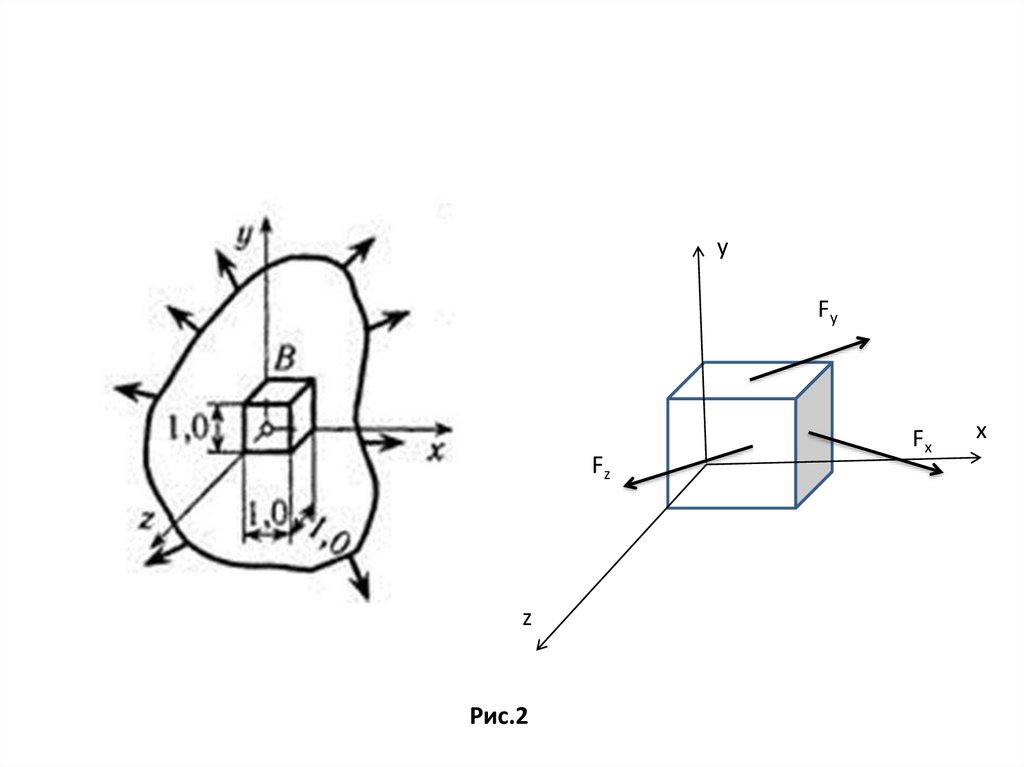
yFy
Fz
z
Рис.2
Fx
x
4.
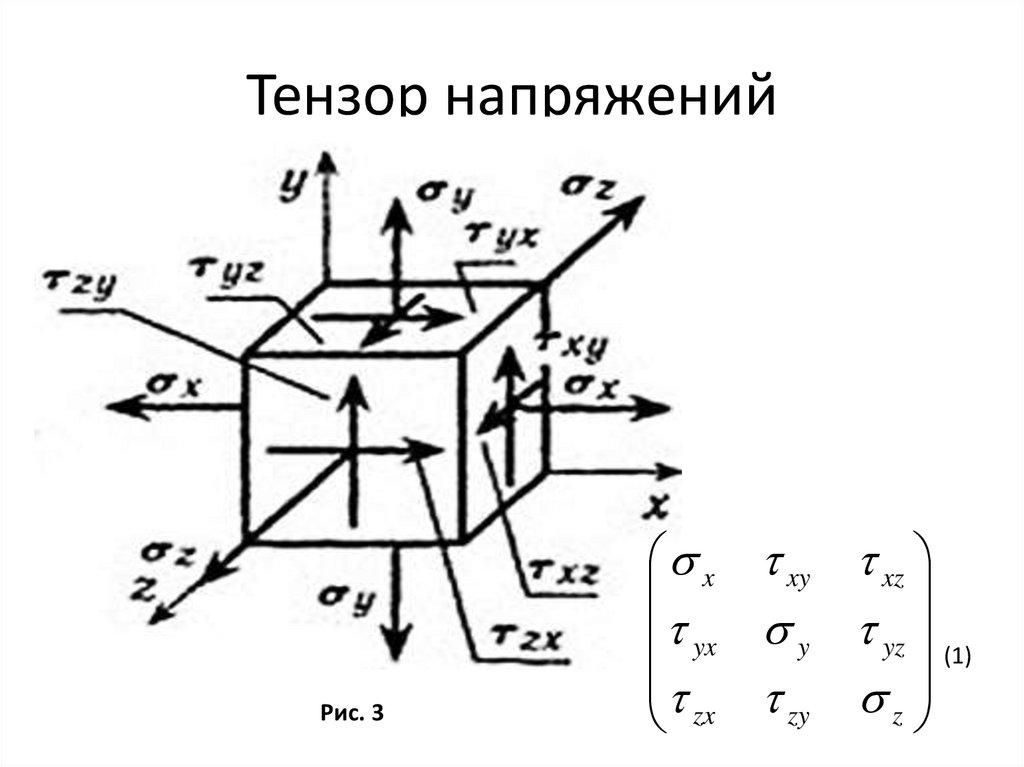
Тензор напряженийРис. 3
x xy xz
yx y yz (1)
zx zy z
5.
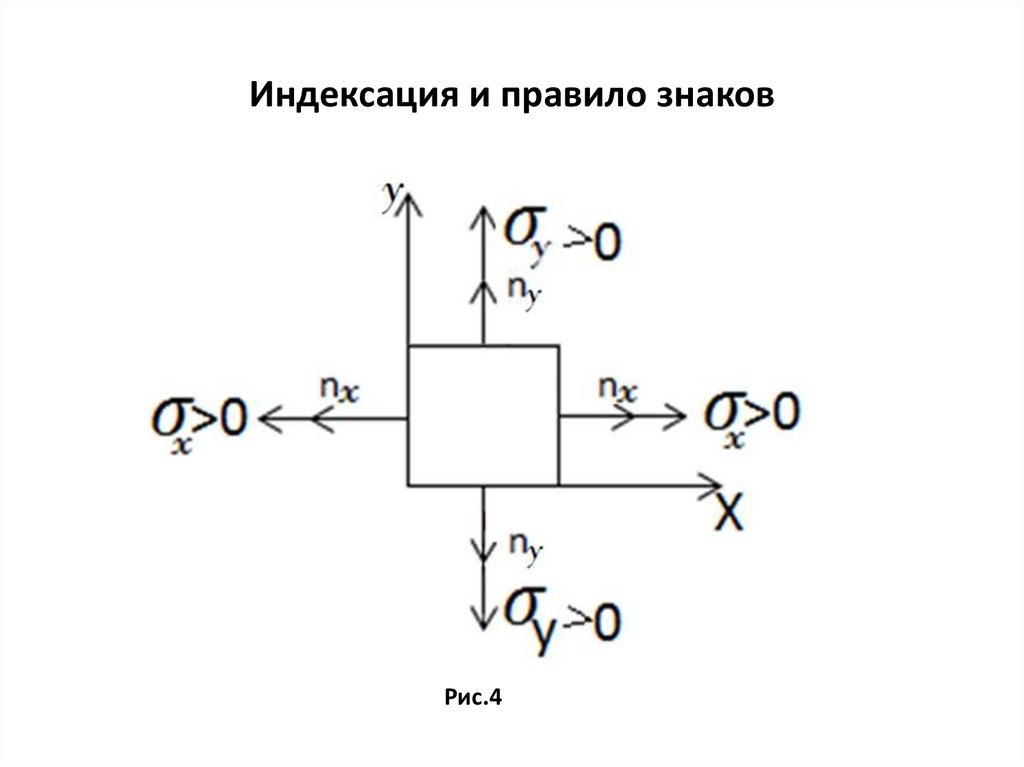
Индексация и правило знаковРис.4
6.
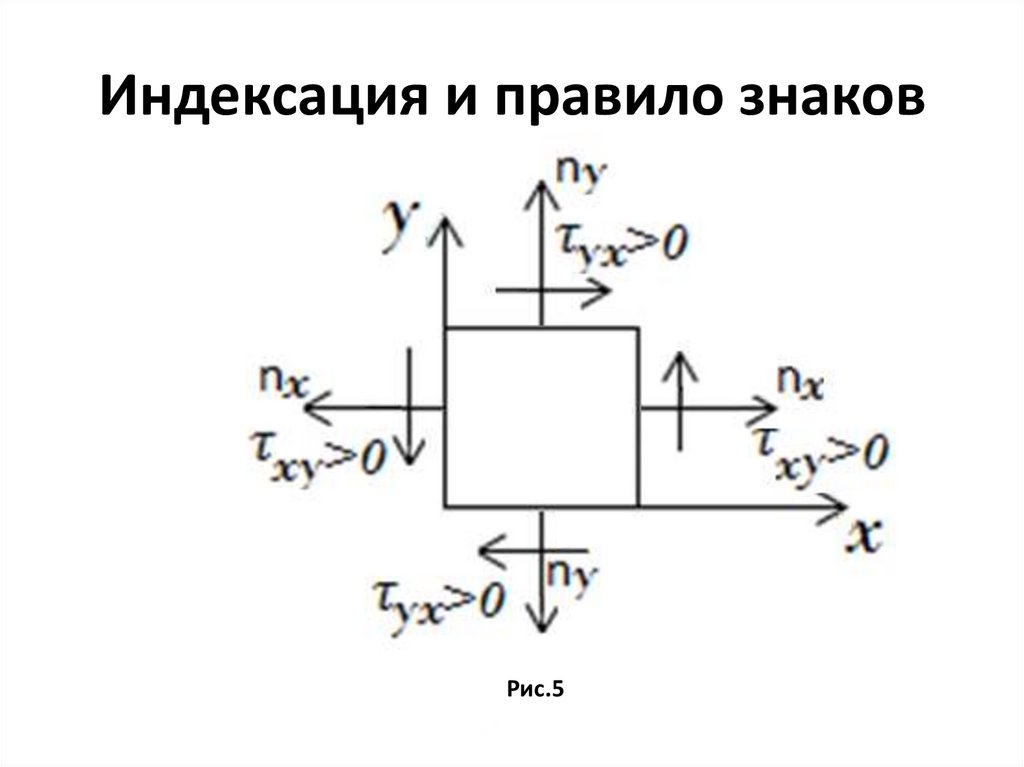
Индексация и правило знаковРис.5
7.
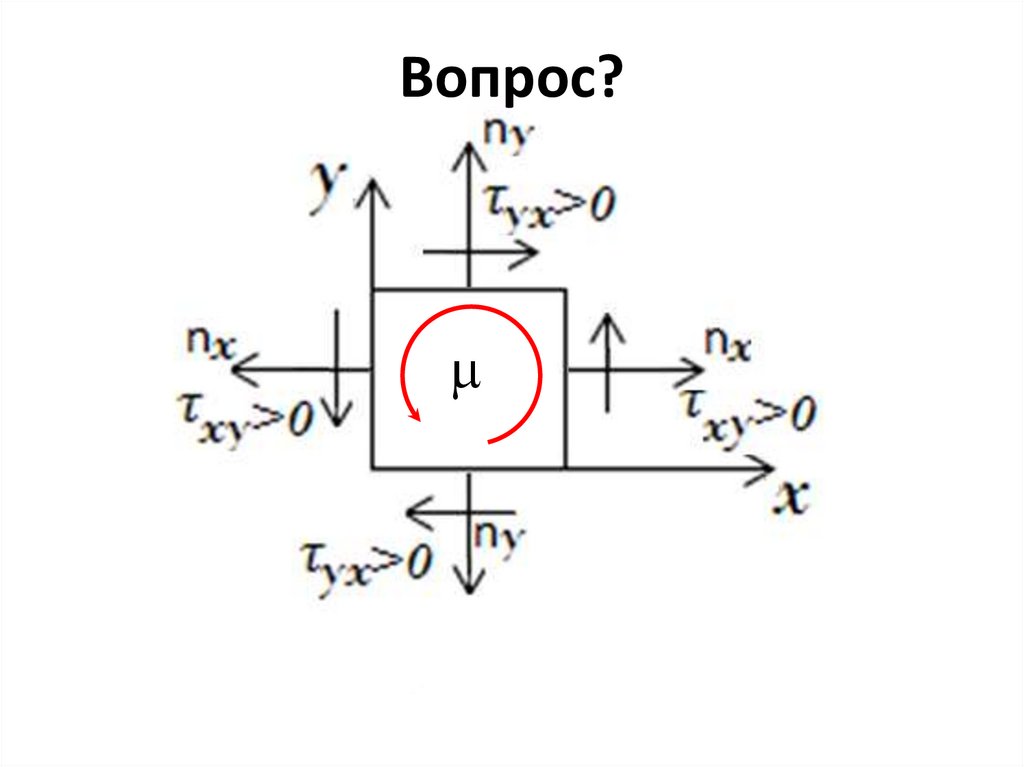
Вопрос?m
8.
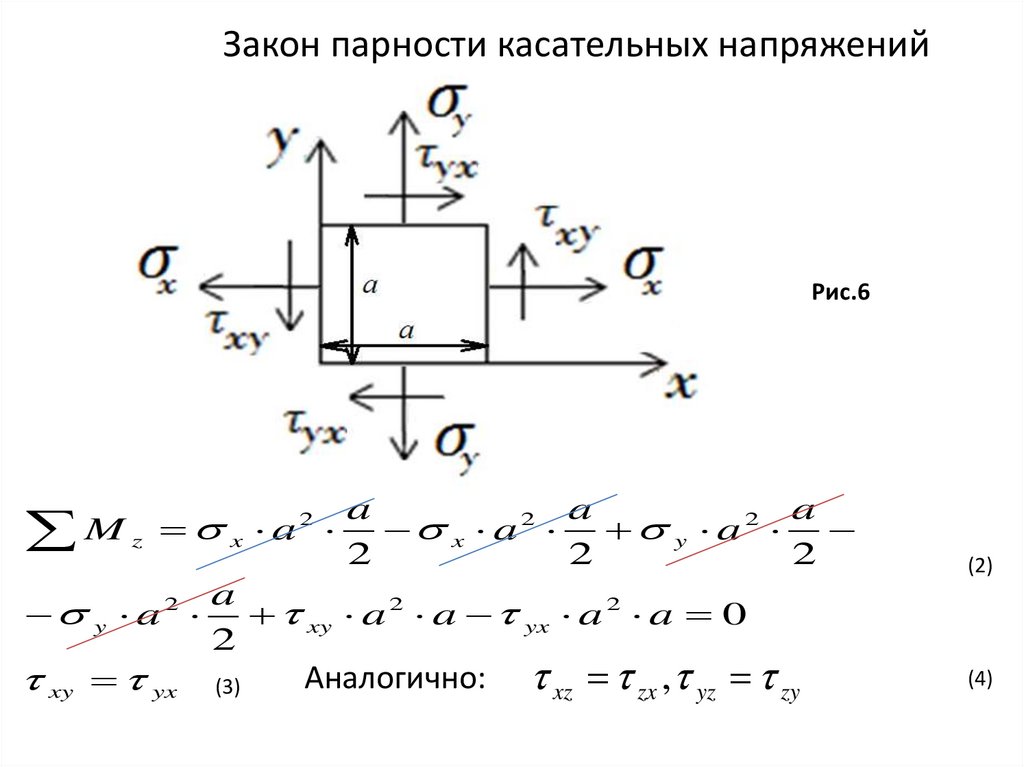
Закон парности касательных напряженийРис.6
2
M
a
z
x
y a2
xy yx
a
a
a
x a2 y a2
2
2
2
(2)
a
xy a 2 a yx a 2 a 0
2
(3)
Аналогично:
xz zx , yz zy
(4)
9.
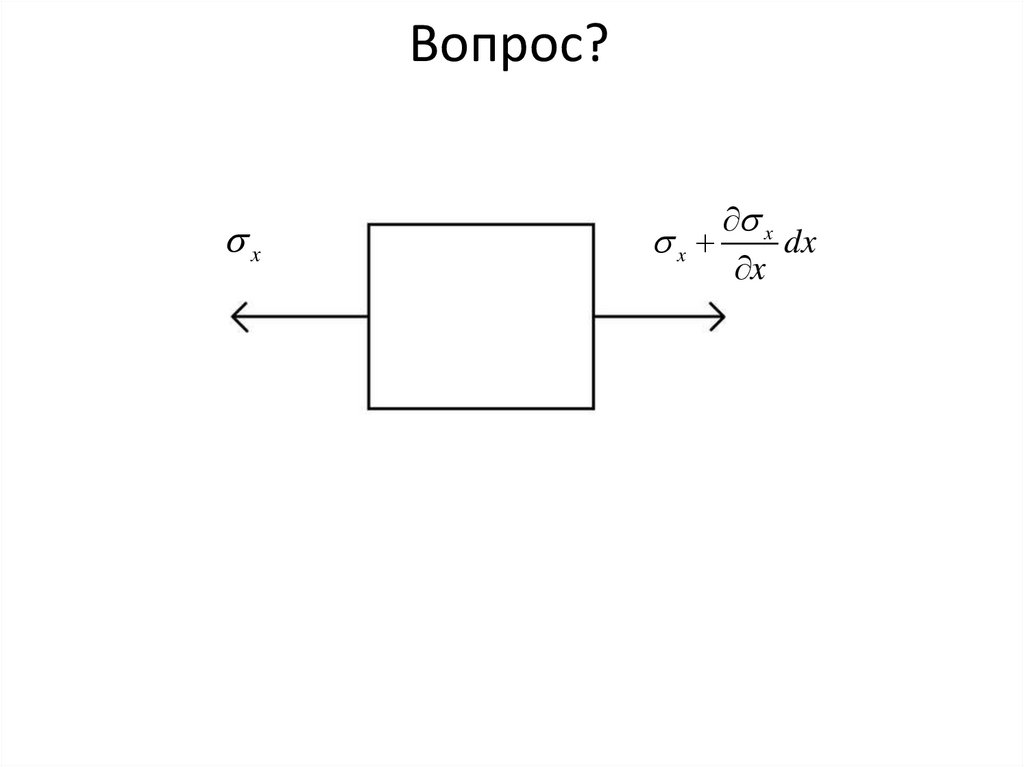
Вопрос?x
x
x
dx
x
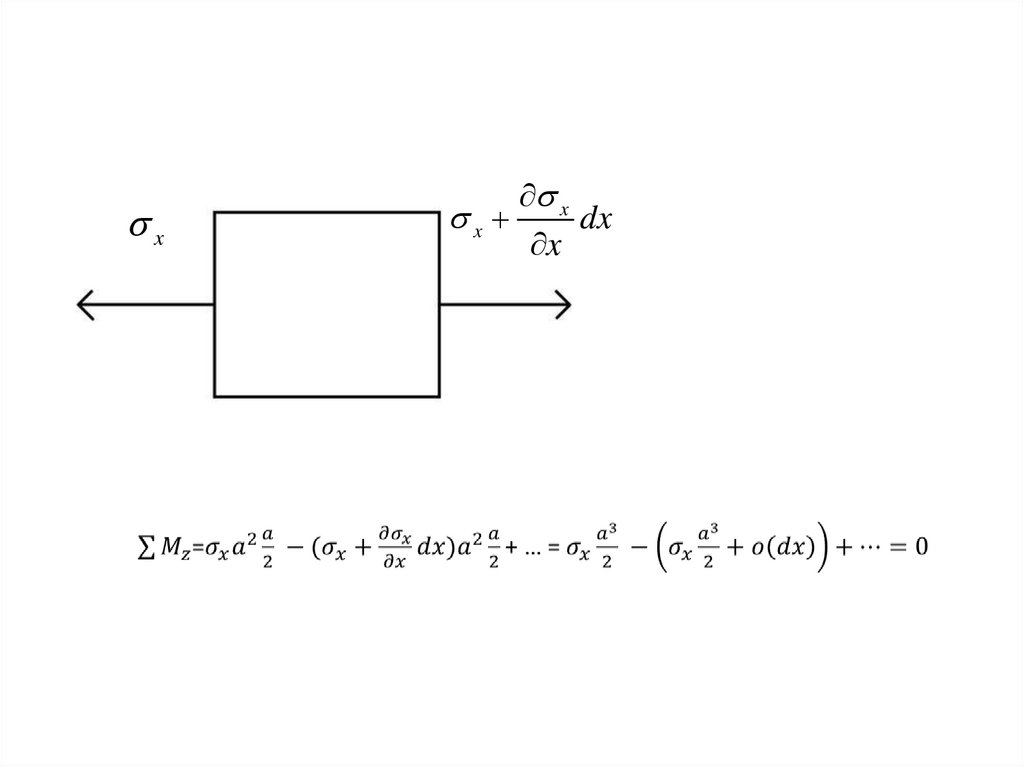
10.
xx
x
dx
x
11.
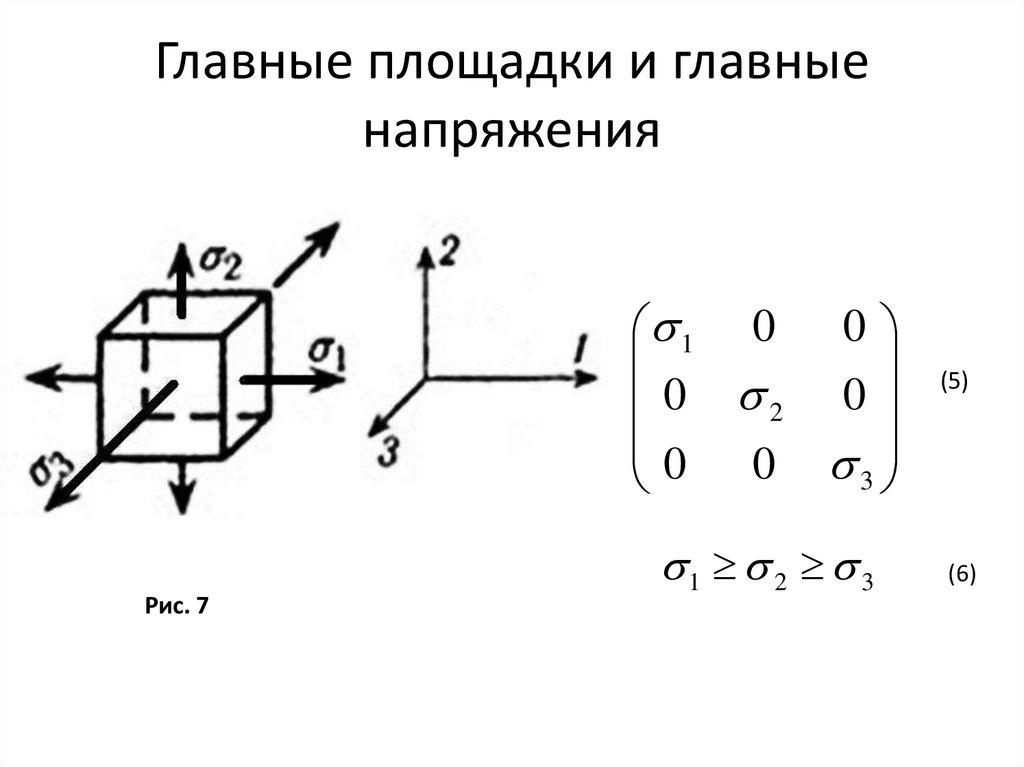
Главные площадки и главныенапряжения
1 0 0
0 2 0
0 0
3
Рис. 7
1 2 3
(5)
(6)
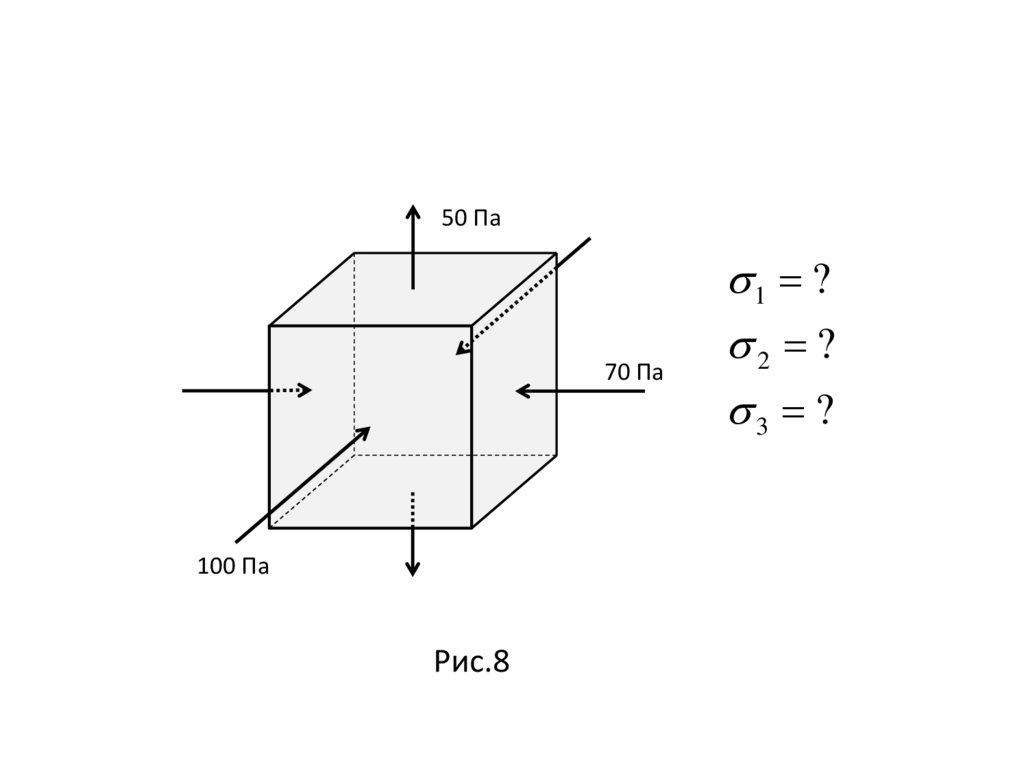
12.
50 Па70 Па
100 Па
Рис.8
1 ?
2 ?
3 ?
13.
Плоское напряженное состояниеРис. 9
14.
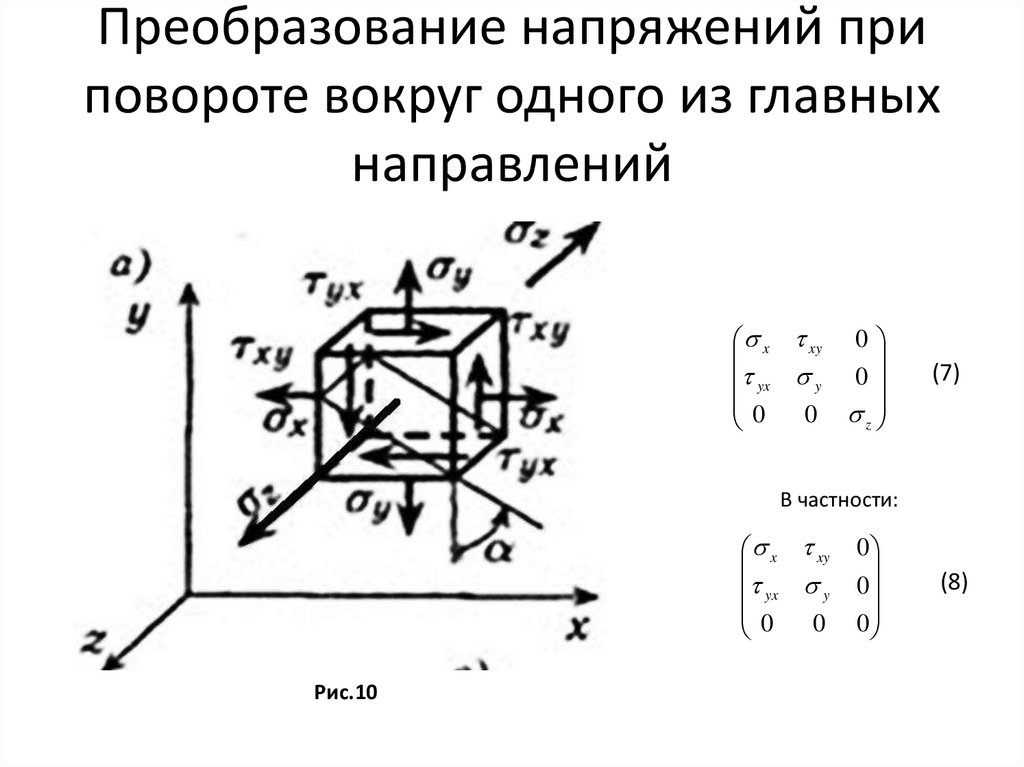
Преобразование напряжений приповороте вокруг одного из главных
направлений
x xy 0
0
yx
y
0
0 z
(7)
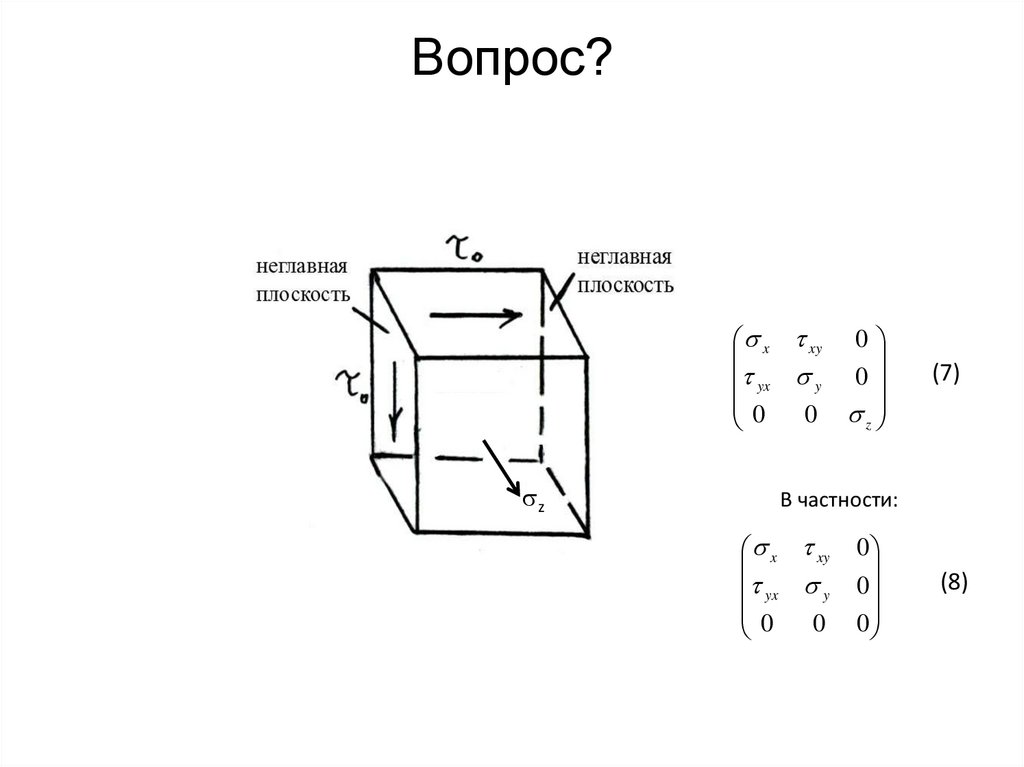
В частности:
x xy
yx y
0
0
Рис.10
0
0
0
(8)
15.
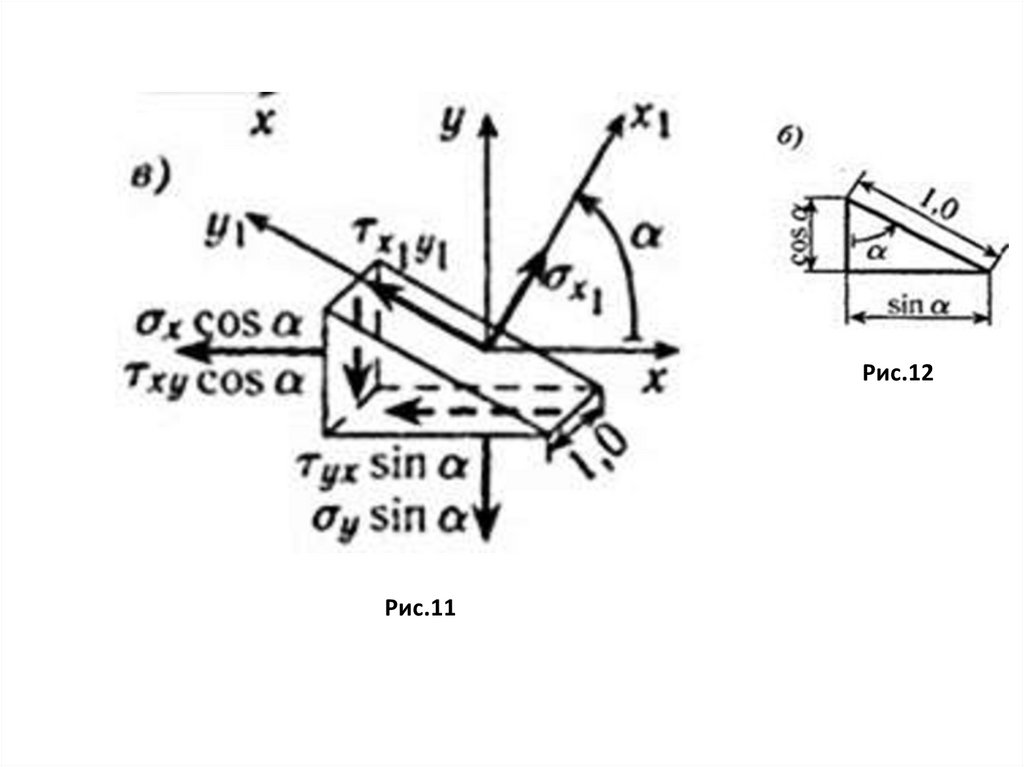
Рис.12Рис.11
16.
1. Переход от неглавных площадок к другимнеглавным площадкам
Рис.13
Проекции сил на оси X₁ ,Y₁
(9 )
17.
С учетом:xy yx ; 2 sin cos sin 2 ; cos 2 sin 2 cos 2
sin (1 cos 2 ) / 2; cos (1 cos 2 ) / 2
2
2
1
1
x1 2 x y 2 x y cos 2 xy sin 2
1 sin 2 cos 2
x
y
xy
x1 y1
2
(10)
(11)
(12)
18.
y1
1
x y 1 x y cos 2 xy sin 2
2
2
(12) ⇒
(13 )
tg 2
2 xy
x y
(11) + (13)=> x y x1 y1 - первый инвариант
тензора напряжений
В трехмерном случае x y z x1 y1 z1
(14 )
(15)
19.
2.Переход от главных площадок кнеглавным
xy 0
(16)
(11), (12), (13) =>
1
1
x1 2 1 2 2 1 2 cos 2
1
1
y1 1 2 1 2 cos 2
2
2
1
x1 y1 2 1 2 sin 2
(17)
(18)
(19)
(17)+(18)=>(20)
x y 1 2
1
1
Первый инвариант тензора напряжений
(20)
20.
Условие экстремальности и главныенапряжения
Условие экстремальности
(21)
(22)
(23)
21.
3.Нахождение главных площадок ивычисление главных напряжений
17 18 (24) x y 1 2 cos 2
(24)
2 (19) (25)
2 x1 y1 1 2 sin 2
(25)
(24) 25 26
x y 4 xy 2 1 2
1
2
1
2
2
1
2
(26)
1
1 2 ( x y )2 4 x2 y
(27)
1 2 x y
(20`)
1
1
1
1 1
1
(20`)±(27)=>(28)
1
1, 2 ( x1 y1 ) ( x1 y1 )2 4 x21 y1
2
(28)
22.
1*
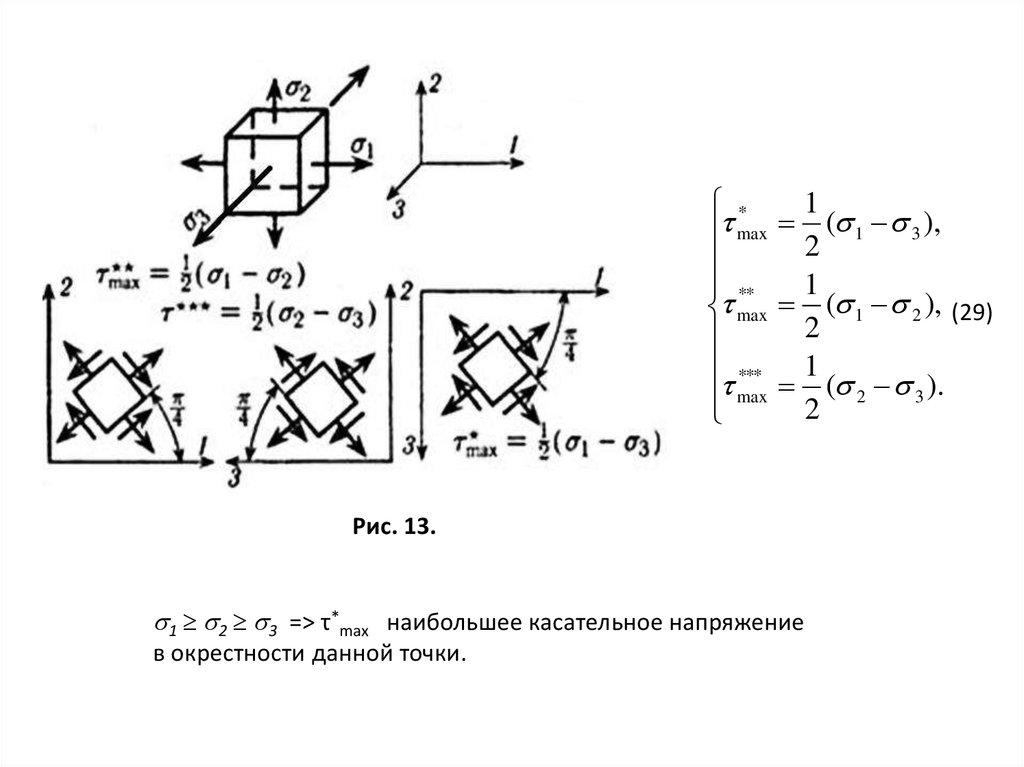
max 2 ( 1 3 ),
1
**
max ( 1 2 ), (29)
2
*** 1
max 2 ( 2 3 ).
Рис. 13.
1 2 3 => τ*max наибольшее касательное напряжение
в окрестности данной точки.
23.
Аналогичные результаты получаются (МТДТ, МКЭ) умножением тензоранапряжений σ на матрицу поворота R. Тензор напряжений в данном случае:
x xy 0
σ xy y 0
0
0 z
(30)
Матрица поворота на угол α вокруг оси z:
cos
R sin
0
sin
cos
0
0
0
1
(31)
Поворот тензора напряжений осуществляется по следующему правилу:
cos
σ* RσR T sin
0
sin
cos
0
0 x xy 0 cos
0 xy y 0 sin
1
0 z
0
0
sin
cos
0
0
0
1
Умножение матриц выполняется по правилу, известному из курса
линейной алгебры:
(32)
24.
cosσ sin
0
sin
cos
sin
0
0
sin
xy
0
y
1 0
cos
*
0 x
xy
0 cos
sin
0
cos
sin
0
0
0
0 x cos xy sin
x sin xy cos
0
xy sin y cos
xy
y
2
2
xy
xy
y
2
x
xy
0
z
x sin cos xy cos xy sin y cos sin
2
2
x sin xy cos sin xy sin cos y cos
2
xy
(33)
0
0
cos sin cos cos sin sin
= cos sin sin cos sin cos
0
x
1
0
0
z
cos sin
1
0
cos
0
2
y
2
0
0
0
z
Используя применённые ранее тригонометрические соотношения приходим к тому
же результату
cos 2 sin 2
σ
sin 2 cos 2
0
1
2
*
12 x y x sin 2 xy cos 2
1
x
y
x
2
y
x
xy
1
2
x
y
x
xy
1
2
cos 2 sin 2
1
x
y
2
x
y
0
x
xy
0
(34)
0
z
25.
Альтернативное правило знаковРис.15
26.
11
x y cos 2 xy sin 2
x
x
y
1
2
2
1 sin 2 cos 2
y
xy
x1 y1 2 x
tg 2 0
2 xy
x y
1
1
1 2 cos 2
2
x 2 1
2
1
1
1 2 cos 2
y
1
2
2
2
1
xy 2 1 2 sin 2
(35)
(36)
(37)
(38)
(39)
(40)
27.
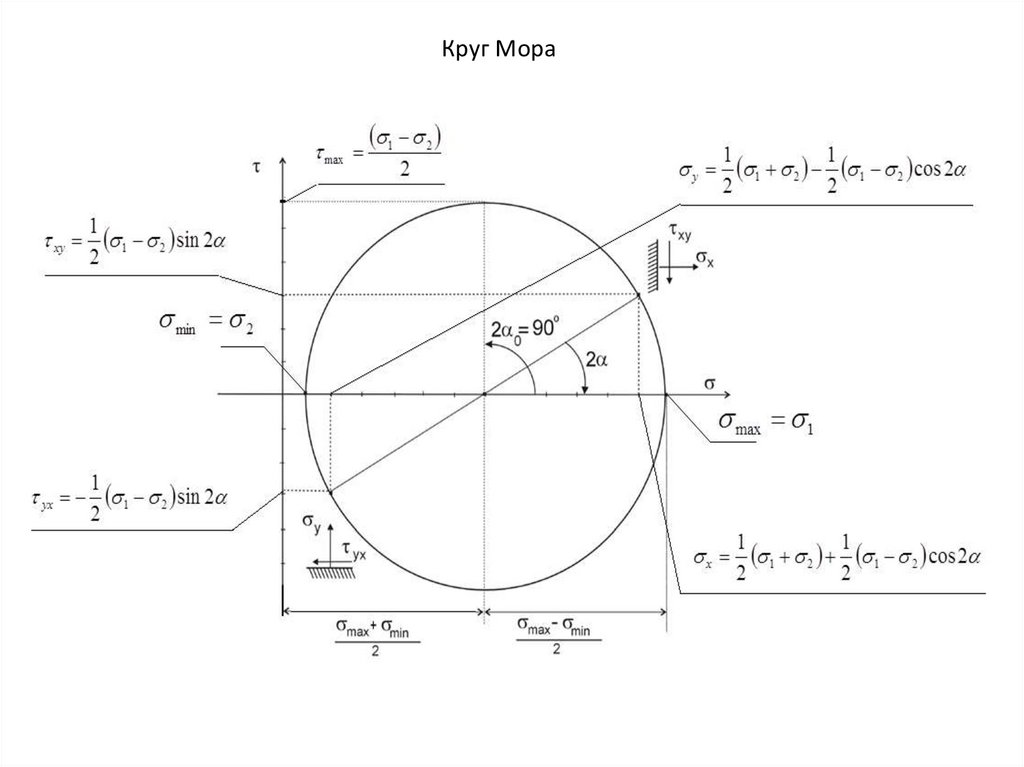
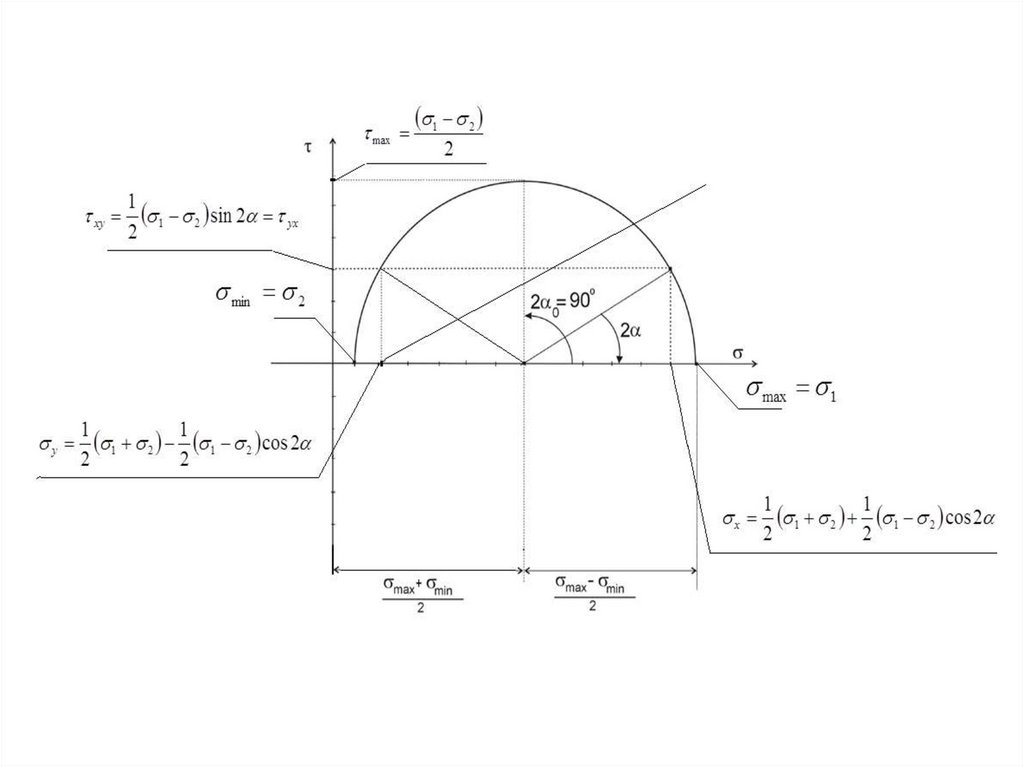
Круг Мора28.
(41)(11)-(13) =>
(14) =>
1
1
x1 2 x y 2 x y cos 2 xy sin 2
1
1
y1 x y x y cos 2 xy sin 2
2
2
1
x1 y1 2 x y sin 2 xy cos 2
tg 2
2 xy
(42)
(43)
x y
1
1
1 2 cos 2
2
x1 2 1
2
1
1
y1 1 2 1 2 cos 2
2
2
1
1 2 sin 2
x1 y1
2
(44)
29.
30.
Деформированное состояниеэлемента материала
(45)
(46)
(47)
Рис.18
31.
Рис.1932.
Тензор деформацииx
1
2 yx
1
zx
2
1
xy
2
y
1
zy
2
1
xz
2
1 =
yz
2
z
x
yx
zx
xy xz
y yz
zy z
33.
Аналогично формулам (Напр. состояние)(11),(12),(13)1
1
x1 2 x y 2 x y cos 2 xy sin 2
1
1
x y cos 2 xy sin 2
y1
x
y
2
2
1
x1 y1 2 x y sin 2 xy cos 2
Аналогично ( Напр. состояние ) (14)
tg 2 0
2 xy
x y
34.
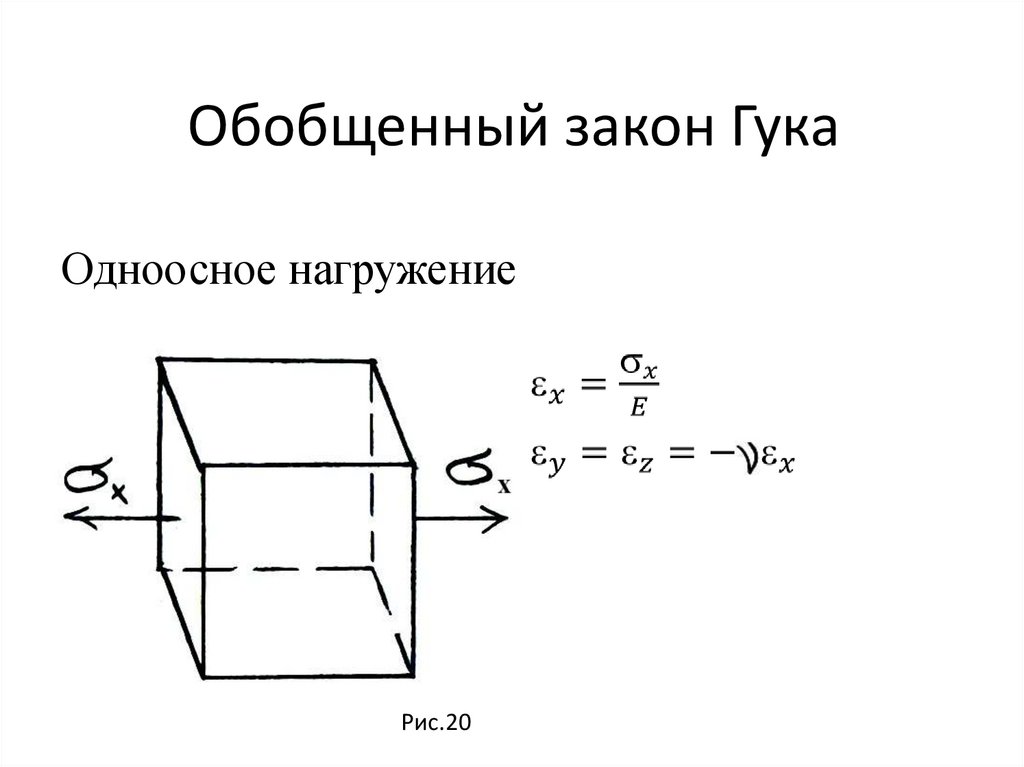
Обобщенный закон ГукаОдноосное нагружение
Рис.20
35.
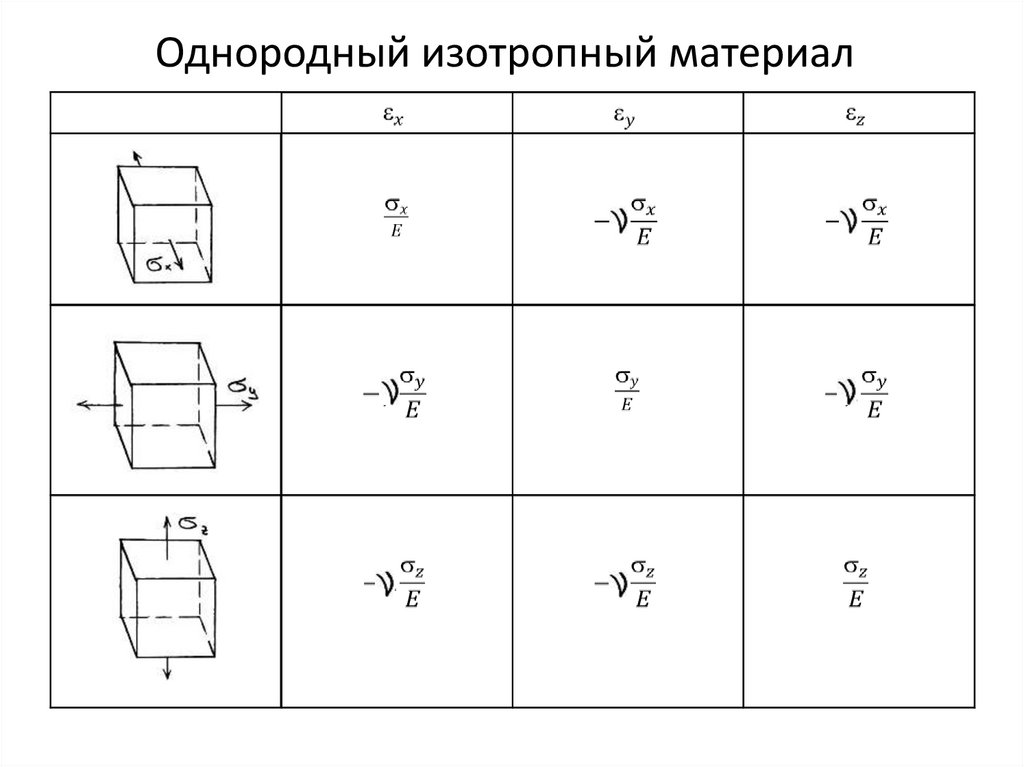
Однородный изотропный материал36.
37.
038.
0ν=0,5 соответствует ΔV=0
39.
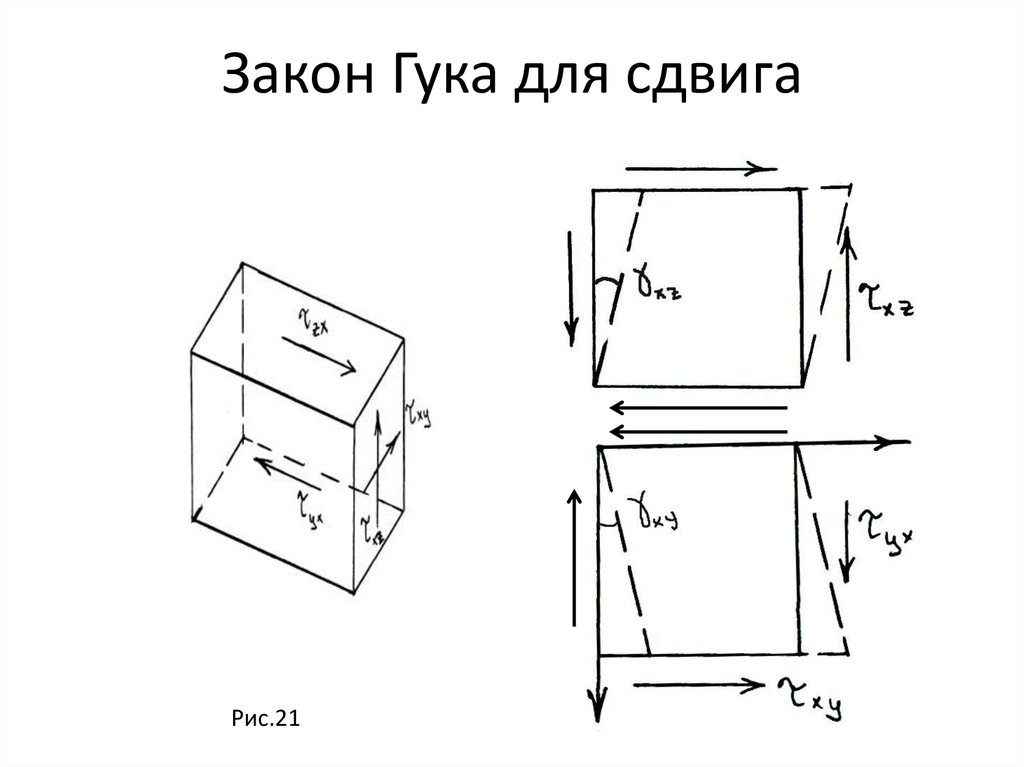
Закон Гука для сдвигаРис.21
40.
41.
Энергия упругой деформации U приодноосном нагружении



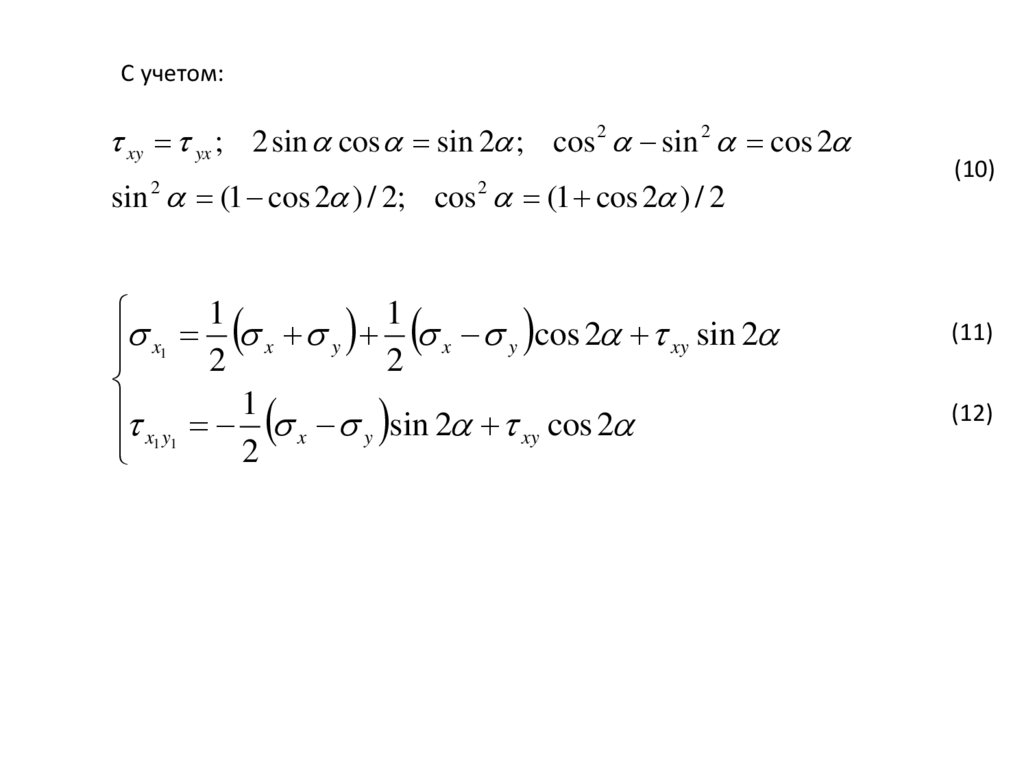







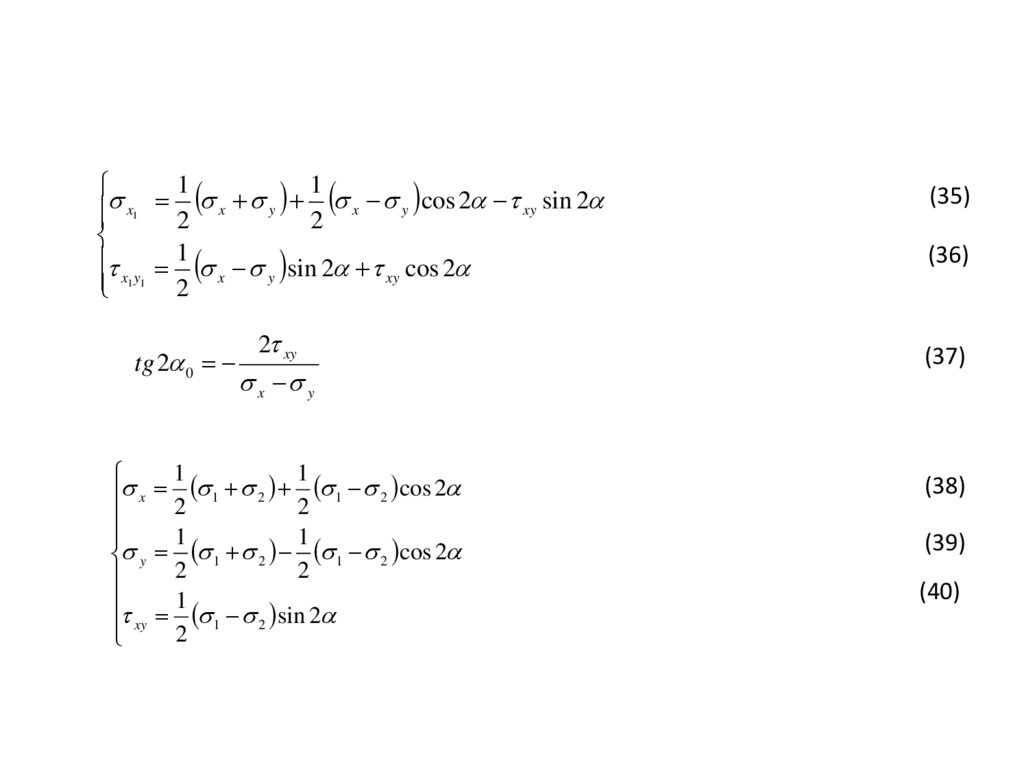
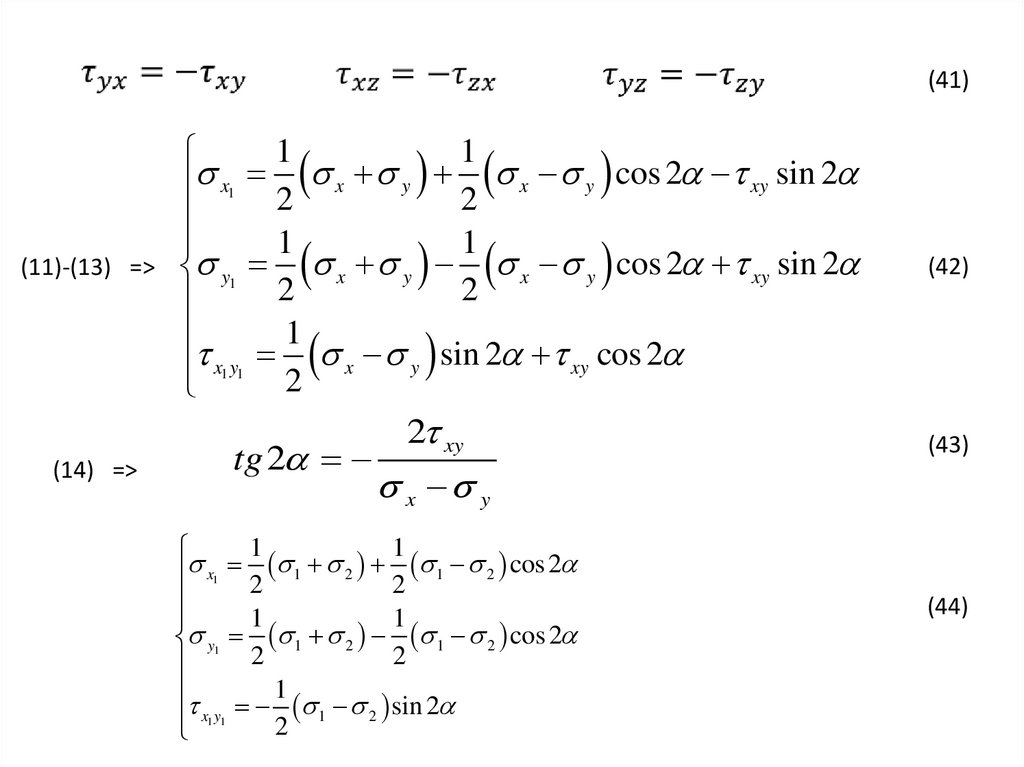




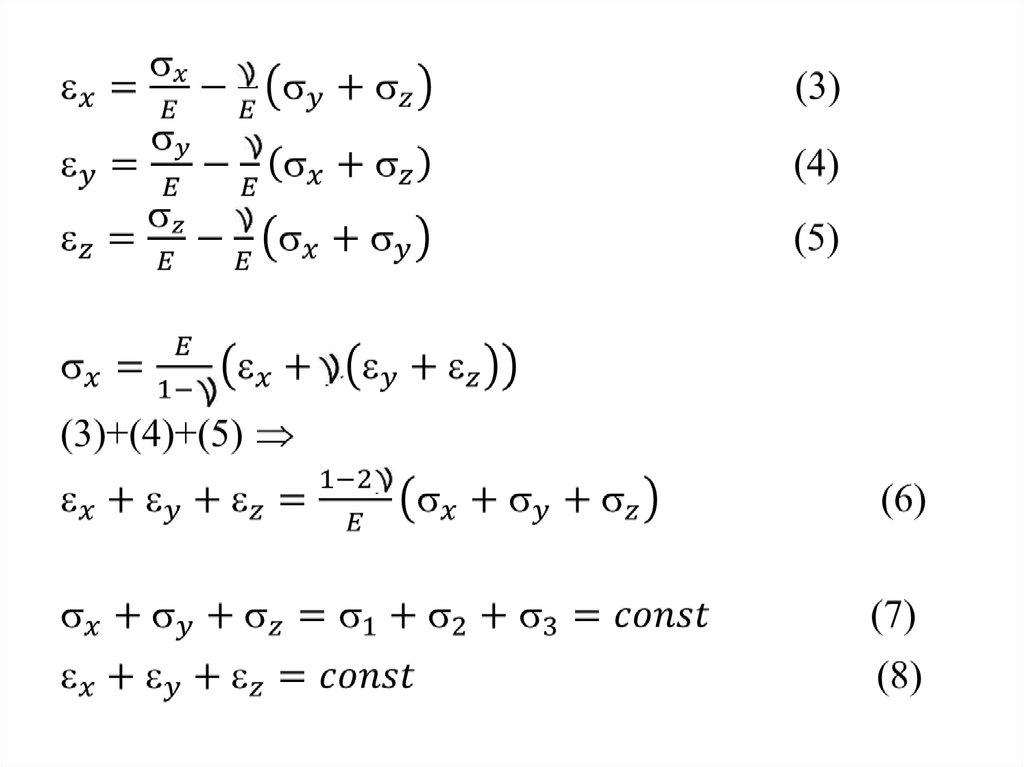
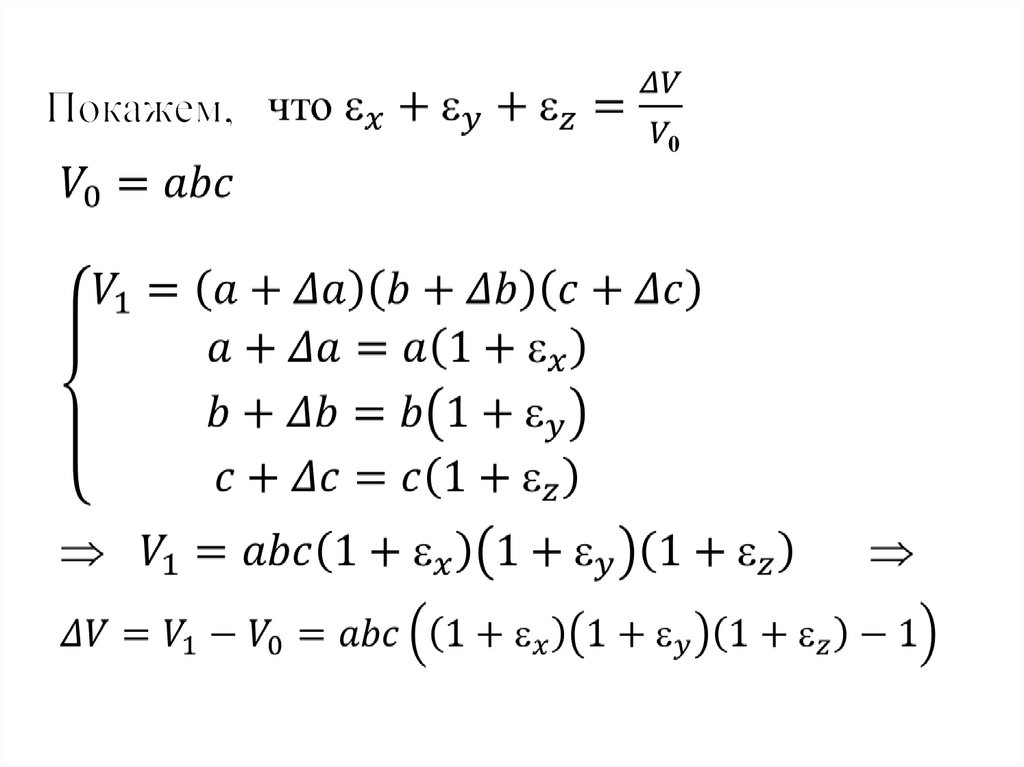



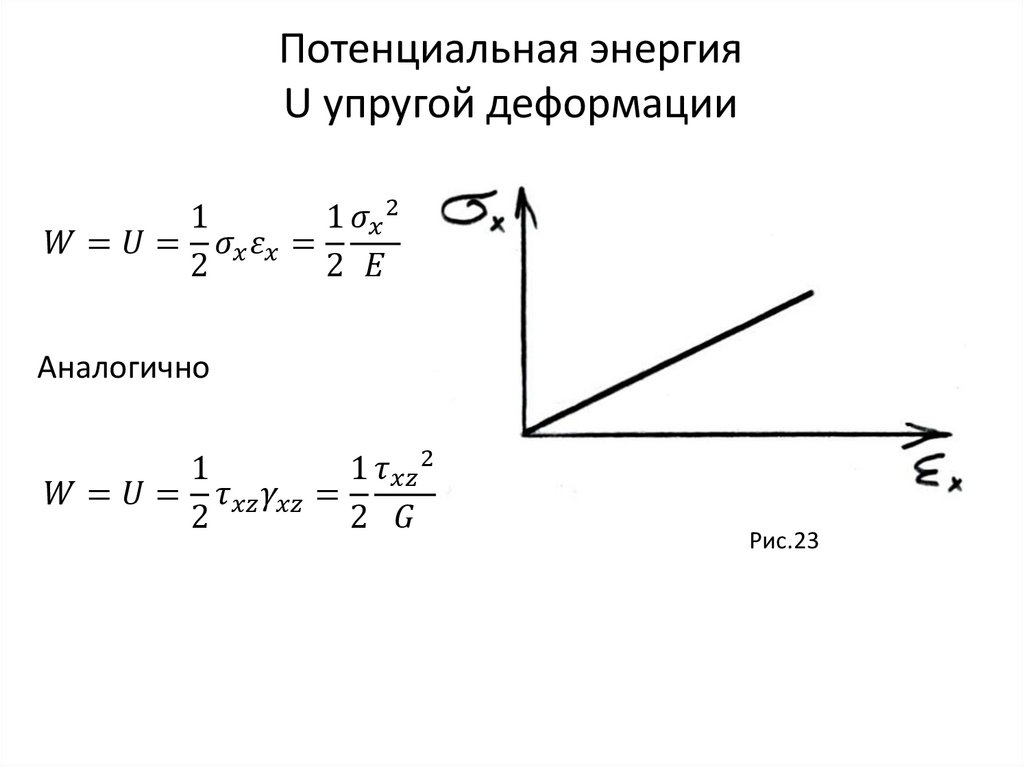
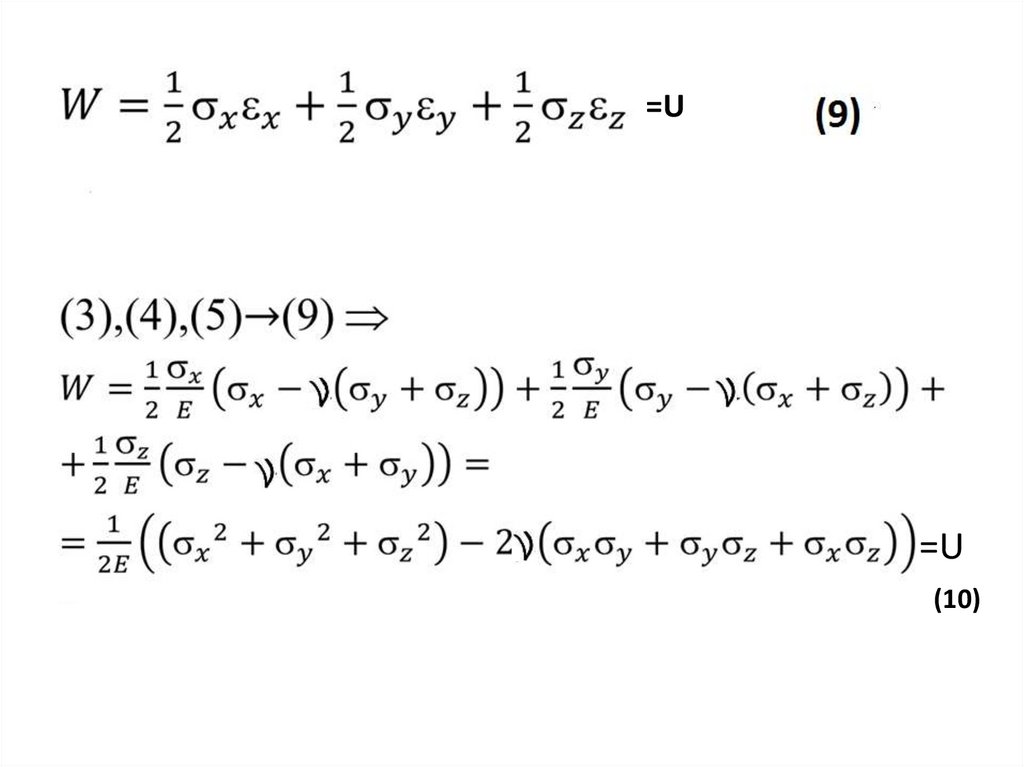
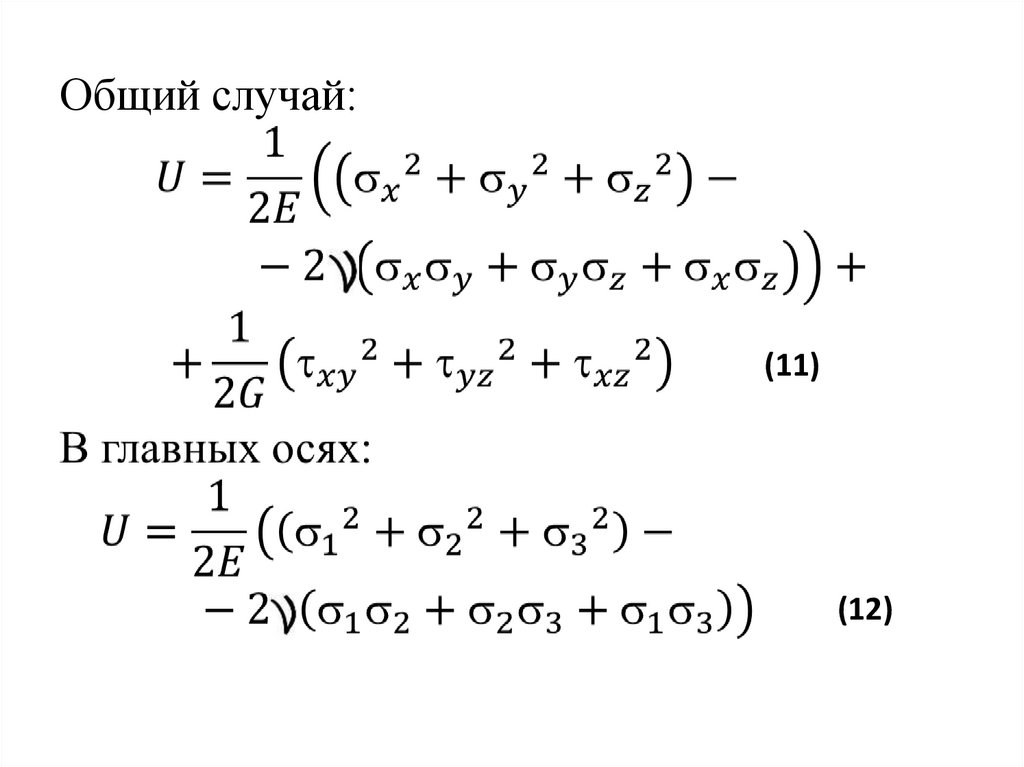
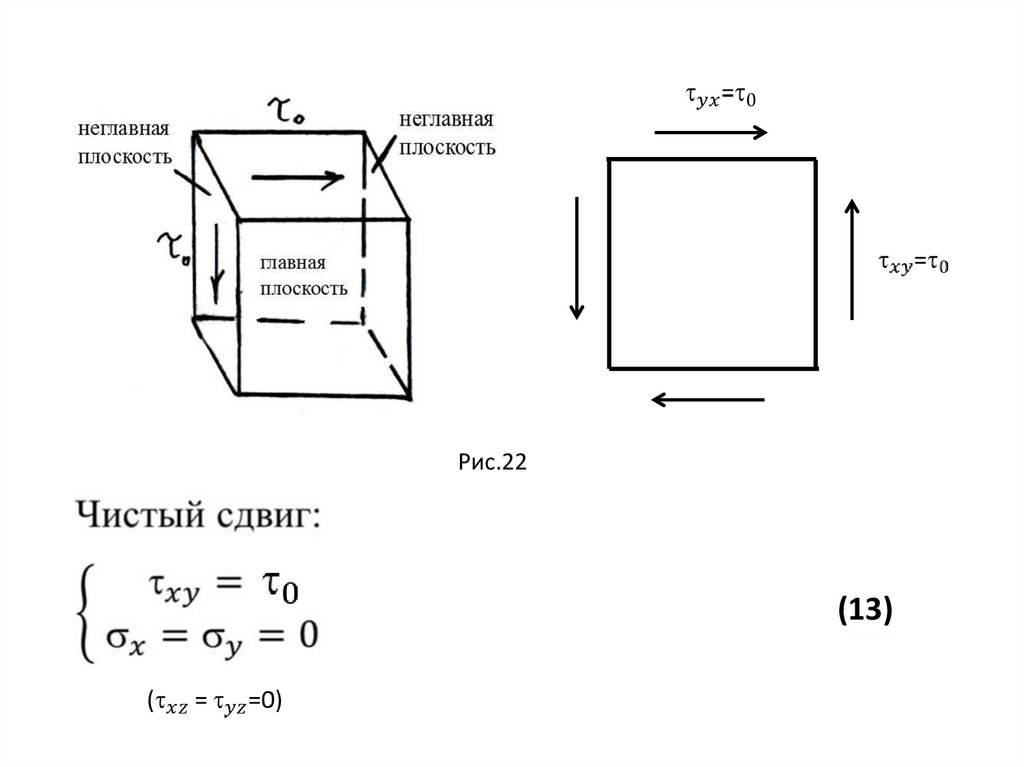
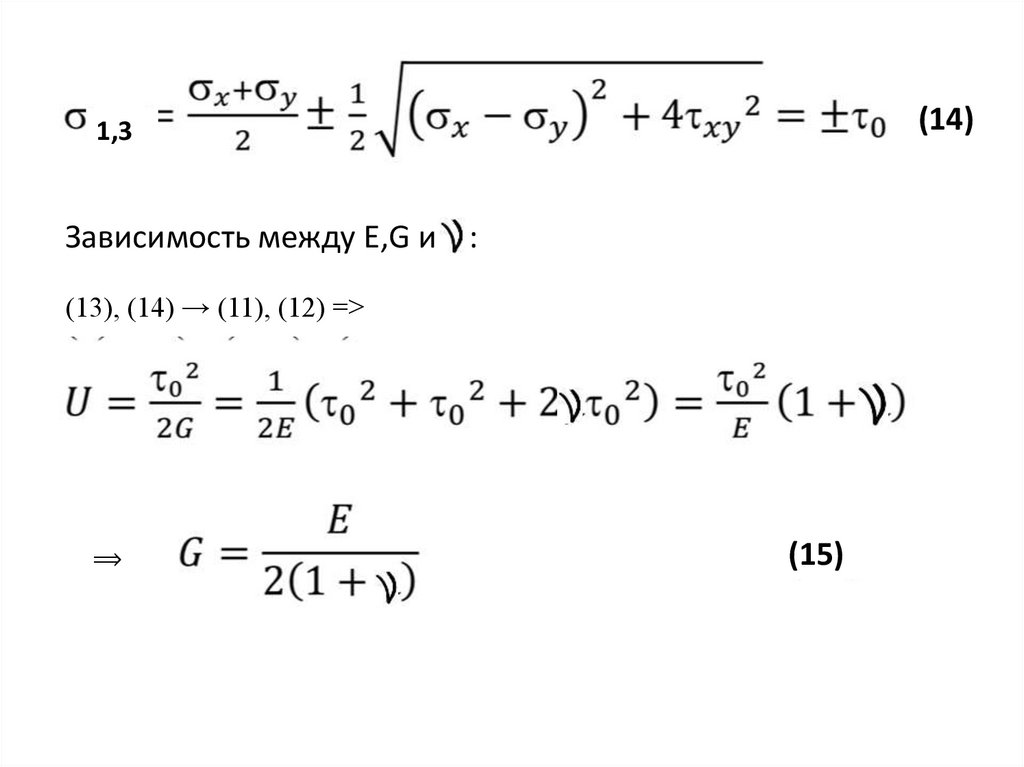






 Механика
Механика








