Похожие презентации:
Простейшие математические операции в КГ. Преобразования на плоскости
1.
Простейшиематематические
операции в КГ.
Преобразования на
плоскости
2.
Исторический экскурс3 сентября декабря – день комп. графики (3December)
3.
Исторический экскурс1950-е годы: от текстовых изображений к графической консоли
4.
1950-е годы1950, Бенджамин Лапоски, рисунки на осциллографе
5.
1950-е годы1952, Александр Дуглас, игра ОХО для компьютера EDSAC
6.
1950-е годы1955, IBM???, световое перо
7.
1950-е годы1957, Расселл Кёрш, барабанный сканер для компьютера SEAC,
первая в мире цифровая фотография
8.
1950-е годы1958, MIT, Lincoln TX-2, графическая консоль
9.
1950-е годы1958, Джон Уитни, предиктор Керрисона, заставка к фильму
Хичкока «Головокружение»
10.
1960-е годы: от "Альбома" кмультипликации
1960, Уильям Феттер, Boeing Aircraft, термин «компьютерная
графика»
11.
1960-е годы1962, Стив Рассел, Spacewar! для компьютера DEC PDP-1
12.
1960-е годы1963, Айван Сазерленд, Sketchpad для TX-2
13.
1960-е годы1963, Кен Ноултон, BeFlix – первый язык КГ
1965-1971, Стэн Вандербик, Poem Field
1967, университет Юты, НИИ КГ
1968, Evans&Sutherland
Эдвин Кэтмелл, Disney Pixar
Джон Уорнок, Adobe Systems, PostScript
Джеймс Кларк, Silicon Graphics, Netscape
1968, Николай Константинов, «Кошечка»
14.
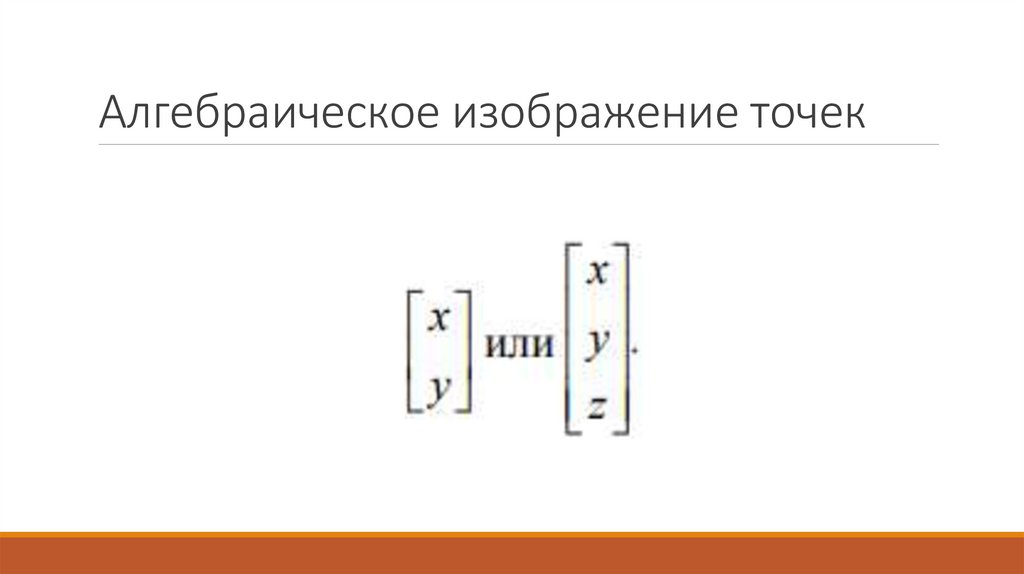
Алгебраическое изображение точек15.
Матричные операции. Определения.Матрица
Порядок матрицы
Главная диагональ
Нулевая матрица
Единичная матрица
16.
Сложение и вычитание матрицcij aij bij , i 1..n; j 1..m
17.
Умножение матрицA[k * m1], B[m2 * n], m1=m2 → A * B = C[k * n]
m
cij aik bkj
k 1
A B B A
18.
Определитель квадратной матрицыn
A 1 aij Aij
i j
j 1
Aij – алгебраическое дополнение матрицы A (матрица (n-1)*(n-1),
получаемая путем вычеркивания из матрицы А элементов i-ой
строки и элементов j-ого столбца)
19.
Определитель квадратной матрицыa11
A
a21
a11
A a 21
a 31
a12
a 22
a 32
a13
a 23
a 33
a12
,
a22
A a11a22 a21a12
A a11 a22 a33 a32 a23 a12 a21a33 a31a23
a13 a21a32 a31a22
20.
Обращение квадратной матрицы1
АТ = В → T A
B , А-1 — обратная к А
A11
1 A21
1
A
A
An1
A12
A22
An 2
A1n
A2 n
T
Ann
T – операция транспонирования(строки – в столбцы, столбцы – в
строки)
21.
Обобщение сути задач КГИнтерпретация матричного умножения как геометрического
оператора является основой математических преобразований,
используемых в машинной графике.
x
a b
y
ax cy
c d
bx dy x
*
y
*
22.
Преобразование точекx
1 0
y
x
0 1
y x
x
a 0
y
ax
0 1
y x
a>1 – увеличение масштаба,
0<a<1 – уменьшение масштаба,
а<0 – отображение по оси у
*
y
*
*
y
*
23.
Преобразование точек24.
Преобразование точек25.
Преобразование прямых линий26.
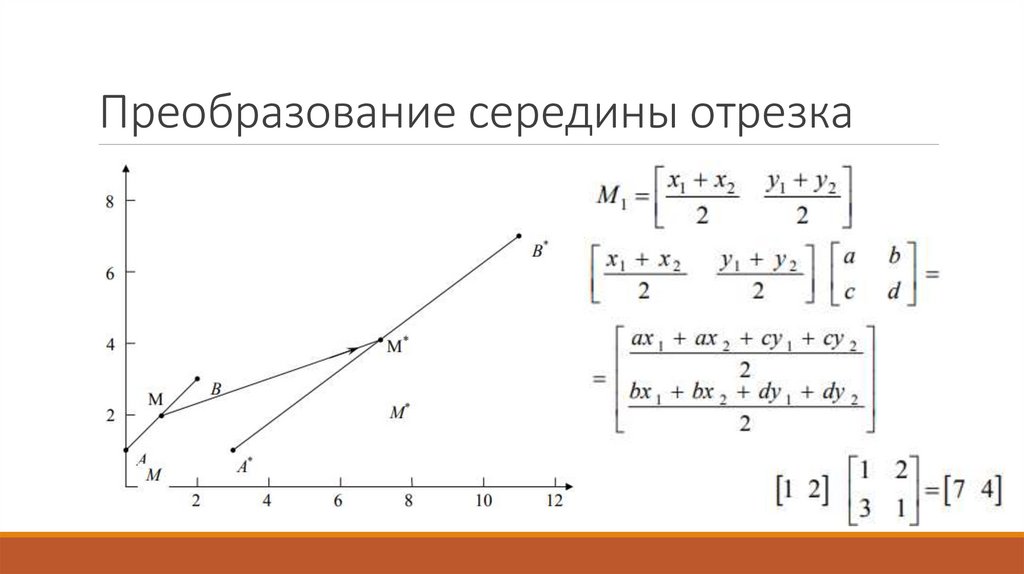
Преобразование середины отрезка27.
Преобразование параллельных линий28.
Преобразование пересекающихсялиний
29.
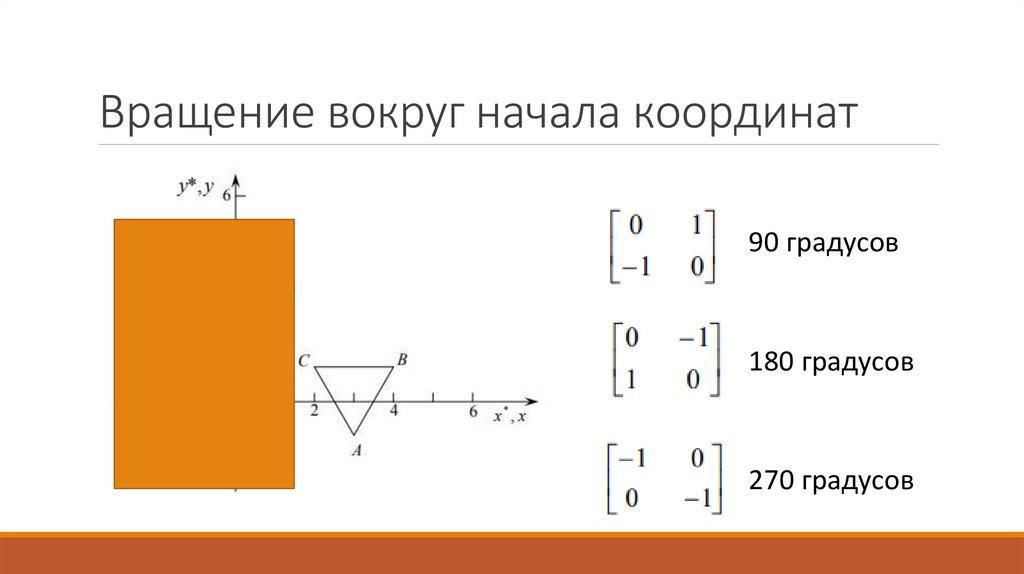
Вращение вокруг начала координат90 градусов
180 градусов
270 градусов
30.
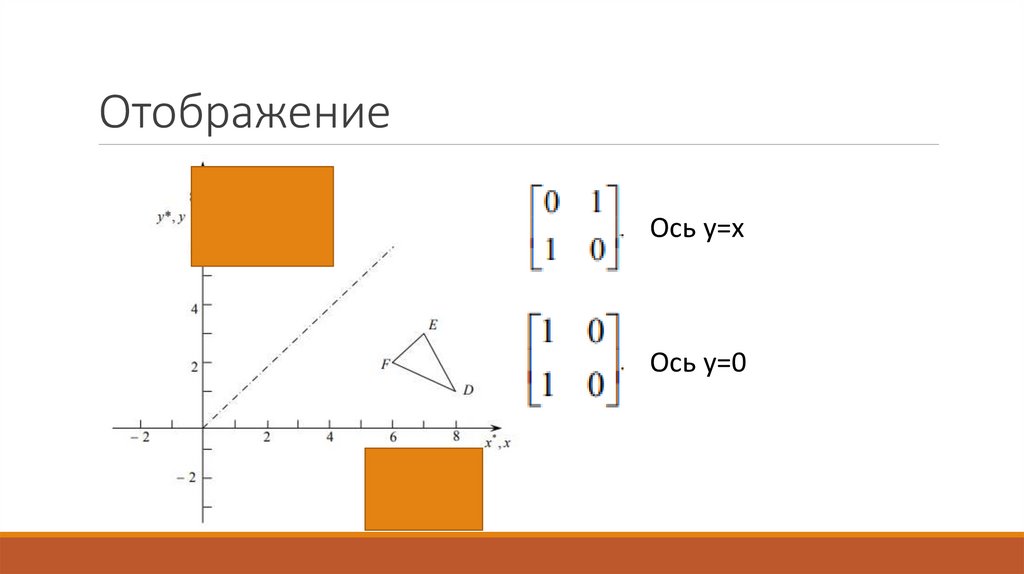
ОтображениеОсь y=x
Ось y=0
31.
Изменение масштабаИзменение масштаба
определяется значением двух
членов основной диагонали
матрицы.
a=d – масштабирование
a<>d – масштабирование с
искажением
32.
Произвольная матрица вращения33.
Однородные координаты и двумерноесмещение
x
1 0 0
y 1 0 1 0 x m
m n 1
y n 1 x
*
y
*
1
x
x ,
h
*
y
y
h
*
Представление n-мерного вектора
(n+1)-мерным называется
однородным координатным воспроизведением; координаты x, y, h однородными координатами.
34.
Однородные координаты и двумерноесмещение
Все преобразования матрицей 2 2 (вращение, отображение,
покоординатное масштабирование, смещение) реализуются в
однородных координатах с помощью матрицы:
a b
c d
0 0
0
0
x
y
1 x h ax cy, y h bx dy
a b 0
x y 1 c d 0 ax cy bx dy 1 x
0 0 1
*
*
y
h
35.
Общий вид матрицы преобразования3х3
a b
c d
m n
p
q
s
a, b, c, d – масштабирование, сдвиг и
вращение
m, n – перенос(двумерное смещение)
p, q, s – ???
36.
Полное изменение масштабаx
x
*
1 0 0
y 1 0 1 0 x
0 0 s
y
y x / s
y / s
*
s
s>1 – уменьшение, s<1 – увеличение
Аналогично использованию двумерной матрицы
1 / s 0
0 1 / s
37.
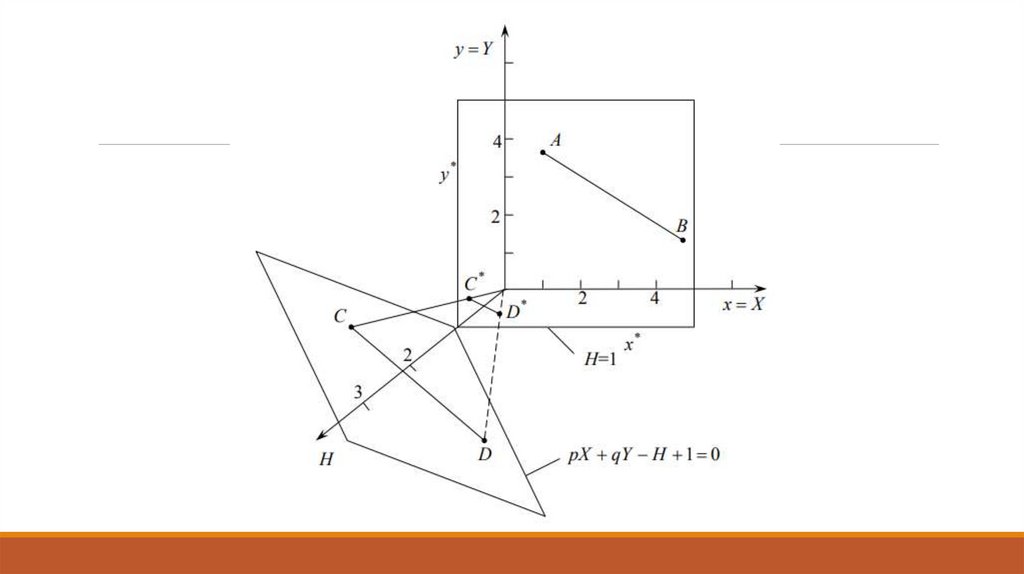
Получение проекций1 0 p
y 1 0 1 q x
0 0 1
x
y
px qy 1
Переменная H – уравнение плоскости в трёхмерном
пространстве
x
*
x
y
px qy 1
*
y
px qy 1

































 Математика
Математика








