Похожие презентации:
Телекоммуникационные системы и сети
1. Основные определения
Гришин ОПТССИнформация - совокупность сведений о каких-либо событиях, явлениях, фактах,
предметах и лицах независимо от формы их представления
Сообщение – форма представления информации для передачи ее от источника к
получателю
Данные - информация, представленная в виде, пригодном для обработки автоматическими
средствами при возможном участии человека
Сигнал – материальный носитель или физический процесс, отображающий сообщение
Связь – обмен информацией с помощью средств, функционирующих в соответствии с
согласованными правилами
Сеть связи - технологическая система, включающая в себя средства и линии связи и
предназначенная для электросвязи
Электросвязь – передача и прием сообщений с помощью сигналов электросвязи по
проводным, оптическим или беспроводным средам распространения
Система электросвязи – комплекс технических средств, обеспечивающих электросвязь
определенного типа
Средства связи - технические и программные средства, используемые для формирования,
приема, обработки, хранения, передачи, доставки сообщений электросвязи или почтовых
отправлений, а также иные технические и программные средства, используемые при
оказании услуг связи или обеспечении функционирования сетей связи
Линии связи - линии передачи, физические цепи и линейно-кабельные сооружения связи
2.
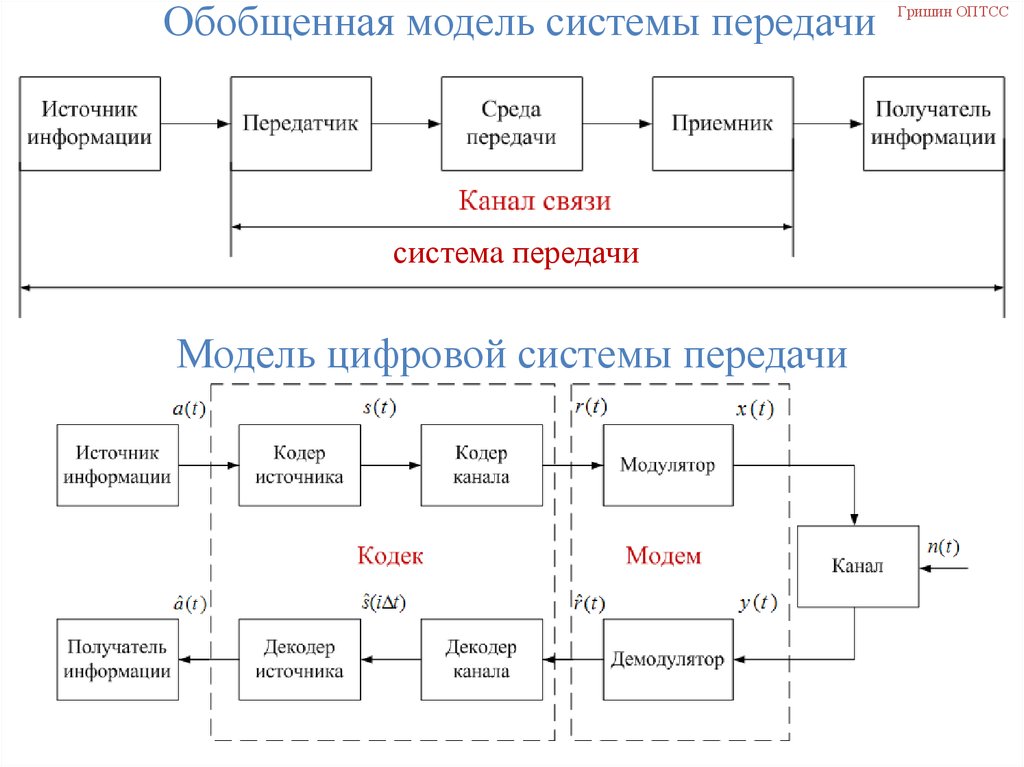
Обобщенная модель системы передачисистемa передачи
Модель цифровой системы передачи
Гришин ОПТСС
3.
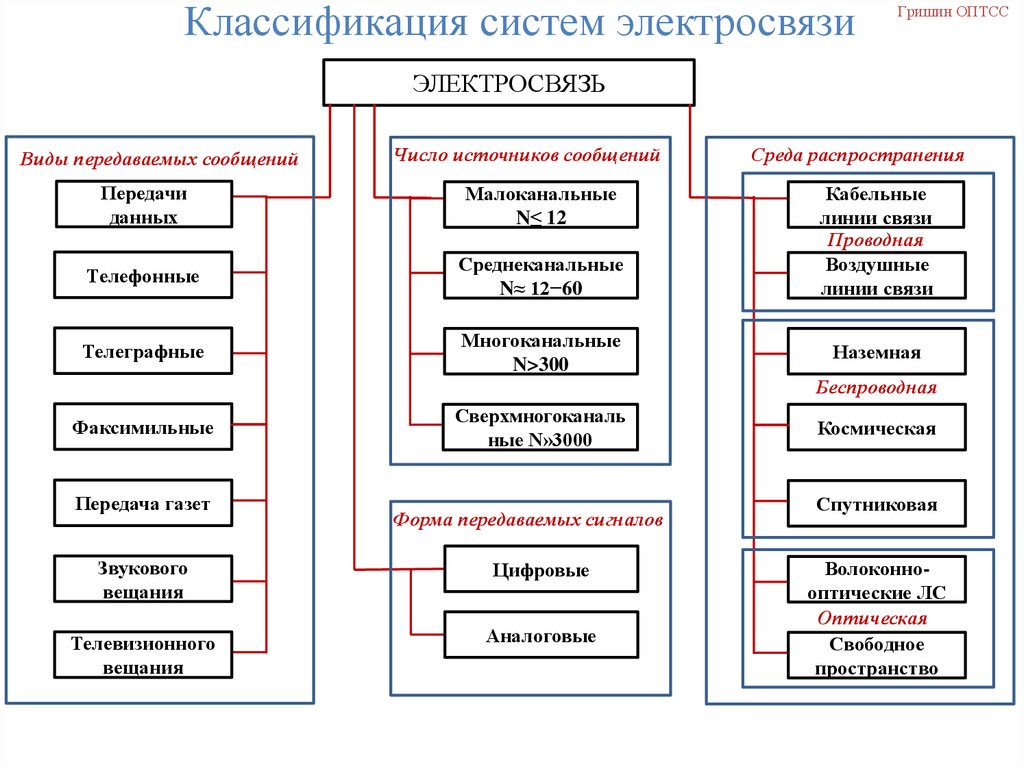
Классификация систем электросвязиГришин ОПТСС
ЭЛЕКТРОСВЯЗЬ
Виды передаваемых сообщений
Число источников сообщений
Передачи
данных
Малоканальные
N≤ 12
Телефонные
Среднеканальные
N≈ 12−60
Телеграфные
Многоканальные
N>300
Среда распространения
Кабельные
линии связи
Проводная
Воздушные
линии связи
Наземная
Беспроводная
Факсимильные
Передача газет
Сверхмногоканаль
ные N»3000
Форма передаваемых сигналов
Звукового
вещания
Цифровые
Телевизионного
вещания
Аналоговые
Космическая
Спутниковая
Волоконнооптические ЛС
Оптическая
Свободное
пространство
4.
МестныеЗоновые
Магистральные
Международные
Специального
назначения
Технологические
Выделенные
Общего
пользования
Коммутация
сообщений
По территориальному делению
Коммутация
пакетов
Фиксированной
связи
По типу коммутации
Коммутация
каналов
По типу абонентских терминалов
Подвижной
связи
Вторичные
Первичные
По способу организации каналов
Мультисервисные
Моносервисные
Количество служб электросвязи
Доступа
Транспортные
По функциональному признаку
По категориям
Классификация сетей связи
Гришин ОПТСС
СЕТИ СВЯЗИ
5.
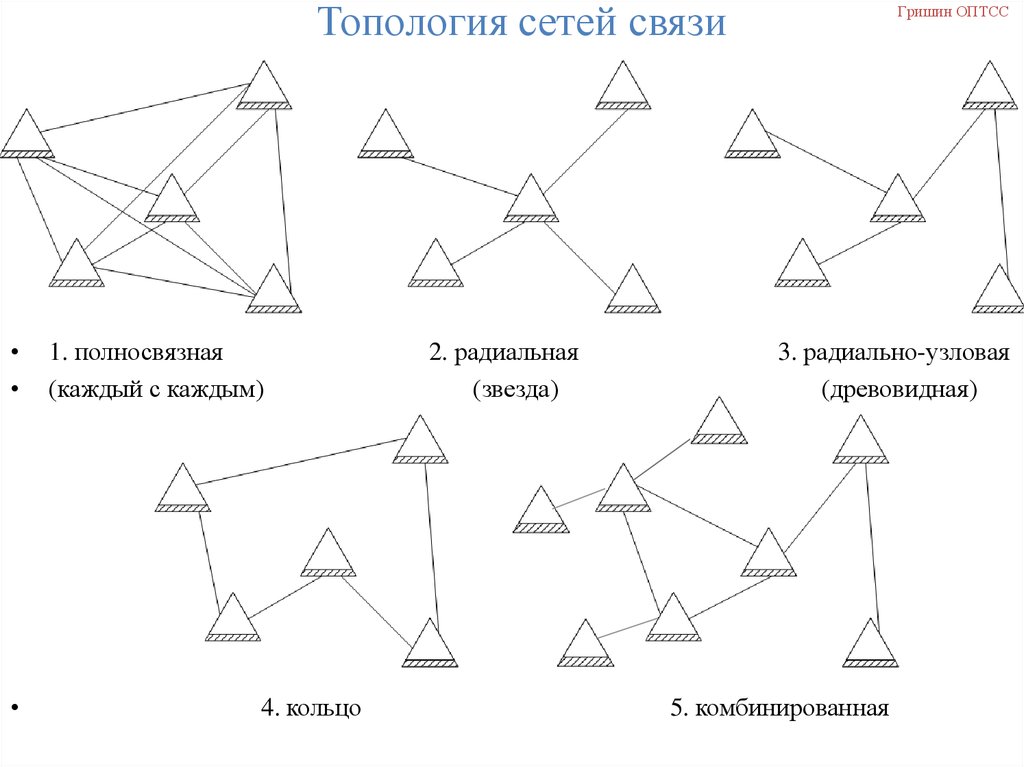
Топология сетей связи1. полносвязная
(каждый с каждым)
4. кольцо
2. радиальная
(звезда)
Гришин ОПТСС
3. радиально-узловая
(древовидная)
5. комбинированная
6.
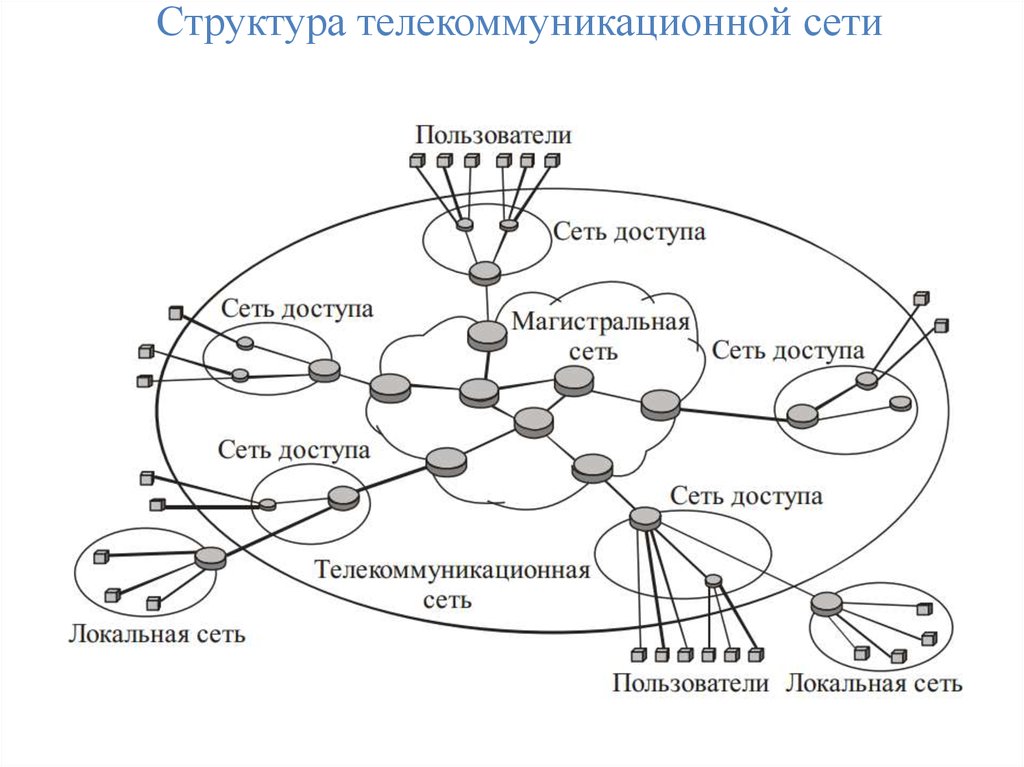
Структура телекоммуникационной сети7.
Структура первичной сетиГришин ОПТСС
8.
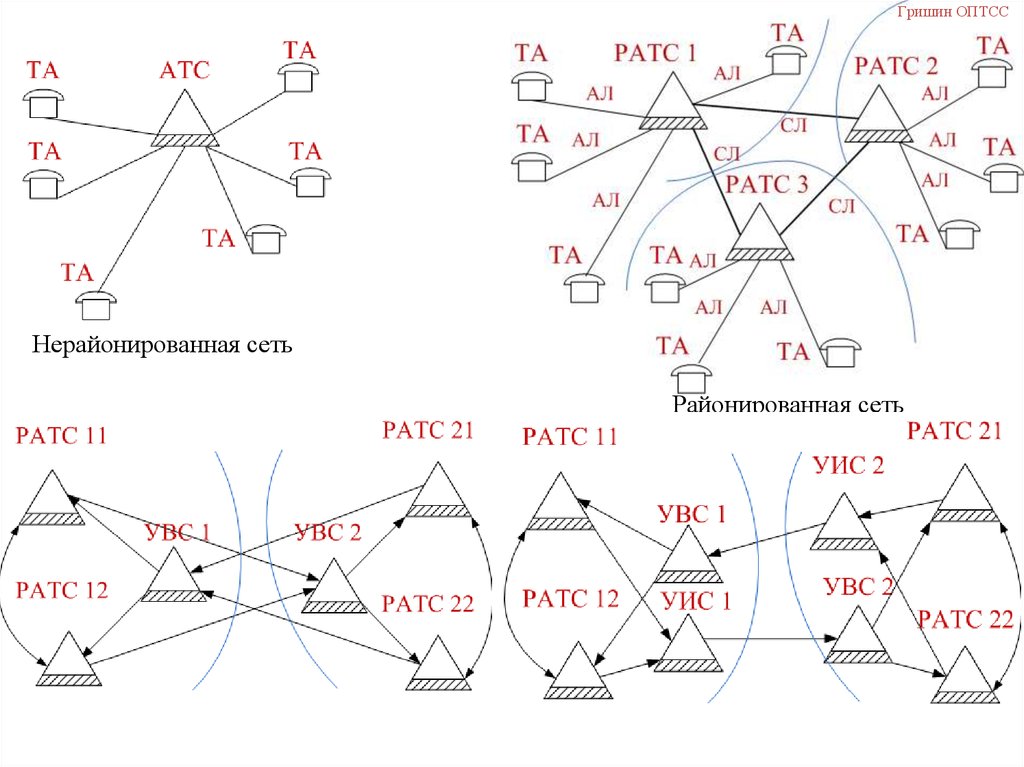
Гришин ОПТССНерайонированная сеть
Районированная сеть
9.
Уровни передаваемых сигналовГришин ОПТСС
Преимущества использования относительных величин:
1. Чувствительность слухового аппарата к воздействию звукового сигнала подчиняется логарифмическому
закону
2. Потери сигнала в линии подчиняются экспоненциальному закону
3. Порядок логарифмических величин оказывается меньшим, чем в случае использования абсолютных величин
4. Операции умножения и деления заменяются операциями сложения и вычитания
Уровень по мощности:
U2
Уровень по напряжению: pн 20 lg , дБ
U1
U
pн ln 2 , Нп
U1
Уровень по току:
I
pт 20 lg 2 , дБ
I1
I
pт ln 2 , Нп
I1
Абсолютный уровень: P1 P0 1 мВт , U1 U 0 0,775 В, I1 I 0 1,29 мА, R0 600 Ом p м , дБм pн , дБн pт , дБт
P
p м 10 lg 2 , дБ
P1
1 P
p м ln 2 , Нп
2 P1
pм pн pт
U 2 R 1
P2
U 22 R0
U
R
R
p м 10 lg 10 lg 2 10 lg 2 2 20 lg 2 10 lg 2 pн 10 lg 2
U 0 R0
P0
U 0 R2
U0
R0
R0
I 2 R
P2
I 22 R2
I
R
R
p м 10 lg 10 lg 2 10 lg 2 2 20 lg 2 10 lg 2 pт 10 lg 2
I 0 R0
P0
I 0 R0
I0
R0
R0
10.
Относительный уровень:
Гришин ОПТСС
U2
P
pом 10 lg 2 , дБмО pон 20 lg , дБнО
Uн
Pн
P P 1
P2
P2 P0
P
P
pом 10 lg 10 lg 10 lg 2 н 10 lg 2 10 lg 1 p2 p1 , дБмО
P0 P0
Pн
Pн P0
P0
P0
U U 1
U2
U2 U0
U
U
pон 20 lg 20 lg
20 lg 2 н 20 lg 2 20 lg 1 p2 p1 , дБнО
U0 U0
Uн
Uн U0
U0
U0
Pвых
P
Усиление м :S м a м 10 lg вых Коэффициент усиления м : K м
Pвх
Pвх
U
Затухание н:
Усиление н : S н 20 lg U вых
Коэффициент усиления н : K н вых
U
U вх
вх
P
P
Динамический диапазон: D 10 lg м акс , дБ
Пик –фактор : Q 10 lg макс , дБ
Pм ин
Pcp
P
Помехозащищенность сигнала: Aз 10 lg с , дБ
Pш
Затухание м :
P
а м 10 lg вх
Pвых
U
ан 20 lg вх
U вых
Диаграмма уровней:
11.
Основные характеристики сигналов электросвязиГришин ОПТСС
a0
s (t ) ak cos 2 kft bk sin 2 kft
2 k 1
2 T /2
2 T /2
s(t ) cos(2 kft )dt
a0
s(t )dt ak
T T / 2
T T / 2
S ( j ) s(t ) exp( j t )dt
1 2
s(t ) s (t )dt
T
2 T /2
bk
s(t ) sin( 2 kft )dt
T T / 2
1
S ( j ) exp( j t )d
s(t ) S ( j ) s(t )
2
U , t T / 2, T / 2
Пример: s(t )
0, t T / 2, T / 2
T /2
S ( j ) Re s (t ) exp( j t )dt Re U exp( j t )dt
T / 2
T /2
T /2
U
U
U
Re
exp( j t )
Re
cos( t ) j
sin( t )
j
j
T / 2
j
T / 2
T /2
U
U
sin( T )
jU
Re
cos( t ) sin( t )
sin( T ) UT
T
T / 2
12.
Иллюстрации к примеруГришин ОПТСС
13.
Теорема КотельниковаПусть
s(t ) S ( j ) S ( j 2 f ), f f min , f max
1 max
s(t )
S ( j ) exp( j t )dt
2 max
1 max
s(i t )
S ( j ) exp( j i t )d
2 max
1 max
s i t
S ( j ) ai exp( j i t ) ai
S
(
j
)
exp(
j
i
t
)
d
4 f max max
2 f max
i
1
S ( j )
s(i t ) exp( j i t )
2 f max i
max
1 1
s (t )
s (i t ) exp j t i t d
2 2 f max i
max
s (i t )
i
i
s (i t )
exp j 2 f max t i t exp j 2 f max t i t
2 f max 2 j t i t
sin 2 f max t i t
2 f max t i t
Гришин ОПТСС
14. Иллюстрации к примеру
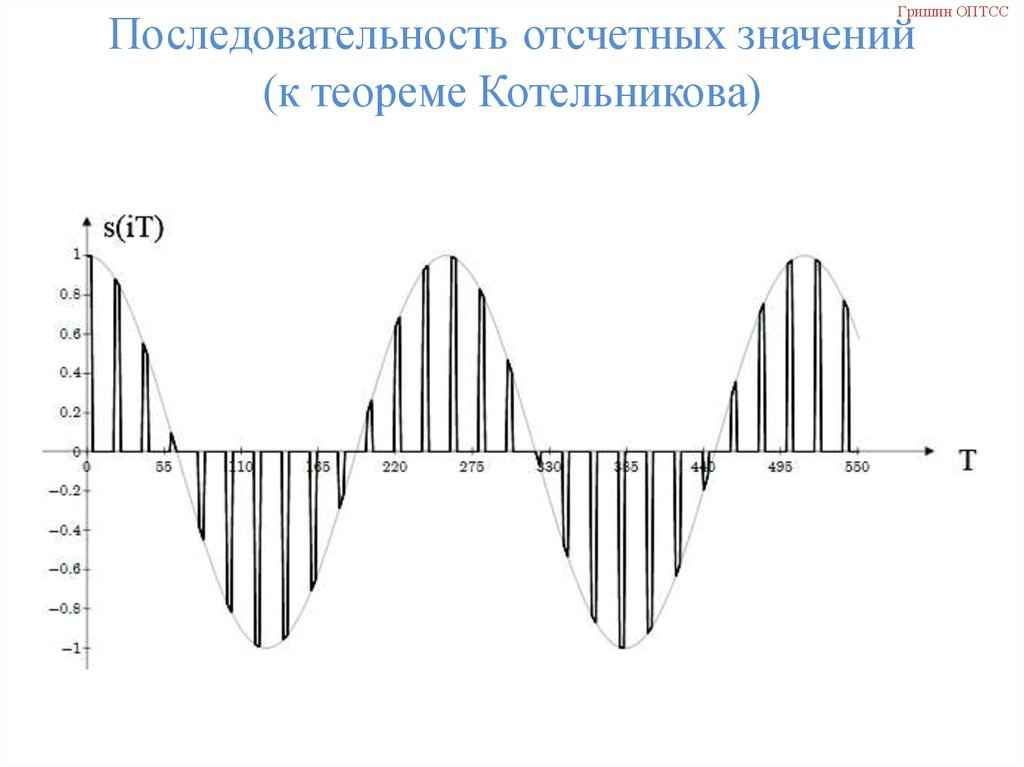
Гришин ОПТССПоследовательность отсчетных значений
(к теореме Котельникова)
е
15.
Гришин ОПТССИнформационные параметры сигналов электросвязи
Vc Tc f c D Объем сигнала
2Tc f c
База сигнала
1
узкополосный сигнал
1
широкополосный сигнал
N сообщ m n Общее число различных сообщений, m – объем алфавита A
I log 2 Nсообщ n log 2 m
p
1
I1 log 2 p
m
a1
A
p1
Количество информации (формула Хартли)
Количество информации на один символ
am
I i log 2 p(ai )
pm
m
H ( A) p(ai ) log 2 p(ai ) Среднее количество информации (энтропия ). Ф-ла Шеннона
i 1
m
H max ( A) p log 2 p
i 1
m
i pi p
m
1
m
mp log 2 p m
H max ( A' A) p ai p a 'j ai log 2 p a 'j ai
i 1
H ' H / t
j 1
Производительность источника
1
1
log 2 log 2 m
m
m
Условная энтропия
16. Последовательность отсчетных значений (к теореме Котельникова)
Гришин ОПТССВероятностные характеристики сигналов
Математическое ожидание:
m( s) E s(t ) sw( s, t )ds
Средний квадрат случайного процесса:
CK ( s) E s 2 (t ) s 2 w( s, t )ds
CK ( s)
Pcp ( s)
R
CK ( s)
Эффективное напряжение случайного процесса: U эф ( s)
R
2
Дисперсия: D( s ) E s (t ) m( s ) s (t ) m( s ) w( s, t )ds
Средняя мощность случайного процесса:
Корреляционная функция:
ks (t1 , t2 )
s(t1 )s(t2 )w(s1, s2 , t1, t2 )ds1ds2
Кросскорреляционная функция:
Эргодический процесс:
ksr (t1 , t2 )
s(t1 )r (t2 )w(s, r , t1, t2 )dsdr
1
s(t )dt
T T
sw(s, t )ds lim
1
ks (t1 , t2 ) lim s(t1 ) s(t2 )dt
T T
17. Информационные параметры сигналов электросвязи
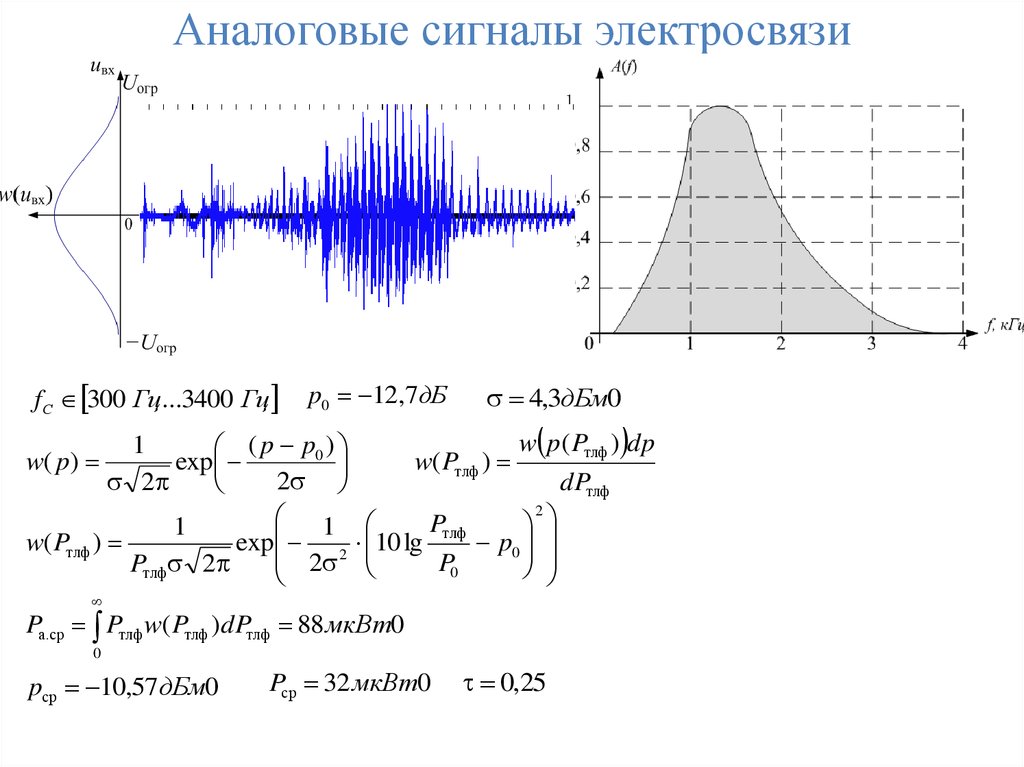
Аналоговые сигналы электросвязиfС 300 Гц...3400 Гц
p0 12,7дБ
4,3дБм0
w p( Pтлф ) dp
1
( p p0 )
exp
w( Pтлф )
2
dPтлф
2
2
1
P
1
тлф
w( Pтлф )
exp 2 10 lg
p0
2
P0
Pтлф 2
w( p)
Pа.ср Pтлф w( Pтлф )dPтлф 88 мкВт0
0
pср 10,57дБм0
Pср 32 мкВт0
0,25
18.
Одномерные цифровые сигналы электросвязиx(t )
xi g (t i t )
i
1
B
2 f , Бод
t
W m B 2 f log 2 M , бит / c
P
Wmax C f log 2 1 c , бит / c
Pш
S ( f ) x(t ) exp( j 2 ft )dt xi g (t i t ) exp( j 2 ft )dt
i
S ( f , i t )
g ( ) exp( j 2 f ) x exp( j 2 ft )d G ( f ) xi exp( j 2 ft )
i
i
M
w( x) pi x xi m( x)
i 1
i
M
pi xi
xw( x)dx
i 1
M
CK ( x) x w( x)dx pi xi2
2
i 1
19. Аналоговые сигналы электросвязи
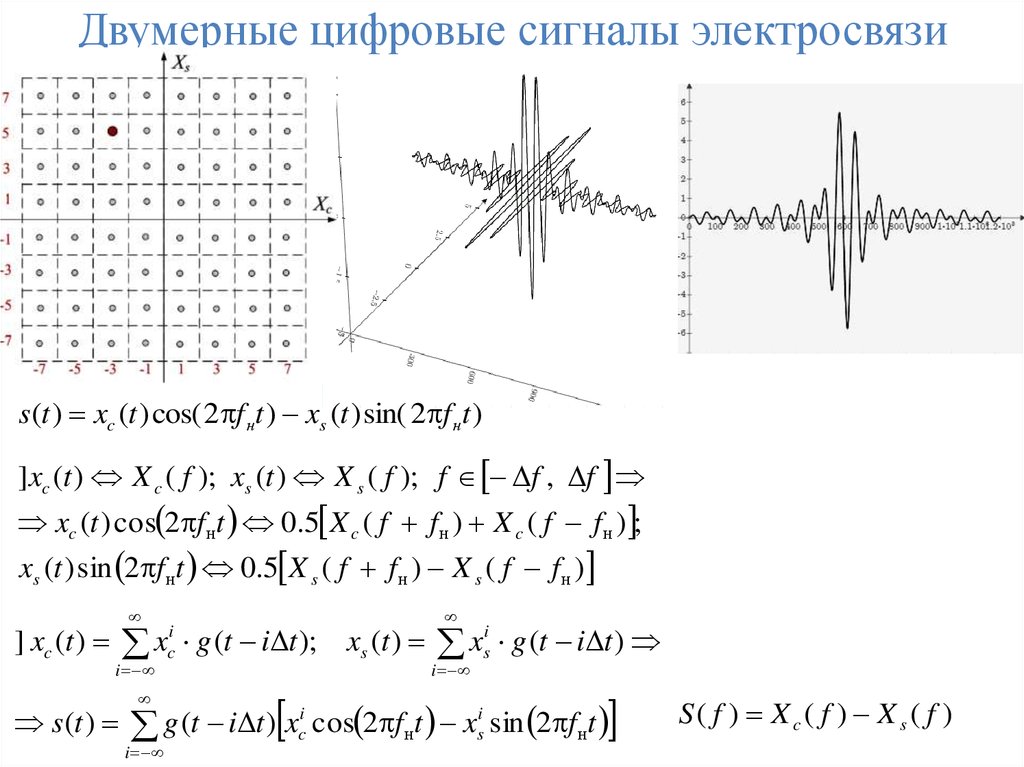
Двумерные цифровые сигналы электросвязиs(t ) xc (t ) cos( 2 f нt ) xs (t ) sin( 2 f нt )
]xc (t ) X c ( f ); xs (t ) X s ( f ); f f , f
xc (t ) cos 2 f нt 0.5 X c ( f f н ) X c ( f f н ) ;
xs (t ) sin 2 f нt 0.5 X s ( f f н ) X s ( f f н )
] xc (t )
x g (t i t ); xs (t )
i
s(t )
i
c
i
x
s g (t i t )
i
g (t i t ) xci cos 2 fнt xsi sin 2 fнt
i
S( f ) Xc( f ) Xs ( f )
20.
f 2 d 2 fШирина спектра двумерного сигнала
B2 d f 2 d , Бод символ / с
W2 d f 2 d log M c log M s , бит/c
w( xc , xs ) pci psi xc xci , xs xsj
Mc M s
i 1 j 1
m( xc , xs ) xc w( xc )dxc
Ms
Mc
pci xci psj xsj
xs w( xs )dxs
j 1
i 1
Mc
Ms
2
2
2
2
CK ( xc xs ) xc w( xc )dxc xs w( xs )dxs pci xci psj xsj
j 1
i 1
Двумерный цифровой сигнал на входе и выходе канала
21.
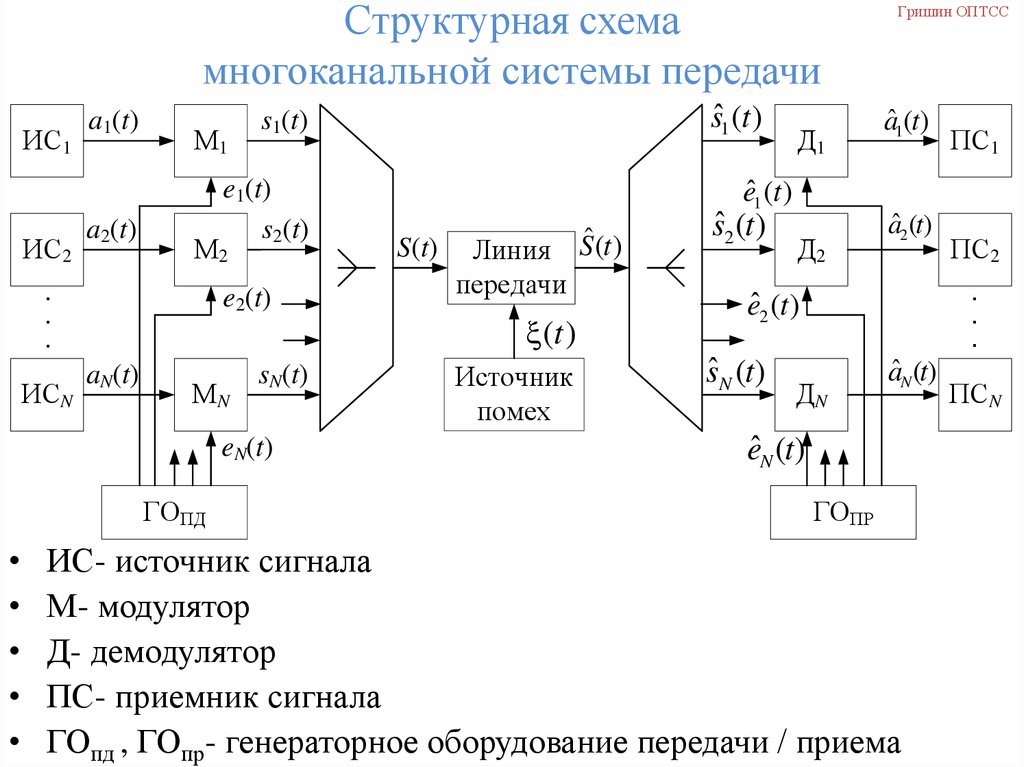
Структурная схемамногоканальной системы передачи
ИС2
a2(t)
М1
e1(t)
s2(t)
М2
. . .
e2(t)
ИСN
aN(t)
МN
sN(t)
eN(t)
ГОПД
sˆ1 (t )
s1(t)
Д1
eˆ1 (t )
S(t) Линия Sˆ (t )
передачи
(t )
Источник
помех
sˆ2 (t)
Д2
aˆ1(t)
aˆ2 (t)
eˆ2 (t )
sˆN (t)
ПС1
ПС2
. . .
ИС1
a1(t)
Гришин ОПТСС
ДN
aˆN (t)
eˆN (t)
ГОПР
ИС- источник сигнала
М- модулятор
Д- демодулятор
ПС- приемник сигнала
ГОпд , ГОпр- генераторное оборудование передачи / приема
ПСN
22.
Пояснения к структурной схеме МСПsn (t ) M n an (t )
N
N
линейное преобразование : M n n an (t ) n M n {an (t )}
n 1
n 1
N
N
n 1
n 1
S (t ) U sn (t ) U M n an (t ) sn (t ) M n an (t )
Sˆ (t ) L[ S (t ), (t )]
sˆn (t ) U 1 Sˆ (t )
aˆn (t ) M n 1 sˆn (t ) M n 1 U 1 L U M n an (t )
Гришин ОПТСС
23. Структурная схема многоканальной системы передачи
Линейное разделение сигналовГришин ОПТСС
S (i t ) e1a1 (i t ) e2 a2 (i t ) ... en an (i t )
S1 e11a1 e12a2 ... e1N aN
S 2 e21a1 e22a2 ... e2 N aN
...
...
...
...
...
...
S N eN 1a1 eN 2 a2 ... eNN aN
1
a1
e11
e
21
eN 1
2
a2
N
... aN
e1N
S1
S
e2 N
1 2
eNN
S N
e1N
e11
e
e2 N
... N 21
eNN
eN 1
S1
S2
SN
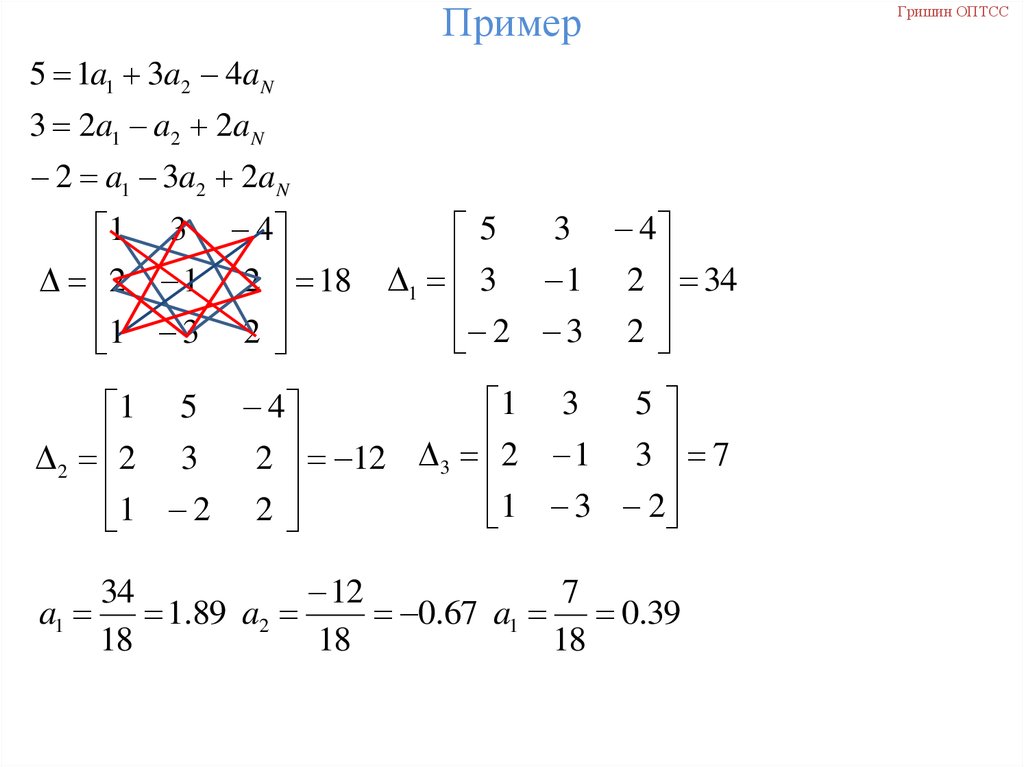
24. Пояснения к структурной схеме МСП
Пример5 1a1 3a2 4a N
3 2a1 a2 2a N
2 a1 3a2 2a N
1 3 4
2 1 2 18
1 3 2
3 4
5
1 3 1 2 34
2 3 2
5
1 3
1 5 4
2 2 3
2 12 3 2 1 3 7
1 3 2
1 2 2
34
12
7
a1
1.89 a2
0.67 a1 0.39
18
18
18
Гришин ОПТСС
25.
Гришин ОПТССУсловие линейного разделения сигналов
e11
e12
e1N 0
e
e
e 0
21
22
2N
a1
a2
aN
a1 a2 aN 0
eN 1
eN 2
eNN 0
a1e1 a2e2 aN e N 0
11
21
Г
N1
12
22
N2
1 N
2N
NN
N
ij e e j eine jn
T
i
Г 0 e1 , e2 , , e N Линейно независимы
Г 0 e1 , e2 , , e N Линейно зависимы
n 1
26. Пример
Гришин ОПТСС0 1a1 3a2 4a N
1
3
4
0 2a1 a2 2a N e1 2 e 2 1 e3 2
1
3
2
0 1a1 3a2 2a N
11 e1T e1 1 1 2 2 1 1 6
12 e1T e2 1 3 2 ( 1) 1 ( 3) 2
13 e1T e3 2
21 eT2 e1 2
31 eT3 e1 2
32 eT3 e2 20
2
2
6
Г 2 19 20 324
2 20 24
22 eT2 e2 19
23 eT2 e3 20
33 eT3 e3 24
=> Сигналы линейно независимы
27.
Гришин ОПТСС0 1a1 3a2 2a N
1
3
2
0 2a1 a2 4a N e1 2 e 2 1 e3 4
1
3
2
0 1a1 3a2 2a N
2 12
6
Г 2 19
4 0
12 4
24
e3 2e1
=> Сигналы линейно зависимы
28. Пример
Гришин ОПТССМаксимальное количество линейно разделимых
сигналов в N-мерном линейном пространстве
a1e1 a2e2 aN e N 0
a1e1 a2e 2 aN e N e N 1 0
EA e N 1 0
e N 1 EA
1
A E e N 1
e11 e12
e
e22
21
E
eN 1 eN 2
e1N
a1
a
e2 N
A 2
eNN
aN
29.
Формирование группового сигналаГришин ОПТСС
N
S a1e1 a2e2 aN e N s1 s 2 ... s N s n
n 1
S EA
1
1
A E S E EA
11
21
1
T
E E E E
N1
12
22
N2
1N 1 0 0
0 1 0
2N
I
NN 0 0 1
1, i j
ij e e j
0, i j
T
i
e S a e e a e e a e e a2
T
2
T
1 2 1
T
2 2 2
T
N 2 N
30.
Гришин ОПТССРазделение линейно-независимых сигналов
b1 c11e1 c12e 2 c1N e N
b 2 c21e1 c22e 2 c2 N e N
b N cN 1e1 cN 2e 2 cNN e N
1, i j
b ej
0, i j
T
i
i, j 1...N
31.
22
e1 e2
1
2
Пример
b1 c11e1 c12e2
b2 c21e1 c22e2
b e 1 b e 0 b e 0 b e 1
b1T e1 c11e1T e1 c12eT2 e1 c115 c12 6 1
T
T
T
b1 e 2 c11e1 e 2 c12e 2 e 2 c116 c12 8 0
T
1 1
T
1 2
T
2 1
T
2 2
bT2 e1 c21e1T e1 c22eT2 e1 c215 c22 6 0
T
T
T
b 2 e 2 c22e1 e 2 c22e 2 e 2 c216 c22 8 1
c11 0.125
c21 1.5
c12 0.271
c22 1.25
Гришин ОПТСС
32.
Гришин ОПТССРазделение сигналов с конечной энергией
( i 1) t
2
n
i t
e
( i 1) t
i t
(t )dt , n 1...N
1, i j
ei (t )e j (t )dt
i, j 1..N
0, i j
N
S (t ) a1e1 (t ) a2e2 (t ) aN eN (t ) anen (t ) A E(t )
n 1
( i 1) t
A
S (t )E(t )dt
i t
an
( i 1) t
s(t )en (t )dt,
i t
n 1...N
T
33.
Гришин ОПТССРазделение сигналов с конечной мощностью
const , i j
g (t , )ei ( )e j ( )d 0, i j i, j 1..N
sin( ) g ( ) G( ) G0 , 0
g ( ) 2G0 f
0,
N
S (t ) an (t )en (t ) A (t )E(t )
T
n 1
A(t ) E( ) S ( ) g (t )d
an (t ) en ( ) S ( ) g (t )d
34.
Гришин ОПТССАналоговые системы передачи
с частотным разделением каналов
A1 ( f )
S1 ( f )
f1
f
fн
fв f
AN ( f )
fн
S2 ( f )
f2
fN
f
f2+fн f2+fв
...
...
A2 ( f )
f
f1+fн f1+fв
SN ( f )
fв f
fN+fн fN+fв
f
S ( f )
...
f1+fн
fN+fв
f
35.
Структурная схема МСП с ЧРКПФ1
a1 (t )
s1(t )
ПФ1
sˆ1 (t )
ФНЧ1
ИС1
aˆ1 (t )
ПС1
ПФ2 s2 (t)
a2 (t )
ИС2
s (t)
Линия
передачи
e2 (t )
eˆ1 (t )
ПФ2 sˆ2 (t )
ФНЧ2 aˆ2 (t )
ПС2
eˆ2 (t )
ПФN sˆN (t )
ПФN sN (t )
aN (t )
sˆ (t)
...
e1 (t )
...
Гришин ОПТСС
ФНЧN aˆ N (t )
ИСN
ПСN
eˆN (t )
eN (t )
ГОпд
АМ-ОБП
ГОпр
36. Аналоговые системы передачи с частотным разделением каналов
Амплитудная модуляцияГришин ОПТСС
an (t ) = Ancos(2 f ct )
en (t ) = Encos(2 f nt )
An
sn (t ) = En 1 + cos(2 f ct ) cos(2 f nt ) = En (1 + man (t ) )cos(2 f nt )
En
En cos(2 f nt ) 0.5mEn cos 2 ( f n f c )t cos 2 ( f n f c )t
N
s (t ) sn (t )
n 1
Sn ( f )
En
mE n
2
fn fc
Виды амплитудной модуляции
mE n
2
fn
fn fc
Спектр модулированного сигнала
f
1.
2.
3.
4.
5.
АМ-ДБП-Н
АМ-ДБП
АМ-ОБП-Н
АМ-ОБП
АМ-ЧП
37. Структурная схема МСП с ЧРК
1an (t)
2
2
an* (t)
,
Универсальный квадратурный модулятор
3
scos,n (t )
en (t)
2
5
*
n
e (t )
4
6
ГО
7
sn (t )
an (t ) = Ancos(2 f ct )
an* (t ) = Ansin(2 fct )
ssin,n (t )
en (t ) = Encos(2 f nt )
en* (t ) = Ensin(2 f nt )
scos,n (t ) = An Encos(2 f ct )cos(2 f nt )
An En
cos 2 ( f n fc )t cos 2 ( f n fc )t
2
ssin,n (t ) = An Ensin(2 f ct )sin(2 f nt )
An En
cos 2 ( f n fc )t cos 2 ( f n fc )t
2
Гришин ОПТСС
38.
Системы передачи свременным разделением каналов
Tд
1
1
Fд 2 Fв
sin( 2 Fвt )
g (t )
2 Fвt
a(t ) a(iTд ) g (t iTд )
i
sin 2 Fв (t iTд )
a(iTд ) 2 F (t iT )
i
в
д
sn (t ) an (t )en (t ) an (t ) en (t kTд )
k
N
N
n 1
n 1
s (t ) sn (t ) an (t ) en (t kTд (n 1) )
k
Гришин ОПТСС
39. Универсальный квадратурный модулятор
Гришин ОПТСССтруктурная схема МСП с ВРК
s1(k t)
ВС1
ИС1
ФНЧ2
s2(k t)
ИС2
s (k t ) sˆ (k t )
Линия
передачи
ИСN
eN (k t )
sˆN (k t )
ФНЧN
...
CСпд
CСпр
ФИ
ГОпд
ГОпр
ЗГпд
ЗГпд
aˆ N (t )
ПСN
eˆN (t )
...
ФИ
ПС2
eˆ2 (t )
ВСN
sN(k t)
sˆ2 (k t )
aˆ2 (t )
ФНЧ2
...
...
ВС2
...
a N (t ) ФНЧN
...
e2 (k t )
ПС1
eˆ1 (t )
e1 (k t )
a2 (t )
sˆ1(k t)
aˆ1 (t )
ФНЧ1
...
a1 (t ) ФНЧ1
40. Системы передачи с временным разделением каналов
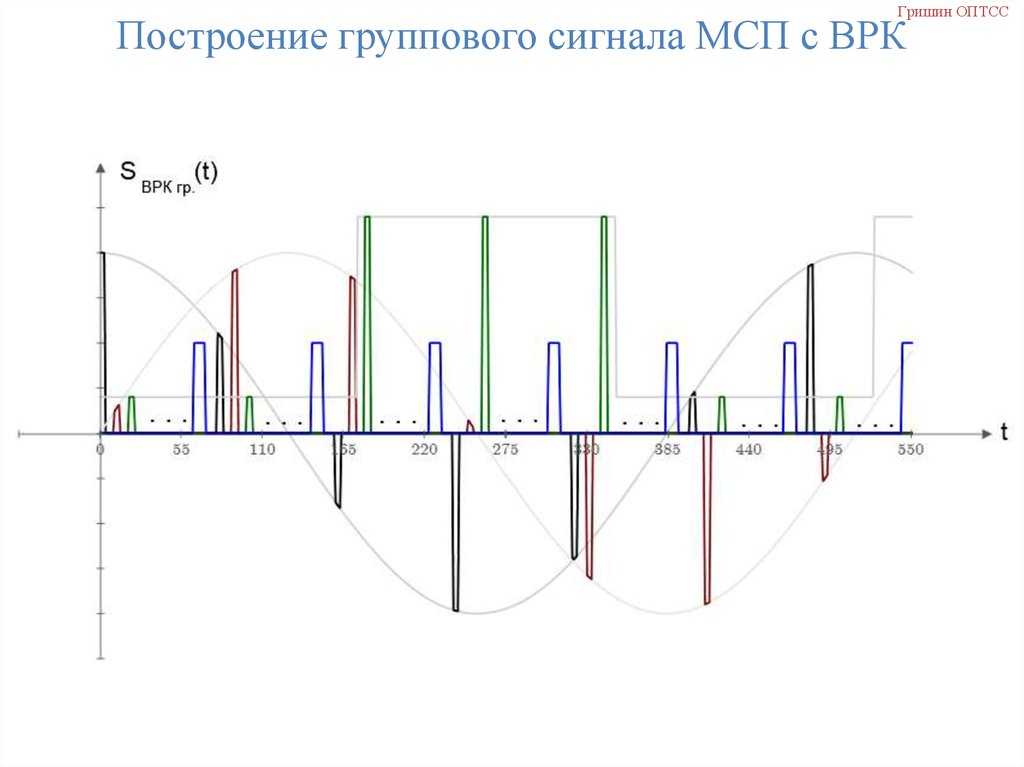
Гришин ОПТССПостроение группового сигнала МСП с ВРК
41.
Гришин ОПТССАмплитудно-импульсная модуляция 1-го рода
s(t), sАИМ-1(t)
s(t)
sАИМ-1(t)
e(t)
t
Tд
a(t ) = A0 A1cos(2 f ct ) A0 A1cos( t )
sАИМ 1 (t ) a(t )e(t ) a(t ) e0 (t kTд )
k
sАИМ 1 (t ) ( A0 A1 cos t ) e0 (t kTд )
k
42. Построение группового сигнала МСП с ВРК
22
4
cos n t
e
(
t
kT
)
e
(
t
)
dt
e
(
t
)
cos
n
tdt
0
T 0
д
0
д
д
T
k
n 1
0
д 0
д
e0 (t kTд ) f д E0 (0) 2 f д E0 (n д ) cosn дt
Tд
2
k
Гришин ОПТСС
Tд
n 1
s АИМ 1 (t ) A0 f д E0 (0) 2 E0 (n д ) cos n дt
n 1
A1 f д E0 (0) cos t E0 (n д ) cos(n д )t cos(n д )t
n 1
Спектр сигнала АИМ-1
k Ωд τ
sin
Uτ
2Uτ
2 S (kΩ Ω)
SАИМ 1 (Ω)
S (Ω )
д
Tд
Tд k 1 k Ω д τ
2
43.
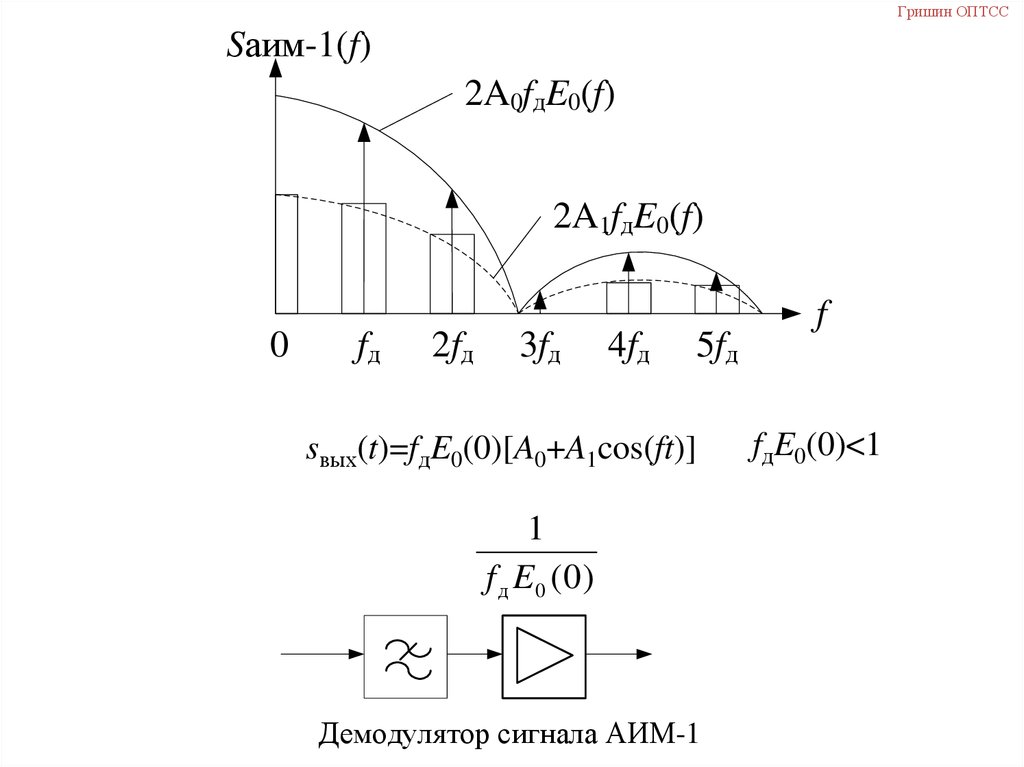
Гришин ОПТССSаим-1(f)
2A0fдE0(f)
2A1fдE0(f)
0
fд
2fд
3fд
4fд
5fд
sвых(t)=fдE0(0)[A0+A1cos(ft)]
1
f д E0 (0)
Демодулятор сигнала АИМ-1
f
fдE0(0)<1
44. Спектр сигнала АИМ-1
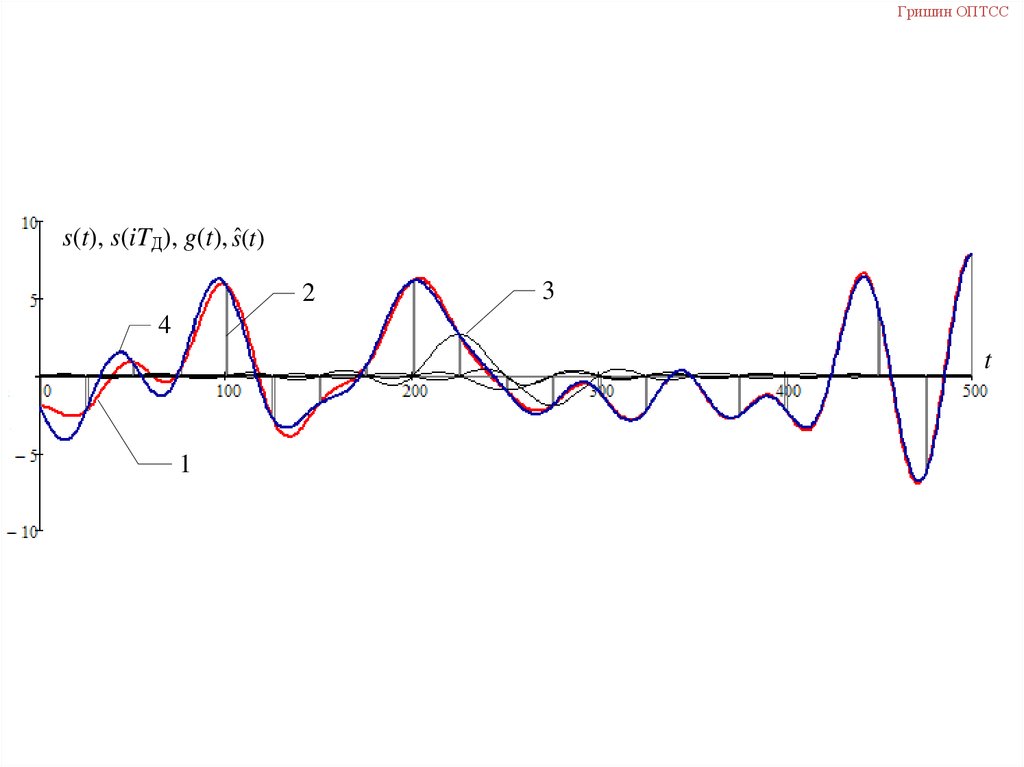
Гришин ОПТССs(t), s(iTД), g(t), sˆ(t )
2
3
4
t
1
45.
Пример46.
Гришин ОПТССАмплитудно-импульсная модуляция 2-го рода
s(t), sАИМ-2(t)
Кл1
s(t)
C
e1(t) e2(t)
sАИМ-2(t)
Кл2
t
Tд
sАИМ 2 (t ) a(kTд )e0 (t kTд )
k
s АИМ 2 (t ) A1 cos kTд e0 (t kTд )
k
1
i kTд i t
e0 (t kTд )
E
(
)
e
e d
0
2
47. Пример
cos kTд ei kTд
k
1 i kTд
i kTд
i kTд
e
e
e
k 2
Гришин ОПТСС
1 i ( ) kTд
i ( ) kTд
i ( ) kTд
i ( ) kTд
1 (e
e
e
e
)
2 k 1
1
1
cos( )kTд cos( )kTд .
2 k 1
2 k 1
2
1
cos zkx x n
z
2 k 1
z n
cos kTд e
i kTд
k
д
n
n
д
д
2 n
n
s АИМ 2 (t ) A1 f д E0 ( ) cos t E0 (k д ) cos(k д )t
k 1
E0 (k д ) cos(k д )t .
k 1
48. Амплитудно-импульсная модуляция 2-го рода
Гришин ОПТССs АИМ 2 (t ) A1 E0 ( )e
i t
fд
n
n
д
д d
2 n
n
fд
i ( n ) t
i ( n ) t
A1 E0 n д e д
E0 n д e д
.
2 n
s АИМ 2 (t ) A1 f д E0 ( ) cos t E0 (k д ) cos(k д )t
k 1
E0 (k д ) cos(k д )t .
k 1
E0 ( ) E0 ( )
eix e ix
cos x
2
49.
Гришин ОПТСССпектр сигнала АИМ-2
f τ
sin
Uτ
2
SАИМ 2 ( f )
S
(
f
)
2
S
(
k
f
f
)
д
Tд
fτ
k 1
2
Sаим-2(f)
2A0fдGи(f)
2A1fдGи(f)
0
fд
2fд
3fд
4fд
5fд
Демодулятор сигнала АИМ-2
1
Ω д E 0 (Ω )
Ф
К
f
50.
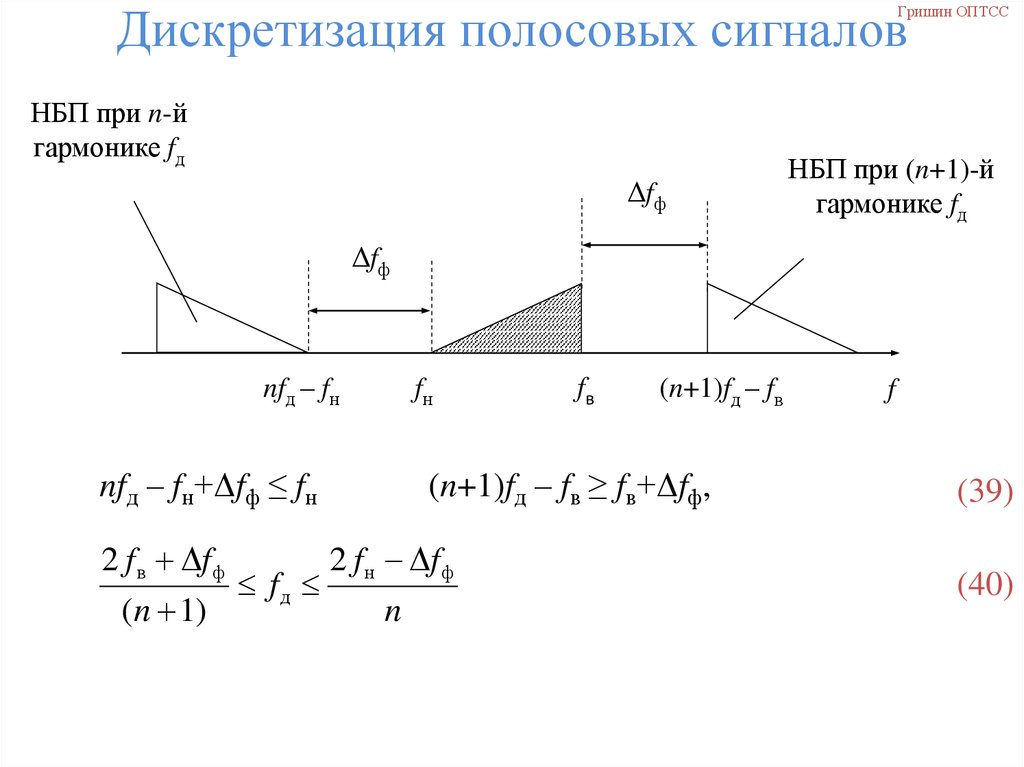
Дискретизация полосовых сигналовГришин ОПТСС
НБП при n-й
гармонике fд
Δfф
НБП при (n+1)-й
гармонике fд
Δfф
nfд – fн
fн
nfд – fн+Δfф ≤ fн
2 f в fф
(n 1)
fд
fв
(n+1)fд – fв
(n+1)fд – fв ≥ fв+Δfф,
2 f н fф
n
f
(39)
(40)
51. Спектр сигнала АИМ-2
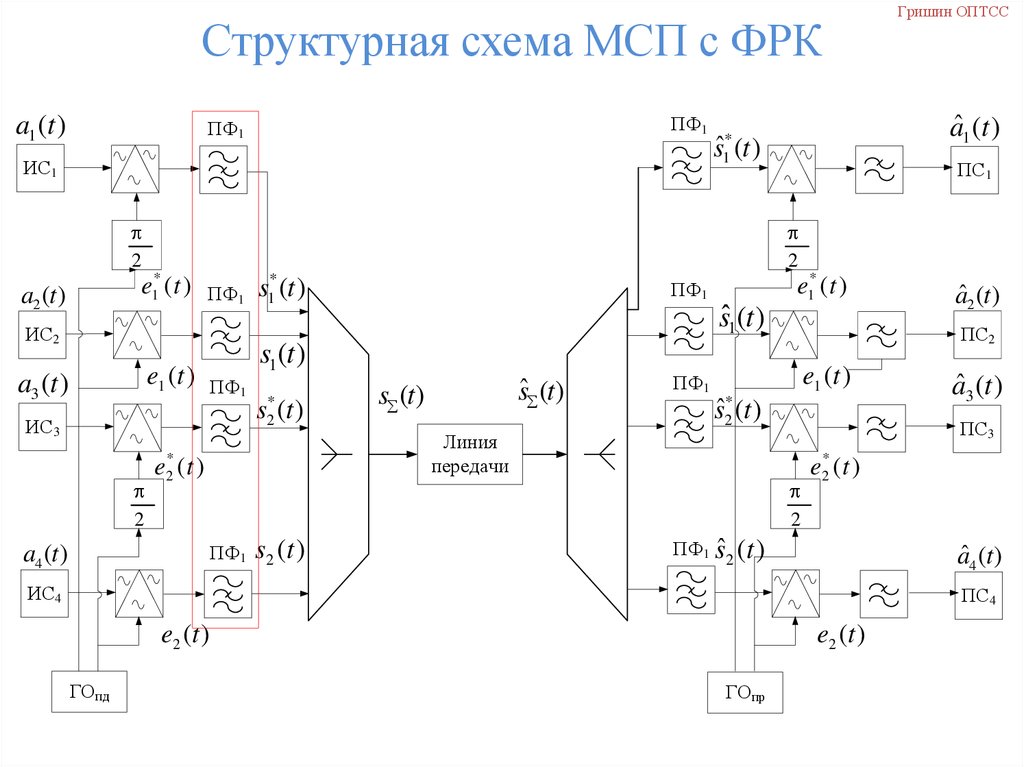
Гришин ОПТСССтруктурная схема МСП с ФРК
a1 (t )
ПФ1
ПФ1
ИС1
sˆ (t )
e1* ( t )
ПФ1
ИС2
e1 (t )
a3 (t )
ИС3
2
ПС1
2
2
a2 (t )
aˆ1 (t )
*
1
s1* (t )
ПФ1
s1(t )
ПФ1
ПФ2
*
2
s (t )
s (t)
e1 (t )
ПФ1
ПФ2 sˆ* (t )
ПФ2
2
2
ПФ1
s 2 (t )
aˆ2 (t )
ПС2
Линия
передачи
e2* ( t )
a4 (t )
sˆ (t)
sˆ1 (t )
e1* ( t )
aˆ3 (t )
ПС3
e2* ( t )
ПФ1 sˆ2 (t )
aˆ4 (t )
ИС4
ПС4
e2 (t )
e2 (t )
ГОпд
ГОпр
52. Дискретизация полосовых сигналов
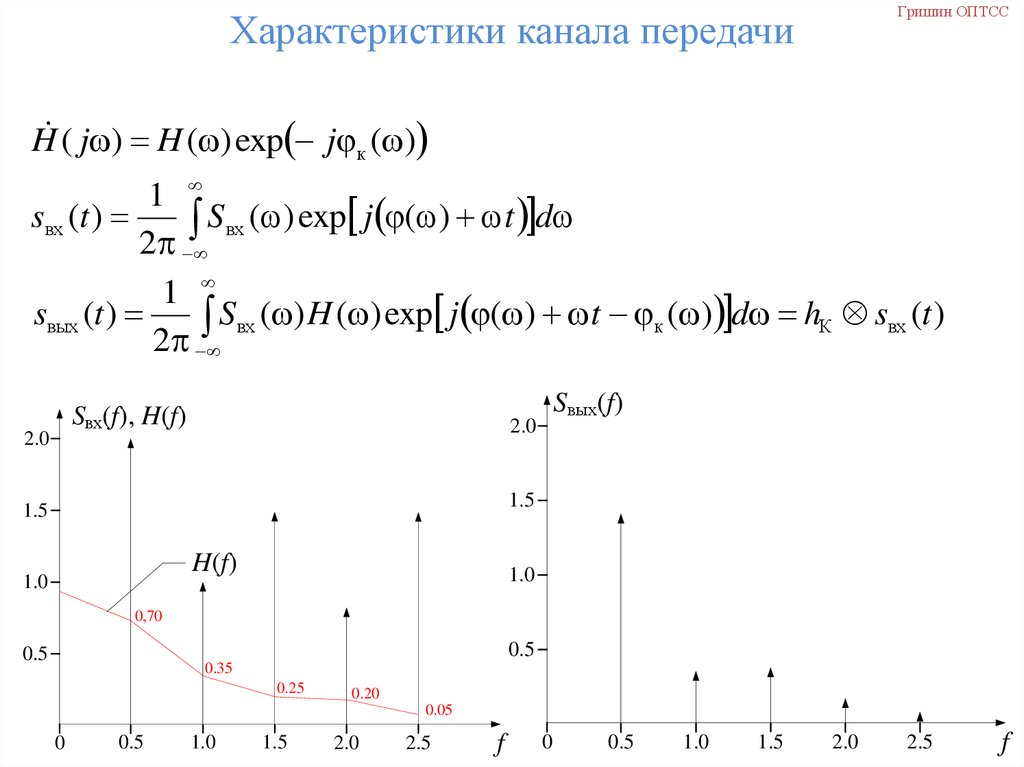
Гришин ОПТССХарактеристики канала передачи
H ( j ) H ( ) exp j к ( )
1
sвх (t )
Sвх ( ) exp j ( ) t d
2
1
sвых (t )
Sвх ( ) H ( ) exp j ( ) t к ( ) d hК sвх (t )
2
Sвх(f), H(f)
2.0
Sвых(f)
2.0
1.5
1.5
H(f)
1.0
1.0
0,70
0.5
0.5
0.35
0.25
0.20
0.05
0
0.5
1.0
1.5
2.0
2.5
f
0
0.5
1.0
1.5
2.0
2.5
f
53. Структурная схема МСП с ФРК
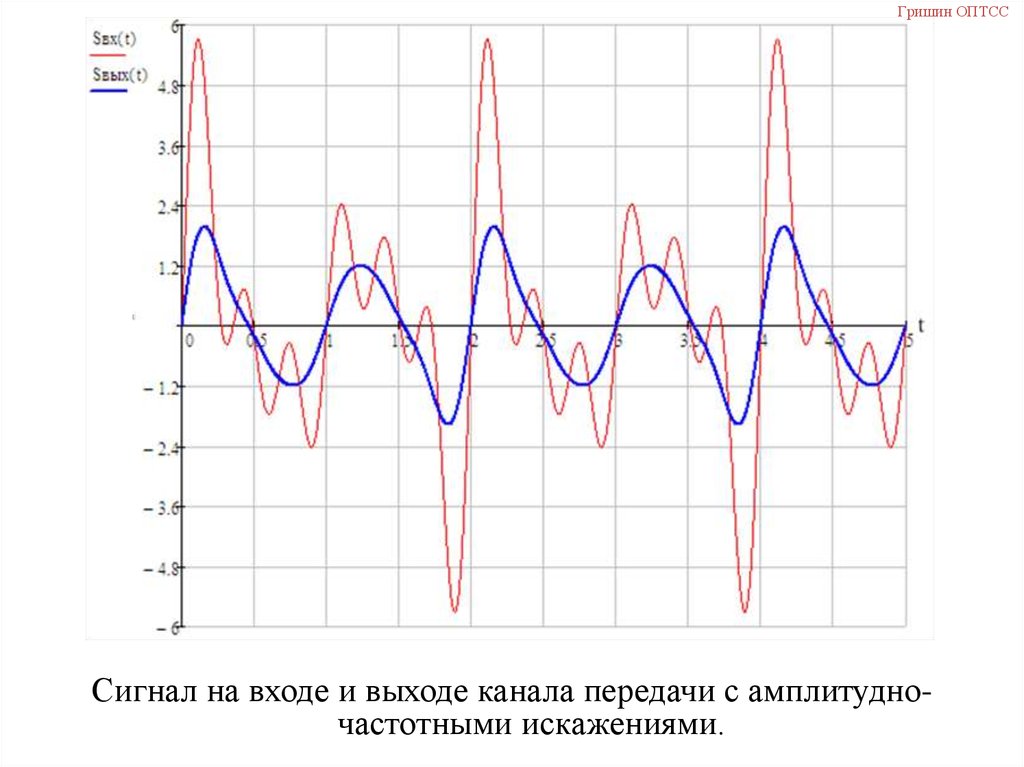
Гришин ОПТСССигнал на входе и выходе канала передачи с амплитудночастотными искажениями.
54. Характеристики канала передачи
Гришин ОПТССАМПЛИТУДНО-ЧАСТОТНЫЕ ИСКАЖЕНИЯ
H ( ) H ( )
Разложение амплитудно-частотной характеристики в ряд Фурье
2
2
2
H ( ) H 0 H1 cos H 2 cos 2 H n cos n ...
T
T
T
2
2
1
T 2 max 2 f max
H ( ) H 0 H1 cos H 2 cos 2 H n cos n ...
к ( ) k 2 n
S вых ( ) S вх ( ) H 0 H n cos n exp( jk )
S ( ) H H cos m exp( jk )
вх
0
n
1
sвых (t )
Sвх ( ) H 0 H n cosn exp j (t k ) d
2
55.
1sвых (t )
Sвх ( ) H 0 exp j (t k ) d
2
Гришин ОПТСС
Hn
Sвх ( ) exp j (t k m) d Sвх ( ) exp j (t k m) d
4
sвх(t)
sвых(t)
t
0
m
m
k
Сигнал на входе и выходе канала передачи с амплитудночастотными искажениями.
56.
ФАЗО-ЧАСТОТНЫЕ ИСКАЖЕНИЯГришин ОПТСС
к ( ) к ( )
Разложение амплитудно-частотной характеристики в ряд Фурье
к ( ) k к1 sin к 2 sin 2 к n sin n ...
к ( ) k кn sin( m )
d к ( )
k m кn cos(m )
d
S вых ( ) S вх ( ) H 0 exp j k кn sin( m )
tгр ( )
1
sвых (t )
Sвх ( ) H 0 exp j k к sin( m ) exp j (t k ) d
2
exp j кn sin( m ) J 0 ( кn ) J1 ( кn ) exp( jm ) J 0 ( кn ) exp( jm )
e
j кn sin( m )
H0
j ( t k )
jm
jm
S
(
)
e
J
(
)
J
(
)
e
J
(
)
e
0
кn
1
кn
1
кn
вх
2
57.
Гришин ОПТССH0
j ( t k )
jm
jm
e
S
(
)
e
J
(
)
J
(
)
e
J
(
)
e
вх
0
кn
1
кn
1
кn
2
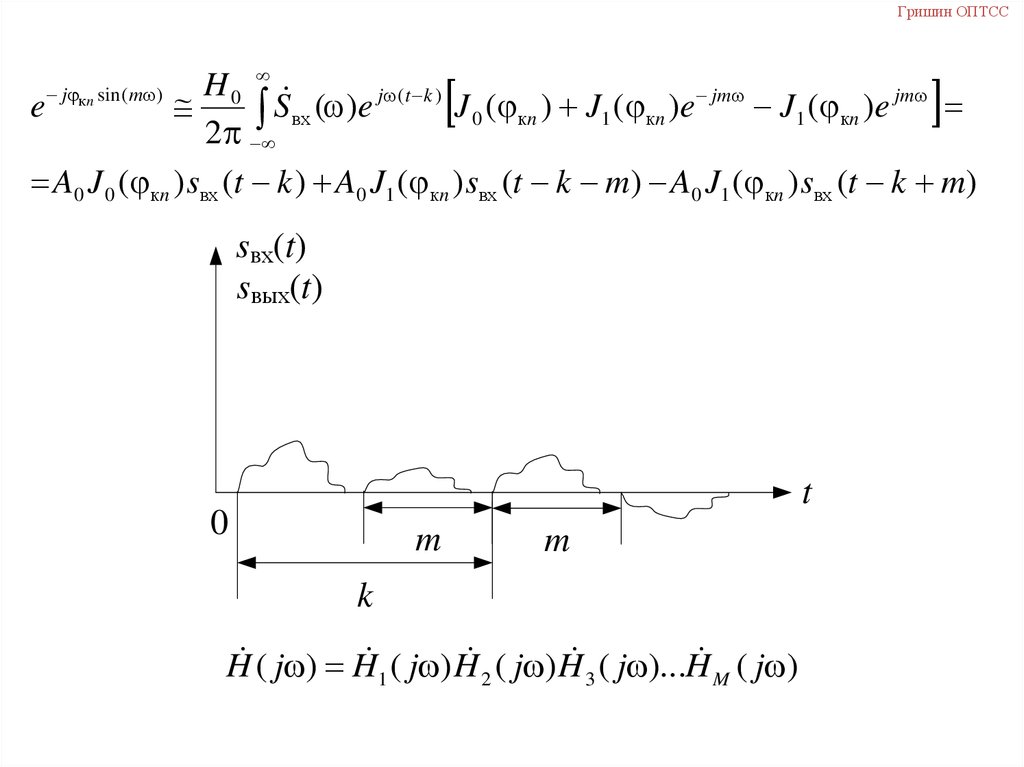
A0 J 0 ( кn ) sвх (t k ) A0 J1 ( кn ) sвх (t k m) A0 J1 ( кn ) sвх (t k m)
j кn sin( m )
sвх(t)
sвых(t)
t
0
m
m
k
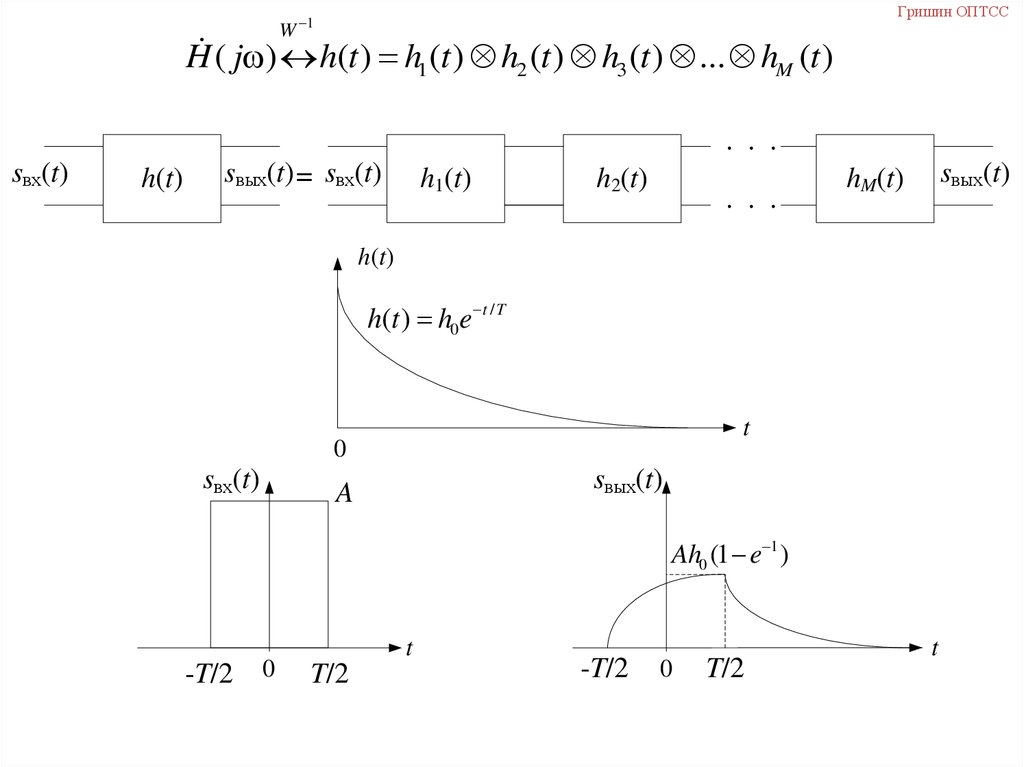
H ( j ) H 1 ( j ) H 2 ( j ) H 3 ( j )...H M ( j )
58.
Гришин ОПТССW 1
H ( j ) h(t ) h1 (t ) h2 (t ) h3 (t ) ... hM (t )
. . .
sвх(t)
h(t)
sвых(t) = sвх(t)
h1(t)
h2(t)
. . .
sвых(t)
hM(t)
h(t)
h(t ) h0e t / T
t
0
sвх(t)
sвых(t)
A
Ah0 (1 e 1 )
-T/2
0
t
T/2
-T/2
0
T/2
t
59.
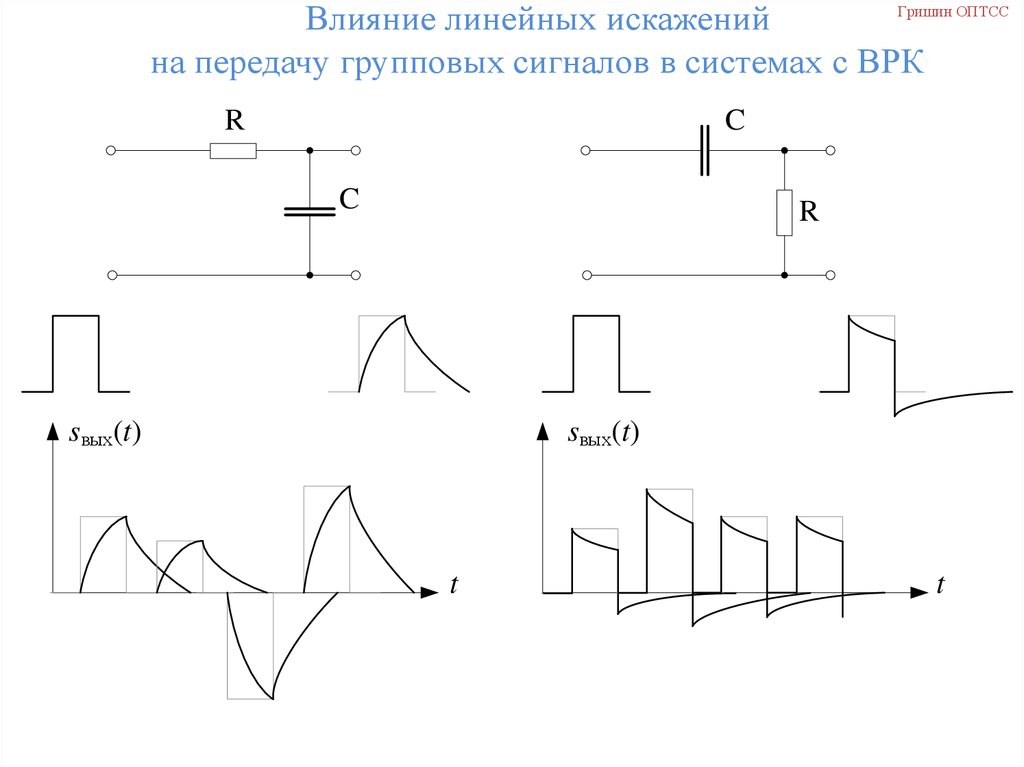
Гришин ОПТССВлияние линейных искажений
на передачу групповых сигналов в системах с ВРК
R
C
C
R
sвых(t)
sвых(t)
t
t
60.
НЕЛИНЕЙНЫЕ ИСКАЖЕНИЯ3
sвх (t ) A cos( t )
sвых (t ) ck sвхk (t )
k 1
3
3
sвых (t ) ck A cos ( t ) Ak cos(k t )
k
k
k 1
k 1
Ak 2 ck Ak
1 k
K kг 10 0.05akг
k 1
Ak ck Ak 1 ck A1
k 1 k 1 k
A1 2 c1 2 c1
ck Ak 1
A1
akг 20 lg K kг 20 lg k 1 20 lg
2 c1
A
N
N
l 1
l 1 m 1
k 1
akг0 p(k 1)
N
sвых (t ) A0 A1 cos(2 f l t ) A2 cos 2 f l f m t
N
N
N
A3 cos 2 f l f m f n t .
l 1 m 1 n 1
N!
C
( N n)!n!
n
N
Гришин ОПТСС
61. Влияние линейных искажений на передачу групповых сигналов в системах с ВРК
Основные параметры выходного сигналаa
Aa
Na
j
c1 Aj
1
c2 A2j
2
1
c3 A3j
2
c2 Aj Ai
3
c3 A2j Ai
4
3
c3 Aj Ai Ak
2
N
2 j
3 j
i j
2 i j
i j k
N
N
N ( N 1)
2 N ( N 1)
N ( N 1)( N 2)
Гришин ОПТСС
62.
63.
64.
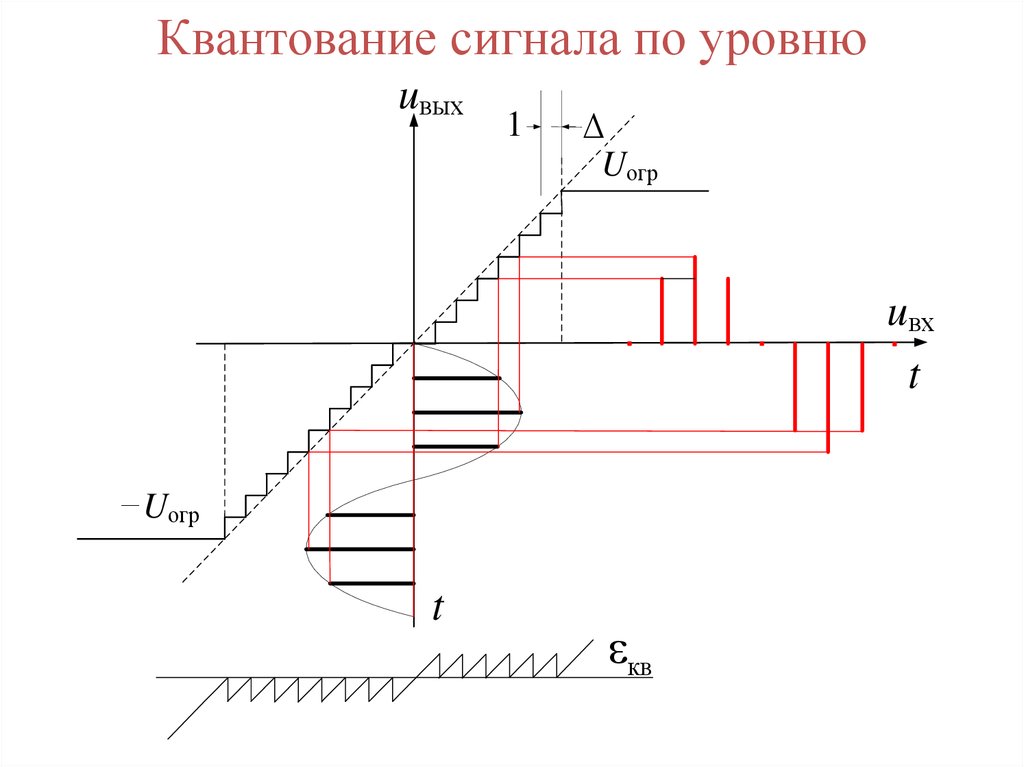
Квантование сигнала по уровнюuвых
1
Δ
Uогр
uвх
t
−Uогр
t
кв
65.
ИПСК
ОКУ
–1
К кодеру
Опознаватель
знака
Квантующее устройство для
передачи двухполярных сигналов
66. Квантование сигнала по уровню
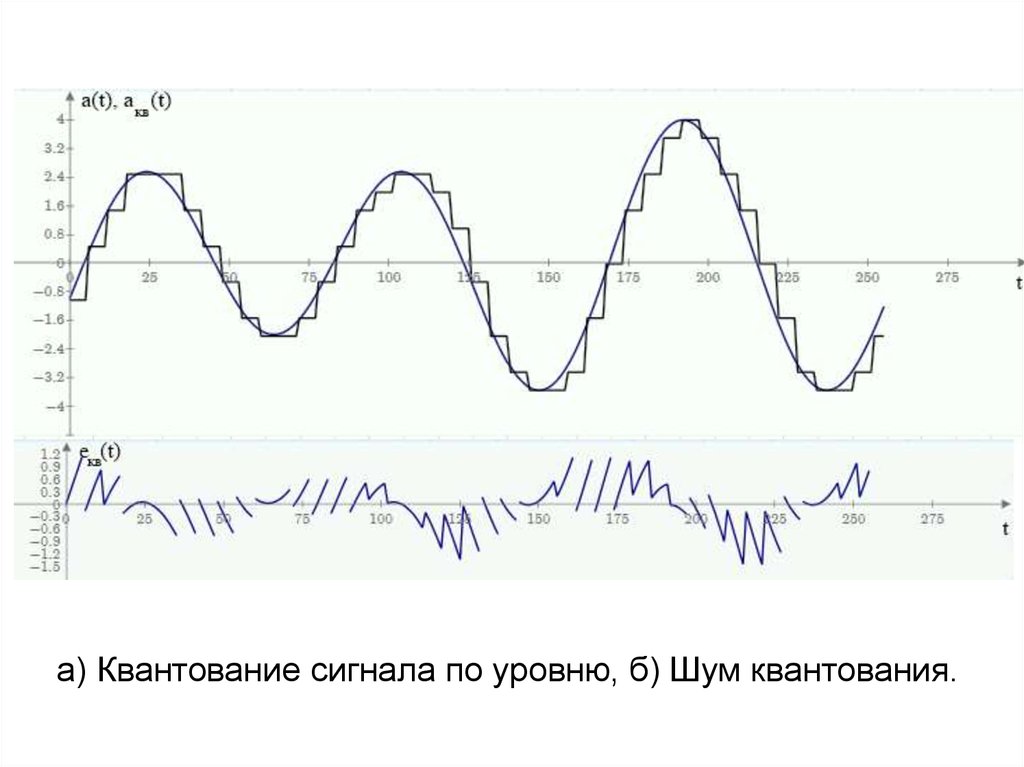
а) Квантование сигнала по уровню, б) Шум квантования.67.
Мощность шумов квантованияT
T M
кв lim (t )dt lim
T 0
кв,m
2
кв
1
lim
T T
2
кв, m
(t )dt кв,m
T 0 m 0
t m , a / 2
t m ,b / 2
2
2
кв, m
кв, m
t m , a / 2
t m ,b / 2
(t )dt
t m , z / 2
2
кв, m
m , a t m , z / 2
t m,a t m , z 1
lim
T
t
T
M
m 0
(t )dt
t m , z / 2
2
кв, m
t m , z / 2
(t )dt
2
m 2
1
t dt
(t )dt pa
t m ,a t m , z / 2 t m ,a
t m , z / 2
a(t)
ai+1
ai
t
1
2
3
...
z
68.
a(t)Δm
w(a)
t
pm (U m ) m
кв,m
U m / 2
U m / 2
2
кв, m
(U ) (U )dU (U m )
3m
2m
(U m ) z dz (U m )
pm
12
12
/2
M
3m M
2m 2
кв (U m )
pm
12 m 1 12 12
m 1
/2
U m / 2
U m / 2
(U U m ) 2 dU
2
M
U огр
m 1
U огр
pm
(U m )dU 1
69. Мощность шумов квантования
Выбор числа уровней квантованияpср Т НОУ 13 15 дБ, 4,5 5,5 дБ kп 16 18 дБ
pб pср Т НОУ 3 U пик U 0dec 0,05 pср kп ,
Для биполярных сигналов
2
U
1
2 U огр
2 U огр
огр
P
кв
M
1
2
3
M
2
M 2U аб
Pc
10 lg 10 lg 3 2 10 lg 3M 2 pаб pcp Т НОУ 3 kп
U
Pкв
огр
Для униполярных сигналов
2
U огр
U
1 огр
M
Pкв
12 M 2
2
M 2U аб
Pc
2
10 lg 10 lg 12
10
lg
12
M
pаб pcp Т НОУ 3 kп
2
U
Pкв
огр
70.
Выбор числа уровней квантованияa(t ) aкв (t ) кв (t )
a(t )
кв(t)
aкв (t) a(i t ) aˆ (t )
Б
А
В
2
S
( j )d
в
0
н
2
2
S
(
j
)
d
S
( j )d ;
в
2
S
( j )d
Pаб, А Pаб, Б
0
0,50 д
кв , А кв , Б
2
2
S
(
j
)
d
S
кв
кв ( j )d
0
0 , 5 д
0 , 5 д
0 , 5 д
0
в
0
,
5
2
2
д
S
(
j
)
d
S
кв ( j ) d
кв
в н н
0
2
S
( j )d
Pаб, А
Pаб, В
н
в
кв , А 0,5 д
0,5 д кв , В
2
S кв ( j )d
н
Pаб, В
Pвых
0,5 f д Pвых
0,5 д кв , В кв ,вых f в f н кв ,вых
71. Выбор числа уровней квантования
20,5 f д 3M 2U аб
Pc
,А
10 lg 10 lg
2
f f U
Pкв
в
н
огр
,
Б
0,5 f д
10 lg 3M pаб pcp Т НОУ 3 kп 10 lg
fв fн
2
1
2
0,5 f д U аб, А
M dec 0,05 10 lg 3
2
f f U
в
н
огр
,
Б
0,5 f д
dec 0,05 pаб pcp Т НОУ 3 kп 10 lg 3
f
f
в
н
72. Выбор числа уровней квантования
Цифро-аналоговый преобразовательuоп
X x1 , x2 , x3 ,..., xN ,
ЦАП
x1
1
x2
2
u uоп D,
x3
3
x4
4
0
x1 x2 x3
xN
где D 2 3 ... N , xn
2 2 2
2
1
u1
xN
N
u2
u
I0
2U оп x1 x2 x3
xN
...
,
2
3
N
R 2 2 2
2
x
x
x x
U I 0 R0 U оп 1 22 33 ... NN
2
2 2 2
2N 1
U оп
U max U оп N ; N
2
2
73. Выбор числа уровней квантования
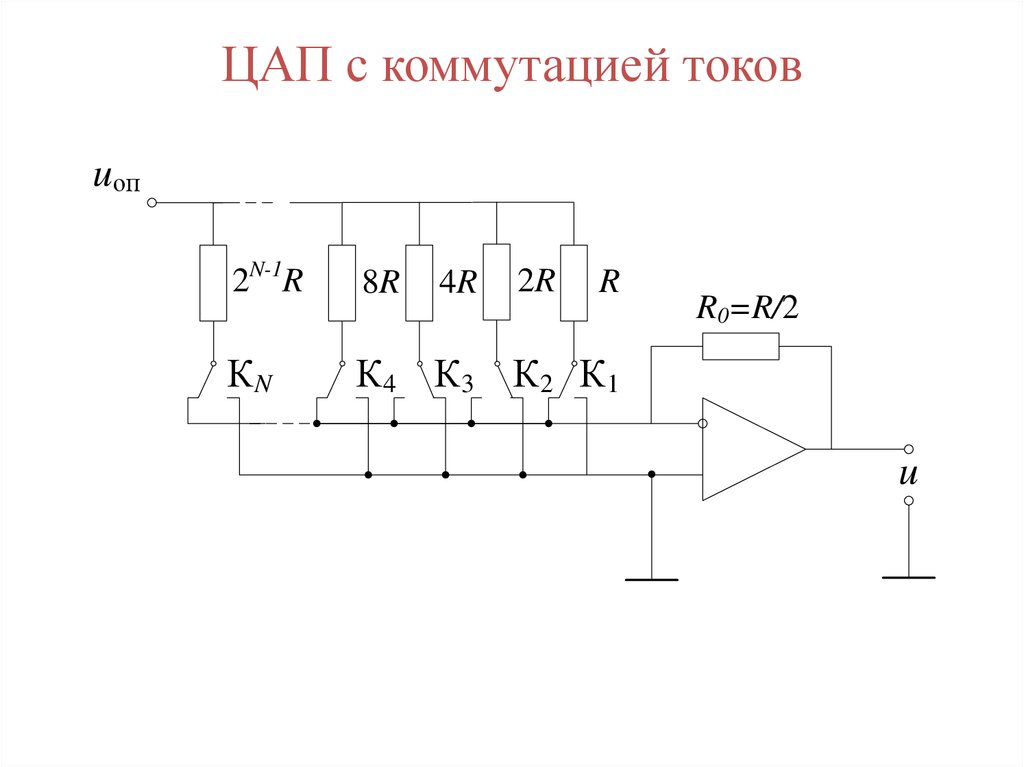
ЦАП с коммутацией токовuоп
2N-1R
8R
КN
К4 К 3 К 2 К 1
4R
2R
R
R0=R/2
u
74. Цифро-аналоговый преобразователь
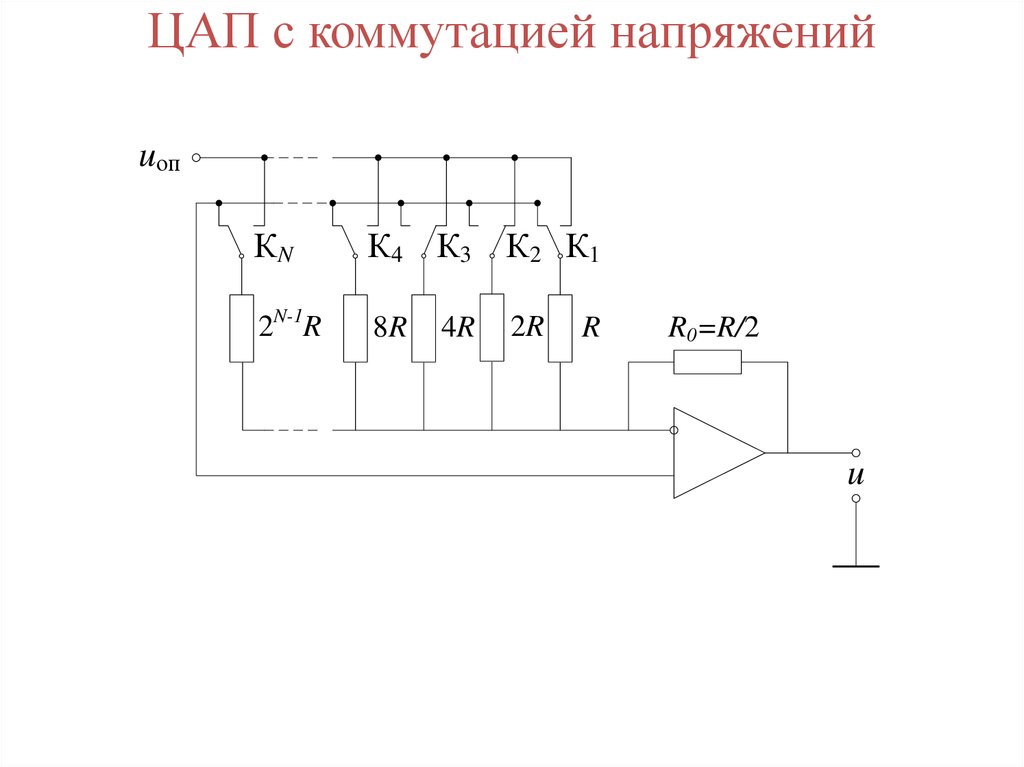
ЦАП с коммутацией напряженийuоп
КN
К4 К 3 К 2 К 1
2N-1R
8R
4R
2R
R
R0=R/2
u
75. ЦАП с коммутацией токов
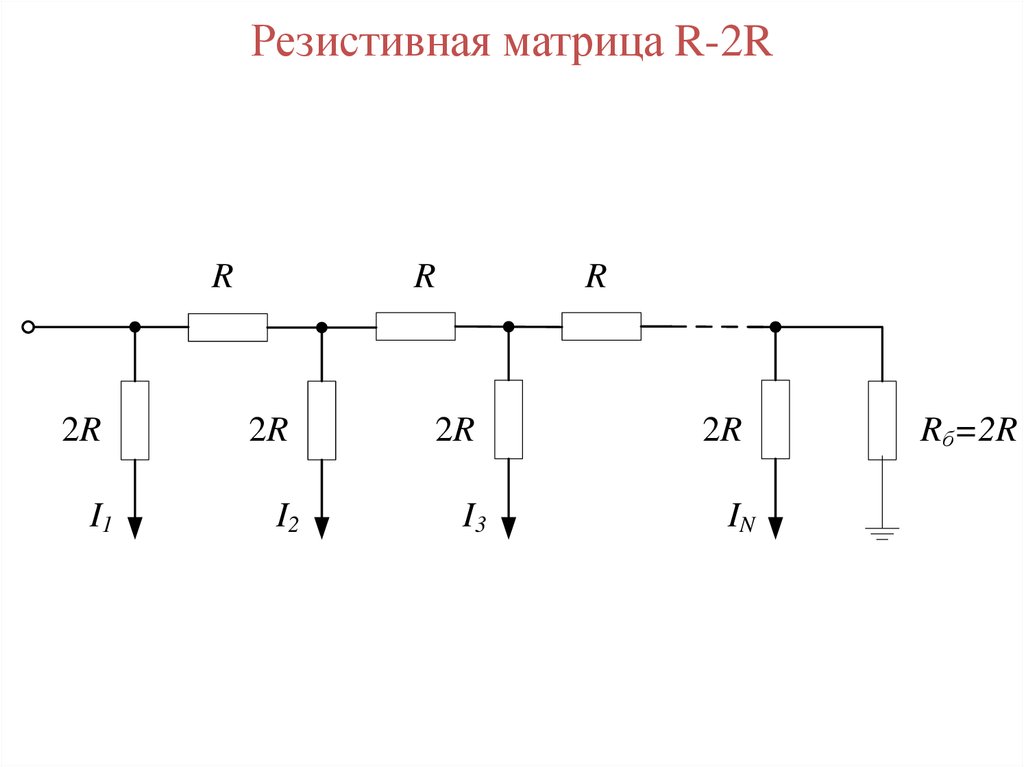
Резистивная матрица R-2RR
2R
I1
R
2R
I2
R
2R
I3
2R
IN
Rб=2R
76. ЦАП с коммутацией напряжений
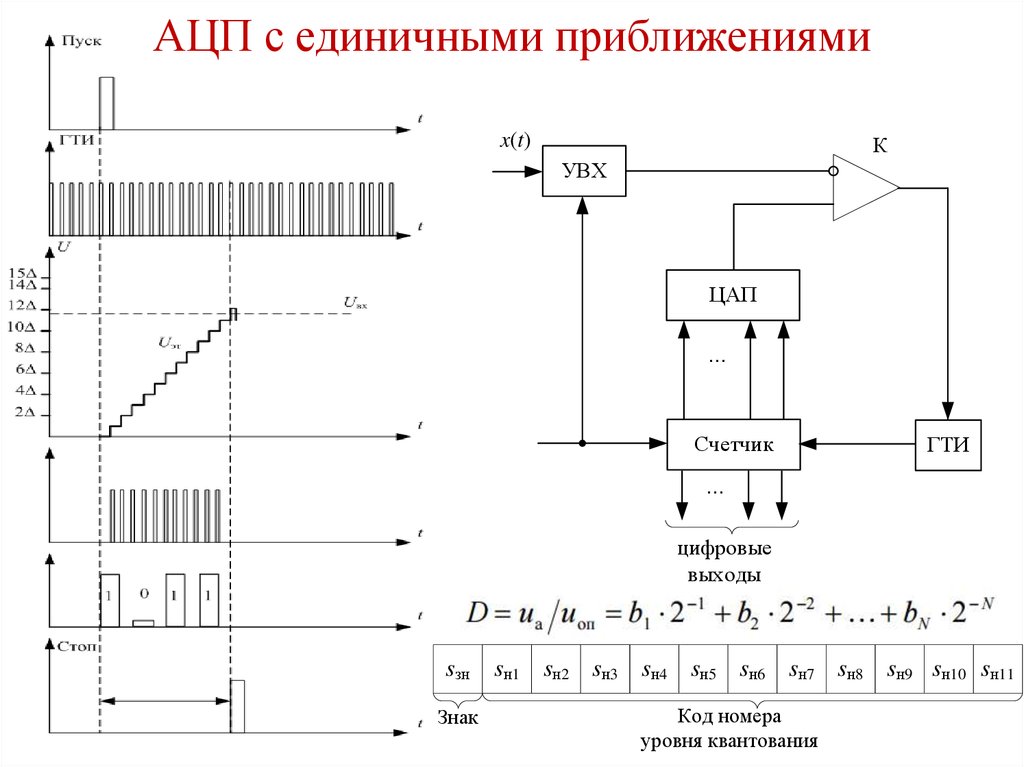
АЦП с единичными приближениямиx(t)
К
УВХ
ЦАП
...
Счетчик
ГТИ
...
цифровые
выходы
sзн
Знак
sн1 sн2 sн3 sн4 sн5 sн6 sн7 sн8 sн9 sн10 sн11
Код номера
уровня квантования
77. Резистивная матрица R-2R
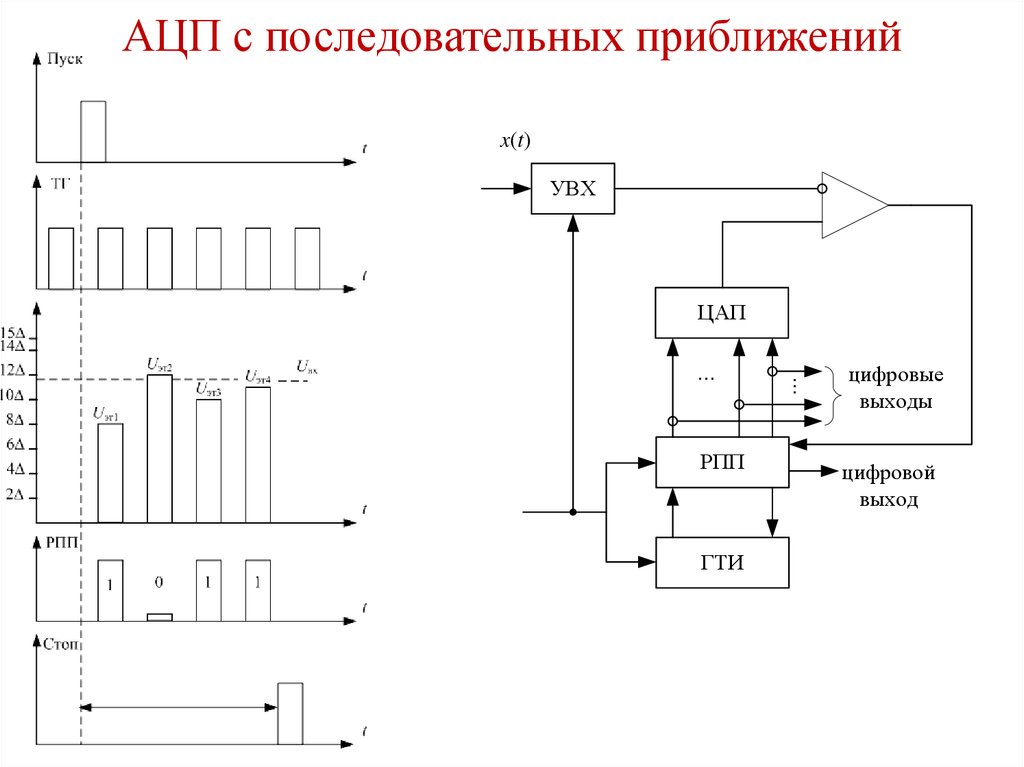
АЦП с последовательных приближенийx(t)
УВХ
...
РПП
ГТИ
...
ЦАП
цифровые
выходы
цифровой
выход
78. АЦП с единичными приближениями
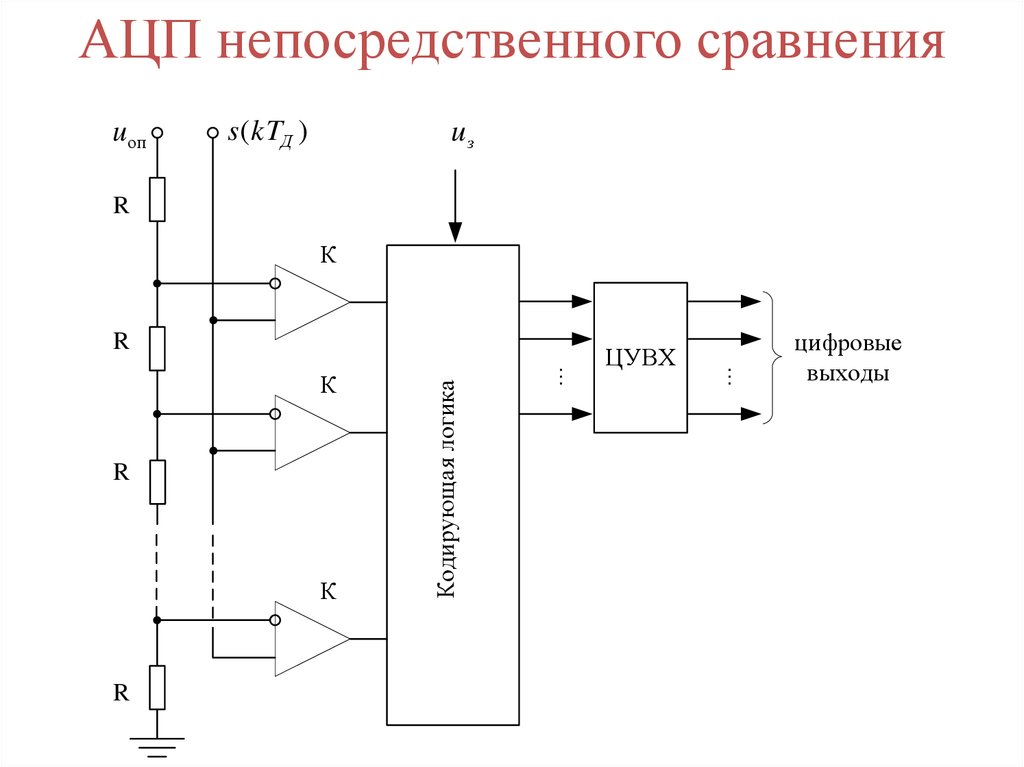
АЦП непосредственного сравненияu оп
s (kTД )
uз
R
R
К
R
...
К
Кодирующая логика
R
ЦУВХ
...
К
цифровые
выходы
79. АЦП с последовательных приближений
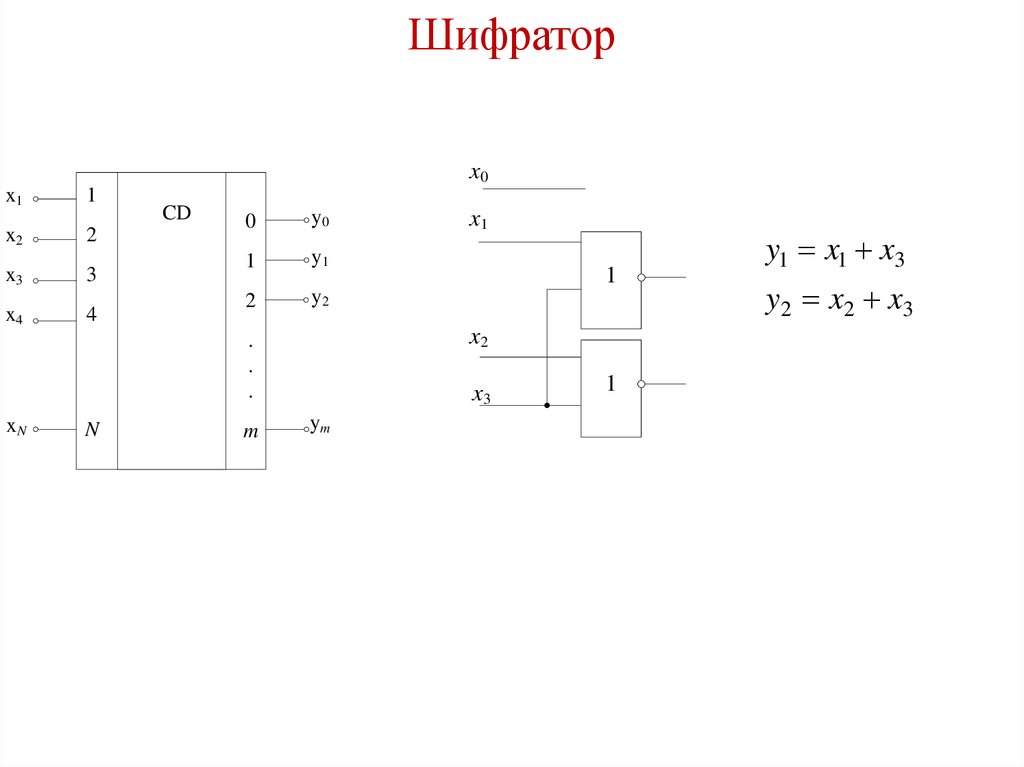
Шифраторx0
x1
1
x2
2
x3
3
x4
4
CD
0
y0
1
y1
2
y2
N
m
1
x2
.
.
.
xN
x1
x3
ym
1
y1 x1 x3
y2 x2 x3
80.
Неравномерное квантованиеm
m
Линейный
тракт
m
m
Линейный
тракт
ПКпр
ПКпд
m
Линейный
тракт
m
81.
Амплитудные характеристикикомпрессора и экспандера
U вых к U вх к U вых э U вх э 1
82. Неравномерное квантование
83. Амплитудные характеристики компрессора и экспандера
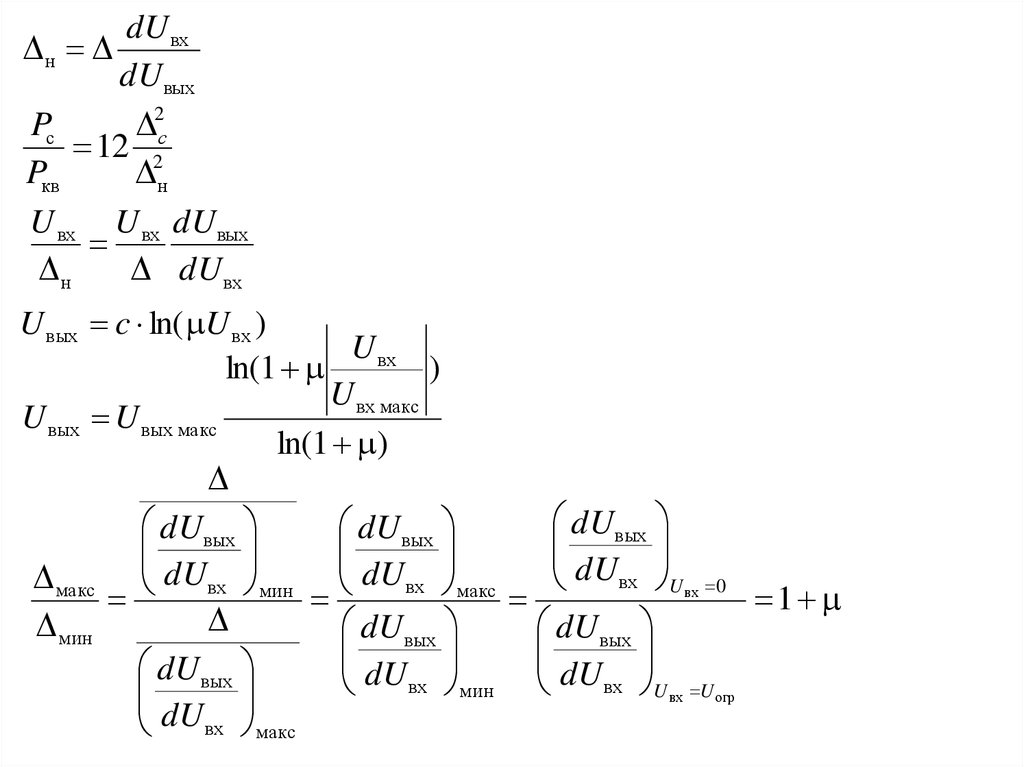
dUвхн
dUвых
Pс
2с
12 2
Pкв
н
U вх U вх dUвых
н
dUвх
U вых c ln( U вх )
U вх
ln(1
)
U вх макс
U вых U вых макс
ln(1 )
dU вых
dU вых
dU вых
макс dU вх мин dU вх макс
dU вх U вх 0
1
мин
dU вых
dU вых
dU вых
dU вх мин dU вх U вх U огр
dU вх макс
84.
Uвых э 1U / U вх макс
ln(1 x )
y
ln(1 )
ln 1
2
U вх
w(U вх )dU вх
Pш.кв
1
2 2
3M
U
огр
U огр
c U вх ; Uвх k c макс ; Pc k c2 ; Pогр k 2 c2 макс
U
2
огр
2
U огр
Pогр ln 1
P
c
1
2 2
3M
P
огр
2
Pш.кв
2
Pc
с
Pогр k с макс
c2 3M 2 2
Aкв н 10 lg
k
2
2
с макс
c
ln(1 ) 1
k
с
макс
2
85.
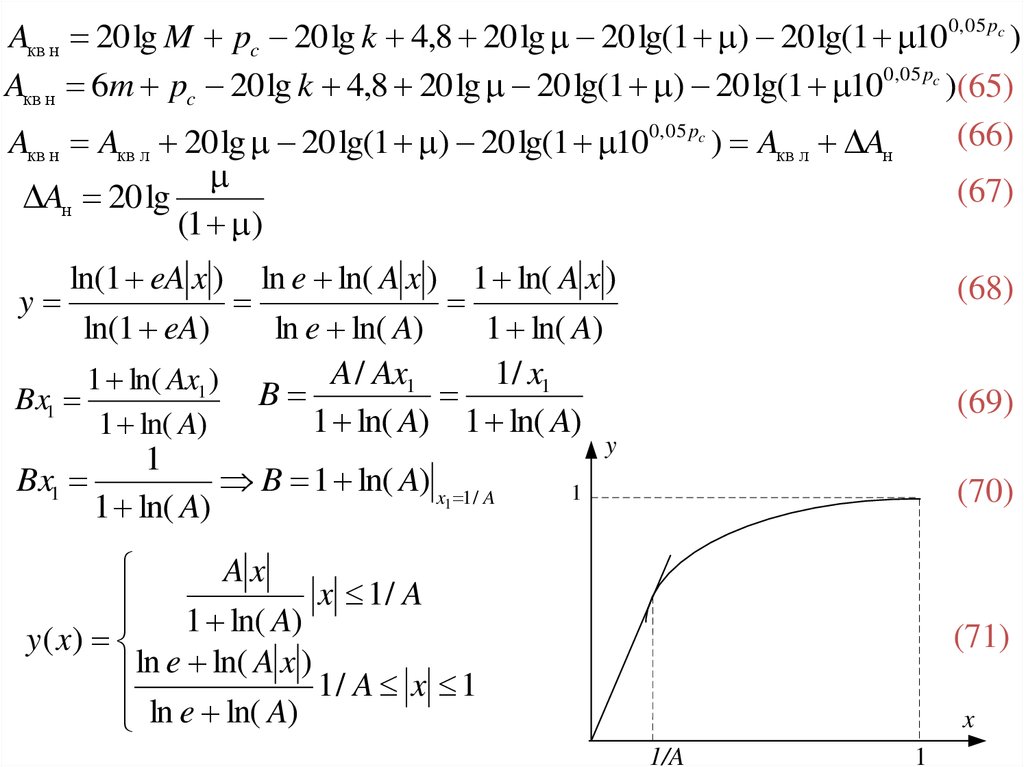
Aкв н 20 lg M pc 20 lg k 4,8 20 lg 20 lg(1 ) 20 lg(1 100,05 pc )Aкв н 6m pc 20 lg k 4,8 20 lg 20 lg(1 ) 20 lg(1 100,05 pc )(65)
(66)
Aкв н Aкв л 20 lg 20 lg(1 ) 20 lg(1 100,05 pc ) Aкв л Aн
(67)
Aн 20 lg
(1 )
ln(1 eA x ) ln e ln( A x ) 1 ln( A x )
y
ln(1 eA)
ln e ln( A)
1 ln( A)
1 ln( Ax1 ) B A / Ax1 1/ x1
Bx1
1 ln( A) 1 ln( A)
1 ln( A)
y
1
Bx1
B 1 ln( A) x 1/ A
1
1
1 ln( A)
(68)
(69)
(70)
Ax
x 1/ A
1 ln( A)
y ( x)
ln e ln( A x ) 1 / A x 1
ln e ln( A)
(71)
x
1/A
1
86.
87.
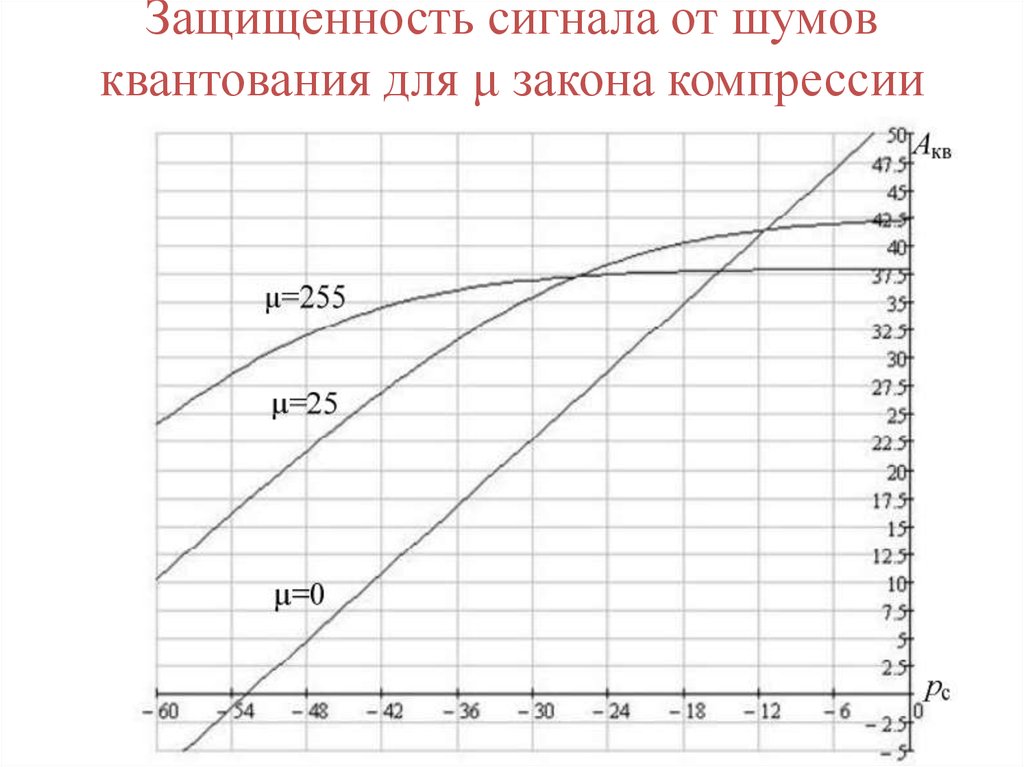
Защищенность сигнала от шумовквантования для μ закона компрессии
88.
Нелинейное кодированиеUвых
128Δ
112Δ
96Δ
80Δ
64Δ
48Δ
32Δ
16Δ
Uвх
0
128Δ
1/16
0
512Δ
1024Δ
1/4
16Δ 32Δ
2048Δ
1
1/2
64Δ
128Δ
89. Защищенность сигнала от шумов квантования для μ закона компрессии
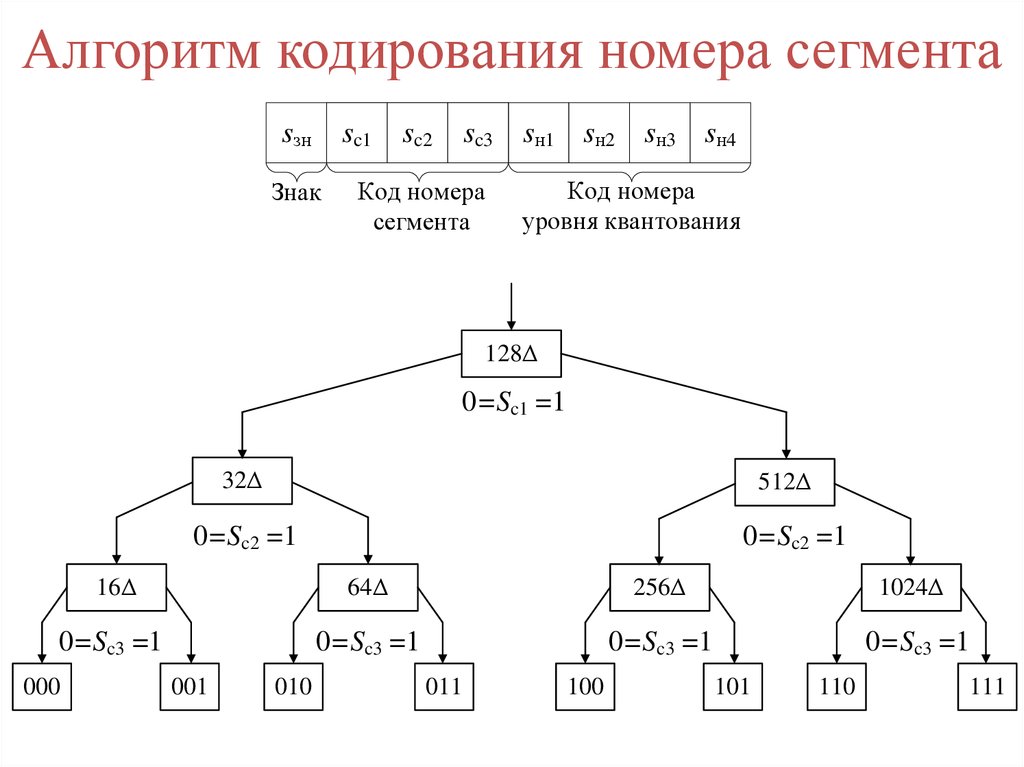
Алгоритм кодирования номера сегментаsзн
sc1
Знак
sc2
sc3
sн1 sн2 sн3 sн4
Код номера
сегмента
Код номера
уровня квантования
128Δ
0=Sc1 =1
32Δ
512Δ
0=Sc2 =1
0=Sc2 =1
16Δ
64Δ
256Δ
1024Δ
0=Sc3 =1
0=Sc3 =1
0=Sc3 =1
0=Sc3 =1
000
001
010
011
100
101
110
111
90. Нелинейное кодирование
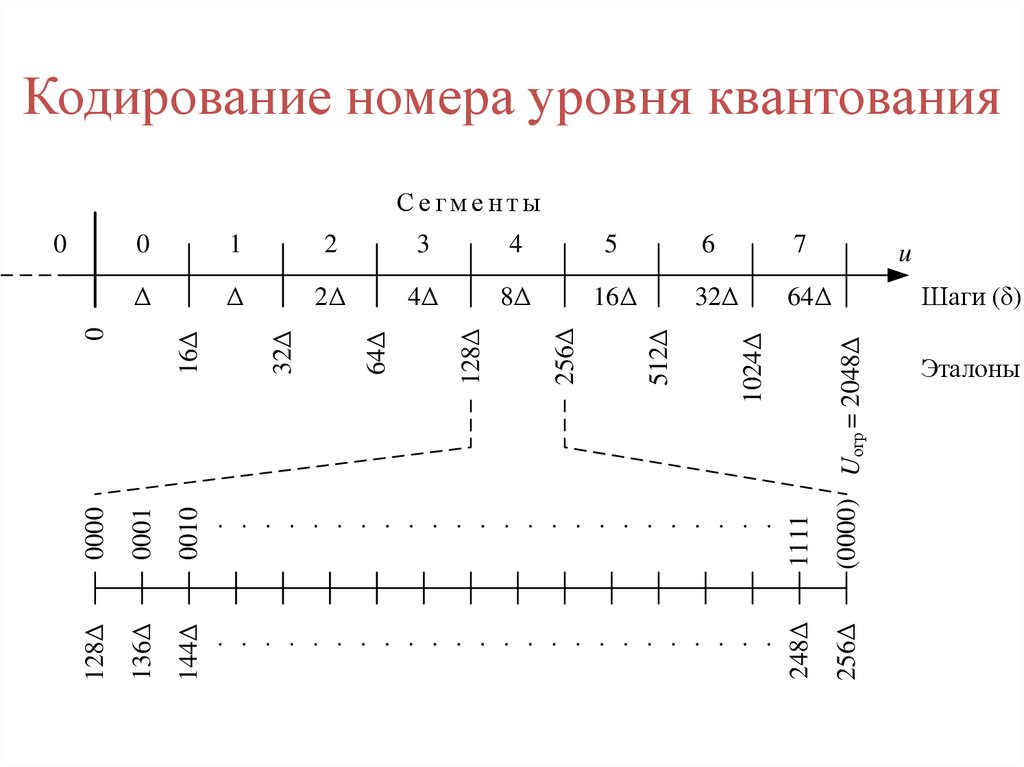
Кодирование номера уровня квантованияСегменты
6
7
Δ
Δ
2Δ
4Δ
8Δ
16Δ
32Δ
64Δ
0001
0010
1111
(0000) Uогр = 2048Δ
136Δ
144Δ
248Δ
256Δ
Шаги (δ)
0000
16Δ
u
128Δ
1024Δ
5
512Δ
4
256Δ
3
128Δ
2
64Δ
1
32Δ
0
0
0
Эталоны
91. Алгоритм кодирования номера сегмента
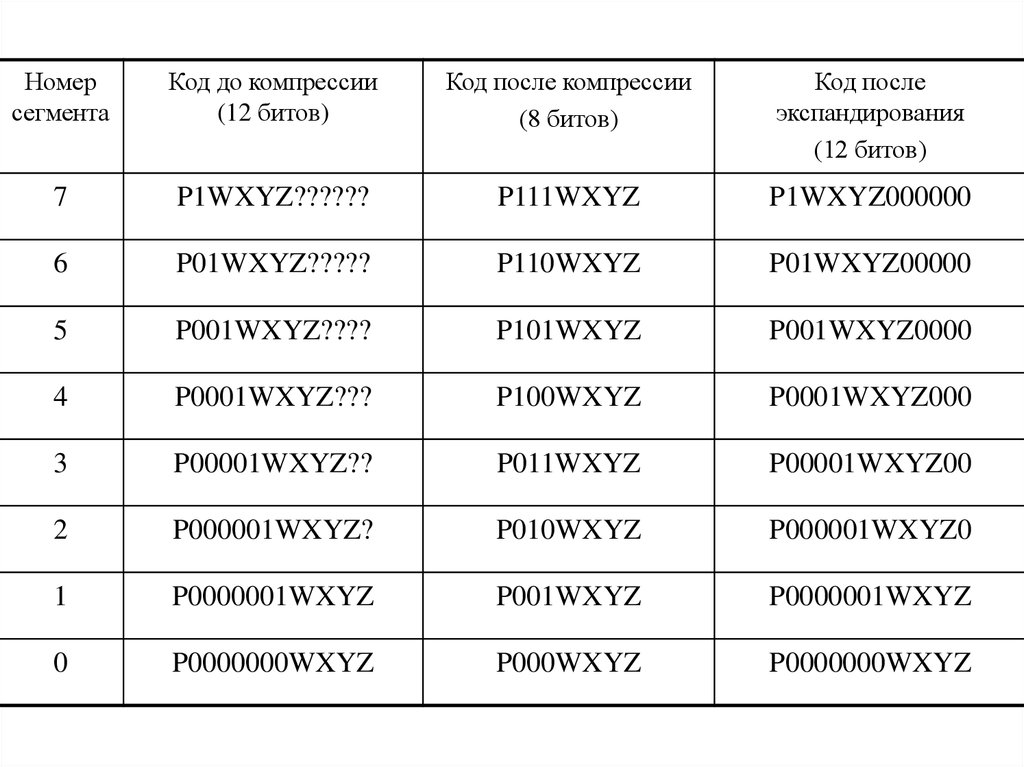
Номерсегмента
Код до компрессии
(12 битов)
Код после компрессии
(8 битов)
Код после
экспандирования
(12 битов)
7
P1WXYZ??????
P111WXYZ
P1WXYZ000000
6
P01WXYZ?????
P110WXYZ
P01WXYZ00000
5
P001WXYZ????
P101WXYZ
P001WXYZ0000
4
P0001WXYZ???
P100WXYZ
P0001WXYZ000
3
P00001WXYZ??
P011WXYZ
P00001WXYZ00
2
P000001WXYZ?
P010WXYZ
P000001WXYZ0
1
P0000001WXYZ
P001WXYZ
P0000001WXYZ
0
P0000000WXYZ
P000WXYZ
P0000000WXYZ
92. Кодирование номера уровня квантования
93.
Схема ИКМ-30Групповое оборудование
Индивидуальное оборудование
УНЧ пд
ОА
кодер
АИМ-1
ФНЧ пд
АИМ2
...
dB
СУВ от АТС
СУВ 1
m
Р1
30
ЛТр1
ПКпд
... Р8
Iдп
СУпд
СУпр
...
ДЦ
ГО пд
ДР
ДК
ДЦ
Ц15
КИ31
КИ0
СУВ 2
СУВ к АТС
2
ФЛС
Ц0
+
ФС
ДР
ДК
...
...
30
2
dB
...
ДП
ГО пр
Пр. синхр
ВТЧ
m
УНЧ пр
ФНЧ пр
ВС
Индивидуальное оборудование
Декодер
Групповое оборудование
ПКпр
ЛТр2
94.
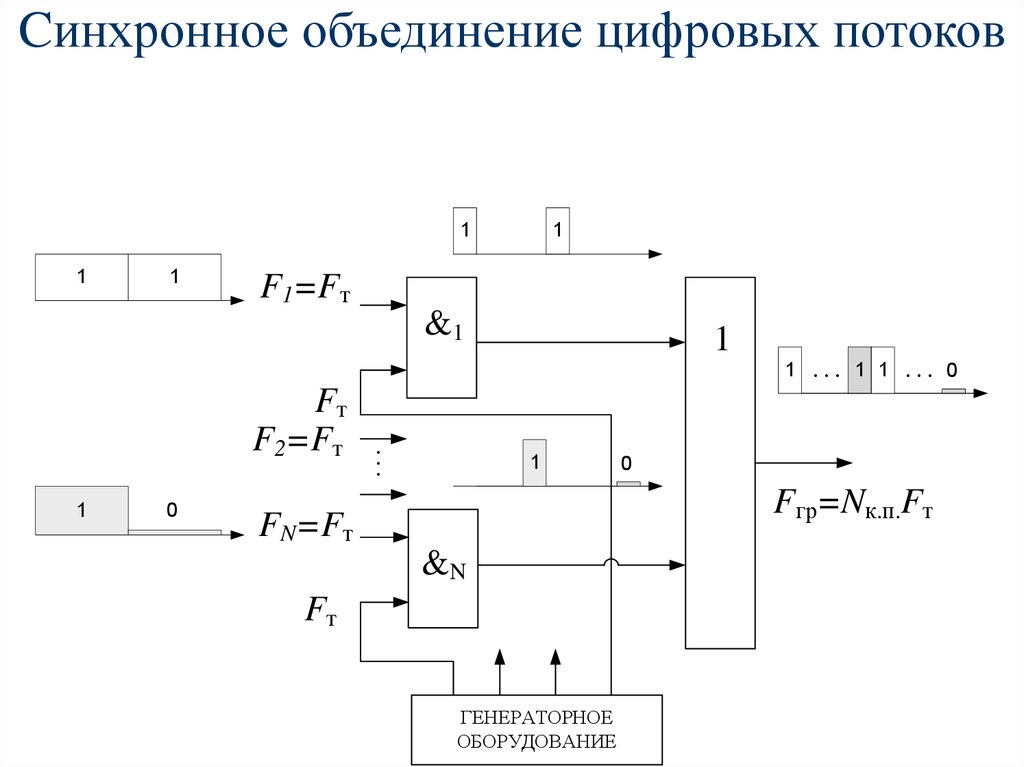
Cинхронное объединение цифровых потоков1
F1=Fт
&1
1
1
1
0
…
Fт
F2=Fт
1
…
1
1 1
…
1
1
0
Fгр=Nк.п.Fт
FN=Fт
&N
Fт
ГЕНЕРАТОРНОЕ
ОБОРУДОВАНИЕ
0
95.
Блок синхронного объединения1
1
0
FN=Fт
F’т
1
Fгр
&N
б)
F’т
F’т=Fз
Э
M гр
M гр M сс
1
0
F’т
ЗУ
1
ГЕНЕРАТОРНОЕ
ОБОРУДОВАНИЕ
с/с
1 1
С
…
от ГО
а)
0
С 1
…
1
&1
…
F2=Fт
F’т >Fт
ЗУ
…
F1=Fт
1
0
1 1
…
1
1
1
…
…
1
б)
1
…
а)
0
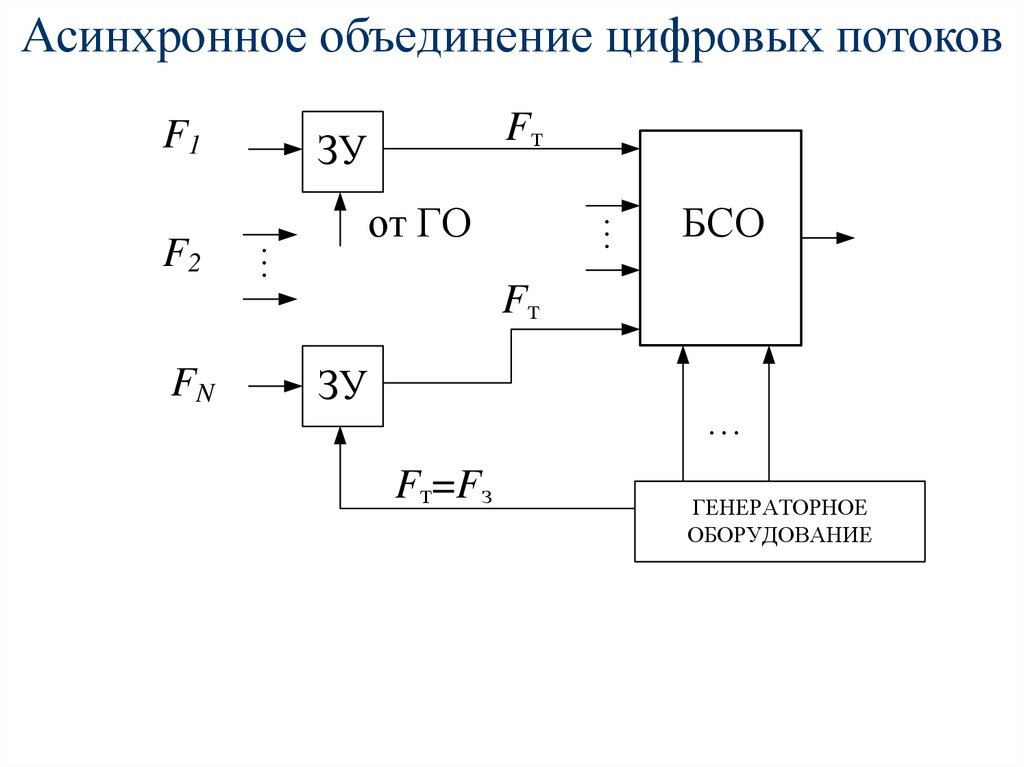
96.
Асинхронное объединение цифровых потоковF1
от ГО
…
FN
ЗУ
…
F2
Fт
БСО
Fт
ЗУ
…
Fт=Fз
ГЕНЕРАТОРНОЕ
ОБОРУДОВАНИЕ
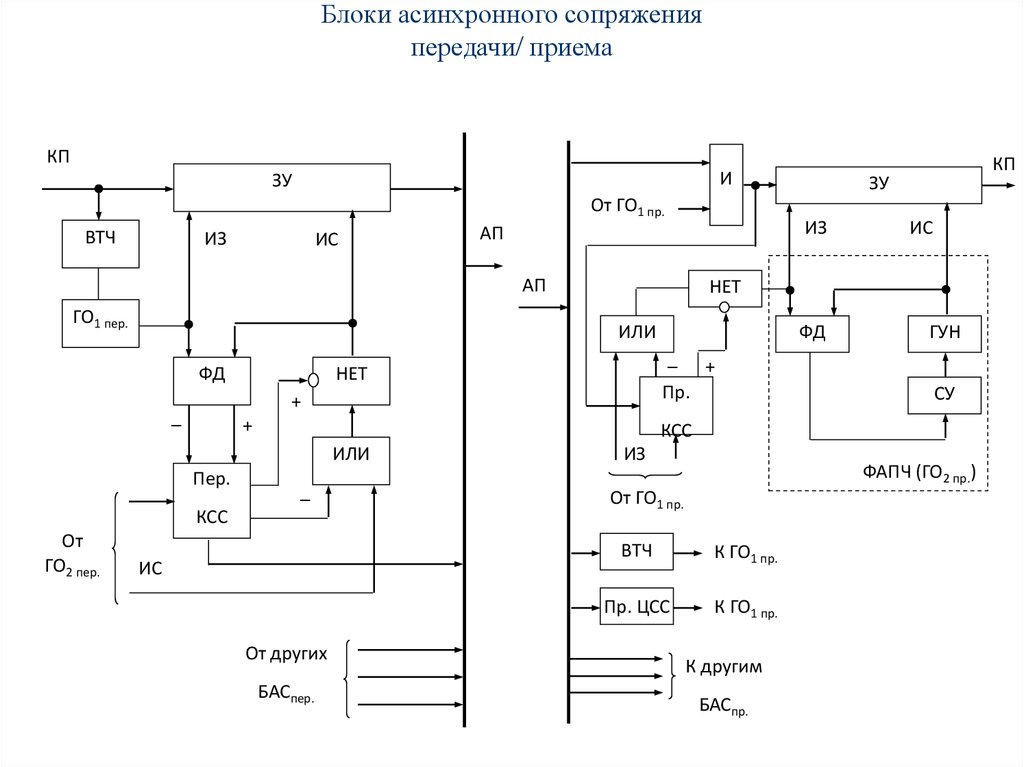
97.
Блоки асинхронного сопряженияпередачи/ приема
КП
И
ЗУ
От ГО1 пр.
ВТЧ
ИЗ
ИС
ИЗ
АП
АП
ГО1 пер.
+
Пер.
КСС
ГУН
СУ
КСС
ИЛИ
От
ГО2 пер.
ФД
– +
Пр.
НЕТ
+
–
ИС
НЕТ
ИЛИ
ФД
КП
ЗУ
–
ИС
От других
БАСпер.
ИЗ
ФАПЧ (ГО2 пр.)
От ГО1 пр.
ВТЧ
К ГО1 пр.
Пр. ЦСС
К ГО1 пр.
К другим
БАСпр.
98.
f1 – f2ДС
ДС
f1 – f2
ДС
ДС
ДС
f1 – f2
ДС
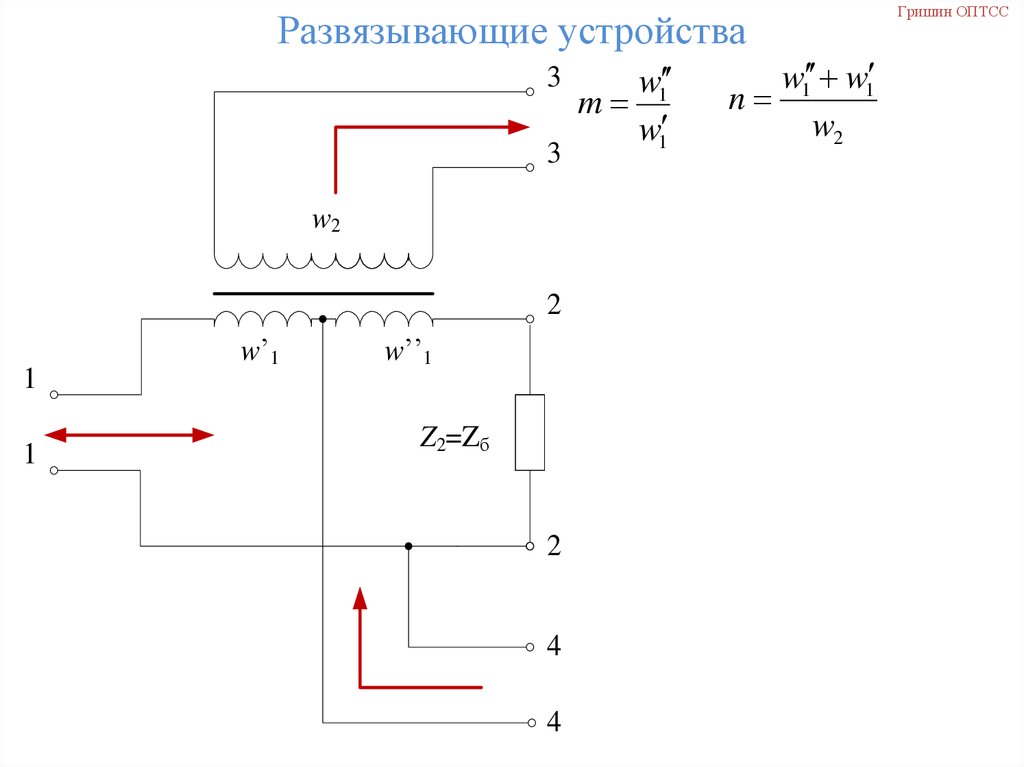
99.
Развязывающие устройства3
3
w2
2
1
1
w’1
w’’1
Z2=Zб
2
4
4
w1
m
w1
w1 w1
n
w2
Гришин ОПТСС
100.
Условие баланса дифференциальной системыZ3
3
3
w2
1
I1w1 I 2 w1
w’1
w’’1
2
4
Zг
Z1
1
Eг
U 4 w1 U 4 mw1
Z1
Zб
4
2
2
4
1
I1 U 4 / Z1 I 2 U 4 / Z б
Z б mZ1
Zб
1
Z1
Гришин ОПТСС
4
Z3 0
Z3
Z14
w1 / w2 2
Zб
2
Z3
Z 42
w1 / w2 2
Z1Z б
mZ1
Z4
Z1 Z б 1 m
101.
Гришин ОПТССU Z1
Z1
P4
m 1
10 lg 10 lg
a41 10 lg 10 lg
P1
m
U Z4
Z4
2
4
2
4
U 42 Z б
Zб
P4
10 lg 10 lg m 1
a42 10 lg 10 lg 2
P2
U 4 Z4
Z4
Z3
Z1 Z б Z1 (1 m)
2
n
n2
3
Zг
Eг
3
3
2
1
4
1
Z3
U
3
n
2
4
nU
Z1
1
U1 Z1
Zб
Z4
4
2
1
4
Zб
U2
2
102.
Гришин ОПТССnU3
U 32 P I 2 Z P I 2 Z
I1
P3
1
1 1
2
1 б
Z1 Z б
Z3
2
P3
Z1 Z б
a31 a13 10 lg 10 lg
10 lg( m 1)
P1
nZ1Z3
P3
Z1 Z б
m 1
a32 a23 10 lg 10 lg
10 lg
P2
nZб Z3
m
2
P1 P2 P3 P4
P1
P3 P1dec( 0.1a31)
1 m
mP1
P4 P1dec( 0.1a41)
1 m
P1
mP1 (1 m) P1
P3 P4
P1 P2 0
1 m 1 m
1 m
a21 a12 10 lg P1 / P2
103.
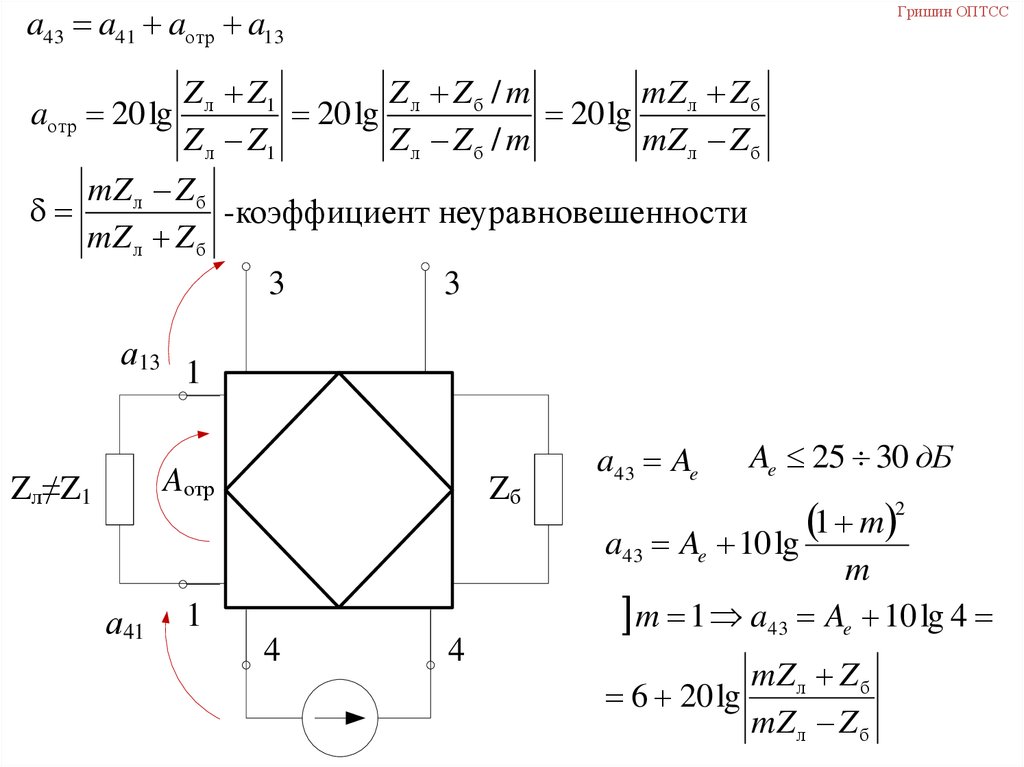
a43 a41 aотр a13Гришин ОПТСС
Z л Z1
Z л Zб / m
mZ л Z б
aотр 20 lg
20 lg
20 lg
Z л Z1
Z л Zб / m
mZ л Z б
mZ л Z б
-коэффициент неуравновешенности
mZ л Z б
3
3
а13
1
Aотр
Zл≠Z1
Zб
a43 Ae
a43 Ae
а41
1
4
4
Ae 25 30 дБ
2
1 m
10 lg
m
m 1 a43 Ae 10 lg 4
mZ л Z б
6 20 lg
mZ л Z б
104.
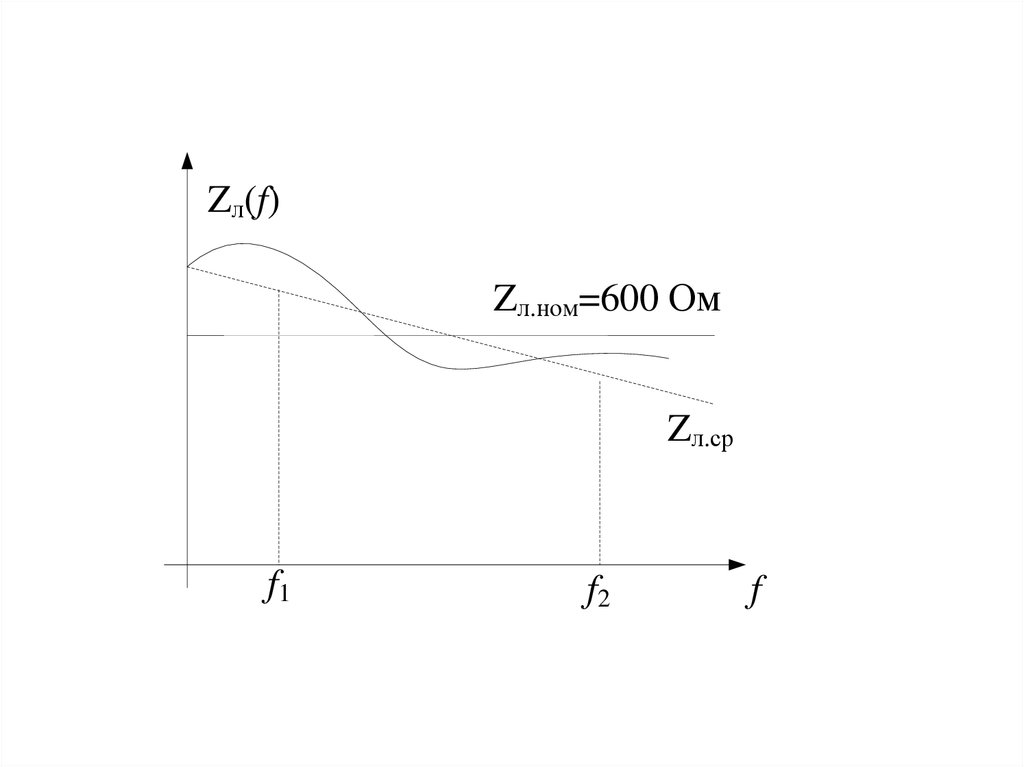
Zл(f)Zл.ном=600 Ом
Zл.ср
f1
f2
f
105.
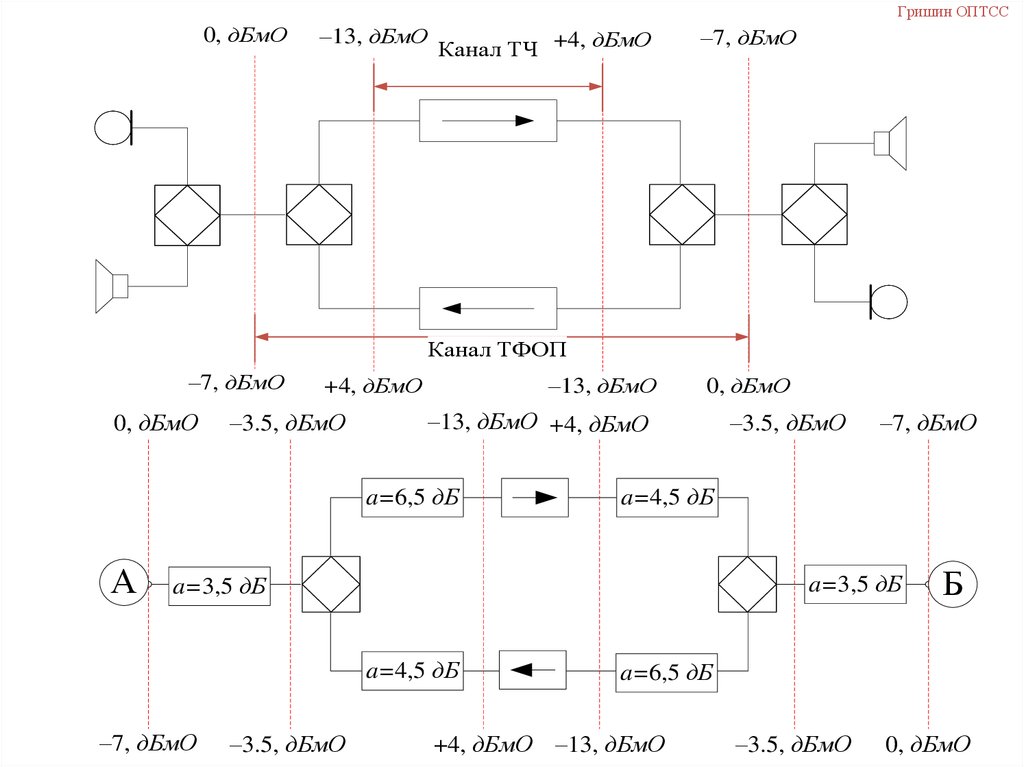
Гришин ОПТСС0, дБмО
–13, дБмО
Канал ТЧ +4, дБмО
–7, дБмО
Канал ТФОП
–7, дБмО
0, дБмО
+4, дБмО
–3.5, дБмО
–13, дБмО
–13, дБмО +4, дБмО
a=6,5 дБ
А
0, дБмО
a=3,5 дБ
a=4,5 дБ
–3.5, дБмО
–7, дБмО
a=4,5 дБ
a=3,5 дБ
–7, дБмО
–3.5, дБмО
Б
a=6,5 дБ
+4, дБмО –13, дБмО
–3.5, дБмО
0, дБмО
106.
Гришин ОПТССОднополосная четырехпроводная система передачи
107.
Гришин ОПТССДвухполосная двухпроводная система передачи
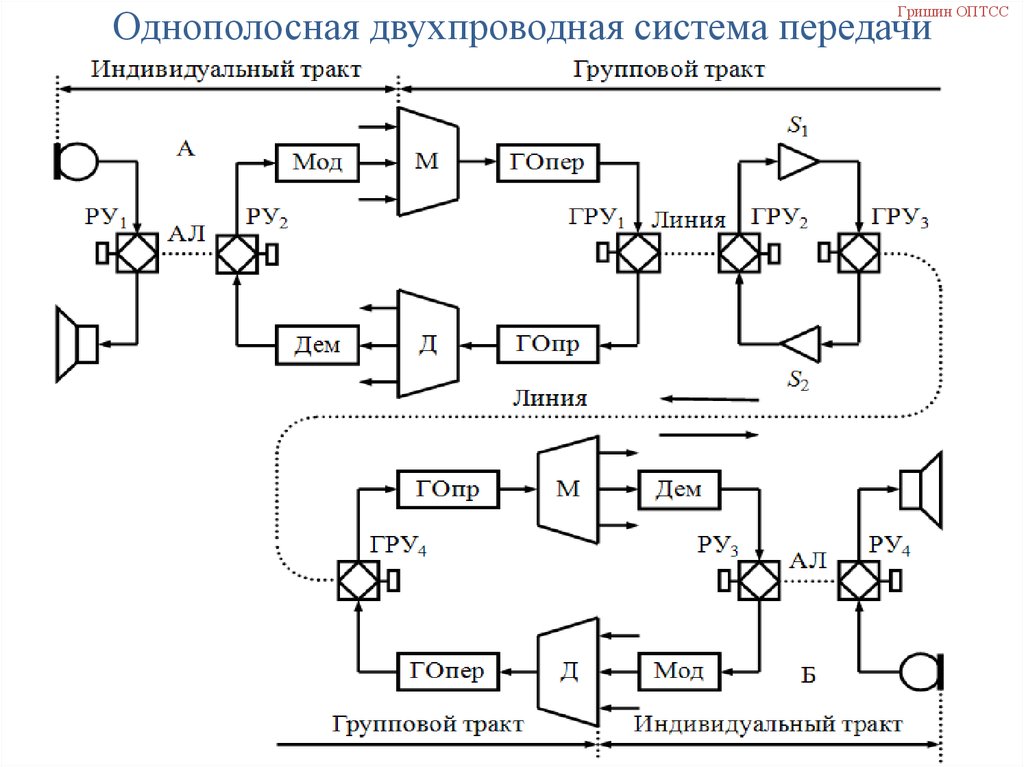
108.
Гришин ОПТССОднополосная двухпроводная система передачи
109.
Методы построения МСП с ЧРК•Индивидуальный и групповой методы построения МСП с
ЧРК
•Каналообразование в МСП с ЧРК
•Способы формирования стандартных групп
•Способы преобразования группового спектра в линейный
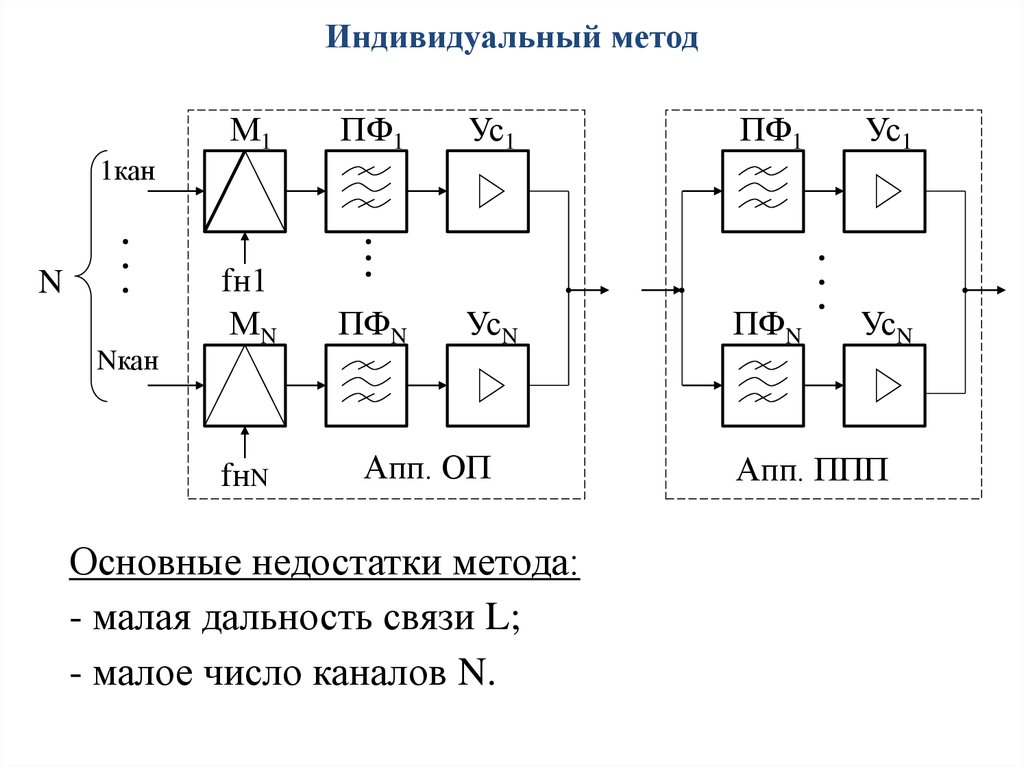
110.
Индивидуальный методМ1
ПФ1
Ус1
ПФ1
Ус1
fн1
МN
ПФN
УсN
ПФN
УсN
1кан
N
Nкан
fнN
Апп. ОП
Основные недостатки метода:
- малая дальность связи L;
- малое число каналов N.
Апп. ППП
111. Методы построения МСП с ЧРК
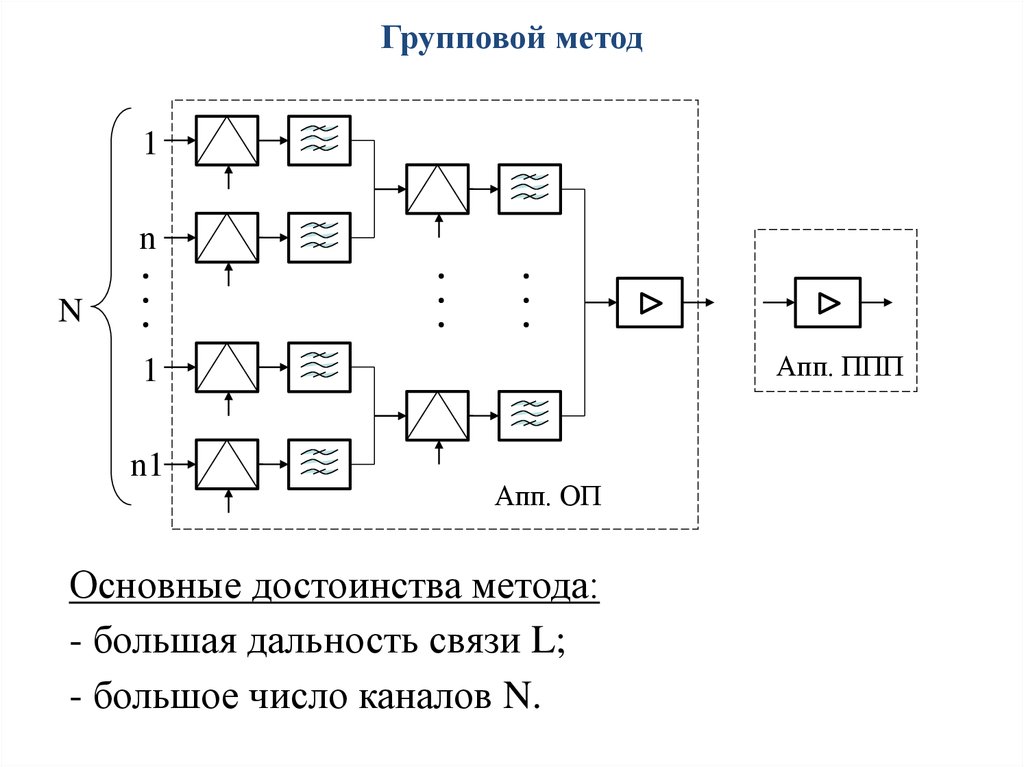
Групповой метод1
n
N
Апп. ППП
1
n1
Апп. ОП
Основные достоинства метода:
- большая дальность связи L;
- большое число каналов N.
112. Индивидуальный метод
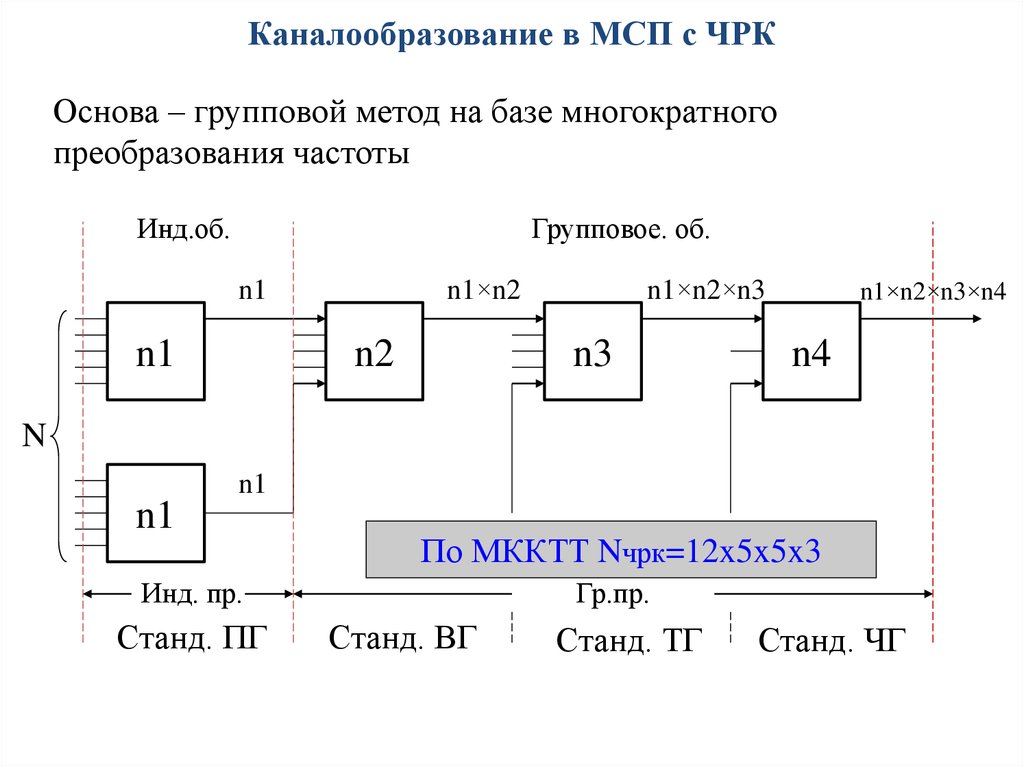
Каналообразование в МСП с ЧРКОснова – групповой метод на базе многократного
преобразования частоты
Инд.об.
Групповое. об.
n1
n1
n1×n2
n2
n1×n2×n3
n3
n1×n2×n3×n4
n4
N
n1
n1
По МККТТ Nчрк=12x5x5x3
Инд. пр.
Станд. ПГ
Гр.пр.
Станд. ВГ
Станд. ТГ
Станд. ЧГ
113. Групповой метод
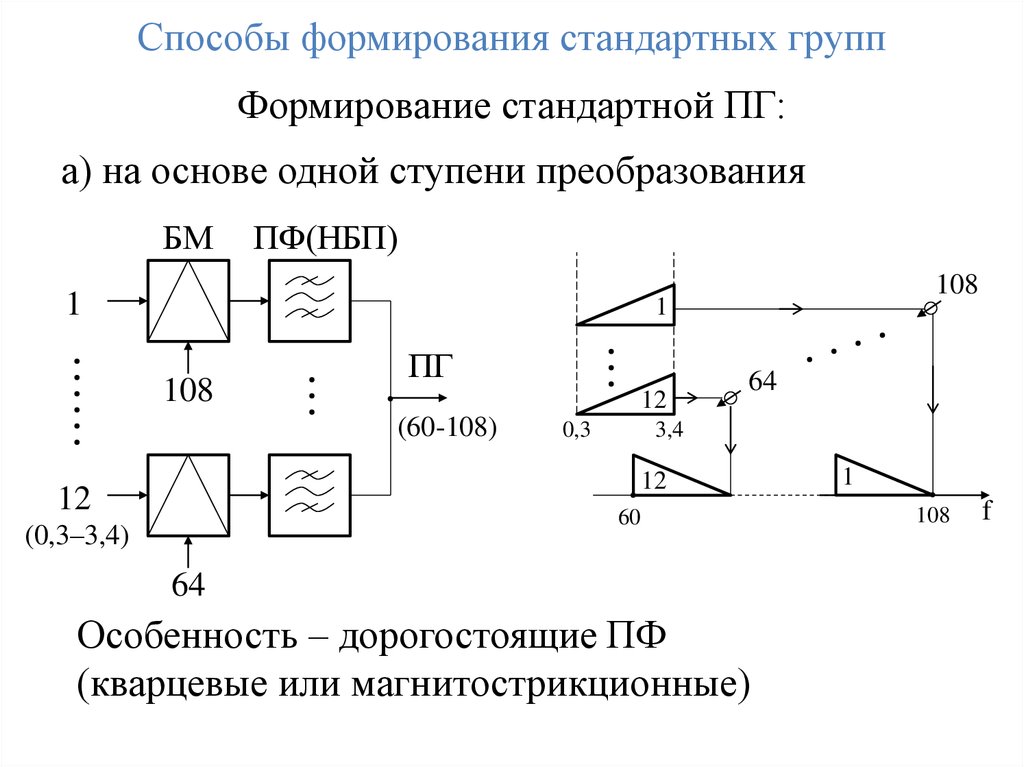
Способы формирования стандартных группФормирование стандартной ПГ:
а) на основе одной ступени преобразования
БМ
ПФ(НБП)
1
108
1
108
ПГ
12
(60-108)
0,3
64
3,4
12
12
60
(0,3–3,4)
64
Особенность – дорогостоящие ПФ
(кварцевые или магнитострикционные)
1
108
f
114. Каналообразование в МСП с ЧРК
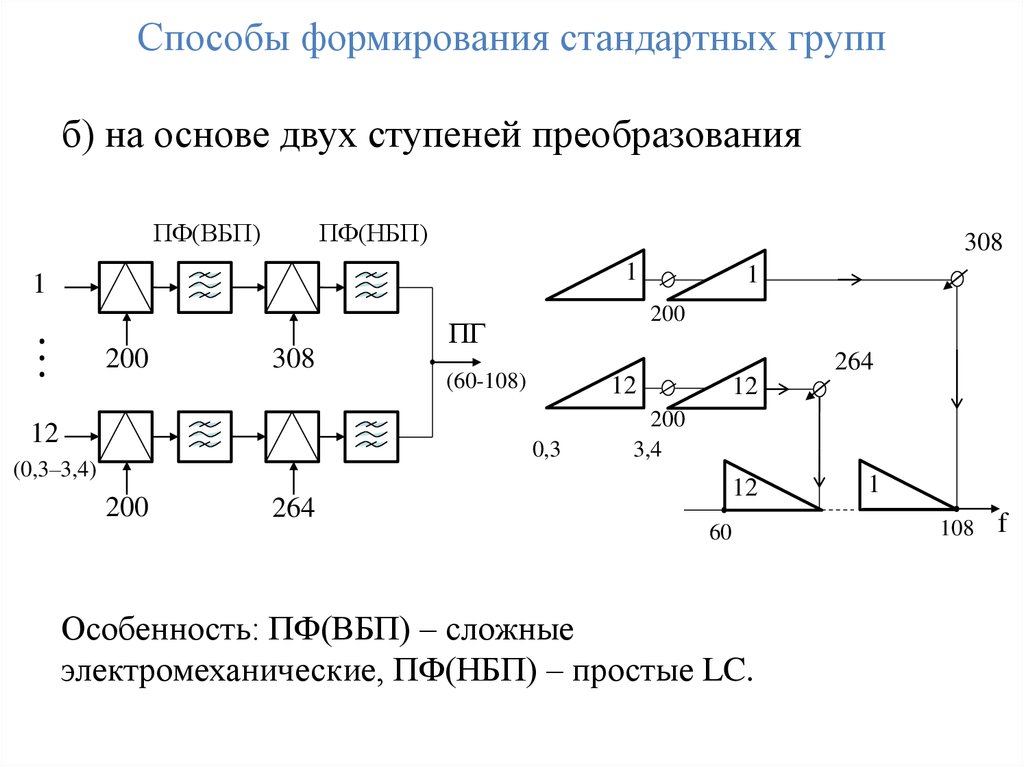
Способы формирования стандартных группб) на основе двух ступеней преобразования
ПФ(ВБП)
ПФ(НБП)
308
1
1
200
308
12
200
ПГ
264
(60-108)
12
0,3
(0,3–3,4)
200
1
12
200
3,4
12
264
60
Особенность: ПФ(ВБП) – сложные
электромеханические, ПФ(НБП) – простые LC.
1
108
f
115. Способы формирования стандартных групп
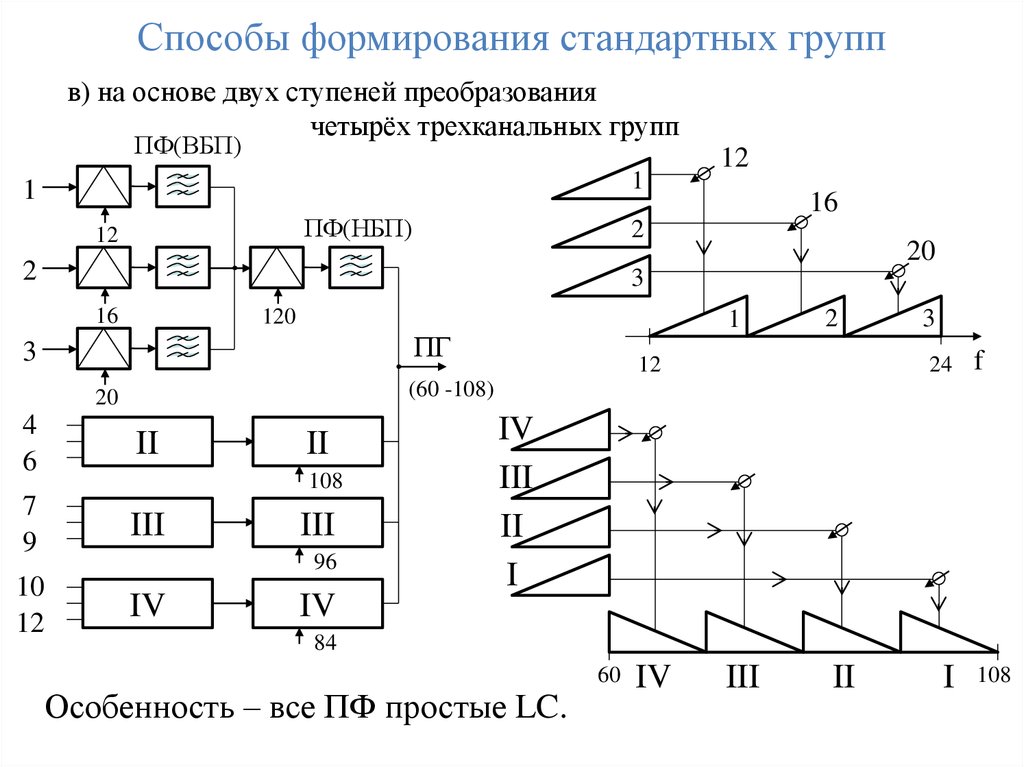
в) на основе двух ступеней преобразованиячетырёх трехканальных групп
ПФ(ВБП)
1
1
ПФ(НБП)
12
12
16
2
2
20
3
16
120
1
ПГ
3
2
12
3
24
f
(60 -108)
20
4
6
II
7
9
III
10
12
IV
II
108
III
96
IV
III
II
I
IV
84
Особенность – все ПФ простые LC.
60
IV
III
II
I
108
116.
Способы формирования стандартных группФормирование стандартной ВГ
ПФ(НБП)
1ПГ
420
ВГ
(312 -552)
5ПГ
612
Основной
420
I
Дополнительный
420
I
564
612
V
I
312
II III IV V
552
252(48)
I
444
V
Инверсный
444
V
I
312
II III IV V
552
Особенность – все ПФ простые LC.
I
312
II III IV V
552
117.
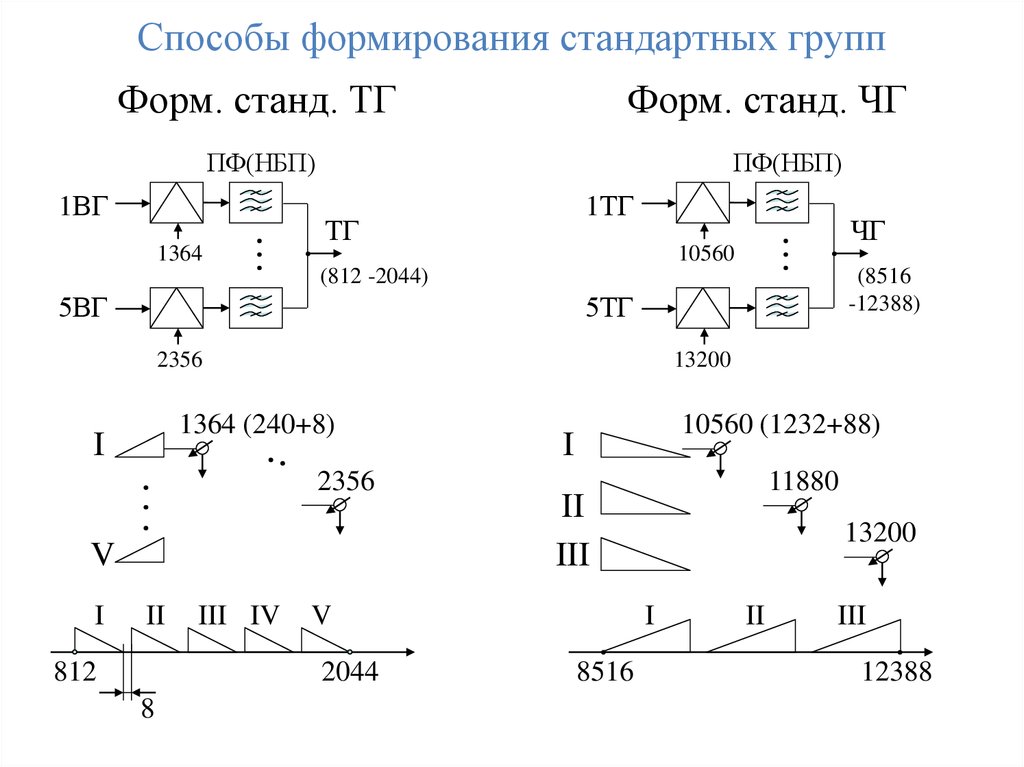
Способы формирования стандартных группФорм. станд. ТГ
Форм. станд. ЧГ
ПФ(НБП)
1ВГ
1364
ПФ(НБП)
1ТГ
ТГ
ЧГ
10560
(812 -2044)
5ВГ
(8516
-12388)
5ТГ
2356
13200
1364 (240+8)
I
2356
V
I
II
812
III IV
I
11880
II
III
V
2044
8
10560 (1232+88)
13200
I
8516
II
III
12388
118. Формирование стандартной ВГ
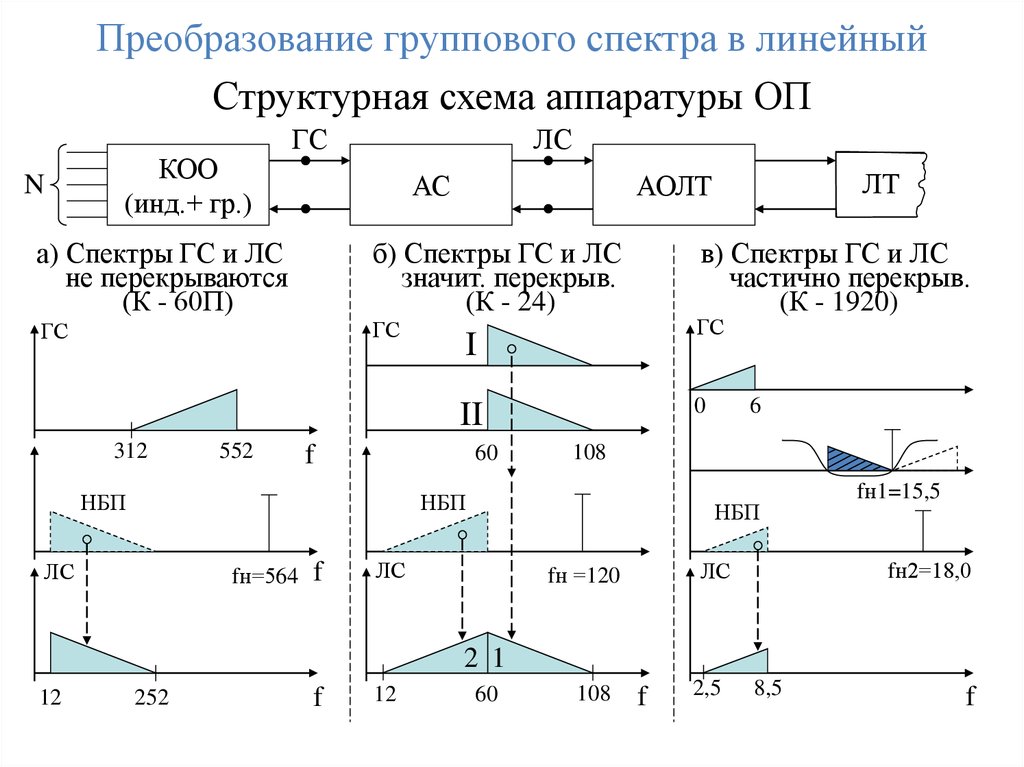
Преобразование группового спектра в линейныйСтруктурная схема аппаратуры ОП
N
КОО
(инд.+ гр.)
ГС
ЛС
АС
а) Спектры ГС и ЛС
не перекрываются
(К - 60П)
б) Спектры ГС и ЛС
значит. перекрыв.
(К - 24)
ГС
ГС
в) Спектры ГС и ЛС
частично перекрыв.
(К - 1920)
ГС
I
0
II
312
552
f
60
НБП
fн=564
f
6
108
НБП
ЛС
ЛТ
АОЛТ
НБП
ЛС
ЛС
fн =120
fн1=15,5
fн2=18,0
2 1
12
252
f
12
60
108
f
2,5
8,5
f
119.
Простейший преобразователь частотыT1
Д1
T2
r
Rг
Efс
E fн Eн max sin( 2 f нt )
E f н E fc
I
I 0
Rг r Rн
1 при E f н 0
(t )
0 при E f н 0
Efн
Rн
Rг
Гришин ОПТСС
EfН<0
EfН>0
E fc Ec max sin( 2 f ct )
I I (t )
1 2
1
1
sin 2 f нt sin 3 2 f нt sin 5 2 f нt
2
3
5
Rн
120. Преобразование группового спектра в линейный
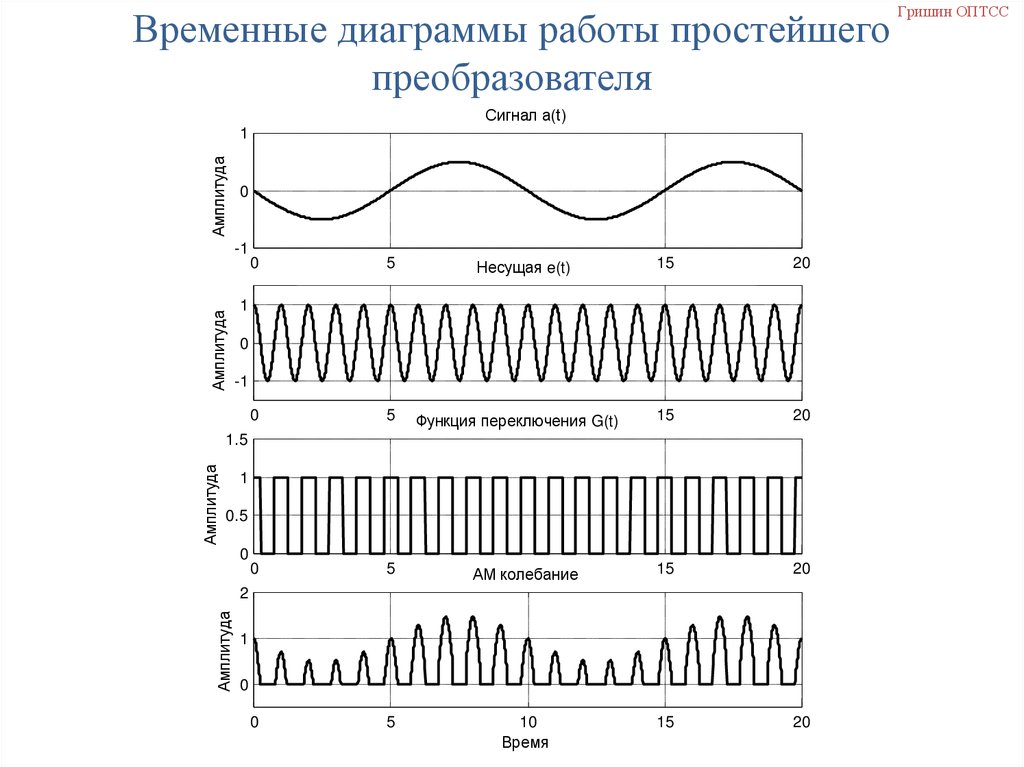
Временные диаграммы работы простейшегопреобразователя
Сигнал a(t)
Амплитуда
1
0
Амплитуда
-1
0
5
0
5
0
5
0
5
15
20
15
20
АМ колебание
15
20
10
Время
15
20
Несущая e(t)
1
0
-1
Функция переключения G(t)
Амплитуда
1.5
1
0.5
0
Амплитуда
2
1
0
Гришин ОПТСС
121.
Гришин ОПТСС2
1
1
1 1
I Eн max sin 2 f нt cos 2 2 f нt cos 4 2 f нt
3
3
2
2
1
1
1
Ec max sin 2 f ct cos 2 f н f c t cos 2 f н f c t
2
1
1
1
cos 2 3 f н f c t cos 2 3 f н f c t
3
3
Rг Rн r
2
U fc 1 U
Rг
Pfc
8Rг
2 2
a 10 lg
Pfc
Pfн fc
2
fc
2
Pf н fc
U fc Rн
U 2fc Rн
1
Rн 2
2
2
R
R
2
R
R
г
н
г
н
Rг Rн
20 lg 20 lg
2 Rг Rн
]R R a 20 lg 10, дБ
н
min
г
122.
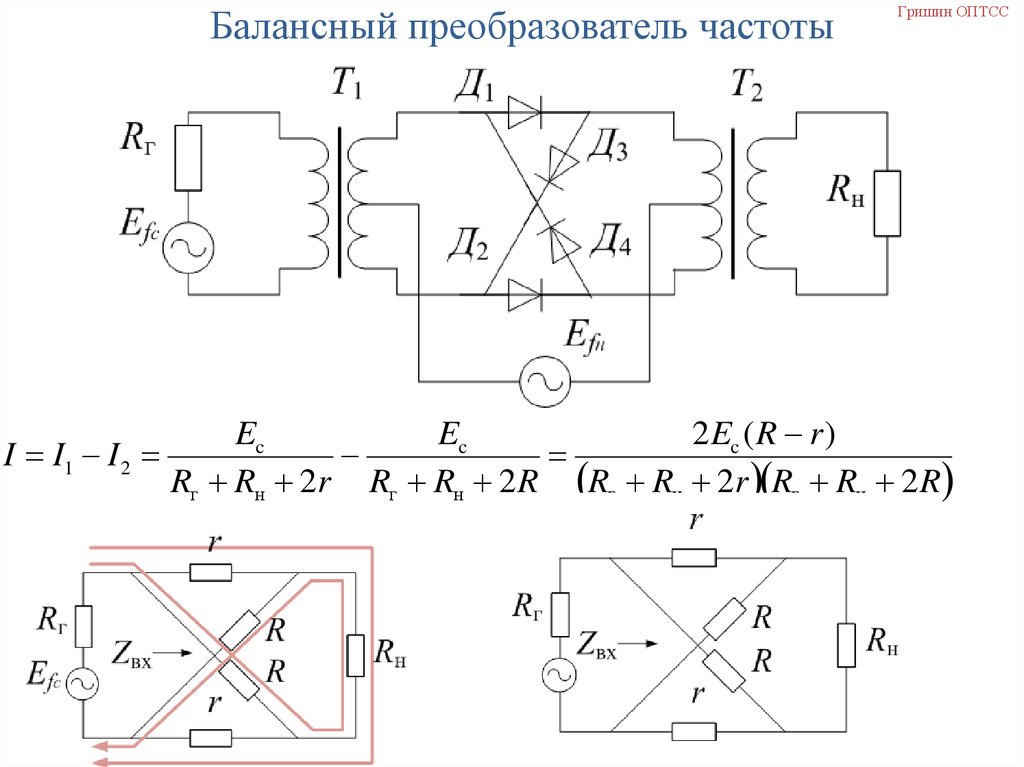
Балансный преобразователь частотыГришин ОПТСС
1
1
1
I Ec max sin 2 f ct cos 2 f н f c t cos 2 f н f c t
2
1
1
1
cos 2 3 f н f c t cos 2 3 f н f c t
3
3
Rг Rн r
Rг Rн 2r Rг Rн 2 R
a 20 lg 20 lg
4
R
r
R
R
г н
k 1
R
, k
a 20 lg 20 lg
r
k
1
123.
Гришин ОПТССВременные и спектральные диаграммы работы балансного
преобразователя частоты
Амплитуда
Амплитуда
Сигнал a(t)
1
0
-1
5 Функция переключения G(t) 15
20
0
5
АМ колебание
15
20
0
5
10
Время
15
20
1.5
1
0.5
0
-0.5
Амплитуда
0
1
0
-1
124.
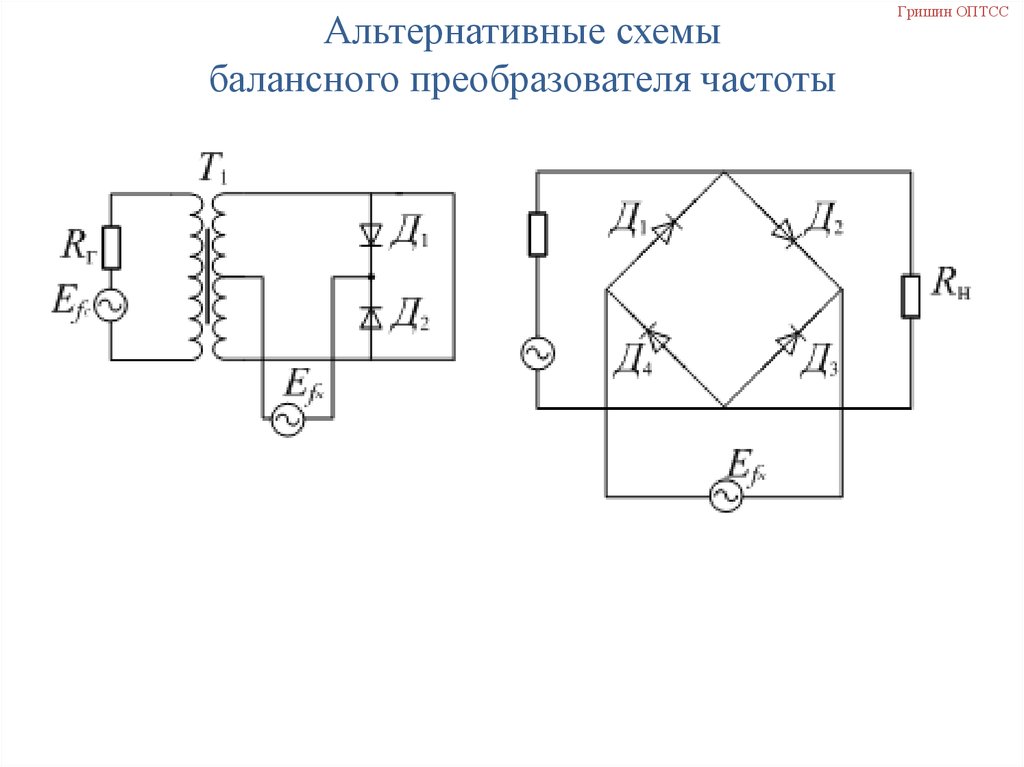
Альтернативные схемыбалансного преобразователя частоты
Гришин ОПТСС
125. Временные и спектральные диаграммы работы балансного преобразователя частоты
Балансный преобразователь частотыI I1 I 2
Гришин ОПТСС
Ec
Ec
2 Ec ( R r )
Rг Rн 2r Rг Rн 2 R Rг Rн 2r Rг Rн 2 R
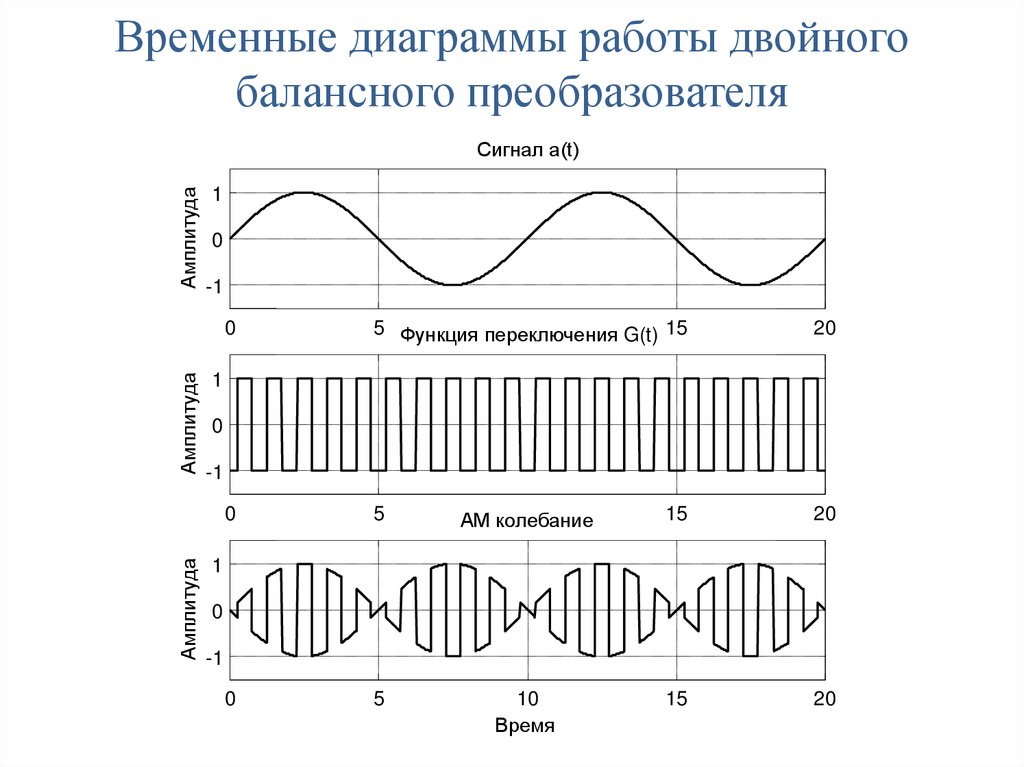
126.
Временные диаграммы работы двойногобалансного преобразователя
Амплитуда
Амплитуда
Амплитуда
Сигнал a(t)
1
0
-1
0
5 Функция переключения G(t) 15
20
0
5
АМ колебание
15
20
0
5
10
Время
15
20
1
0
-1
1
0
-1
127.
41
1
sin 2 f нt sin 3 2 f нt sin 5 2 f нt
3
5
1 при E f н 0
(t )
1 при E f н 0
I
4
Ec max ( R r )
Rг Rн 2r Rг Rн 2 R
1
1
cos 2 (nfн f с )t cos 2 (nfн f с )t , n 1, 3, 5...
n 1 n
n 1 n

































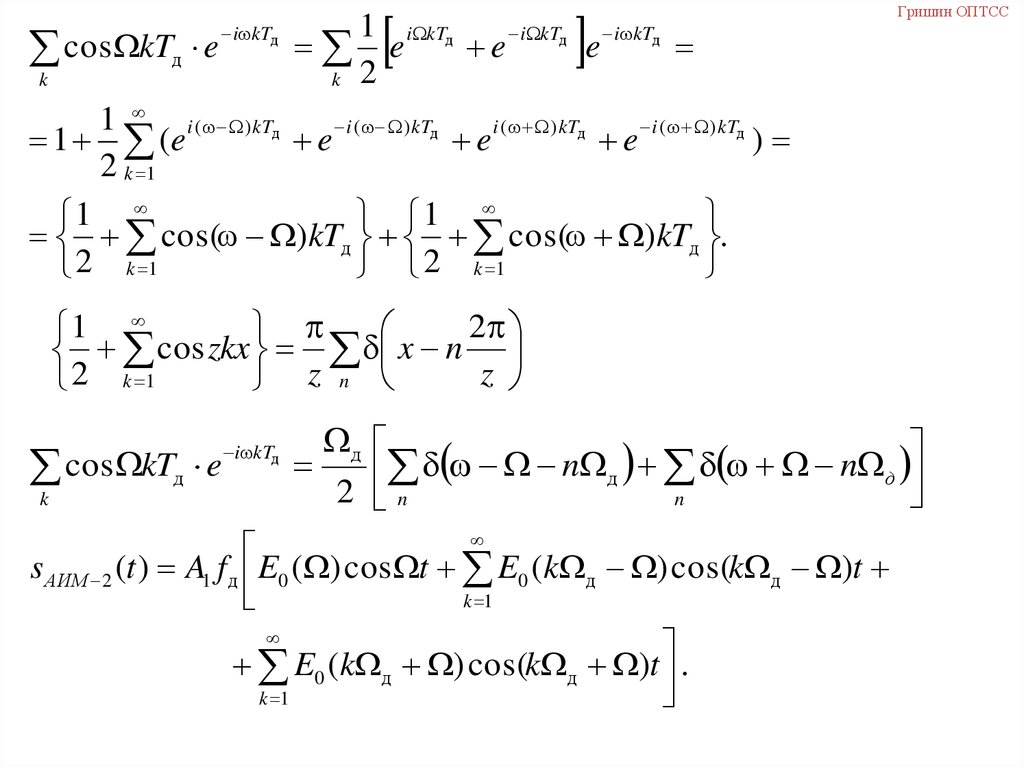
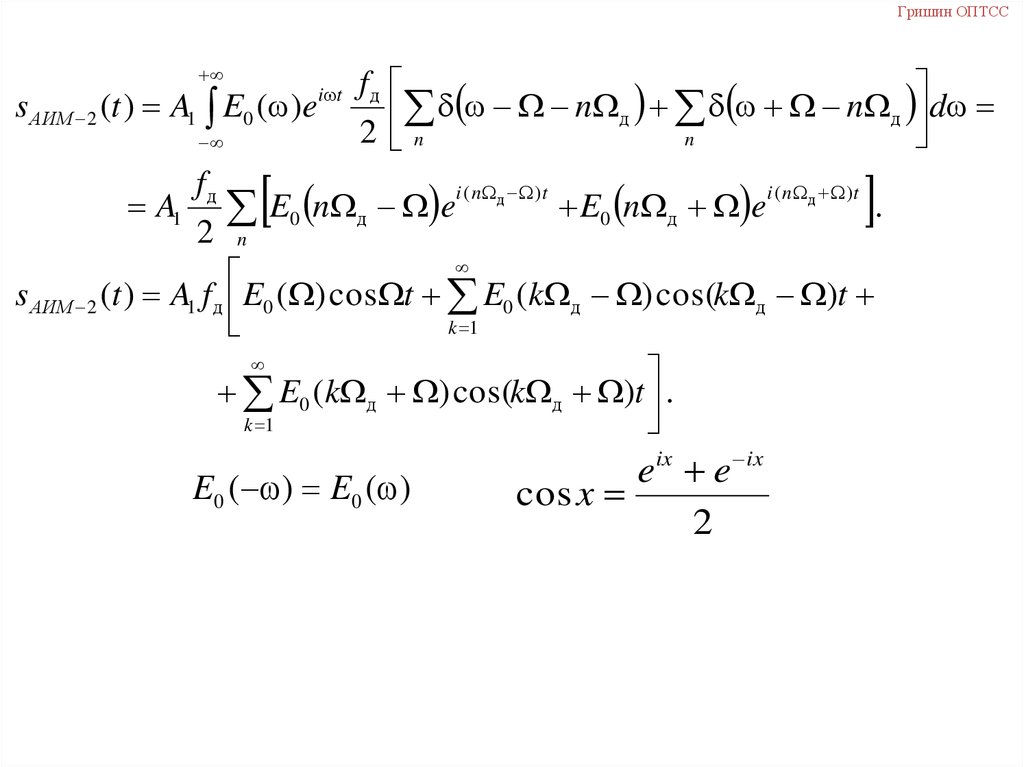


































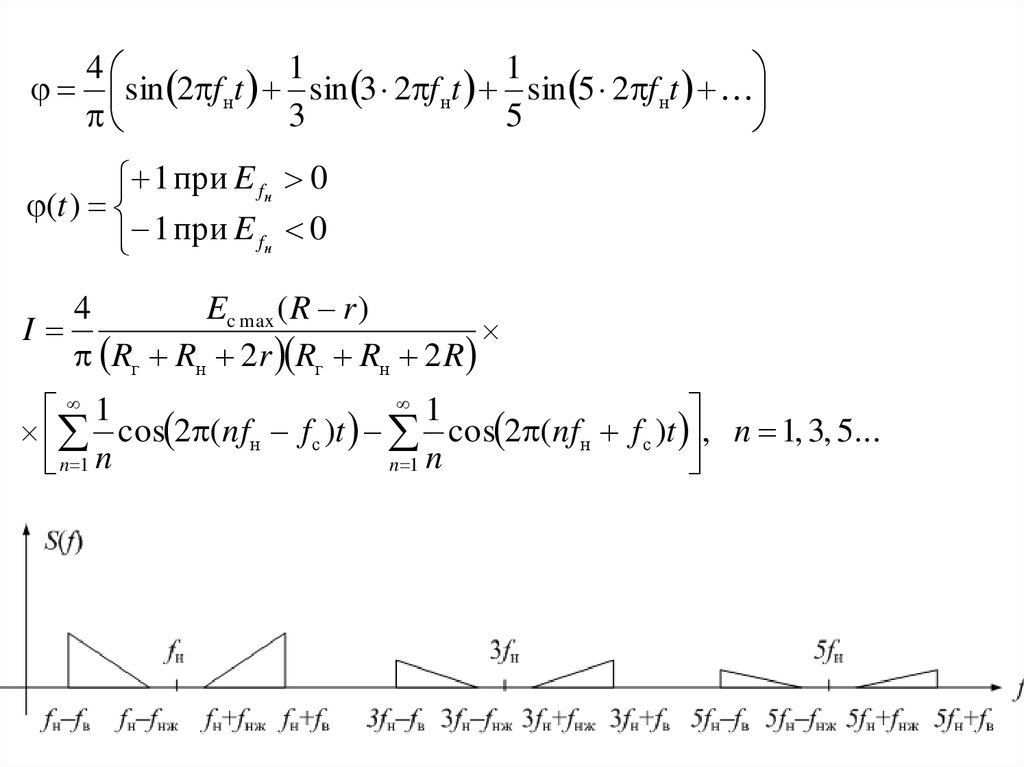
 Физика
Физика








