Stochastic Modeling. Discrete RV

1.

Simulation
STOCHASTIC MODELING

2.

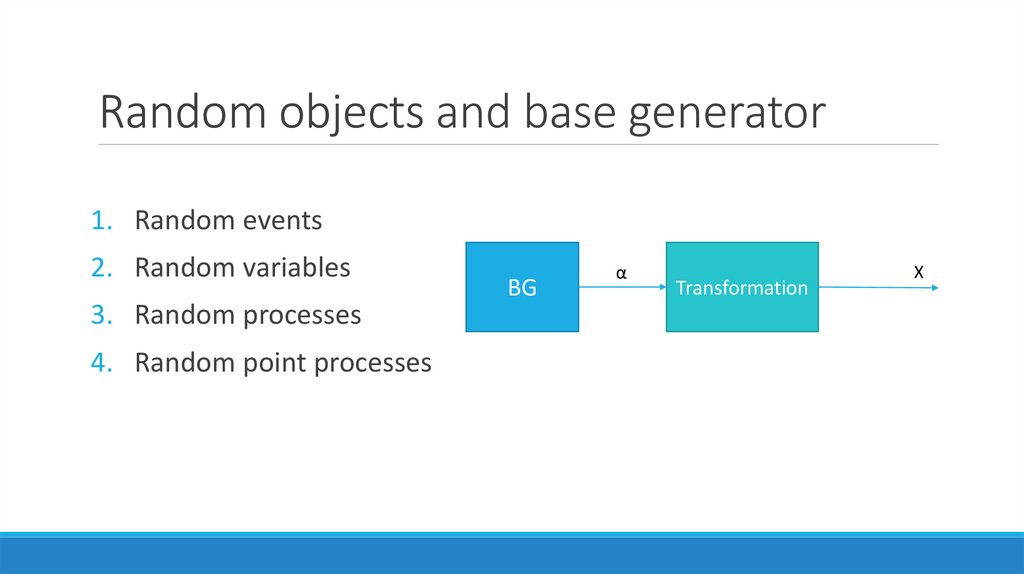
Random objects and base generator
1. Random events
2. Random variables
3. Random processes
4. Random point processes
BG
α
Transformation
X

3.

Discrete RV
METHODS OF GENERATION

4.

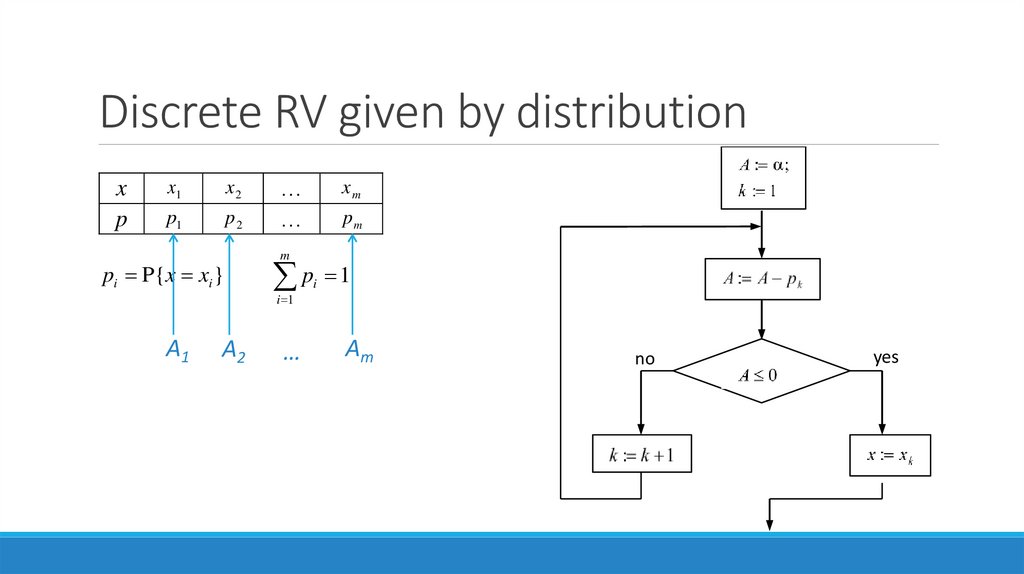
Discrete RV given by distribution
x
p
x1
x2
p1
p2
pi P{x xi }
…
…
A2
pm
m
p 1
i 1
A1
xm
…
i
Am
no
yes

5.

Statistical processing
for discrete RVs
x
p
x1
x2
p1
p2
…
…
xm
Relative frequencies
pˆ i
ni
N
ni is the number of appearances of value i
(they are named as frequencies),
N is the total number of trials
Empiric expectation (average):
pm
m
Eˆ x pˆ i xi
i 1
m
Mathematical expectation (mean):
E x pi xi
Empiric variance:
m
ˆ x
D
pˆ x 2 (Eˆ x)2
i 1
i 1
m
m
i 1
i 1
Variance: Var x D x pi ( xi E x) 2 pi xi2 (E x) 2
Absolute errors:
i i
E Ê x E x
D D̂ x D x
Relative errors:
E
E
Ex
D
D
Dx

6.

Statistical processing
for discrete RVs
Chi-squared test
m
2
n
i
Xˆ
N
i 1 Npi
m
2
N
Hypothesis that empiric distribution corresponds to the
theoretical one is not true if and only if
Xˆ N2 12 ,m 1
α is a significance level
m

7.

Laboratory #9
ASSIGNMENT:
Simulation of discrete random variable
• Implement an algorithm for conducting a series of experiments to simulate a discrete random
variable specified by the distribution
• Calculate empirical probabilities, sample mean and variance, their relative errors
• Calculate the chi-squared statistic and apply the chi-squared test for different values of N (N =
10, 100, 1,000, 10,000)
• Draw a conclusion

8.

Laboratory #9
ЗАДАНИЕ:
Имитационное моделирование дискретных случайных величин
• Реализовать алгоритм проведения серии экспериментов по генерации
дискретной случайной величины, заданной рядом распределения
• Вычислить эмпирические вероятности, выборочные среднее и дисперсию, их
относительные погрешности
• Вычисление статистику хи-квадрат и применить критерий хи-квадрат при разных
значениях N (N = 10, 100, 1 000, 10 000)
• Сделать вывод

9.

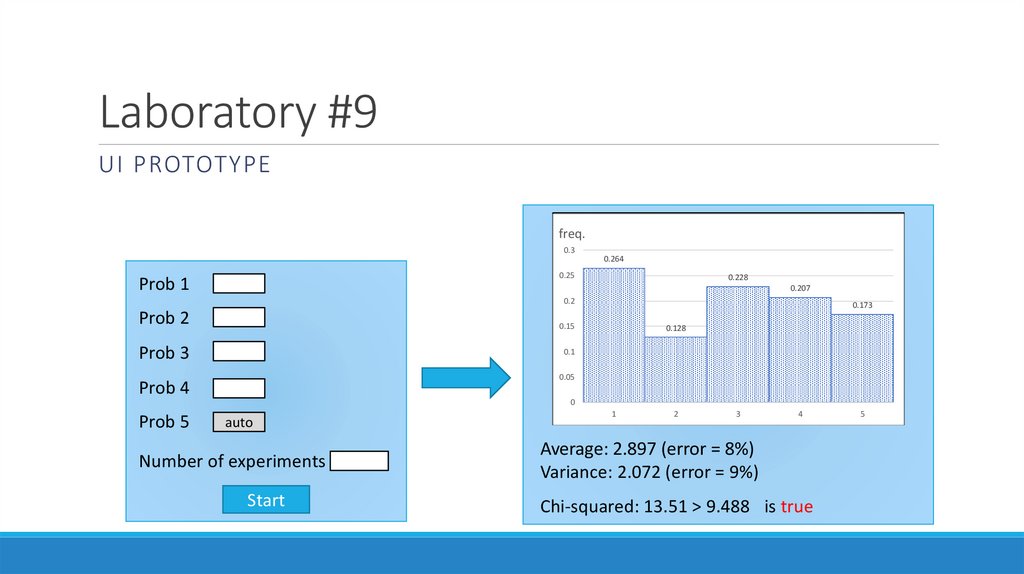
Laboratory #9
UI PROTOTYPE
freq.
0.3
0.264
0.25
Prob 1
0.228
0.207
0.2
Prob 2
0.15
Prob 3
0.128
0.1
0.05
Prob 4
Prob 5
0.173
0
auto
Number of experiments
Start
1
2
3
4
Average: 2.897 (error = 8%)
Variance: 2.072 (error = 9%)
Chi-squared: 13.51 > 9.488 is true
5

10.

Uniform discrete distribution
FROM 0 TO n:
x
p
0
1
1
n 1
1
n 1
FROM a TO b:
…
…
n
1
n 1
GENERATOR:
x Int( (n 1))
Int is a truncating operation
1.
Set n = b - a
2.
Use
3.
Calculate x = x + a
For example, if x from {1, 2, .., n} then use formula:
x Int( (n 1))
x Int( n) 1

11.

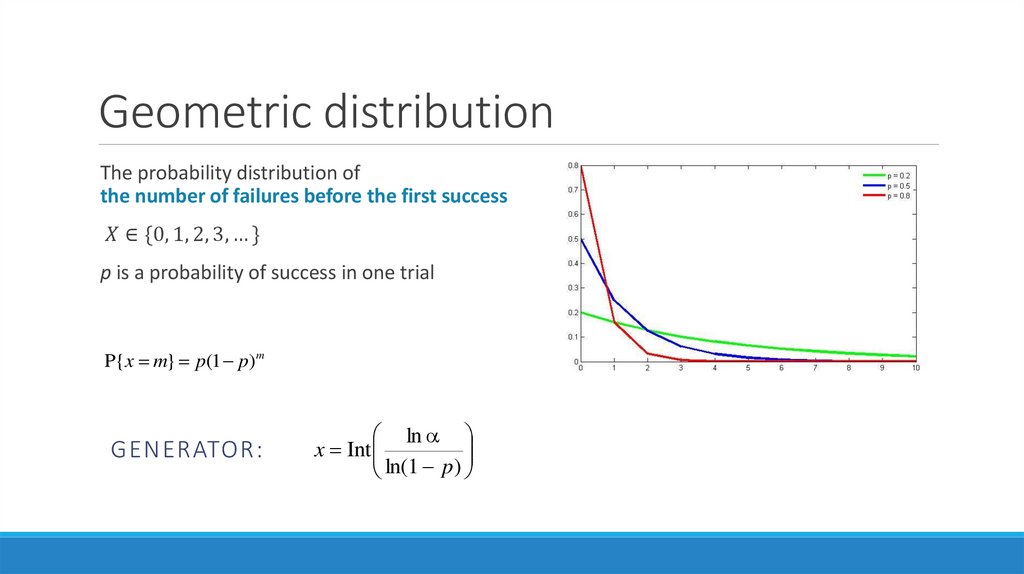
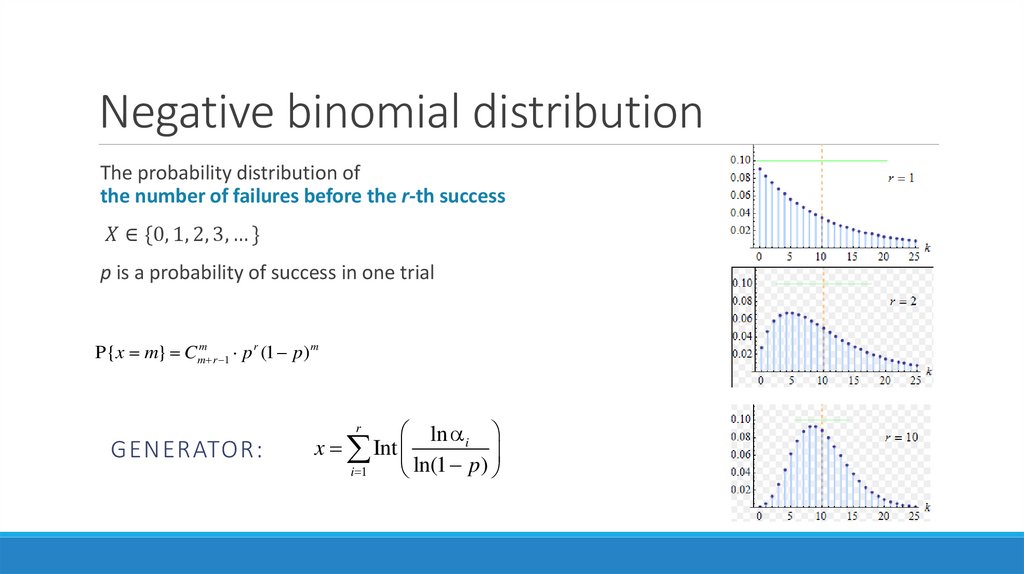
Geometric distribution
The probability distribution of
the number of failures before the first success