Похожие презентации:
Стохастическое моделирование. Моделирование дискретных случайных величин
1.
Стохастическоемоделирование
МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
2.
Случайные объекты и базовый датчик1. Случайные события
2. Случайные величины
3. Случайные процессы
4. Случайные потоки событий
БД
α
Преобразование
X
3.
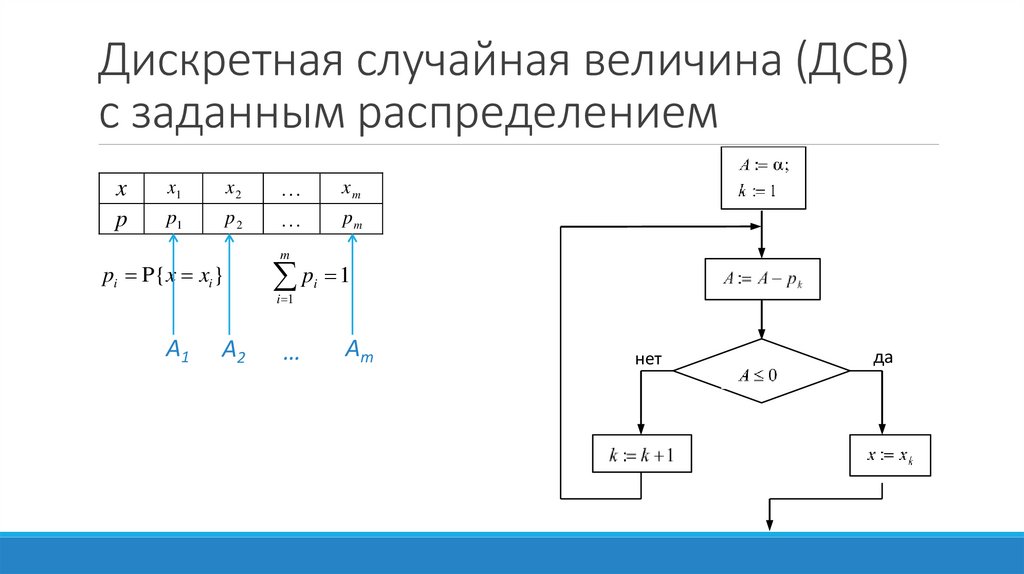
Дискретная случайная величина (ДСВ)с заданным распределением
x
p
x1
x2
p1
p2
pi P{x xi }
…
…
A2
pm
m
p 1
i 1
A1
xm
…
i
Am
нет
да
4.
Относительные частотыn
Статистическая обработка
эмпирический ряд распределения
pˆ
N
результатов для ДСВ
n – частота значения x (сколько раз наблюдалось
i
i
i
x
p
x1
x2
p1
p2
…
…
xm
m
E x pi xi
i 1
m
m
Var x D x pi ( xi E x) pi xi2 (E x) 2
2
i 1
это значение),
N – объем выборки (общее число испытаний)
pm
Математическое ожидание (среднее):
Дисперсия:
i
i 1
(Эмпирическое) среднее:
m
Eˆ x
pˆ x
i 1
i
i
Эмпирическая дисперсия:
m
ˆ x
D
pˆ x 2 (Eˆ x)2
i 1
i i
Абсолютные погрешности:
E Ê x E x
D D̂ x D x
Относительные погрешности:
E
E
Ex
D
D
Dx
5.
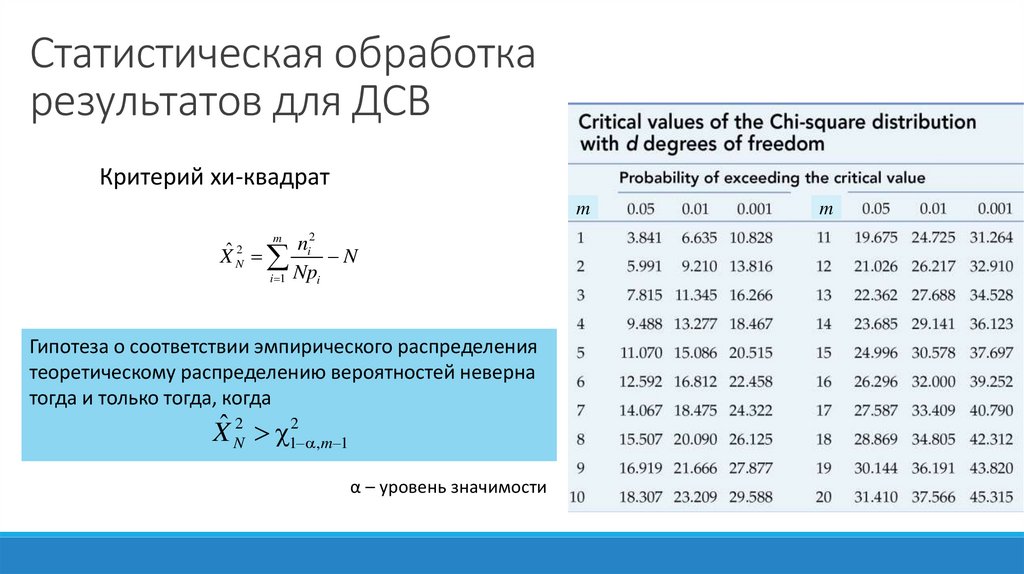
Статистическая обработкарезультатов для ДСВ
Критерий хи-квадрат
m
2
n
Xˆ i N
i 1 Npi
m
2
N
Гипотеза о соответствии эмпирического распределения
теоретическому распределению вероятностей неверна
тогда и только тогда, когда
Xˆ N2 12 ,m 1
α – уровень значимости
m
6.
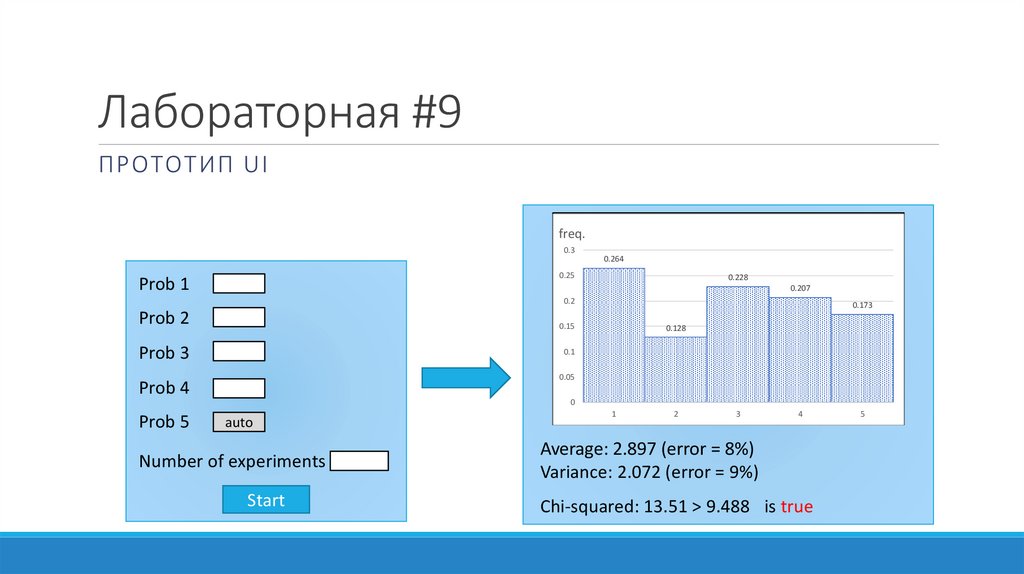
Лабораторная 9ЗАДАНИЕ:
Имитационное моделирование дискретных случайных величин
• Реализовать алгоритм проведения серии экспериментов по генерации
дискретной случайной величины, заданной рядом распределения
• Вычислить эмпирические вероятности, выборочные среднее и дисперсию, их
относительные погрешности
• Вычисление статистику хи-квадрат и применить критерий хи-квадрат при разных
значениях N (N = 10, 100, 1 000, 10 000)
• Сделать вывод
7.
Лабораторная #9ПРОТОТИП UI
freq.
0.3
0.264
0.25
Prob 1
0.228
0.207
0.2
Prob 2
0.15
Prob 3
0.128
0.1
0.05
Prob 4
Prob 5
0.173
0
auto
Number of experiments
Start
1
2
3
4
Average: 2.897 (error = 8%)
Variance: 2.072 (error = 9%)
Chi-squared: 13.51 > 9.488 is true
5
8.
Моделированиедискретных случайных
величин
СПЕЦИАЛЬНЫЕ МЕТОДЫ
9.
Равномерное дискретноераспределение
ОТ 0 ДО n:
x
p
0
1
1
n 1
1
n 1
ОТ a ДО b:
…
…
n
1
n 1
ДАТЧИК:
x Int( (n 1))
Int – целая часть (без округления)
1.
n=b-a
2.
x Int( (n 1))
3.
x=x+a
Например, для x из {1, 2, .., n} используется формула: x Int( n) 1
10.
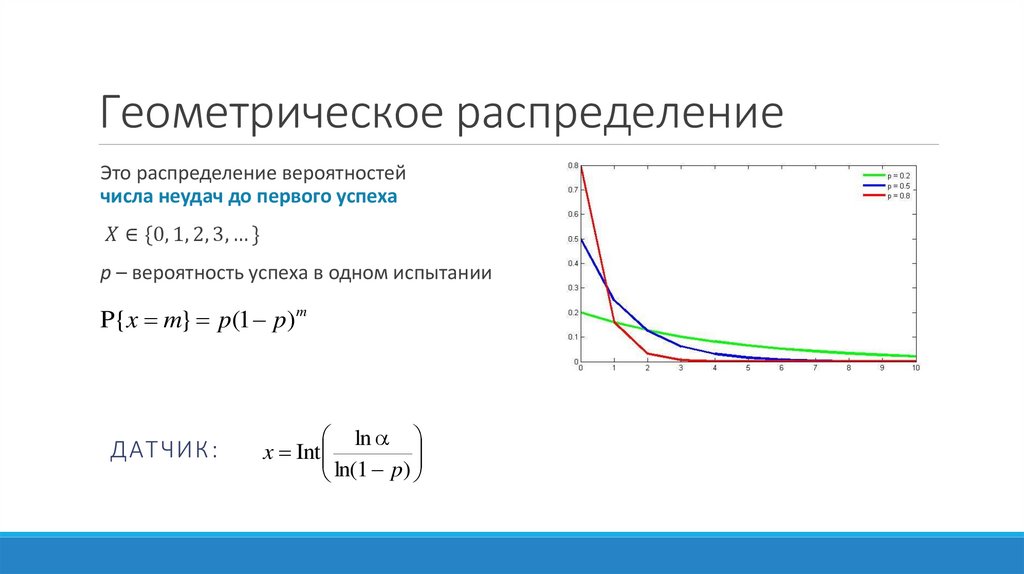
Геометрическое распределениеЭто распределение вероятностей
числа неудач до первого успеха







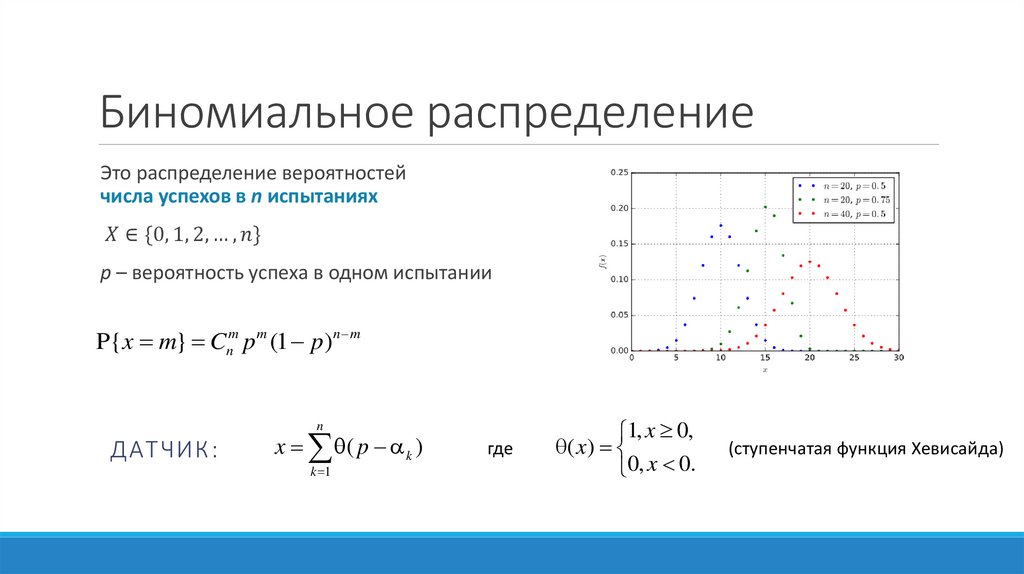

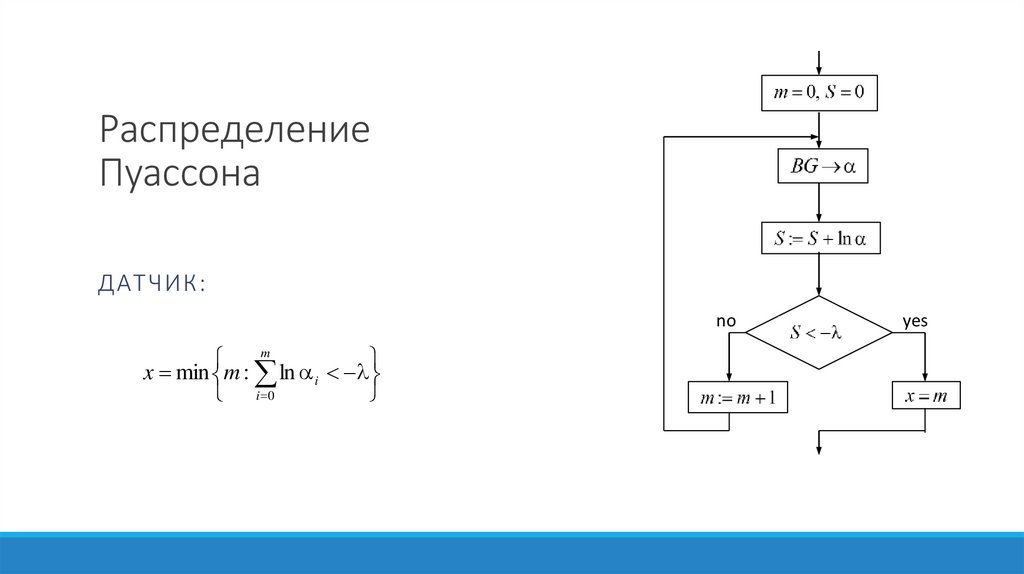



 Математика
Математика








