Стохастическое моделирование. Моделирование случайных событий

1.

Стохастическое
моделирование
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ

2.

Случайные объекты и базовый датчик
1. Случайные события
2. Случайные величины
3. Случайные процессы
4. Случайные потоки событий
БД
α
Преобразование
X

3.

Геометрический смысл вероятности
random
0
p
P{random < p} = p
1

4.

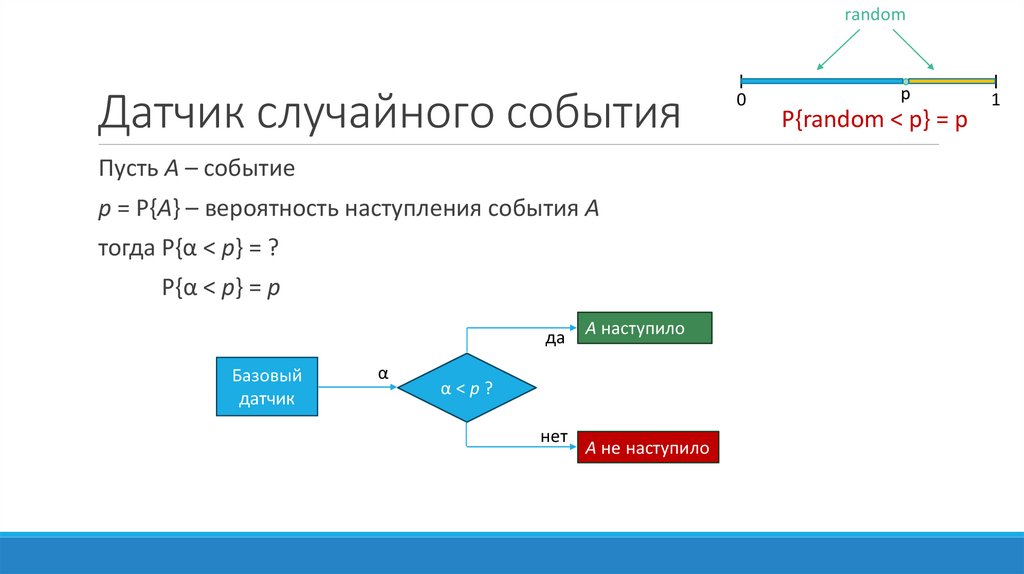
random
Датчик случайного события
Пусть A – событие
p = P{A} – вероятность наступления события А
тогда P{α < p} = ?
P{α < p} = p
да
Базовый
датчик
α
А наступило
α<p?
нет
А не наступило
0
p
P{random < p} = p
1

5.

Лабораторная 8.1
ЗАДАНИЕ:
• Приложение “Скажи ‘да’ или ‘нет’”
Пойти сегодня в университет?
ответ
НЕТ!

6.

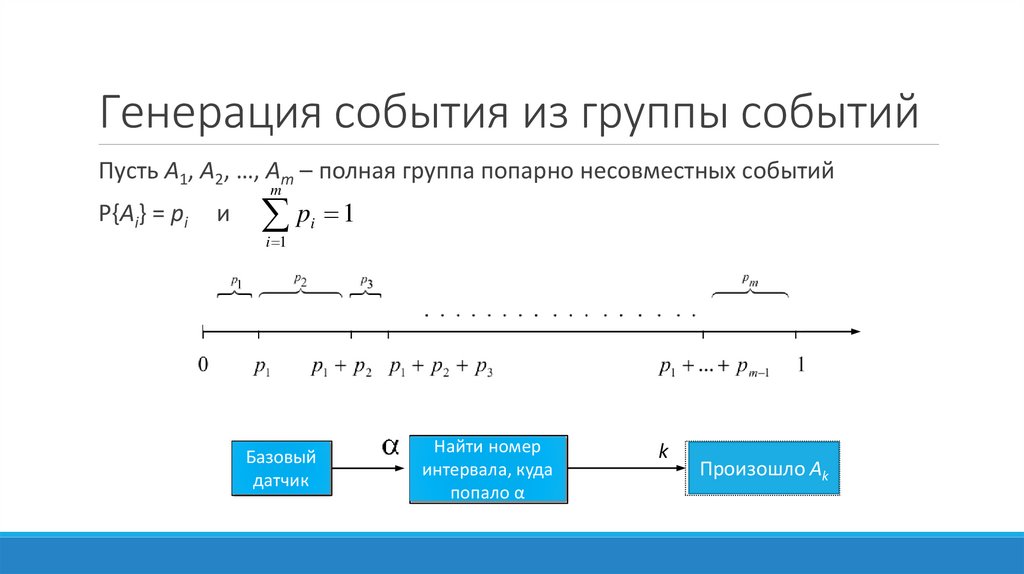
Генерация события из группы событий
Пусть A1, A2, …, Am – полная группа попарно несовместных событий
m
P{Ai} = pi
и
p 1
i 1
i
Базовый
датчик
Найти номер
интервала, куда
попало α
k
Произошло Ak

7.

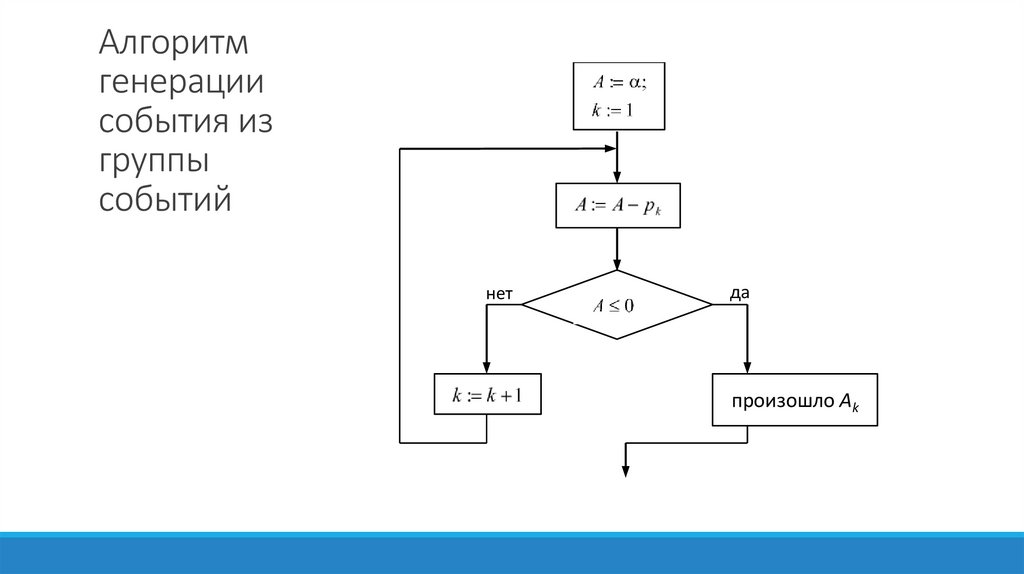
Алгоритм
генерации
события из
группы
событий
нет
да
произошло Ak

8.

Лабораторная 8.2
ЗАДАНИЕ:
• “Шар предсказаний” (“Magic 8-Ball”)

9.

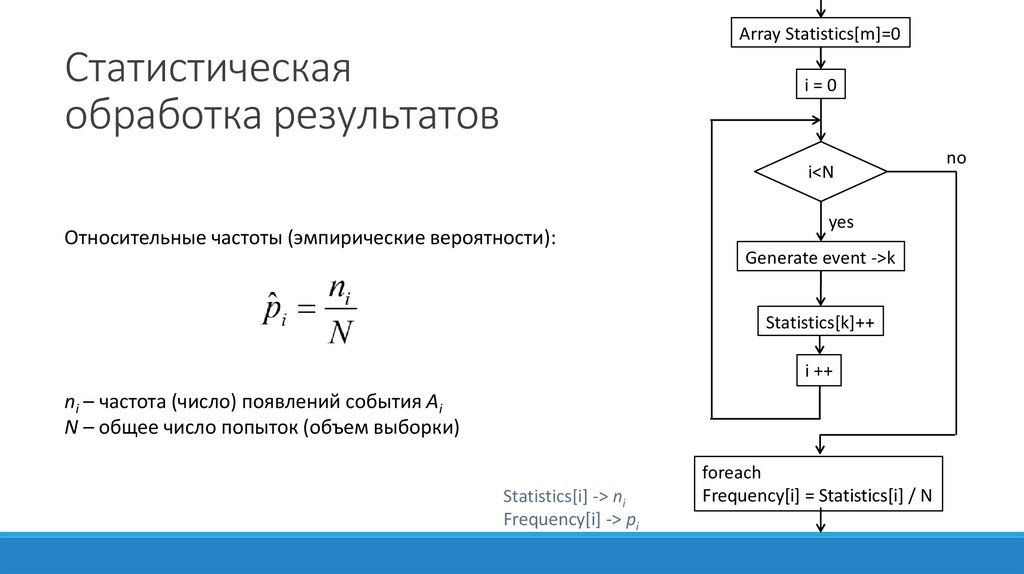
Array Statistics[m]=0
Статистическая
обработка результатов
i=0
i<N
Относительные частоты (эмпирические вероятности):
yes
Generate event ->k
Statistics[k]++
i ++
ni – частота (число) появлений события Ai
N – общее число попыток (объем выборки)
Statistics[i] -> ni
Frequency[i] -> pi
foreach
Frequency[i] = Statistics[i] / N
no

10.

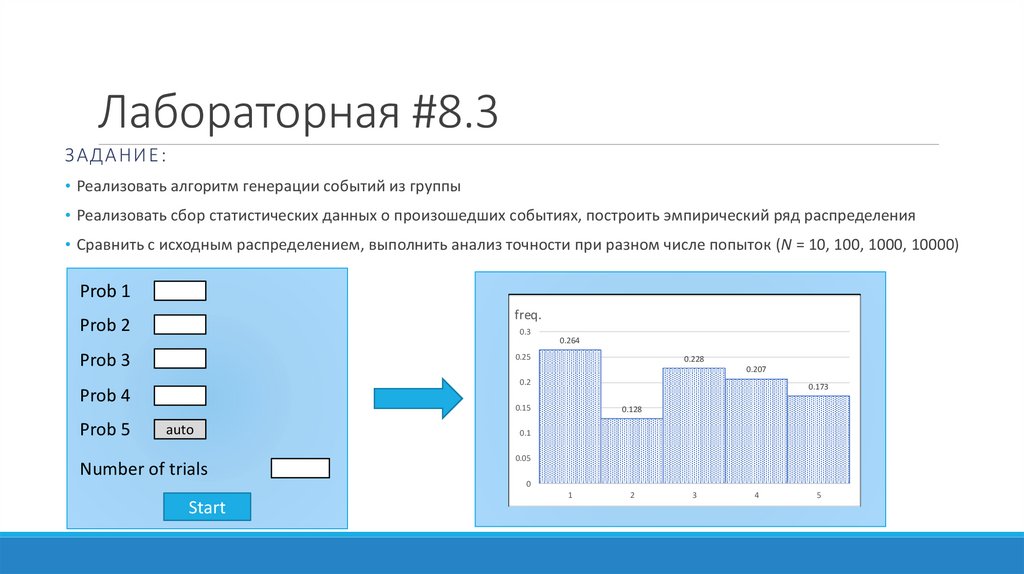
Лабораторная #8.3
ЗАДАНИЕ:
• Реализовать алгоритм генерации событий из группы
• Реализовать сбор статистических данных о произошедших событиях, построить эмпирический ряд распределения
• Сравнить с исходным распределением, выполнить анализ точности при разном числе попыток (N = 10, 100, 1000, 10000)
Prob 1
freq.
Prob 2
0.3
0.264
Prob 3
0.25
0.207
0.2
Prob 4
Prob 5
0.228
0.173
0.15
auto
Number of trials
0.128
0.1
0.05
0
Start
1
2
3
4
5

11.

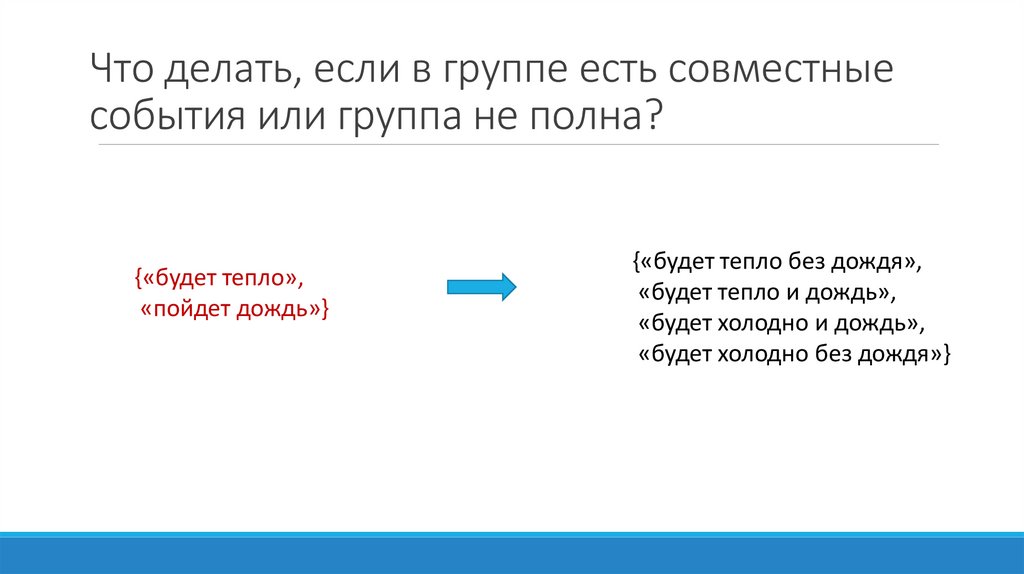
Что делать, если в группе есть совместные
события или группа не полна?
{«будет тепло»,
«пойдет дождь»}
{«будет тепло без дождя»,
«будет тепло и дождь»,
«будет холодно и дождь»,
«будет холодно без дождя»}