Силы в механике. Сила тяжести

1. СИЛЫ В МЕХАНИКЕ.

2. Сила тяжести.

Вблизи поверхности
Земли все тела
падают с одинаковым
ускорением, которое
называют ускорением
свободного падения.
В системе отсчета
связанной с Землей
на всякое тело
действует сила
тяжести.

3. Земля совершает сложное движение:

-

4. Скорости вращения Земли:

вокруг своей оси с угловой скоростью:
2
2
2
5 рад
1
7,27 10
1сут 24часа 24 60 60с
с
вокруг Солнца с угловой скоростью:
2
2
2
1год 365,5 24 60 60с
7 рад
2,02 10
с

5.

Сила тяжести.

6. Сила тяжести определим как геометрическую сумму силы гравитационного притяжения Земли и центробежной силы инерции, учитывающая

эффект
суточного вращения Земли.
Fтяж Fвт Fин

7. Ускорение свободного падения:

• зависит так же от
высоты, измеряемой
от поверхности
Земли. При подъеме
на высоту 300 км
ускорение
свободного падения
уменьшается на
1 м/с2.
M зm
Fв т G
2
Rз h

8. Зависимость ускорения силы тяжести от широты:

2
Fин mr mRз cos
, где
T
T 24часа 86400с
2

9.

• Ускорение свободного падения
измеренное относительно поверхности
Земли у полюсов, равно примерно
9,83 м/с2, на экваторе – 9,78 м/с2, а на
широте 450 – 9,81 м/с2.

10. Вес тела.

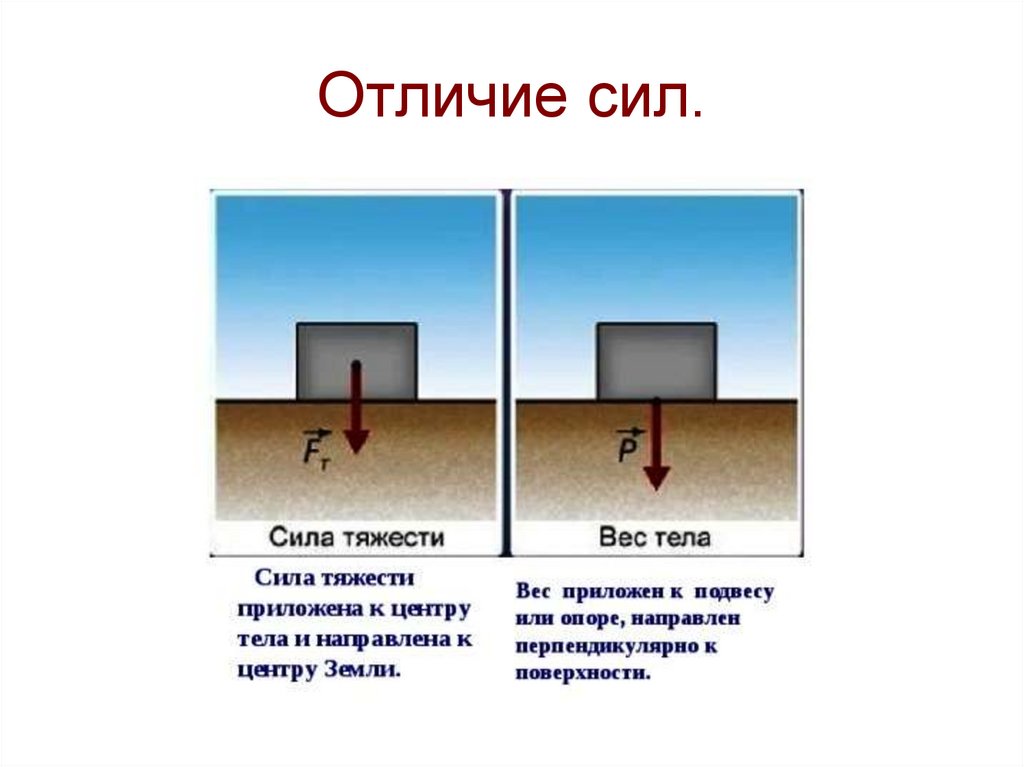
Весом тела
называют силу, с
которой тело
вследствие его
притяжения к Земле
действует на опору
или подвес.

11. Вес тела и сила тяжести.

Согласно третьему закону Ньютона должно
выполняться соотношение
FT P
Таким образом, вес и сила тяжести равны
друг к другу, однако приложены они к
разным телам – вес к подвесу, сила тяжести
– к самому телу.

12. Отличие сил.

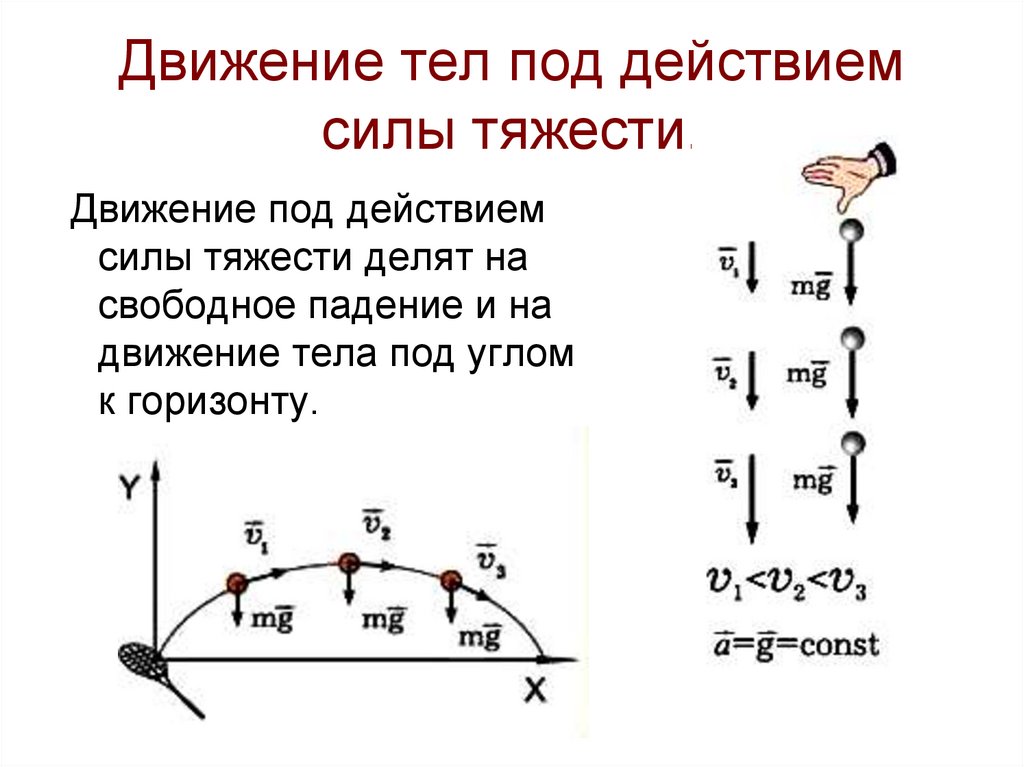
13. Движение тел под действием силы тяжести.

Движение под действием
силы тяжести делят на
свободное падение и на
движение тела под углом
к горизонту.

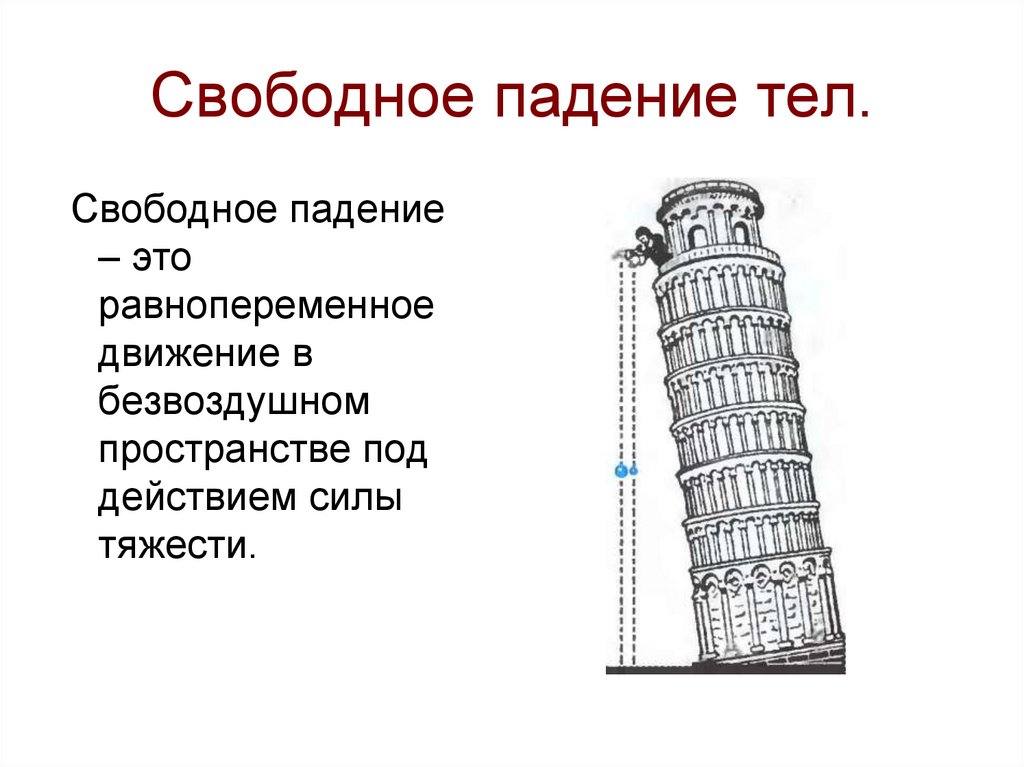
14. Свободное падение тел.

Свободное падение
– это
равнопеременное
движение в
безвоздушном
пространстве под
действием силы
тяжести.

15. Зависимость между кинематическими характеристиками при свободном падении имеют вид:

2
gt
h
, gt
2
0 0

16.

g
t h
g
2 g
h
t
2
2
2g
2h
2h
g
g
g
2hg

17. Движение под углом к горизонту.

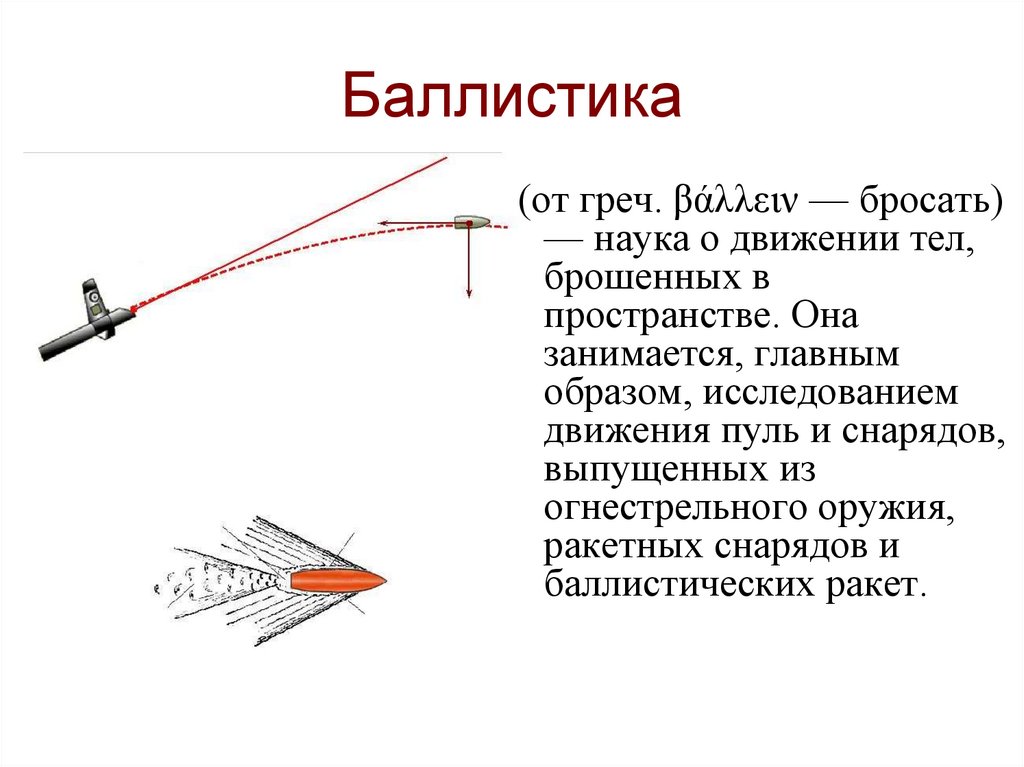
18. Баллистика

(от греч. βάλλειν — бросать)
— наука о движении тел,
брошенных в
пространстве. Она
занимается, главным
образом, исследованием
движения пуль и снарядов,
выпущенных из
огнестрельного оружия,
ракетных снарядов и
баллистических ракет.

19. Классическая задача баллистики

связана с движением тела брошенного под
некоторым углом к горизонту.
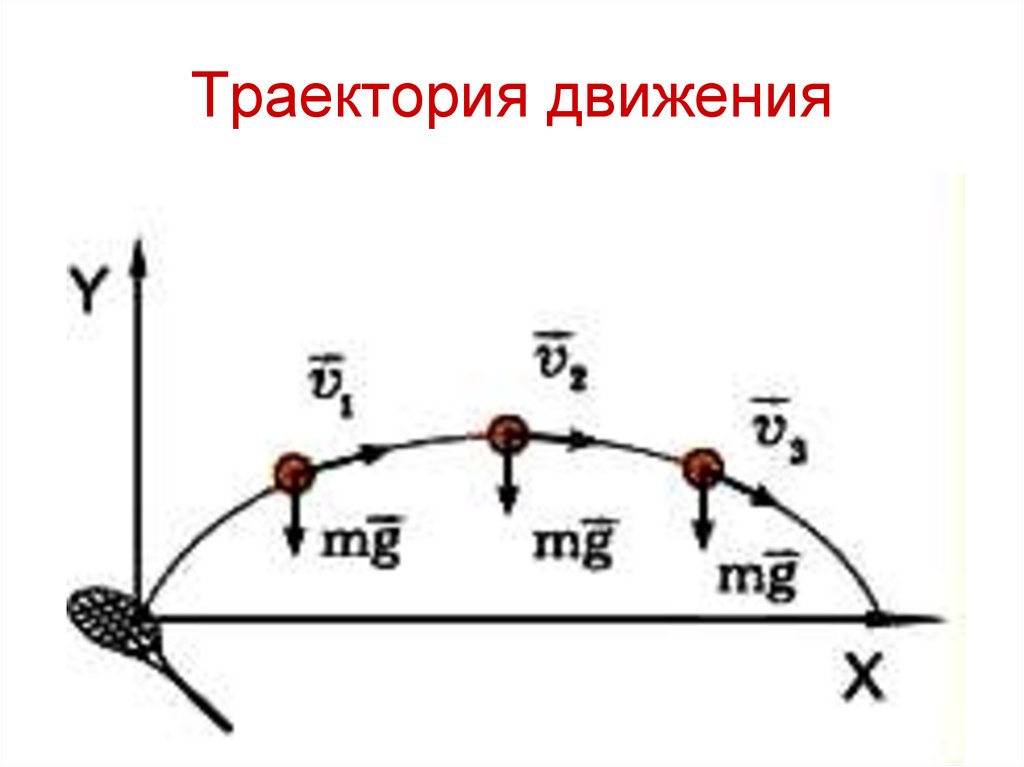
Тело совершает движение в двух плоскостях:
вдоль оси Х – равномерное,
вдоль оси У – равнопеременное.

20. Траектория движения

21. Кинематические уравнения движения.

Для оси Х :
х 0 х t
x 0 x const
x 0t cos
x 0 cos

22. Кинематические уравнения движения.

Для оси Y :
2
gt
y 0 y t
2
y 0 gt
y
2
gt
y 0t sin
2
y 0 sin gt

23. Уравнение траектории.

x 0t cos
2
gt
y 0t sin
2
x
t
0 cos
x sin g
x
y 0
0 cos 2 0 cos
2

24.

2
gx
y xtg 2
2
2 0 cos
Это уравнение параболы, опрокинутой «чашей» на ось
абсцисс(Х). Точки пересечения с осью определяют
начальный и конечный момент времени движения тела.

25. Основные характеристики КЗБ.

Движение тела при КЗБ характеризуют
временем полета (t), дальностью полета (S)
и высотой (h).
y 0 x 0(начало), x S (конец )
gx
x(tg 2
) 0
2
2 0 cos
sin
gx
2
cos 2 0 cos 2
2 sin cos
sin 2
x
S
g
g
2
0
2
0

26. Зависимость дальности от скорости.

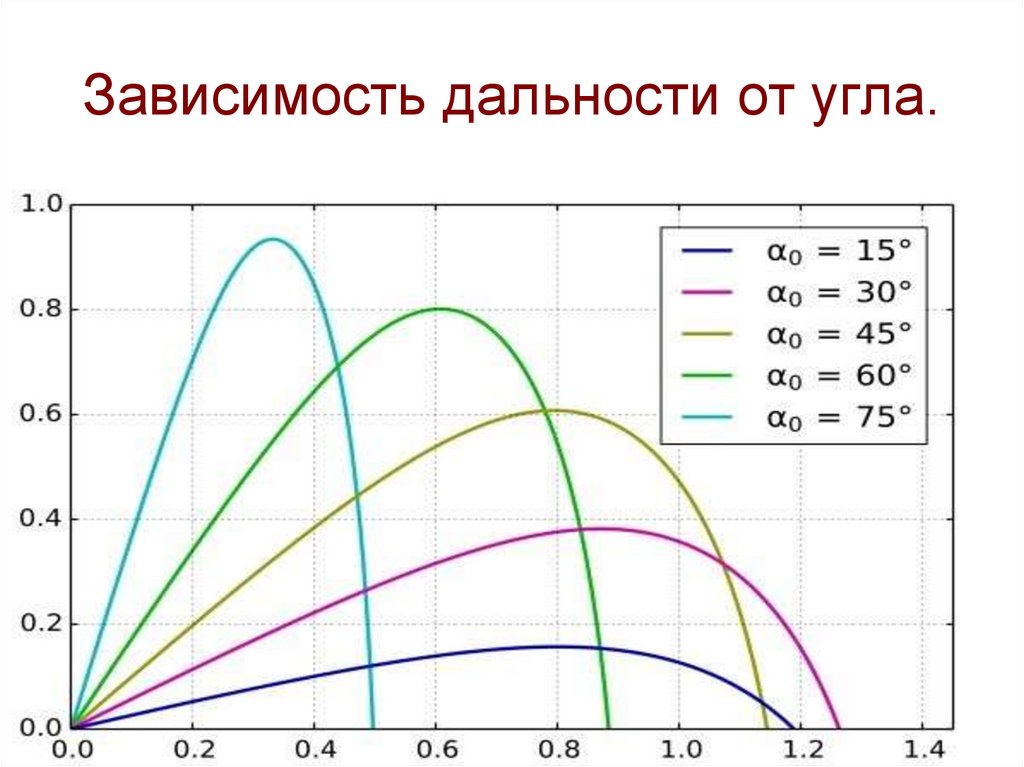
27. Зависимость дальности от угла.

28.

2 02 sin cos 2 0 sin
x
t
0 cos
g 0 cos
g
S
y( ) h
2
2
2 sin cos
2 sin cos sin
g
h
2
2
2g
cos 2 0 cos
2g
2
0
2
0
02 sin 2
2g

29.

• Свободное падение можно рассматривать,
как
частный случай КЗБ при заданном угле
бросания =
рад
2
2 0 sin
2 0
t
t
g
g
2
sin 1
0 sin 2
S 0
S
g
2
sin 2 0
2
0
2
2
h
0 sin
2g
h
2g

30.

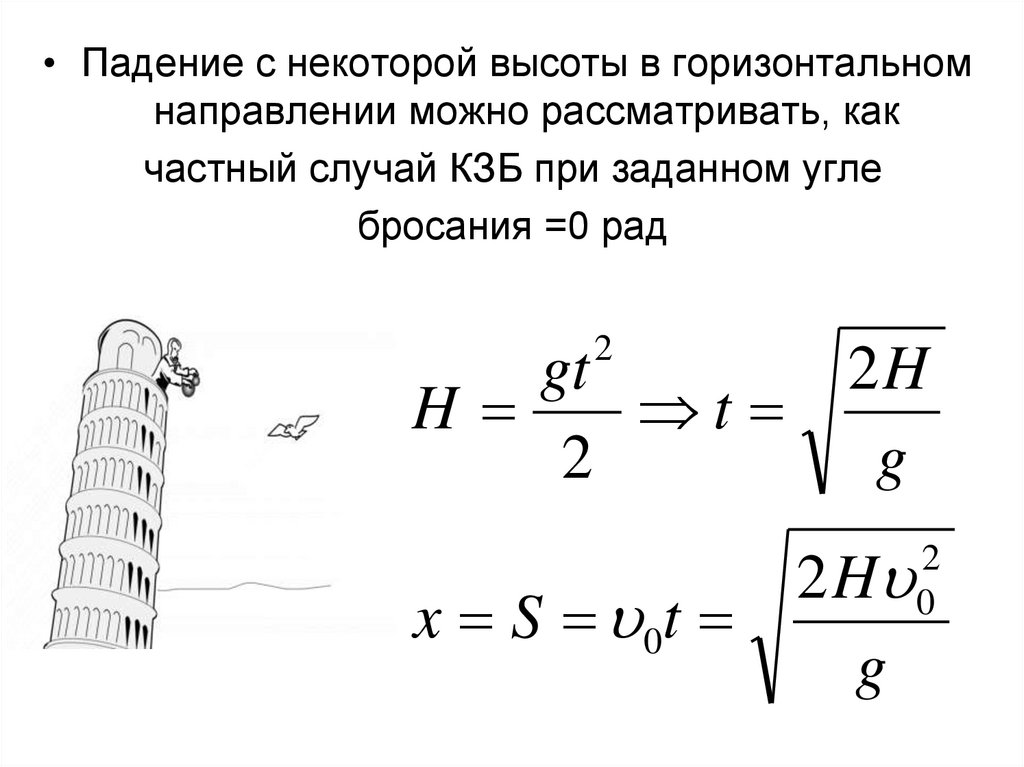
• Падение с некоторой высоты в горизонтальном
направлении можно рассматривать, как
частный случай КЗБ при заданном угле
бросания =0 рад
2
gt
H
t
2
2H
g
x S 0t
2 H
g
2
0