Координаты вектора

1.

Координаты вектора

2.

• Если векторы a и b коллинеарны и a ≠ 0, то
существует такое число k, что b = ka
• Пусть a и b – два данных вектора. Если
вектор p представлен в виде p = xa + yb,
где x и y – числа, то говорят вектор p
разложен по векторам a и b.
• Числа x и y называются коэффициентами
разложения.
• Любой вектор можно разложить по двум
неколиннеарным векторам, причем
коэффициенты разложения единственны

3.

• Векторы i и j называются
• В прямоугольной
координатными
системе координат
отложим от точки О векторами.
единичные векторы • i ↑↑Ox, │i│=1; j↑↑Oy, │j│=1
iиj
• p = xi + yj
• p {x; y} – где x, y
координаты вектора p
• Например:
• ОА = 4i + 5j => ОА {4; 5}
• ОВ = -6i + 2j => OB {-6; 2}
c {5; -3}
• c = 5i – 3j =>
ОА – радиус-вектор
• 0 = o∙ i + o∙ j => 0 {0; 0}

4.

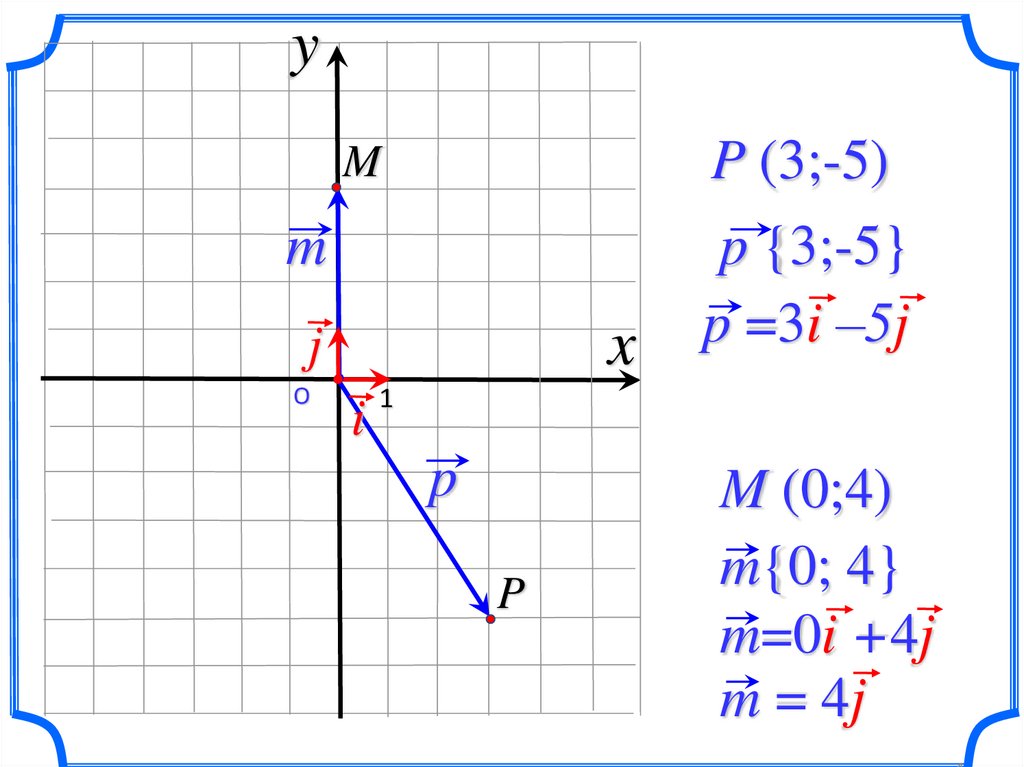
y
P (3;-5)
M
m
x
j
О
i
p {3;-5}
p =3i –5j
1
p
P
M (0;4)
m{0; 4}
m=0i +4j
m = 4j

5.

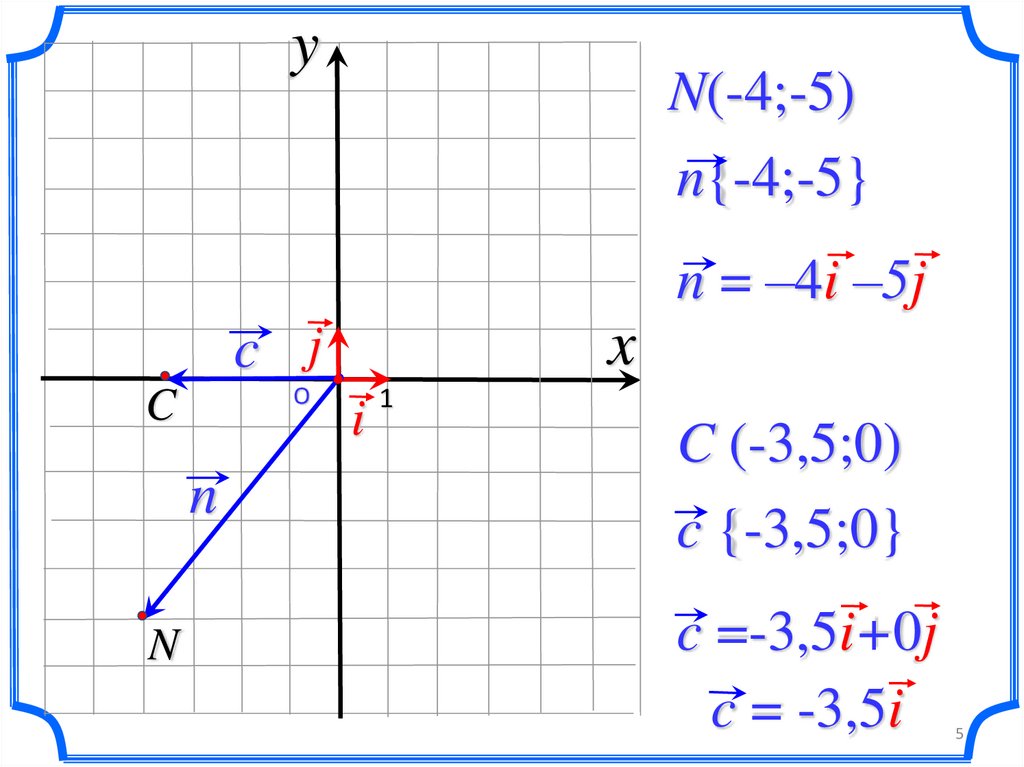
y
N(-4;-5)
n{-4;-5}
n = –4i –5j
x
c j
О
C
n
N
i
1
C (-3,5;0)
c {-3,5;0}
c =-3,5i+0j
c = -3,5i
5

6.

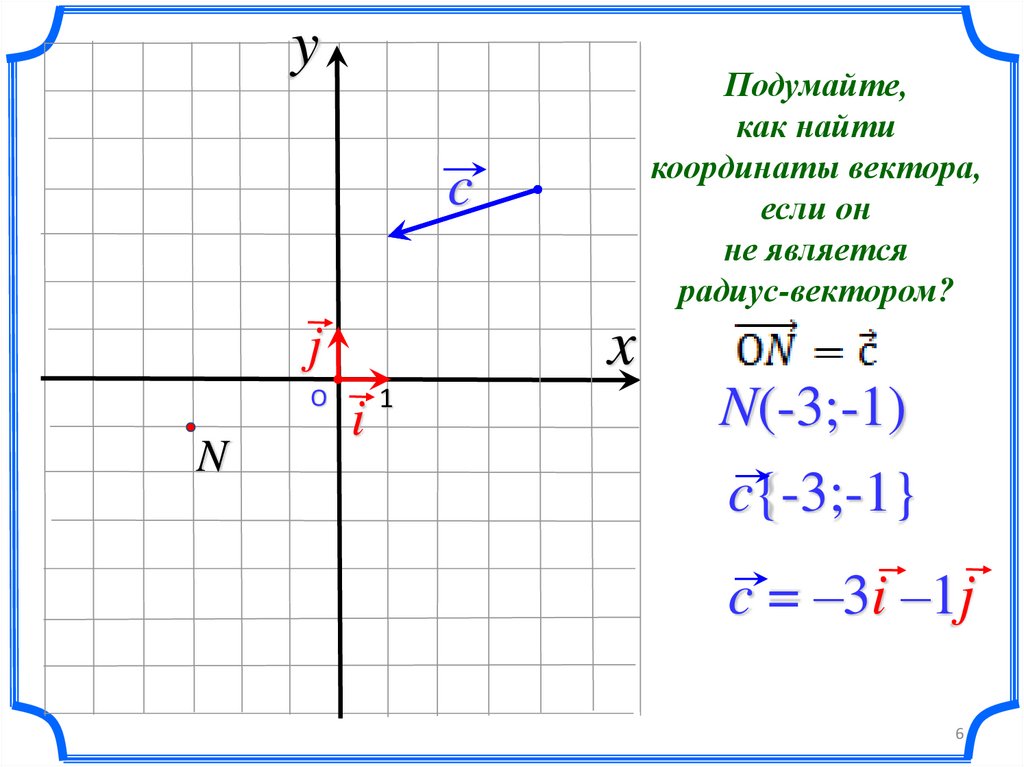
y
Подумайте,
как найти
координаты вектора,
если он
не является
радиус-вектором?
c
x
j
О
N
i
1
N(-3;-1)
c{-3;-1}
c = –3i –1j
6

7.

Свойства:
• Если векторы a = xi + yj и b = ki + lj равны,
то x = k и y = l. Координаты равных
векторов соответственно равны.
• Каждая координата суммы двух или
векторов равна сумме соответствующих
координат этих векторов.
• Каждая координата разности двух или
векторов равна разности
соответствующих координат этих
векторов.

8.

• Каждая координата произведения
вектора на число равна произведению
соответствующей координаты вектора
на это число.
• Пример:
Найти координаты вектора
если известно, что

9.

Координаты вектора
a {-6; 9}
n {-8; 0}
c {0; -7}
m{4; -3}
? r {-5;-8}
? s {-7; 0}
? e {0; 21}
? q {0; 0}
Разложение вектора по
координатным векторам
? a = – 6i+9j
? n = – 8i+0j
? c = 0i –7j
? m =4i –3j
r = –5i –8j
s = –7i+0j
e = 0i +21j
q =0i +0j
9

10.

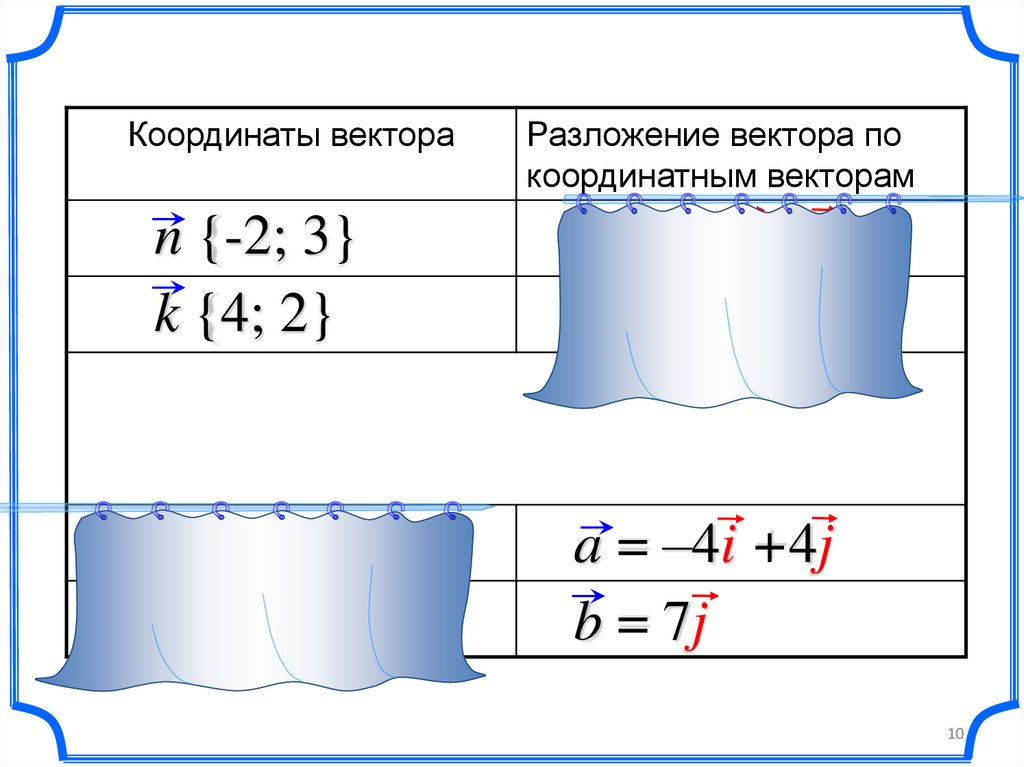
Координаты вектора
Разложение вектора по
координатным векторам
n {-2; 3}
k {4; 2}
n = – 2i+3j
k = 4i+2j
a {-4; 4}
b {0; 7}
a = –4i +4j
b = 7j
10

11.

y
c
b
f
a
j
О
x
i
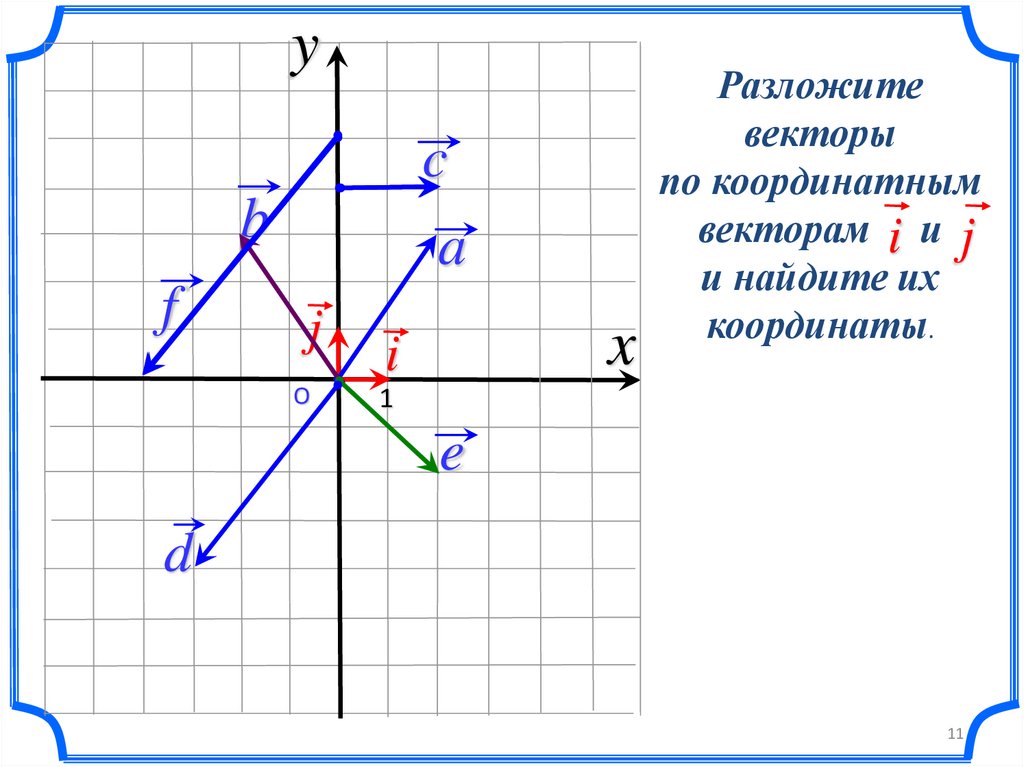
Разложите
векторы
по координатным
векторам i и j
и найдите их
координаты.
1
e
d
11

12.

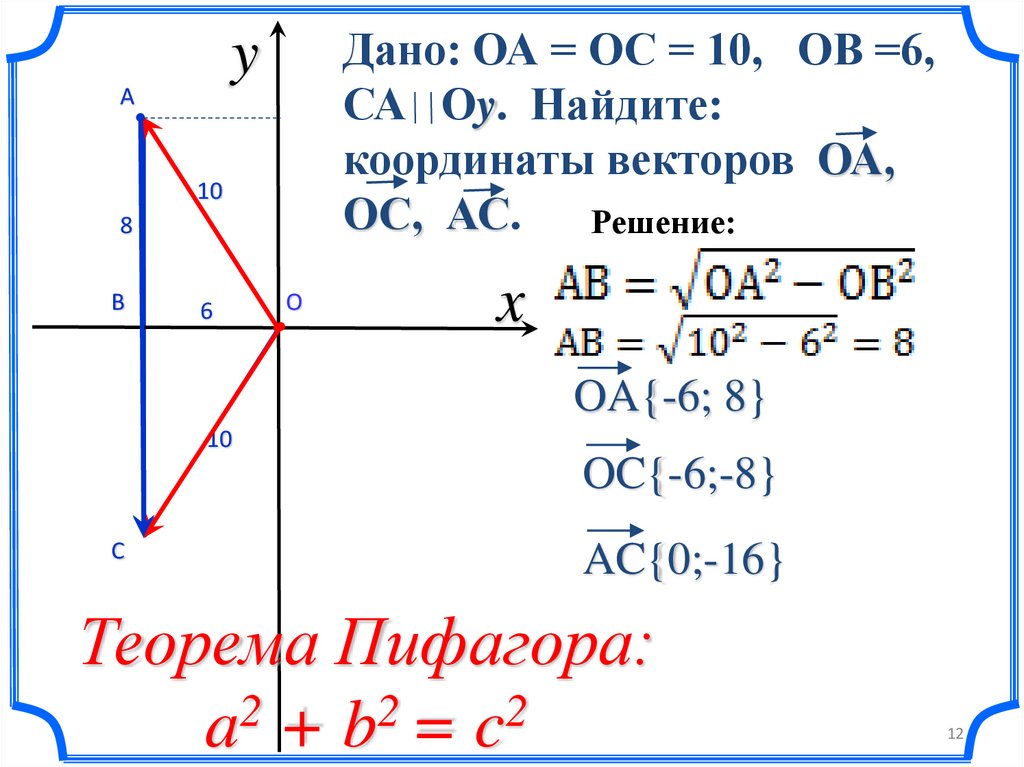
Дано: ОА = ОС = 10, ОВ =6,
СА Оy. Найдите:
координаты векторов ОА,
ОС, АС.
Решение:
y
А
10
8
В
6
О
x
OA{-6; 8}
10
OC{-6;-8}
С
AC{0;-16}
Теорема Пифагора:
2
2
2
a +b =c
12