Координаты вектора. Параллелограмм

1.

1

2.

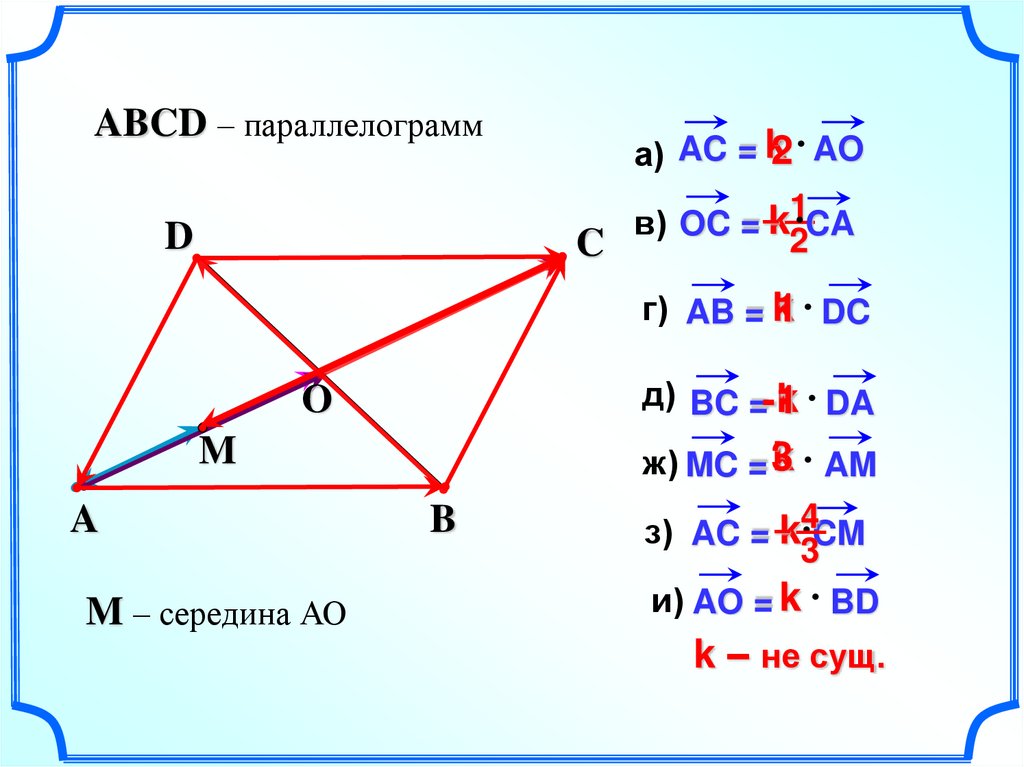
ABCD – параллелограмм
а) AC = k2 AO
в) OC = –k1 CA
2
C
D
г) AB = k
1 DC
д) BC =-1
k DA
O
k AM
ж) MC = 3
M
A
M – середина АО
B
з) AC = –k 4CM
3
и) AO = k BD
k – не сущ.

3.

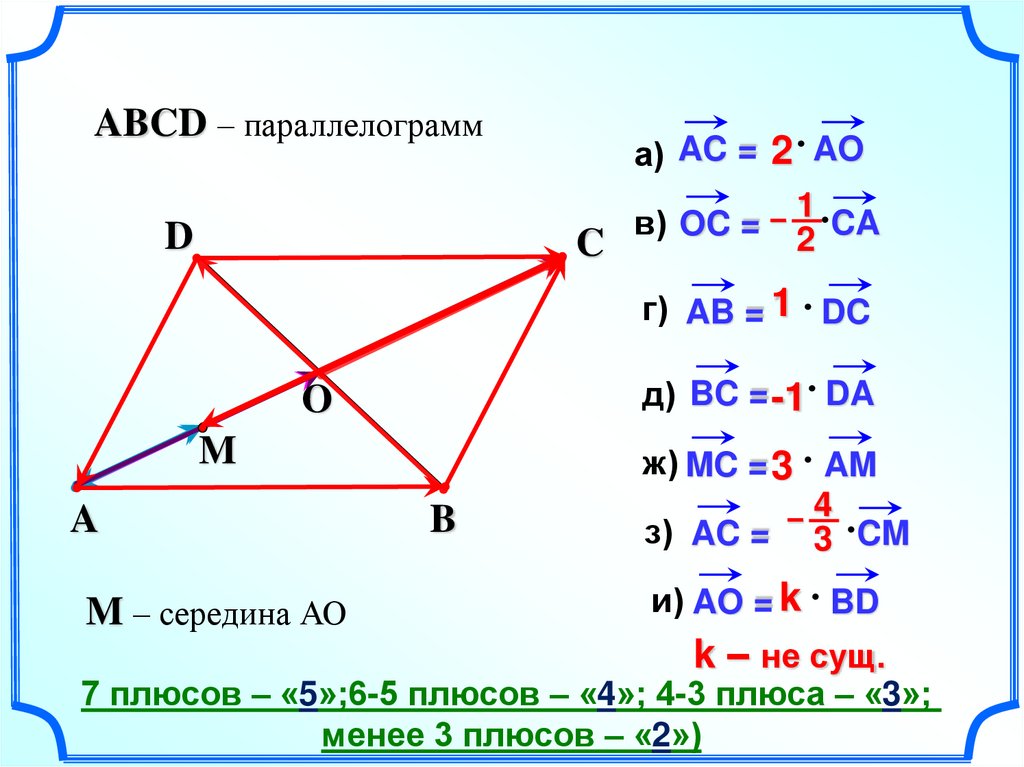
ABCD – параллелограмм
D
а) AC = 2 AO
1
в) OC = – 2 CA
C
г) AB = 1 DC
д) BC = -1 DA
O
M
A
M – середина АО
B
ж) MC = 3 AM
–4
з) AC = 3 CM
и) AO = k BD
k – не сущ.
7 плюсов – «5»;6-5 плюсов – «4»; 4-3 плюса – «3»;
менее 3 плюсов – «2»)

4.

4

5.

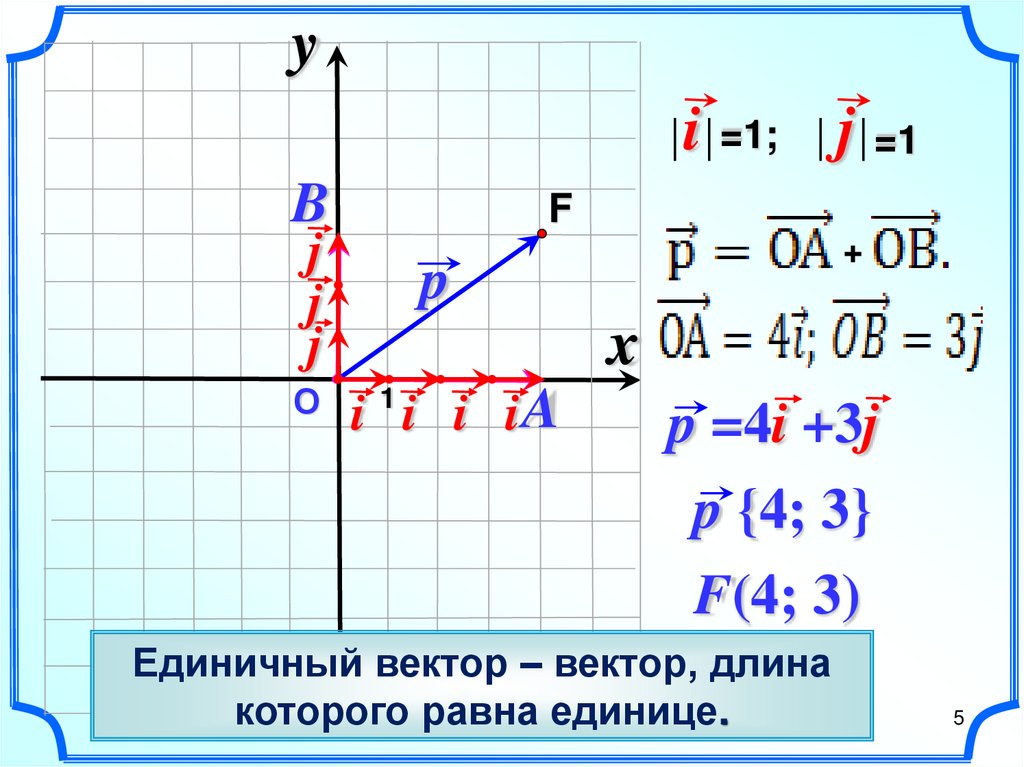
y
i =1; j =1
B
F
j
j
j
О
+
p
x
1
i i i iA
p =4i +3j
p {4; 3}
F(4; 3)
Единичный вектор – вектор, длина
которого равна единице.
5

6.

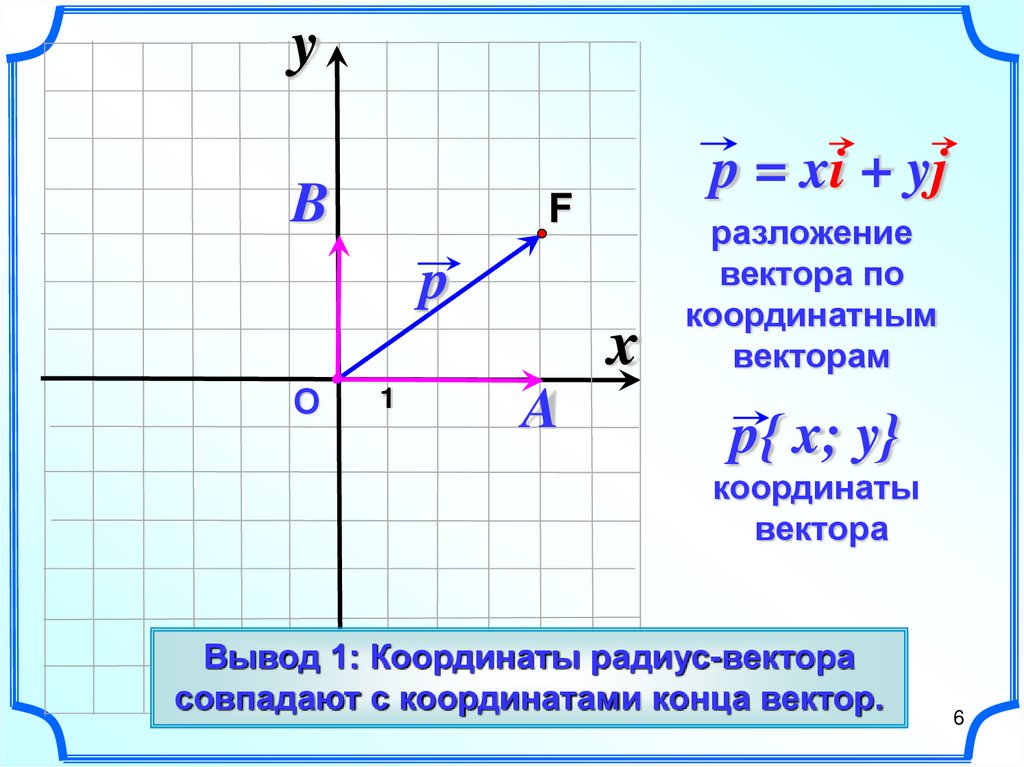
y
B
p = xi + yj
F
p
x
О
1
A
разложение
вектора по
координатным
векторам
p{ x; y}
координаты
вектора
Вывод 1: Координаты
Радиус-вектор
– вектор радиус-вектора
начало которого
совпадают
с координатами
конца вектор.
совпадает
с началом координат.
6

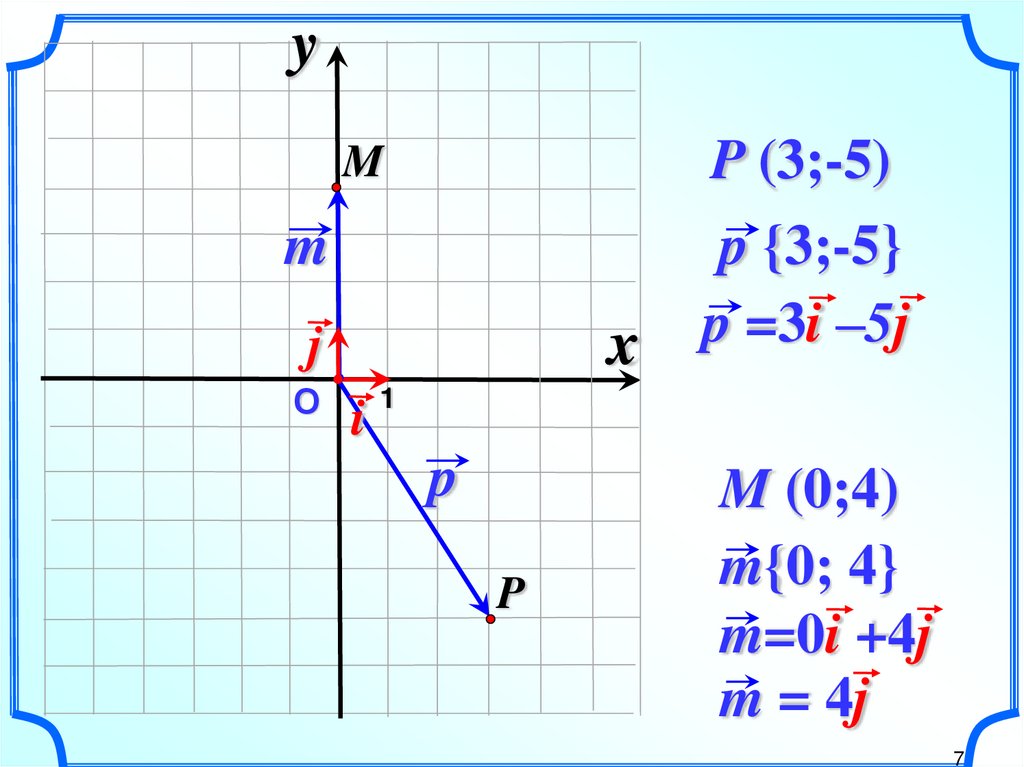
7.

y
P (3;-5)
M
m
x
j
О
i
p {3;-5}
p =3i –5j
1
p
P
M (0;4)
m{0; 4}
m=0i +4j
m = 4j
7

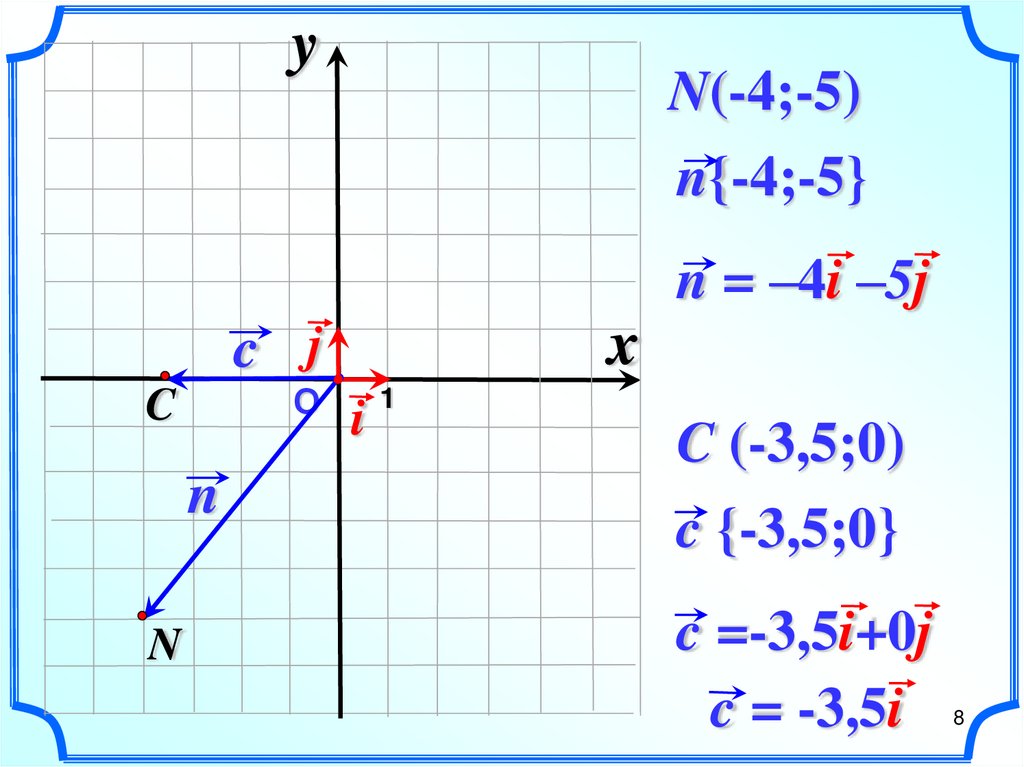
8.

y
N(-4;-5)
n{-4;-5}
n = –4i –5j
x
c j
О
C
n
N
i
1
C (-3,5;0)
c {-3,5;0}
c =-3,5i+0j
c = -3,5i
8

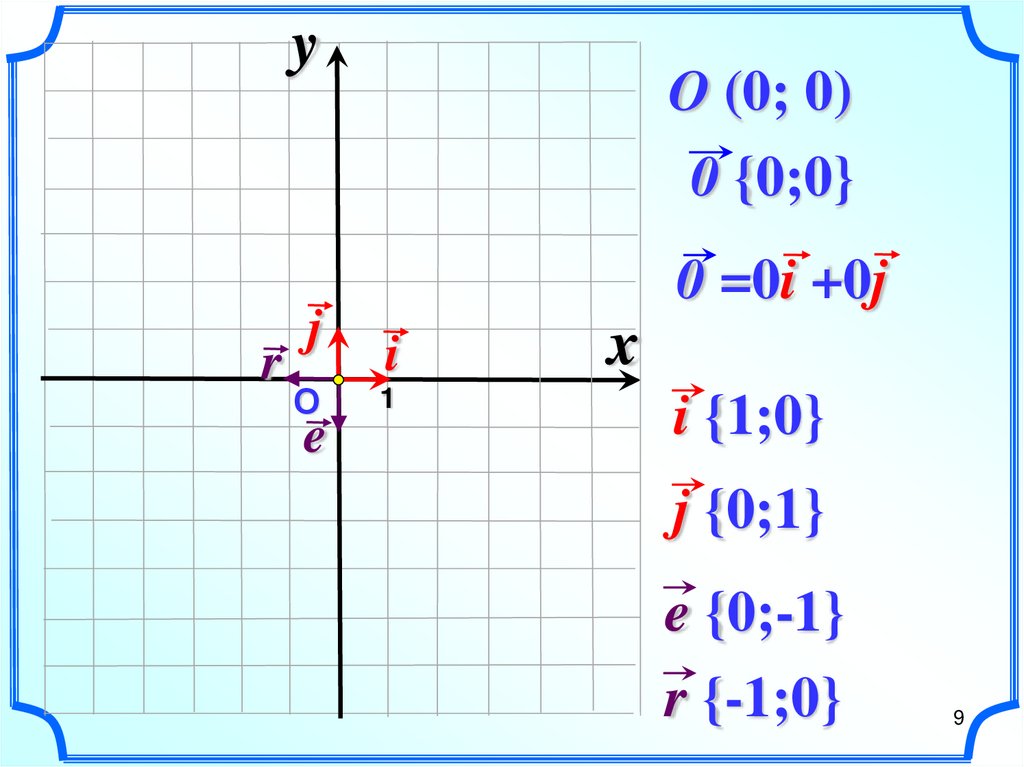
9.

y
O (0; 0)
0 {0;0}
r
j
О
e
0 =0i +0j
i
1
x
i {1;0}
j {0;1}
e {0;-1}
r {-1;0}
9

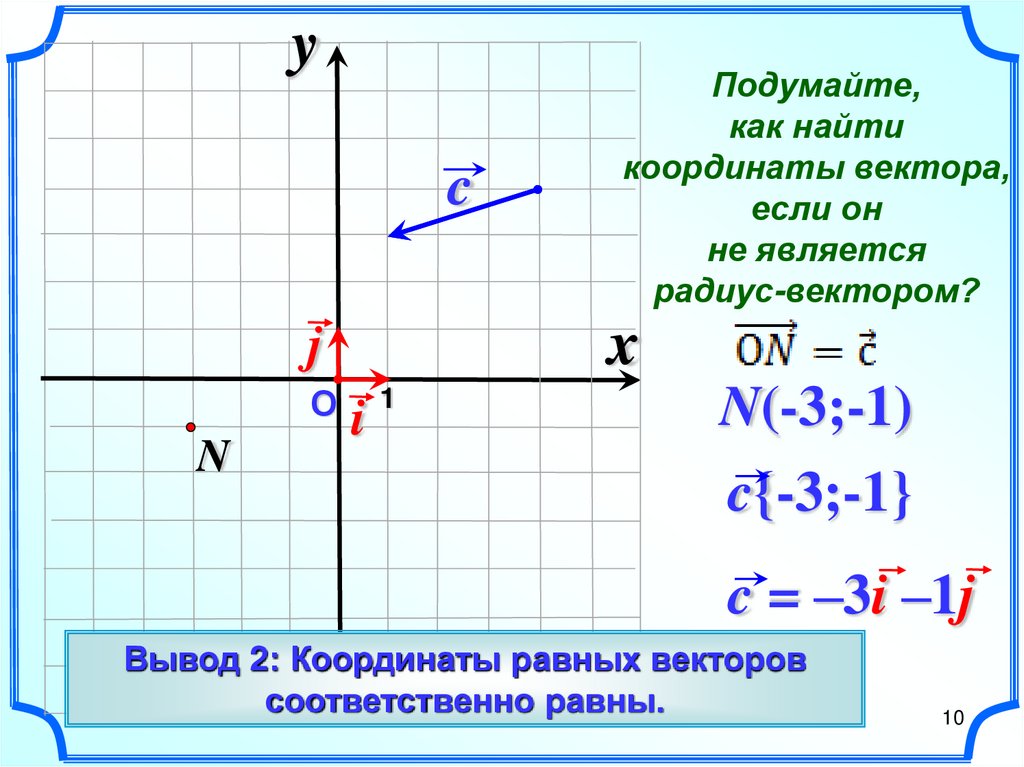
10.

y
c
x
j
О
N
Подумайте,
как найти
координаты вектора,
если он
не является
радиус-вектором?
i
1
N(-3;-1)
c{-3;-1}
c = –3i –1j
Вывод 2: Координаты равных векторов
соответственно равны.
10

11.

11

12.

Координаты вектора
?
?
?
?
a {-6; 9}
n {-8; 0}
c {0; -7}
m{4; -3}
r {-5;-8}
s {-7; 0}
e {0; 21}
q {0; 0}
Разложение вектора по
координатным векторам
? a = – 6i+9j
? n = – 8i+0j
? c = 0i –7j
? m =4i –3j
r = –5i –8j
s = –7i+0j
e = 0i +21j
q =0i +0j
12

13.

13

14.

14

15.

Координаты вектора
Разложение вектора по
координатным векторам
n {-2; 3}
k {4; 2}
n = – 2i+3j
k = 4i+2j
a {-4; 4}
b {0; 7}
a = –4i +4j
b = 7j
15

16.

y
1) Какой из данных
векторов равен вектору
4i –2j
ОС =
2) Напишите разложение
A
F
B
j
О
x iиj
i
1
C
E
D
-4i -2j
вектора ОЕ =
по координатным векторам
H
3) Найдите координаты
вектора ОА
{2;4}
4) Какой вектор имеет
координаты ОF =
{-4;2}
5) Отложите от т.О вектор
ОH с координатами
16
{2;-4}

17.

17

18.

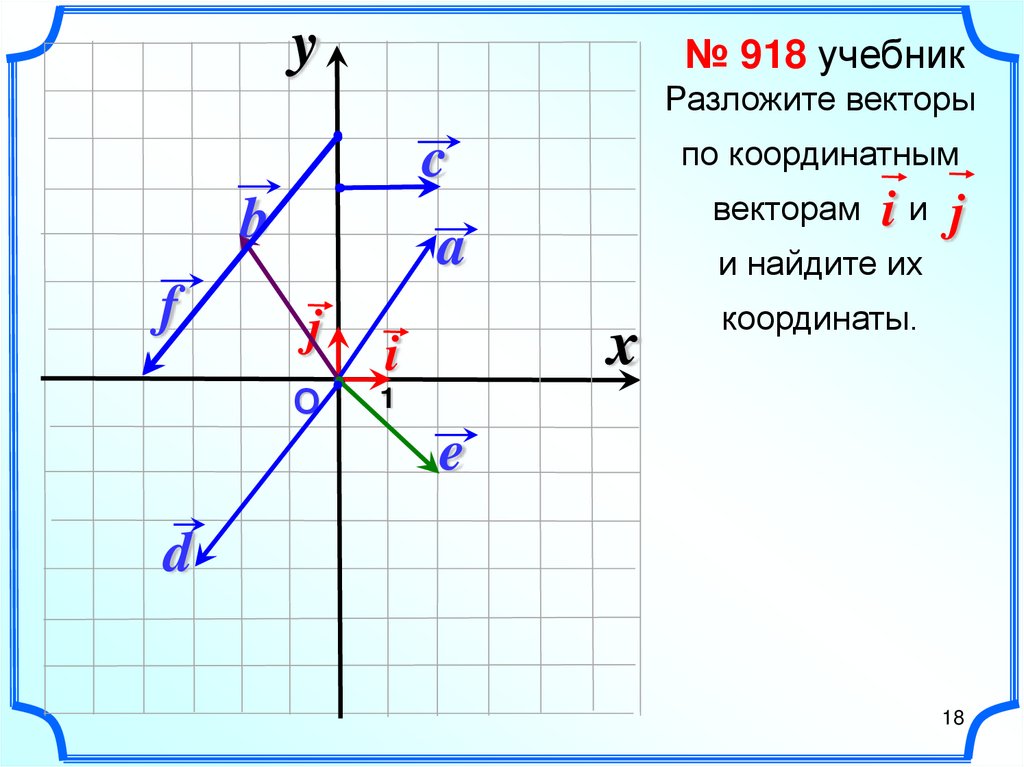
y
№ 918 учебник
Разложите векторы
по координатным
c
b
f
векторам
a
j
О
и найдите их
x
i
iи j
координаты.
1
e
d
18

19.

y
А
Дано: ОА = ОС = 10, ОВ =6, СА Оy.
Найдите:
координаты векторов ОА, ОС, АС.
10
Решение:
8
В
6
О
x
OA{-6; 8}
10
С
OC{-6;-8}
AC{0;-16}
Теорема Пифагора:
2
2
2
a +b =c
19

20.

Рефлексия
Выбери вариант соответствующий
твоим ощущениям после сегодняшнего
занятия.
1. Я все знаю, понял и могу объяснить
другим!
2. Я все знаю, понял, но не уверен, что
смогу объяснить другому.
3. Я сам знаю, понял, но объяснить
другому не смогу.
4. У меня остались некоторые вопросы.
Отрази свое настроение после
занятия , написав три слова.
20

21.

21