Численное решение линейных алгебраических уравнений. Часть 1

1.

ЧИСЛЕННОЕ РЕШЕНИЕ
ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
Прямые методы

2.

План
Постановка задачи
Классификация методов
решения СЛАУ
Прямые методы:
–
Метод Крамера
–
Метод Гаусса
–
Метод Жордана –
Гаусса
Габриэль Крамер
(Cramer)
Модификации методов
исключения неизвестных
Камиль Мари Эдмон
Жордан (Jordan)

3.

Постановка задачи
К решению задач линейной алгебры
приводит анализ физических систем
различной природы: механических,
гидравлических, электростатических и
т.п.
Системы линейных алгебраических
уравнений (СЛАУ) возникают при
обработке данных; дискретизации
линейных дифференциальных задач;
решении краевых задач; расчете
электрических цепей; в экономических
моделях и т.д.

4.

Постановка задачи
Дана система n линейных
алгебраических уравнений с
n неизвестными:
a11 x1 a12 x2 ... a1n xn f1
a x a x ... a x f
21 1 22 2
2n n
2
....
an1 x1 an 2 x2 ... ann xn f n
(1)

5.

Постановка задачи
или в матричном обозначении:
где
x1
x
2
X
...
xn
AX f
- искомый
вектор
(1’)
f1
f
2 - вектор
f
... правой части
f n

6.

Постановка задачи
Как известно из курса линейной алгебры,
если матрица A невырожденная, т.е.
det A 0
то система (1) имеет единственное решение:
1
X A f

7.

Методы решения СЛАУ
1.
2.
3.
Прямые (точные) методы: решение
находится за конечное число
арифметических действий. Точными их
можно назвать лишь абстрагируясь от
погрешностей округления.
Итерационные методы состоят в том, что
решение системы (1) определяется как
предел некоторой последовательности
приближений X k при k , где k – номер
итерации.
Вероятностные методы или методы
Монте-Карло используют для решения
систем с очень большим числом
неизвестных (>107).

8.

Методы
решения СЛАУ
ПРЯМЫЕ
УНИВЕРСАЛЬНЫЕ
ИТЕРАЦИОННЫЕ
СПЕЦИАЛЬНЫЕ
КРАМЕРА
КВАДРАТНОГО
КОРНЯ*
ГАУССА
ПРОГОНКИ**
ЖОРДАНА-ГАУССА
…
…
*матрица симметричная и положительно определенная
**матрица трехдиагональная
ВЕРОЯТНОСТНЫЕ

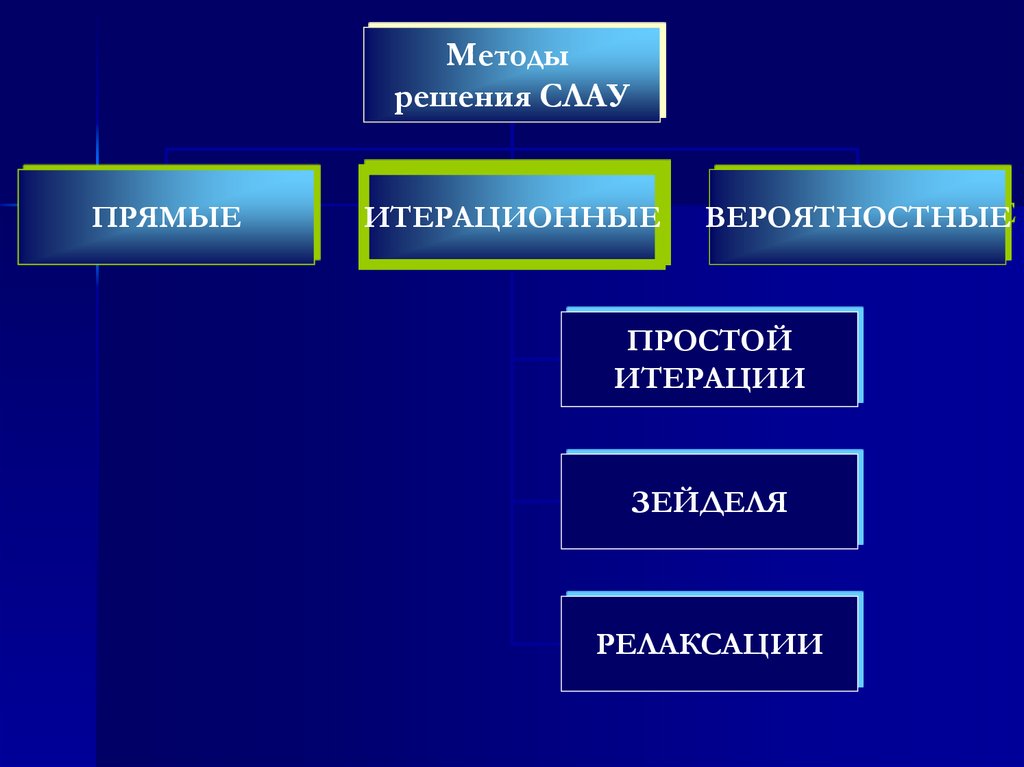
9.

Методы
решения СЛАУ
ПРЯМЫЕ
ИТЕРАЦИОННЫЕ
ВЕРОЯТНОСТНЫЕ
ПРОСТОЙ
ИТЕРАЦИИ
ЗЕЙДЕЛЯ
РЕЛАКСАЦИИ

10.

Метод Крамера
Универсальным прямым методом решения
систем вида (1), известным из курса алгебры,
является метод Крамера:
det Ai
xi
det A
Для реализации на ЭВМ этого метода
необходимо выполнить n n! - умножений для
каждого определителя. Подобным способом
можно пользоваться, если n невелико
(обычно< 5), в противном же случае такой
метод становится очень затратным.

11.

2 x1 3x2 x3 3,
Пример. Метод Крамера 3x1 2 x2 4 x3 13,
4 x x 2 x 7.
3
1 2
2
A := 3
4
-1
4
2
3
-2
1
A 3
2
A3 := 3
4
3
-2
1
A3 6
-3
A1 := 13
7
3
-2
1
A1 3
-3
13
7
-1
4
2
2
A2 := 3
A 3
4
-3
13
7
-1
4
2
A2 3
3
3
6
x1 1, x2
1, x3 2.
3
3
3

12.

Метод Гаусса
Запишем систему (1) в виде:
a11 a12
a21 a22
....
an1 an 2
a1n x1 f1
a2 n x2 f 2
... ...
ann xn f n
(2)
Предположим, что a11 0 , если иначе,
то переставим строки.

13.

Прямой ход метода
Гаусса
Исключим x1 из n-1 последних
уравнений, для этого из второго
уравнения вычтем первое,
умноженное на a 21
a11
Из третьего вычтем первое
умноженное на a
31
и т.д.
a11

14.

Прямой ход метода
Гаусса
Этот процесс приведет к системе:
a1n x1 f1
a11 a12
1
1
1
a 2 n x2 f 2
0 a 22
....
... ...
1
1
0 a1
a nn xn f n
n2
(3)
При исключении x1 преобразованию
подвергаются строки расширенной
матрицы, включая свободные члены.

15.

Прямой ход метода
Гаусса
Если a122 0,
0
то применим a11
аналогичный 0
процесс к
0
последующим
уравнениям и .
исключим x2
0
из n-2
уравнений.
0
a12
1
22
a
0
.
0
... a1n x1 f1
1
1
... a2 n x2 f 2
f2
2
x
... a3n
3 3
.
. ... ...
2
2
... ann xn f n
0

16.

Прямой ход метода Гаусса
a110 a120
1
0 a22
.
.
0
0
0
0
.
.
0
0
... a10k
a10k 1
1
1
... a2 k
a2 k 1
.
.
.
... akkk 1 akkk 11
... 0 akk 1k 1
.
.
.
0
0
ankk 1
... a10n x1 f1
f1
1
... a2 n x2 2
.
. ... ...
k 1
k 1
... akn xk f k
k
k
xk 1
... ak 1n
f k 1
.
. ... ...
k
... ann xn f k
n
k – тый шаг

17.

Прямой ход метода
Гаусса
Выпишем в общем виде рекуррентные
соотношения для получения
коэффициентов матрицы на k -м шаге:
aik j aik j 1
f i k f i k 1
akk j1 aik k 1
akk k1
f kk 1 aik k 1
akk k1
k 1, 2,..., n 1;
i, j k 1, k 2,..., n;

18.

Смысл индексов
k 1
i j
a a
k
i j
fi fi
k
k 1
k 1
k j
a
k 1
ik
a
akk k1
f kk 1 aik k 1
akk k1
k – номер того уравнения,
которое вычитается из
остальных и номер того
неизвестного, которое
исключается из последующих
уравнений;
akkk 1 - называется
разрешающим элементом;
i – номер уравнения из
которого в данный момент
исключается неизвестное;
j – текущий номер столбца.

19.

Прямой ход метода Гаусса
Через n-1 шаг система будет
приведена к треугольному виду, при
этом прямой ход метода Гаусса
завершен.
a11
A0
f
0
0
b A1
a11
f1
00
a11
a122
A2
f2
……
00
a122
An-1 fn-1
Схематическая иллюстрация прямого хода метода Гаусса

20.

Обратный ход метода
Гаусса
Осуществляется для нахождения
неизвестных системы.
Из последнего уравнения находится
xn. Его значение подставляется в n-1
уравнение …
и т. д. до первого уравнения и х1.

21.

Обратный ход
Искомое решение системы (1)
определяется по формулам:
n
f n( n 1)
xn ( n 1) , xk
ann
f k( k 1) akj( k 1) x j
j k 1
( k 1)
kk
a
; k n 1, n 2,...,1
Весь алгоритм метода Гаусса
осуществляется за порядка
арифметических операций.
n3
3

22.

Пример. Метод Гаусса
Методом Гаусса решить систему
уравнений:
2 x1 3x2 x3 3,
3x1 2 x2 4 x3 13,
4 x x 2 x 7.
3
1 2

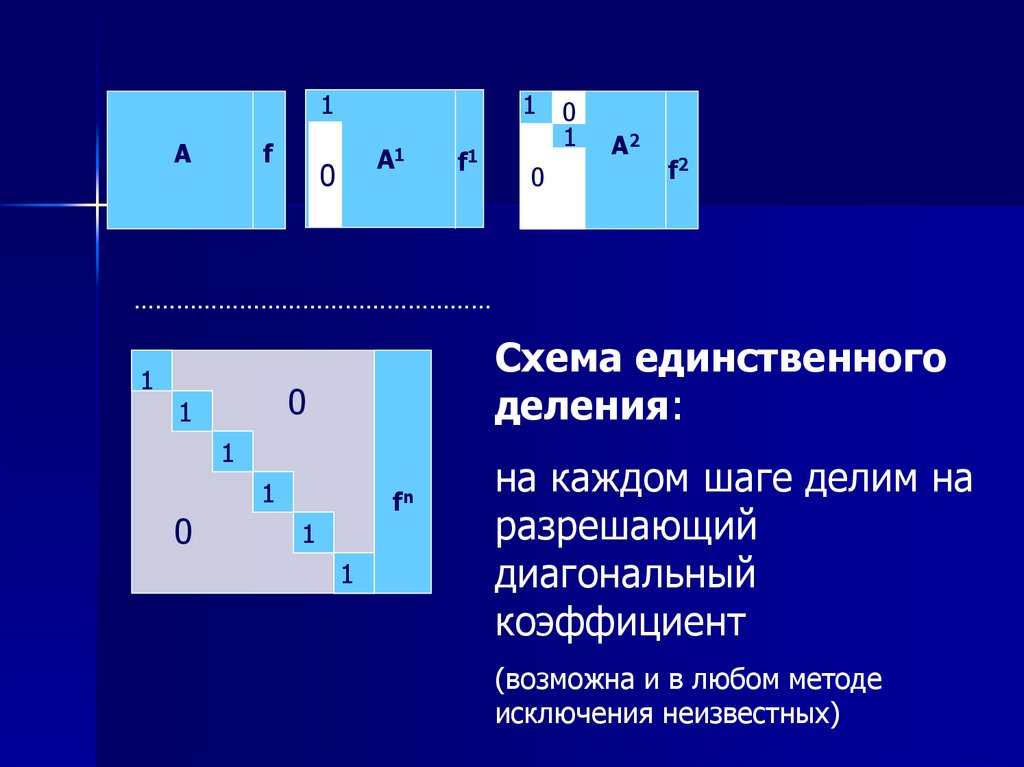
23.

Пример. Метод Гаусса (со схемой
единственного деления*)
2 3 1 3
3 2 4 13
4 1 2 7
3
1
1 2
2
0 1 11
13
0 5 4
3
2
35
13
13
3
1
2
3 2
4 1
1 3
2
2
4 13
2
7
3
1 2
0 1
0 0
1
2
11
13
3
13
3
2
35
13
6
13
1
0
0
3
2
13
2
5
3
1
2
0 1
0 0
1 3
2
2
11 35
2
2
4 13
1
2
11
13
1
3
2
35
13
2
* Схема единственного деления применяется для получения 1 на диагонали путем деления на
разрешающий элемент

24.

Метод Жордана – Гаусса
Идея модификации метода Гаусса состоит
в том, чтобы одновременно осуществить
прямой и обратный ход, приведя
исходную матрицу к диагональному виду.
Если при этом на главной диагонали
будут 1, то искомое решение – вектор
свободных членов. Схематически метод
выглядит следующим образом:

25.

a111
A
f
0
A1
f1
a111 0 0
a222
2
0
A2 f
0
……………………………………………
a111
a222
0
.
.
0
fn
.
annn
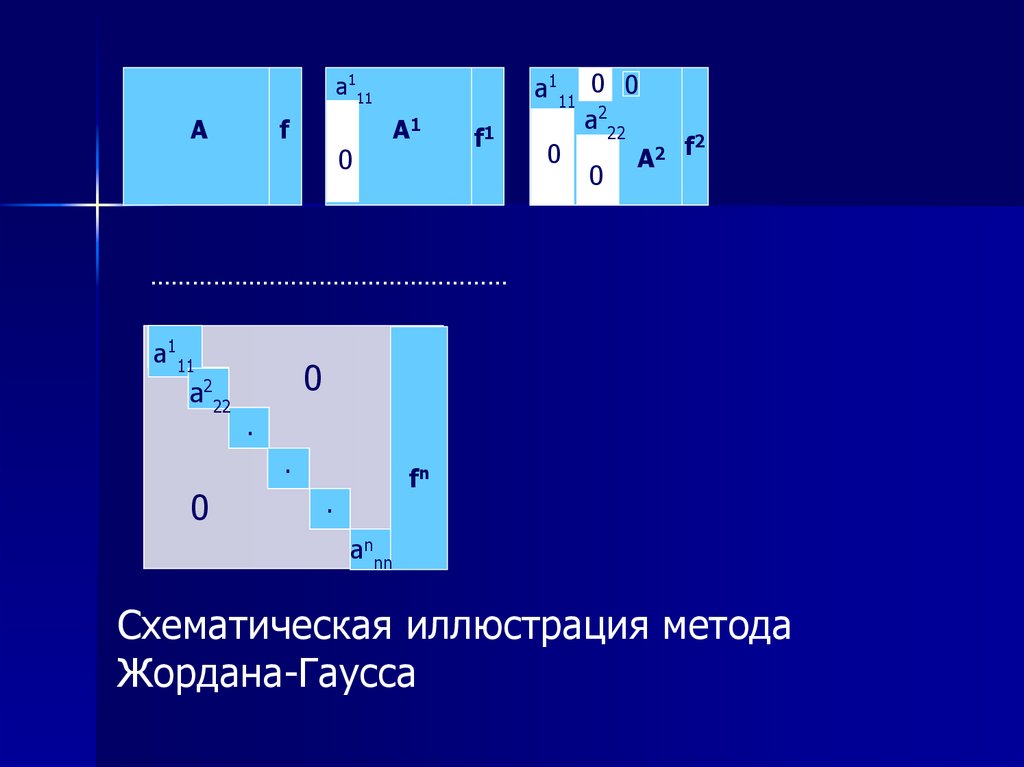
Схематическая иллюстрация метода
Жордана-Гаусса

26.

Метод Жордана – Гаусса
k
ij
k 1
ij
a
k 1
kj
k 1
kj
a a
k
ij
a
a
k 1
kj
k 1
kj
a
a
aikk 1 , i, j k
k 1
ik
k 1
kj
a
, i k, j k; a
a
k
ij
,i k, j k
a aij , i, j 1, 2,..., n.
0
ij