Похожие презентации:
Системы линейных алгебраических уравнений
1.
§4. Системы линейныхалгебраических уравнений
п.1. Основные определения.
Системой из m линейных алгебраических
уравнений с n неизвестными называется
система вида
a11 x1 a12 x2 a1n xn b1 ,
a21 x1 a22 x2 a2 n xn b2 ,
am1 x1 am 2 x2 amn xn bm .
aij , i 1, m , j 1, n; x j , j 1, n; bi , i 1, m.
2.
a11 a12a21 a22
A
a
m1 am 2
a1n
a2 n
amn
─ матрица
коэффициентов
x1
x2
X
x
n
─ столбец
неизвестных
a11
a21
A
...
a
m1
a12
... a1n
a22
... a2 n
...
...
...
am 2 ... amn
b1
b2
...
bm
─ расширенная
матрица
b1 коэффициентов
b2
B
b
m
─ столбец свободных
членов
3.
a11 a12a21 a22
a
m1 am 2
a1n x1 b1
a2 n x2 b2 ─ матричная
форма записи
amn xn bm системы
A X B
─ операторная форма записи
системы
4.
Решением системы называется совокупностьn чисел
x1 c1 , x 2 c 2 , ..., x n c n ,
при подстановке которых все уравнения
системы обращаются в верные равенства.
Система называется совместной, если она
имеет хотя бы одно решение.
Система называется несовместной, если
она не имеет решений.
Решить систему — значит найти все решения
системы или показать, что она несовместна.
5.
Теорема 1 (Кронекера-Капелли).Система линейных уравнений совместна тогда
и только тогда, когда ранг матрицы
коэффициентов равен рангу расширенной
матрицы коэффициентов,
r ( A ) r ( A ).
6.
Теорема 2.Если ранг матрицы коэффициентов
совместной системы равен количеству
неизвестных,
r ( A) n,
то система имеет единственное решение.
Теорема 3.
Если ранг матрицы коэффициентов
совместной системы меньше количества
неизвестных,
r ( A) n,
то система имеет бесконечное количество
решений.
7.
Пример. Найти количество решений системыx1 2 x2 x3 x4 2,
2 x1 x2 x3 x4 1,
x 7 x 4 x 4 x 3.
2
3
4
1
Решение.
1 2 1 1 2 1 2 1 1 2
2 1 1 1 1 ~ 0 5 3 3 3 ~
1 7 4 4 3 0 5 3 3 1
1 2 1 1 2 Значит, r ( A ) r ( A ),
~ 0 5 3 3 3 . т.е. система не имеет
0 0
решений.
0
0
2
8.
п.2. Решение СЛУ.Рассмотрим систему
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
an1 x1 an 2 x2 ann xn bn .
Пусть
det A 0 .
9.
A X BТак как det A 0 , то существует обратная
1
матрица A .
Тогда
1
1
A A X A B
1
E X A B
1
X A B
(1)
Решение системы по формуле (1) называют
матричным способом.
10.
Пример.2 x1 3 x2 x3 7,
x1 2 x2 x3 2,
x
2 x3 3.
1
Решение.
3 1
2
A 1 2
1
1
0
2
7
B 2
3
1
4 6
1
1
A
5 3
1
13
2
3
7
11.
1 74 6
1
1
5 3 2
X A B
1
13
3 7 3
2
13 1
1
26 2
13
13 1
12.
Правило КрамераИспользуя формулу для нахождения обратной
матрицы формулу (1) перепишем в виде:
x1
A11
x2 1 A12
...
x
A
n
1n
или
An1 b1
An 2 b2
,
...
Ann bn
A21
A22
A2 n
b1 A11 b2 A21 ... bn An1
x1
x2 b1 A12 b2 A22 ... bn An 2
.
...
...
x b A b A ... b A
n nn
n 1 1n 2 2 n
13.
Значит,b1 A11 b2 A21 ... bn An1
b1 A1n b2 A2 n ... bn Ann
x1
,..., x n
.
Рассмотрим определитель
b1 a12
b2 a22
1
bn an 2
a1n
a2 n
.
ann
Применив теорему Лапласа, разложим его по
элементам первого столбца:
Тогда
1 b1 A11 b2 A21 ... bn An1 .
1
x1 .
14.
Аналогично,n
2
x2
,..., x n
.
Формулы
xj
j
,
j 1, n,
называются формулами Крамера.
15.
2 x1 3 x2 x3 7,x1 2 x2 x3 2,
x
2 x3 3.
1
Пример.
2 3 3 1 1
2
2
3 1
2
7
1 13
0
7
7 1
2 1 2
1
3
1 2
1
2
1 2 2
3
0
1 13
2
3
1 26
3 1 2 2 13
1
0
3
16.
1 13x1
1
13
2 26
x2
2
13
3 13
x3
1
13
17.
Метод ГауссаРассмотрим систему
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1 22 2
2n n
2
am1 x1 am 2 x2 amn xn bm .
Процесс решения состоит из двух этапов:
1) прямой ход;
2) обратный ход.
(2)
18.
1) Прямой ход.Задача: привести систему к ступенчатому виду
a11 x1 a12 x2 a1n xn b1 ,
a22 x2 a2 n xn b2 ,
akk xk akn xn bk .
1-й шаг.
Пусть в системе (2) a11 0 (иначе переставим
уравнения) .
Исключим неизвестную x1 из всех уравнений
(кроме 1-го).
19.
a11 x1 a12 x2 a1n xn b1 ,a x a x a x b ,
21 1 22 2
2n n
2
am1 x1 am 2 x2 amn xn bm .
Умножим 1-е уравнение на
и сложим со 2-м.
Умножим 1-е уравнение на
и сложим с 3-м и т.д.
a21
a11
a31
a11
20.
Получим системуa11 x1 a12 x2 a1n xn b1 ,
(1)
(1)
(1)
a22 x2 a2 n xn b2 ,
(1)
(1)
(1)
am 2 x2 amn xn bm .
Аналогично исключим неизвестную x2 из всех
уравнений кроме 1-го и 2-го.
Продолжая таким образом, получим
ступенчатую систему.
21.
Замечание 1.Если в прямом методе получается уравнение
вида
0 0,
то его отбрасываем.
Замечание 2.
Если в прямом методе получается уравнение
вида
0 d , d 0,
то система несовместна.
22.
Замечание 3.Если в ступенчатой системе
k n,
то система имеет единственное решение (см.
теорему 2).
Замечание 4.
Если в ступенчатой системе
k n,
то система имеет бесконечное множество
решений (см. теорему 3).
23.
2) Обратный ход.a11 x1 a12 x2 a1n xn b1 ,
a22 x2 a2 n xn b2 ,
akk xk akn xn bk .
Из последнего уравнения находим xk (или
выражаем через остальные неизвестные).
Подставляем в предпоследнее уравнение и
находим xk 1 .
Таким образом найдем все остальные
неизвестные.
24.
Пример.2 x1 3 x2 x3 7,
x1 2 x2 x3 2,
x
2 x3 3.
1
25.
Прямой ход1 11 2
3 1 7 2 23 3 13 71 7 17 7
22 1 2
1 2
03 0 7 7 3 3 11 11
2 1
0 2 3 07 0 3 3 5 5 1 1
2
3 1 7
0 7
3 11
0
0 26 26
26.
23 1 7
3 11
0 7
0
0 26 26
Обратный ход
26 x3 26 x3 1
7 x 2 3 x3 11 7 x 2 3 11 x2 2
2 x1 3 x 2 x3 7 2 x1 6 1 7 x1 1















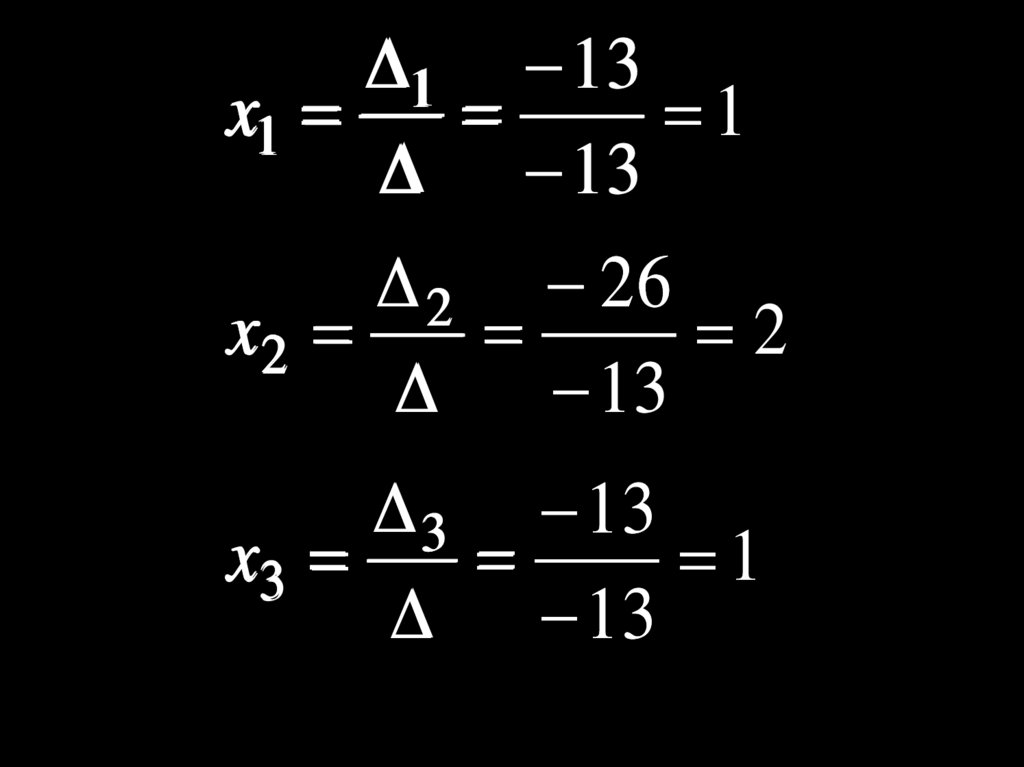







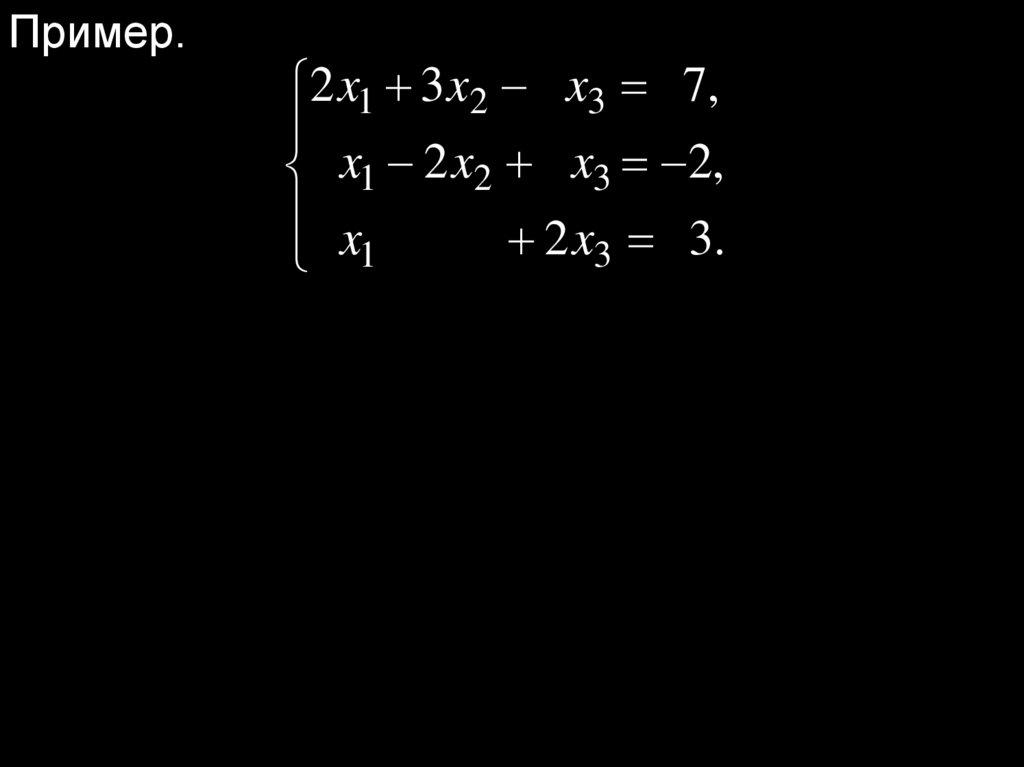


 Математика
Математика








