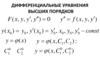§4. Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах

1.

§ 4. Дифференциальные уравнения высших порядков. Задача
Коши. Понятие о краевых задачах. Уравнения, допускающие
понижение порядка
Дифференциальное уравнение п-го порядка в общем случае имеет
вид:
(4.1)
F x, y, y ,..., y n 0 ,
где F – непрерывная функция всех своих аргументов. ДУ n-го порядка,
разрешенное относительно y(n), имеет вид
(4.2)
y n f x, y, y ,..., y n 1
Общим решением ДУ п-го порядка называют функцию
y ( x, C1 , C 2 ,...,C n ) ,
(4.3)
которая при любых значениях параметров C1 , C2 ,...,Cn является
решением этого уравнения. Уравнение
( x, y , C1 , C2 ,...,Cn ) 0 ,
(4.4)
определяющее общее решение как неявную функцию, называется общим
интегралом ДУ п-го порядка.

2.

Задачей Коши для ДУ (4.2) называется задача нахождения решения
y x , удовлетворяющего заданным начальным условиям
y ( x0 ) y0 , y ( x0 ) y0 ,..., y ( n 1) ( x0 ) y0( n 1) .
(4.5)
Если известно общее решение (4.3) дифференциального уравнения
(4.2), то для решения задачи Коши постоянные C1 , C2 ,...,Cn
определяются из системы уравнений
y 0 ( x 0 , C1 , C 2 ,...,C n ) ,
y 0 ( x 0 , C1 , C 2 ,...,C n ) ,
…
y 0 n 1 n 1 ( x 0 , C1 , C 2 ,...,C n ) .
В случае дифференциального уравнения второго порядка частное
решение можно найти заданием краевых условий, когда задаются
значения функции в двух разных точках y x x y1 и y x x y 2 . В этом
1
2
случае лишь найдя общее решение ДУ можно установить, имеет ли
поставленная задача решения и сколько таких решений.

3.

Уравнения, допускающие понижение порядка.
1) Уравнение имеет вид
y n f x .
Это уравнение решается последовательным интегрированием правой и
левой части уравнения.
Пример. Найти общее решение уравнения третьего порядка
y 48 x 6 .
Последовательно интегрируя правую и левую часть уравнения,
находим
y 48 x 6 dx 24 x 2 6 x C1 ,
y 24 x 2 6 x C1 dx 8 x 3 3 x 2 C1 x C 2 ,
x2
y 8 x 3x C1 x C 2 dx 2 x x C1
C2 x C3 .
2
3
2
4
3

4.

2) Уравнение не содержит искомой функции и ее производных до
порядка (k – 1) включительно:
(4.6)
F ( x, y ( k ) , y ( k 1) ,..., y ( n ) ) 0 .
В этом случае замена p y k позволяет понизить порядок уравнения до
n – k, так как после замены уравнение примет вид
F ( x, p, p ,..., p ( n k ) ) 0 .
Из этого уравнения можно найти p p x, C1 , C2 ,...,Cn k , а затем найти у
с помощью интегрирования k раз функции p p x, C1 , C2 ,...,Cn k .

5.

Пример. Решить уравнение y y 2 .
Замена y p (x) и y p дает уравнение 1-го порядка
относительно р:
p p 2 ,
Откуда, последовательно интегрируя, получим
1
dp
1
1
dp
2 dp
, y
,
p , 2 dx , 2 dx , x C1 , p
p
dx
x C1
x C1
p
p
dx
y y dx
ln( x C1 ) C 2 ,
x C1
y y dx ln( x C1 ) C 2 dx
x
ln( x C1 )dx C 2 x x ln( x C1 )
dx C 2 x
x C1
x ln( x C1 ) x C1 ln( x C1 ) C 2 x C3
C3 C 4 x ( x C1 ) ln( x C1 ) .

6.

3) Уравнение не содержит независимой переменной:
(4.7)
F y, y ,..., y n 0 .
Порядок такого уравнения понижается на единицу заменой y p . При
этом производные функции f x по х нужно выразить через
производные р по у:
dy
d 2 y dp dp dy
p ( x),
p y p pp y и т.д.
2
dx
dx dy dx
dx
Пример. Решить уравнение y 2 yy .
Пусть y p, y pp y , тогда получим
pp y 2 yp .
Частное решение имеет вид p 0 , т.е. y 0, y C.
dp
2 y , откуда имеем
Если p 0, после сокращения на р имеем
dy
dy
dy
1
y
2
2
dp
2
ydy
,
p
y
C
,
y
C
,
dx
,
arctg
x C2 ,
1
1 2
C1
C1
dx
y C1
y C1 tg C1 x C 2 .

7.

§ 5. Линейные однородные дифференциальные уравнения
высших порядков
Линейным дифференциальным уравнением (ЛДУ) п-го порядка
называют уравнение, линейное относительно неизвестной функции и ее
производных и имеющее вид:
a 0 ( x ) y ( n ) a1 ( x ) y ( n 1) ... a n 1 ( x ) y a n ( x ) y f ( x ) ,
(5.1)
где a 0 ( x ), a1 ( x ),..., a n 1 ( x ), a n ( x ) и f(x) – функции аргумента x.
Если f ( x) 0 , уравнение называют линейным неоднородным
дифференциальным уравнением (ЛНДУ) или линейным дифференциальным
уравнением с правой частью.
f ( x) 0 , уравнение называют линейным однородным
Если
дифференциальным уравнением (ЛОДУ) или линейным дифференциальным
уравнением без правой части. Оно имеет вид:
a 0 ( x ) y ( n ) a1 ( x ) y ( n 1) ... a n 1 ( x ) y a n ( x ) y 0 .
(5.2)
Функции y1 x , y2 x ,…, yn x называют линейно зависимыми в
некотором интервале a, b , если существуют такие числа 1 , 2 ,…, n , не
все равные нулю, что
1 y1 2 y2 ... n yn 0
(5.3)
на рассматриваемом интервале.

8.

Пример. Функции 1, x, x², …, xn линейно независимы на любом
интервале, так как равенство
1 2 x 3 x 2 ... n 1 x n 0
справедливо только при всех i 0 . Иначе в левой части равенства стоял
бы многочлен степени не выше п, который может обращаться в нуль не
более, чем в п точках рассматриваемого интервала.
Если равенство (5.3) справедливо только при всех i 0 , то
функции y1 x , y2 x ,…, yn x называют линейно независимыми на
интервале a, b .
Общее решение однородного уравнения (5.2) имеет вид
(5.4)
y C1 y1 x C 2 y 2 x ... C n y n x ,
где y1 x , y 2 x , ..., y n x – линейно независимые частные решения
уравнения (5.3), C1 , C 2 , ..., C n – произвольные постоянные.
Фундаментальной системой решений называют любые п линейно
независимых решений однородного линейного уравнения (5.2).
Следовательно, общее решение уравнения (5.2) является линейной
комбинацией любой его фундаментальной системы решений.

9.

Пусть коэффициенты a 0 ( x ), a1 ( x ),..., a n 1 ( x ), a n ( x ) уравнения (5.2) –
константы. Тогда частные решения y1 x , y 2 x , ..., y n x имеют вид
y e kx , где k – константа. В этом случае
y ( p ) k p e kx и, после
подстановки в уравнение (5.2) выражения y e kx и соответствующих
производных, получаем:
a0 k n e kx a1k n 1e kx ... an e kx 0 .
После сокращения на ekx получим характеристическое уравнение
(5.5)
a0 k n a1k n 1 ... an 1k an 0 .
Числа k, являющиеся его решениями, при подстановке в функцию
выражения y e kx дают частные решения дифференциального
уравнения. Здесь возможны следующие случаи.

10.

1) Корни характеристического уравнения различные и
действительные.
В этом случае общее решение дифференциального уравнения (5.2)
может быть записано в виде:
y c1e k1x c2 e k2 x ... cn e kn x .
Пример. Найти общее решение уравнения y ( 5) 5 y 4 y 0 .
Характеристическое уравнение имеет вид
k 5 5k 3 4k 0 .
Разложим левую часть на множители:
k ( k 2 4)( k 2 1) 0 .
Следовательно, корни характеристического уравнения имеют вид:
k1 0, k 2 2, k3 2, k 4 1, k5 1 .
Поэтому общее решение заданного уравнения имеет вид:
y c1 c2 e 2 x c3e 2 x c4 e x c5 e x .