Похожие презентации:
ДУ высших порядков. Задача Коши для уравнения порядка n
1. Математика Часть 2
УГТУ-УПИ2007 г.
2.
Лекция 12ДУ высших порядков.
1. Задача Коши для уравнения порядка n.
Требуется найти решение ДУ n-го порядка
n
n 1
y f ( x , y , y ',..., y ),
удовлетворяющего заданным начальным условиям:
y x0 y0 ,
x0 y0 ,
y
..........
y n 1 x y n 1 .
0
0
3.
Теорема Коши (теорема существования иединственности решения ДУ)
Т
Если в уравнении
n
n 1
y f ( x , y , y ', ..., y
),
n 1
) и её частные
функция f ( x , y , y ',..., y
производные по аргументам
y , y ',..., y
n 1
непрерывны в области, содержащей точку
x x 0 , y y0 , y
y0
, ..., y
n 1
y0
n 1
,
4.
то существует единственное решение y y ( x )этого уравнения, удовлетворяющее начальным
условиям:
y x 0 y0 , y
x0 y0 ,..., y
n 1
x 0 y0
n 1
.
Частное решение ДУ (решение задачи Коши)
может быть найдено из общего решения по
заданным начальным условиям, из которых
получают систему уравнений для определения
постоянных c 0 , c 0 , ..., c 0 :
1
2
n
5.
y x0 , c10 , ..., cn0 y0 ,0
0
,
y x0 , c1 , ..., cn y0
......
n 1
n 1
0
0
y
x
,
c
,
...,
c
y
0
1
n
0
Решение задачи Коши ДУ n-го порядка имеет
вид:
y x , c , ..., c .
0
1
0
n
6.
2.Дифференциальные уравнения,
допускающие понижение порядка.
. y
n
f x . (правая часть зависит только от х)
Общее решение получается путем n-кратного
интегрирования:
y
y
n
( n 1)
y
n 1
,
f ( x )dx c1 ;
7.
y( n 2)
(
f ( x )dx )dx c1 x c2 , ...,
n 1
n 2
c1 x
c2 x
y
... f ( x )dx ...dx
... cn .
n 1 ! n 2 !
Пример.
Найти частное решение ДУ
y
e
2x
,
удовлетворяющее начальным условиям:
y 0 1, y
0 1, y
0 0.
8.
Решение.1 2x
y
e dx e c1 ,
2
1 2x
y
e c1 x c2 ,
4
2
1 2x
x
y e c1 c2 x c3 .
8
2
2x
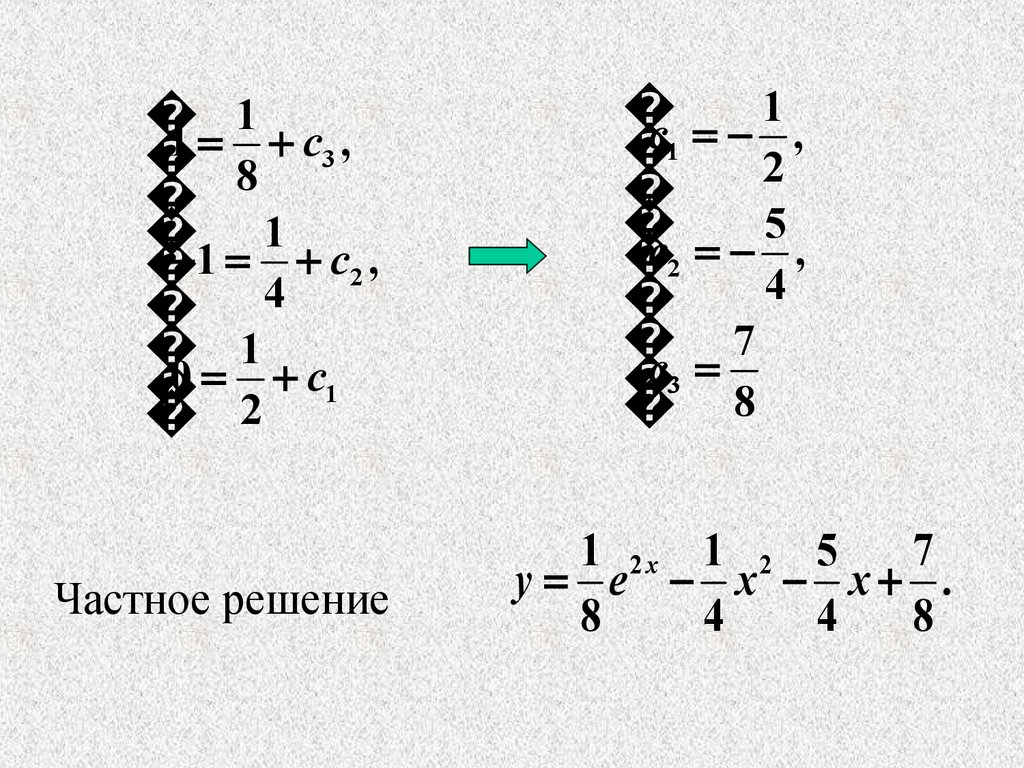
Из начальных условий определяем постоянные
c1 , c2 , c3 :
9.
11 c3 ,
8
1
1 c2 ,
4
1
0 c1
2
Частное решение
1
c1 ,
2
5
c2 ,
4
7
c3
8
1 2x 1 2 5
7
y e x x .
8
4
4
8
10.
kn
. F x , y , ..., y
0.
(нет y и её производных до (k-1)-го порядка)
Подстановка y
k
P x понижает порядок
уравнения на k :
1) F ( x , p, p ', ..., p
( n k )
) 0
если P P ( x , C1 , ..., C n k ) - общее решение 1),
то 2) y
(k )
P ( x , C1 , C 2 , ..., C n k )
- ДУ типа I.
11.
Пример .y
x 1 0.
Найти общее решение ДУ xy
Решение.
Уравнение не содержит
y, y
.
dP
y
.
Подстановка y
P x
dx
P 1
P
1 - линейное для функции P x
x x
Подстановка P x u x v x
c1
x
P 1 ,
2
x
c1
x
y
1
,
2
x
12.
2c
x
x
1
y
dx c2
x c1 ln x c2 ,
2 1 x
4
x
y
dx c3 ,
x c1 ln x c2
4
2
3
2
x
x
y
c1 x ln x 1 c2 x c3 .
12 2
13.
. F y , y, y
, ..., y
Подстановка
y
dP y
dx
n
0. (Уравнение не содержит х).
y
P y
dP dy
dP
P
dy dx
dy
y
P
P,
y
y
...
понижает порядок уравнения на 1.
14.
Пример .Найти общее решение ДУ
Решение.
y
0.
2 yy
Уравнение явно не содержит
Подстановка
y
P y
P 2 yP
P 0
2
2
x.
dP
y
P.
dy
P 2 yP
0
Возможна потеря решения
dy
P y
0, y const .
dx
15.
2 yPP,
dP
dy
,
P
2y
1
ln P ln y ln c1 ,
2
dy c1
,
dx
y
3
2
2
y c1 x c2 .
3
P c1 y
ydy c1 dx ,
1
2
c1
y
,
16.
d( n 1)
V.
G( x , y, y
,..., y ) 0
dx
(Левая часть уравнения представлена в виде полной
производной по x от некоторой функции.)
Интегрирование понижает порядок уравнения
на единицу.
Пример.
xy
y
x 1 0, y ?
Решение.
2
x
xy
x
2
2
x
xy
x c1 ,
2
17.
c1x
y
1
- ДУ типа I.
2
x
2
x
y
x c1 ln x c2 ,
4
3
2
x x
y c1 x ln x 1 c2 x c3 .
12 2
18.
3. Линейные дифференциальныеуравнения.
Линейным называется ДУ, содержащее
функцию y и её производные в первой
степени.
19.
Линейное дифференциальное уравнениеназывается неоднородным (НЛДУ) если оно
имеет вид:
n
y a1 y
где
n 1
... an y f x ,
ai ( i 1, 2, ..., n), f x 0
непрерывные функции от x или постоянные.
Линейное ДУ называется однородным (ОЛДУ),
если f x 0 .
20.
Рассмотрим ОЛДУ второго порядка:y
a1 y
a2 y 0.
Пусть y1 y1 x , y2 y2 x - частные решения ДУ.
Два решения ДУ y1 , y2
называются
линейно независимыми, если их линейная
комбинация c1 y1 c2 y2 0 лишь в случае
когда c1 c2 0.
( y1 , y2- линейно зависимы y2 cy1 . )
21.
Пример.y1 e x , y2 3e x линейно зависимы,
x
y1 e , y2 e
x
линейно независимы.
22.
Для функцийy1 x , y2 x определитель
W y1 , y2
y1
y2
y1 y2
y1
y2
y1 y2
называется определителем Вронского.
Т. Если функции
на
a, b ,
то
y1 , y2 линейно зависимы
W y1 , y2 0, x a , b .
Доказательство:
y2 y1 y2 y1
,
23.
W y1 , y2Т.
y1
y2
y1
y1
y1
y1
0.
y1 y2 y1 y1
y1 y1
Если функции y1 , y2 линейно независимы
на a , b , то W y1 , y2 0, x a , b .
Доказательство:
Допустим
W y1 , y2 0, y1 y2
y1
y2 0.
y1 y2
y1
y2
y2
0
Для y1 0 :
0
2
y1
y1
y2
const . Противоречие. W 0.
y1
24.
y1 , y2 - линейно независимыечастные решения ОЛДУ второго порядка
y
a1 y
a2 y 0,
то общее решение этого
уравнения равно их линейной комбинации:
Т. Если
y c1 y1 c2 y2 ,
c1 , c2 - произвольные постоянные.
Доказательство:
a1 y2
a2 y2 0.
y1
a1 y1
a2 y1 0, y2
Подставим
y c1 y1 c2 y2 в исходное уравнение:
a1 c1 y1 c2 y2
a2 c1 y1 c2 y2
c1 y1 c2 y2
25.
c1 y1a1 y1
a2 y1 c2 y2
a1 y2
a2 y2 0,
y c1 y1 c2 y2 решение ОЛДУ.
Докажем, что при любых начальных условиях
y x 0 y0 , y
x0 y0
можно подобрать c1 , c2 так , чтобы решение
удовлетворяло этим начальным условиям.
Пусть
y1 x0 y10 , y2 x0 y20 ,
y1
x0 y10 , y2 x0 y20 .
26.
Подставим начальные условия вy0 c1 y10 c2 y20
y0 c1 y10 c2 y20
т.к.
y1 , y2
W x0
y c1 y1 c2 y2 :
y10
y20
0,
y10 y20
- линейно независимы.
Система уравнений имеет единственное решение
c1 , c2 .
27.
Любые два линейно независимых частныхрешения y1 и y2 ОЛДУ второго порядка
называются фундаментальной системой
решений этого уравнения.
Общее решение является линейной комбинацией
фундаментальной системы решений:
y c1 y1 c2 y2 .
28.
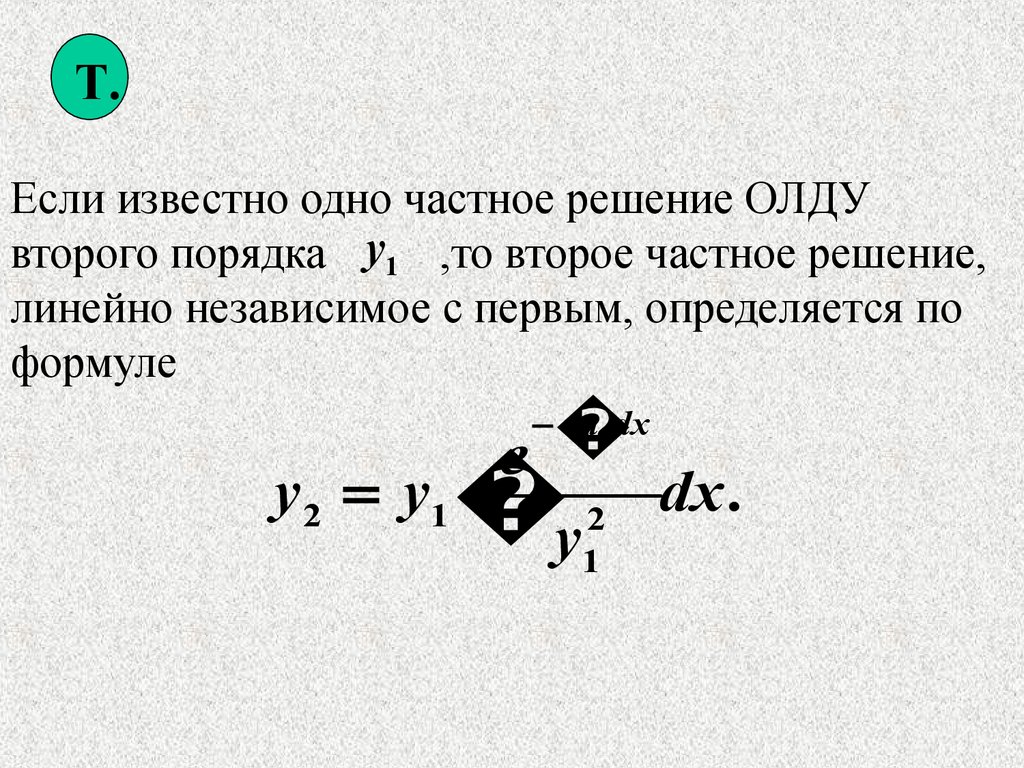
Т.Если известно одно частное решение ОЛДУ
второго порядка y1 ,то второе частное решение,
линейно независимое с первым, определяется по
формуле
e
y2 y1 2 dx .
y1
a1dx










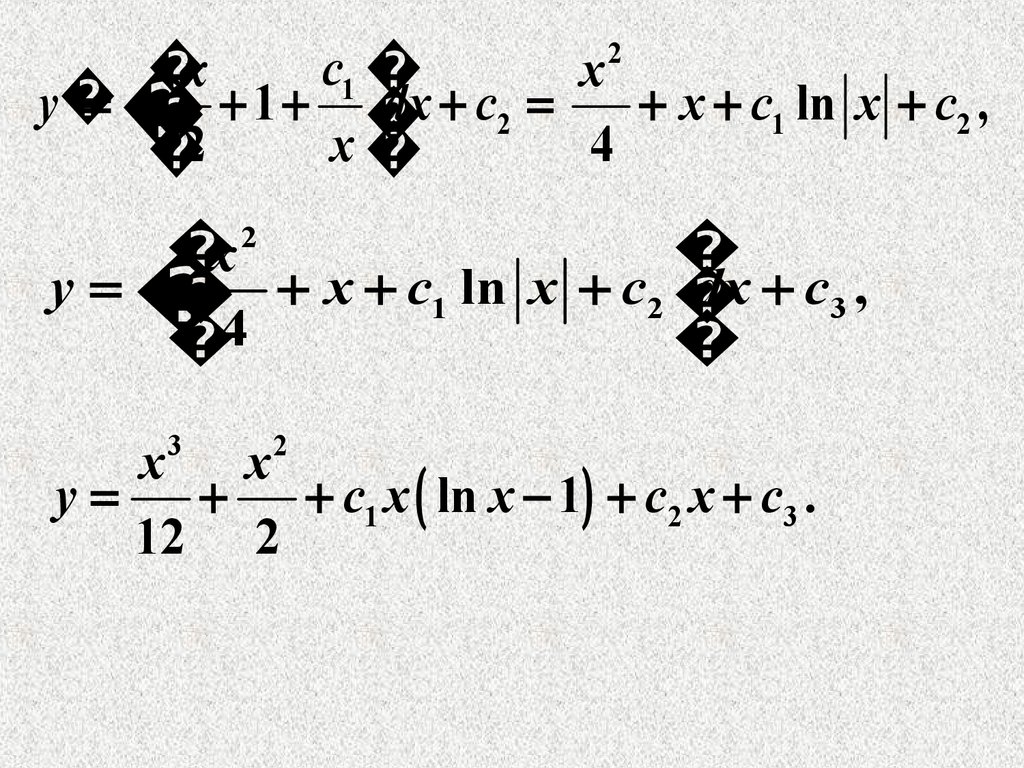




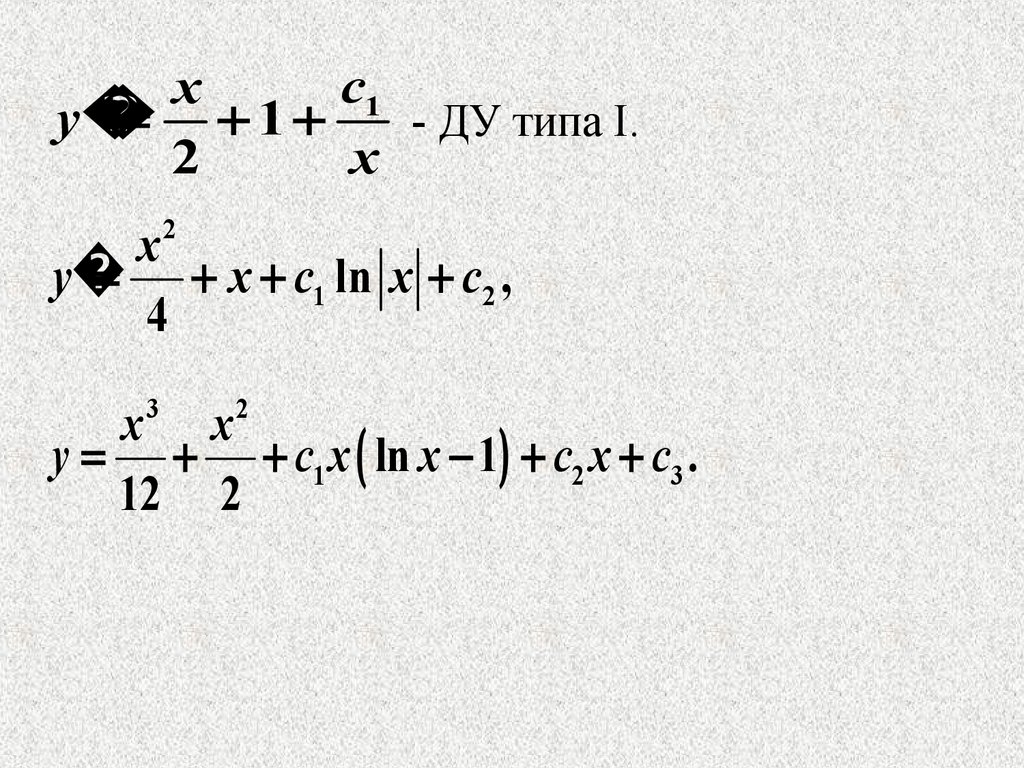



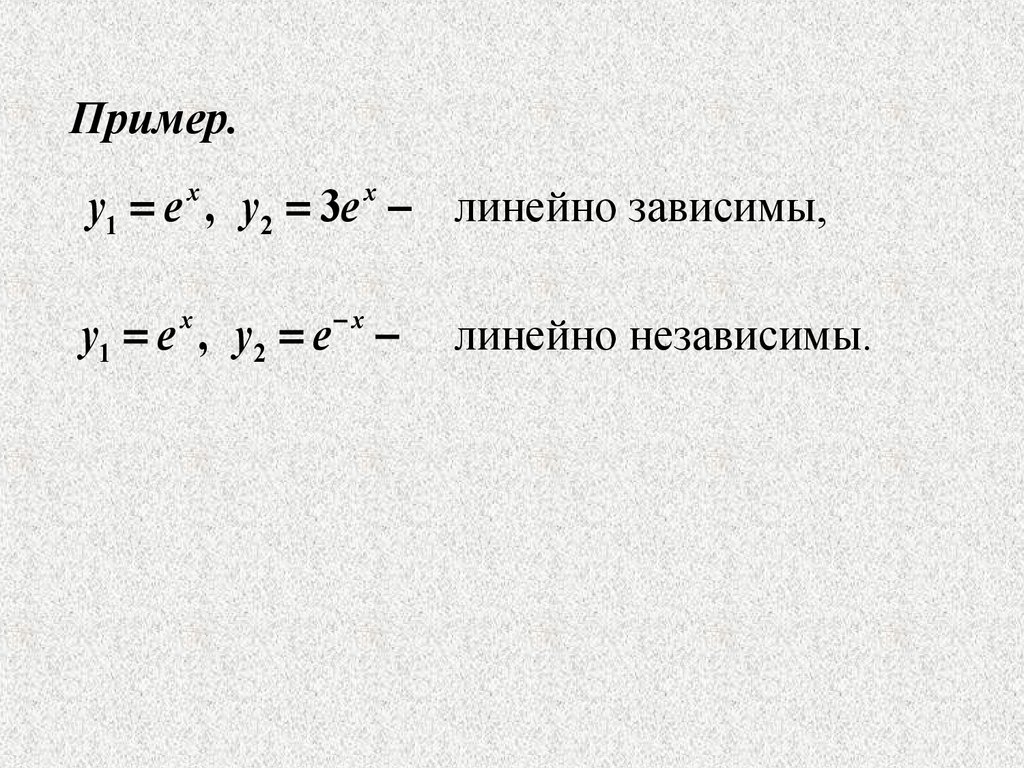






 Математика
Математика








