Треугольник. Геометрия. 7 класс

1.

ТРЕУГОЛЬНИК
Геометрия
7 класс

2.

3.

Треугольником называется фигура,
которая состоит из трёх точек, не
лежащих на одной прямой, и трёх
отрезков, соединяющих эти точки.
А
В
С
Точки А, В и С называются вершинами .
Отрезки АВ, ВС и СА называются сторонами
треугольника .

4.

5.

7 класс
ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ
В ТРЕУГОЛЬНИКЕ

6.

Медиана треугольника
СМ = МВ
Отрезок,
соединяющий
вершину треугольника
с серединой
противоположной
стороны, называется
медианой
треугольника.
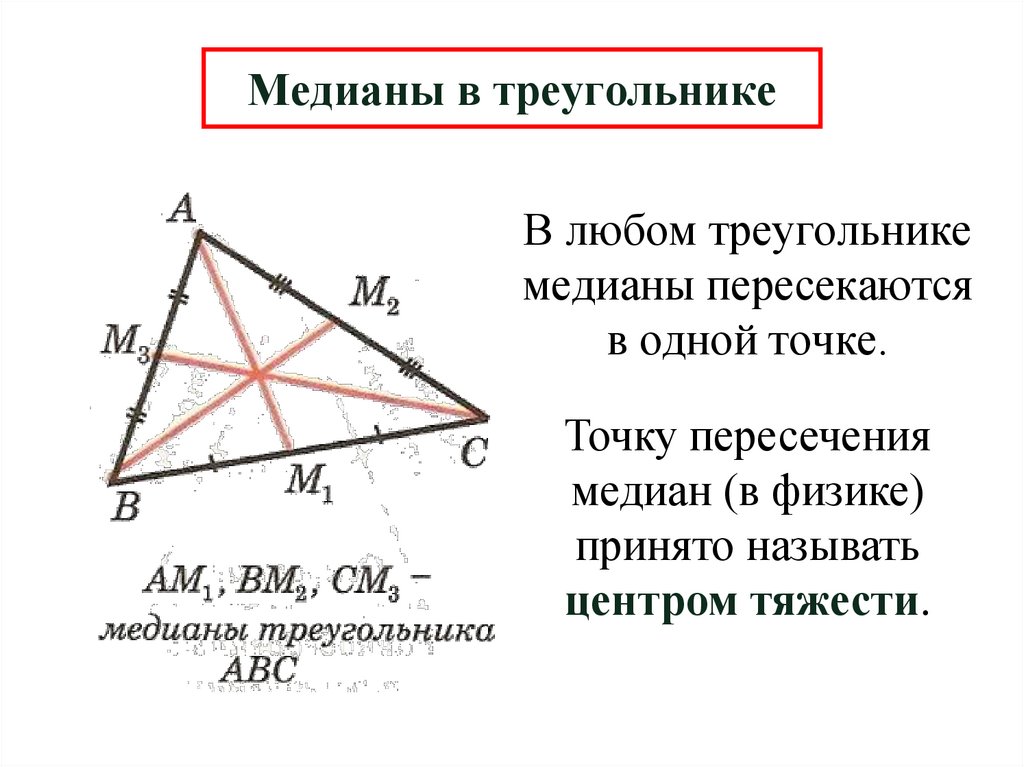
АМ – медиана треугольника

7.

Медианы в треугольнике
В любом треугольнике
медианы пересекаются
в одной точке.
Точку пересечения
медиан (в физике)
принято называть
центром тяжести.

8.

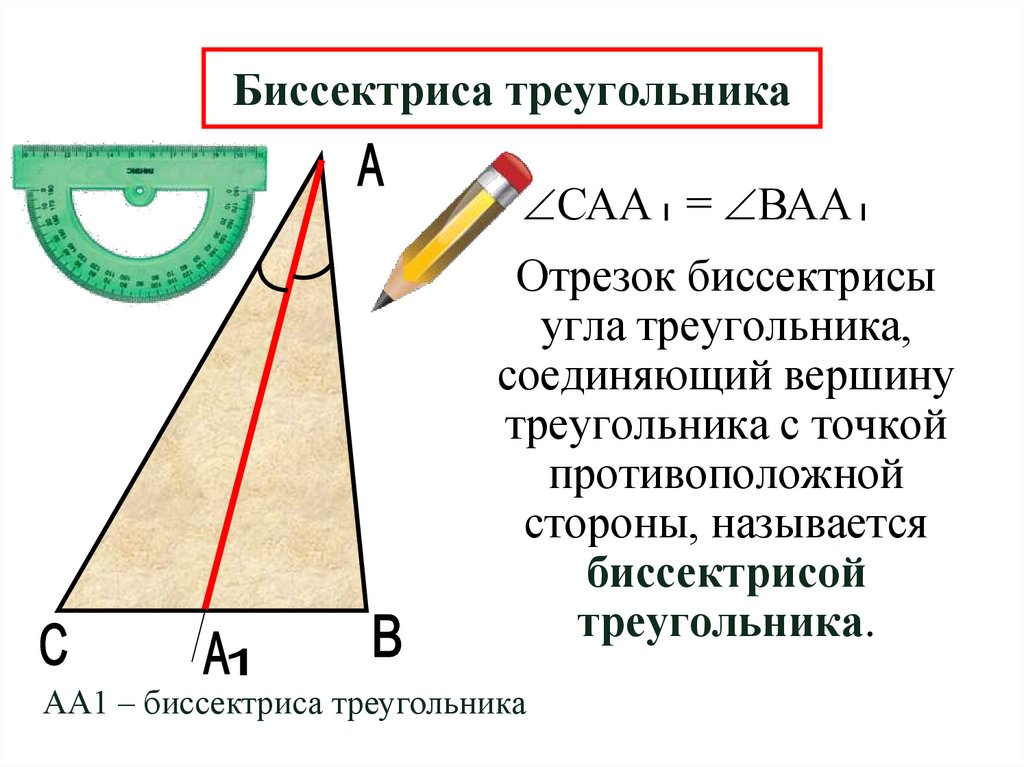
Биссектриса треугольника
САА = ВАА
Отрезок биссектрисы
угла треугольника,
соединяющий вершину
треугольника с точкой
противоположной
стороны, называется
биссектрисой
треугольника.
АА1 – биссектриса треугольника

9.

Биссектрисы в треугольнике
В любом треугольнике
биссектрисы
пересекаются в одной
точке.
Точка пересечения
биссектрис
треугольника есть
центр вписанной в
треугольник
окружности.

10.

Перпендикуляр к прямой
А а, АН а
Отрезок АН называется
перпендикуляром,
проведенным из точки
А к прямой а, если
прямые АН и а
перпендикулярны.

11.

Теорема о перпендикуляре
Из точки, не лежащей
на прямой, можно
провести
перпендикуляр к этой
прямой, и притом
только один.

12.

Высота треугольника
АН СВ
Перпендикуляр,
проведенный из
вершины
треугольника к
прямой, содержащей
противоположную
сторону, называется
высотой
треугольника.
АН – высота треугольника

13.

Высоты в треугольнике

14.

Высоты в треугольнике
В любом треугольнике
высоты или их
продолжения
пересекаются в одной
точке.
Точку пересечения
высот называют
ортоцентром.

15.

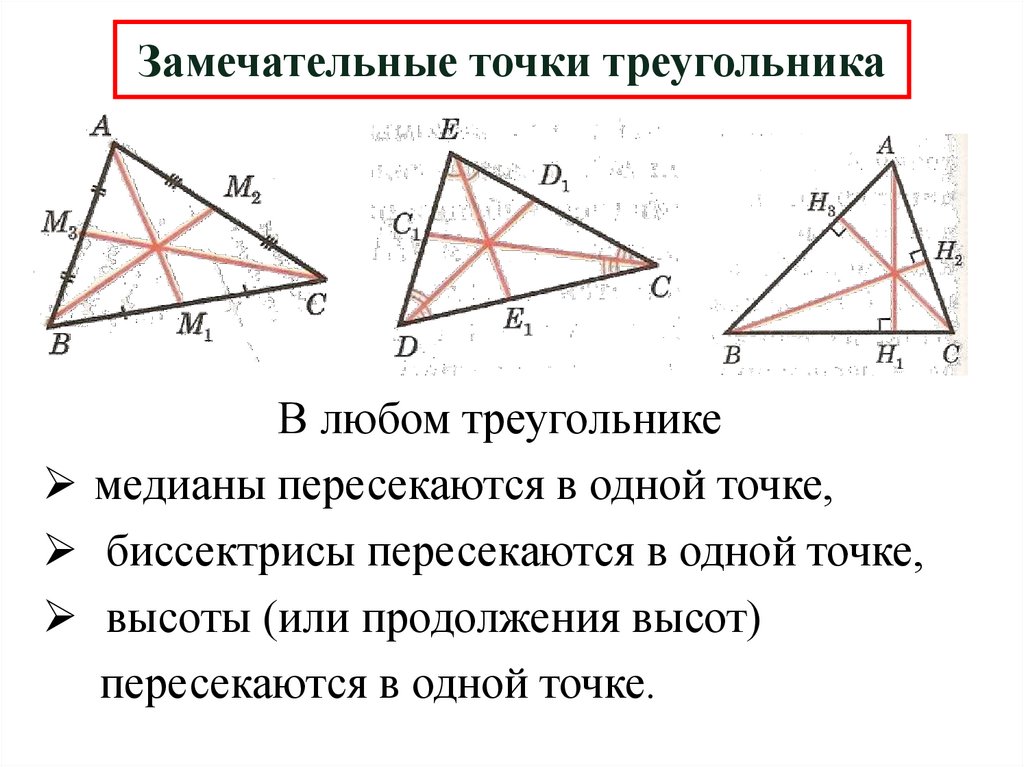
Замечательные точки треугольника
В любом треугольнике
медианы пересекаются в одной точке,
биссектрисы пересекаются в одной точке,
высоты (или продолжения высот)
пересекаются в одной точке.

16.

2)
60 60
6)
1)
8)
3)
7)
4)
9)
11)
5)
13)
10)
12)
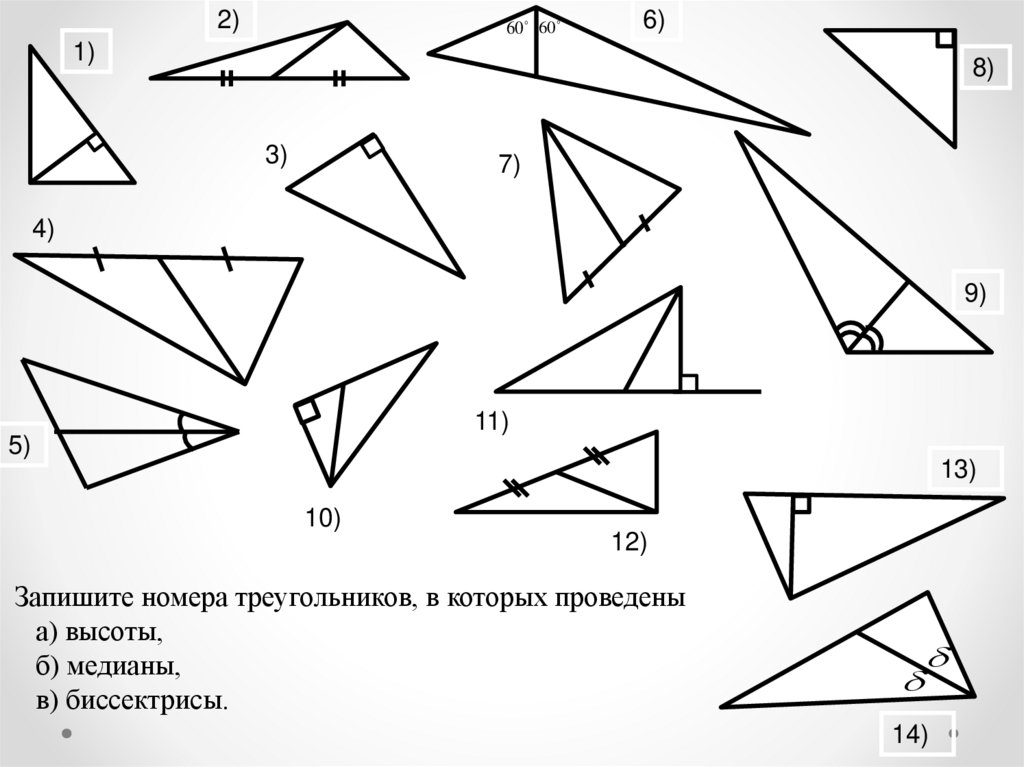
Запишите номера треугольников, в которых проведены
а) высоты,
б) медианы,
в) биссектрисы.
14)

17.

ПРИЗНАКИ
РАВЕНСТВА
ФИГУР

18.

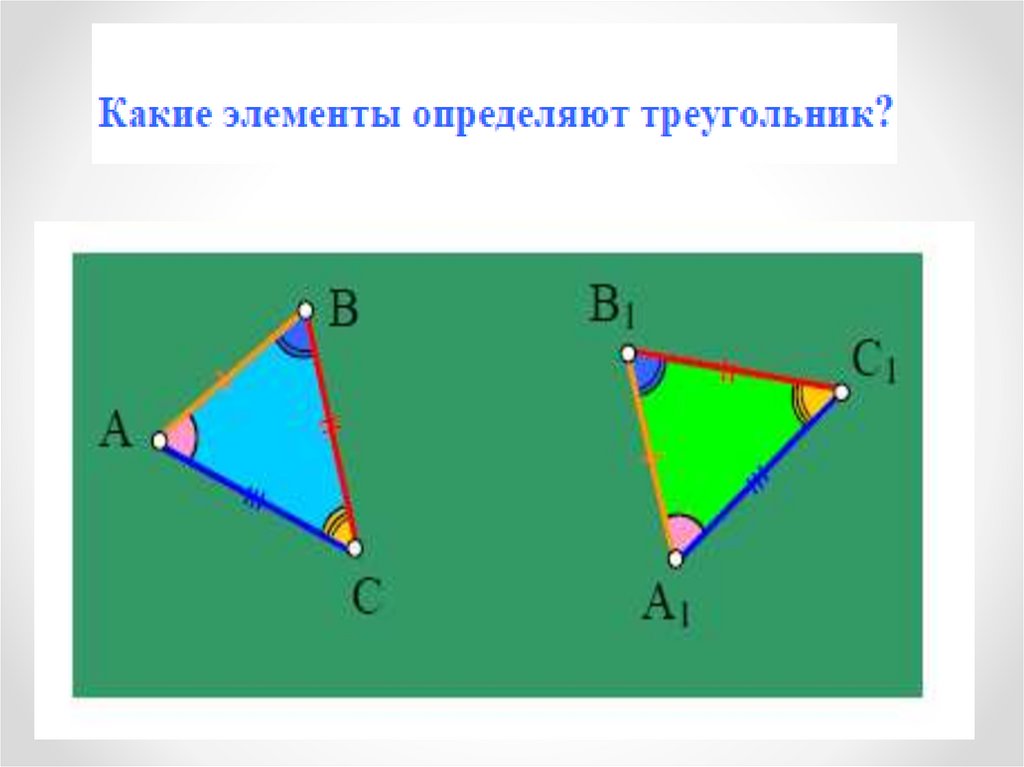
Что такое признаки
равенства?

19.

20.

21.

ПРИЗНАКИ

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

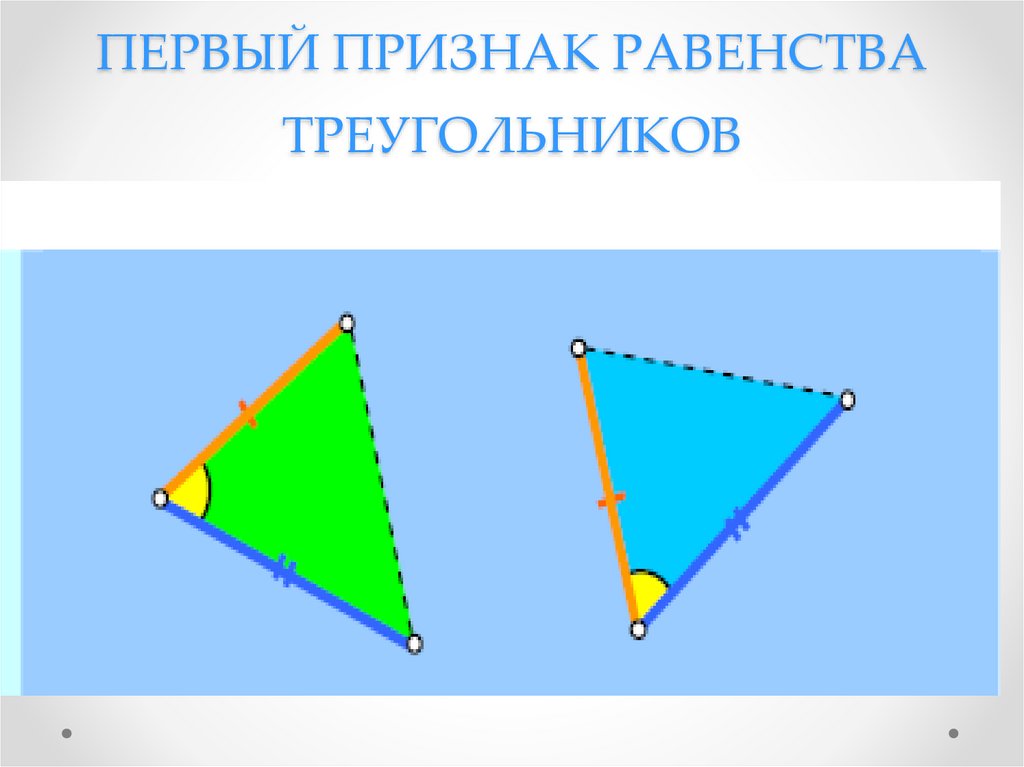
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА
ТРЕУГОЛЬНИКОВ

37.

ТЕОРЕМА
I признак равенства треугольников
по двум сторонам и углу между ними.
Если две стороны и угол между ними одного
треугольника соответственно равны двум
сторонам и углу между ними другого треугольника,
то такие треугольники равны.
ЗАКЛЮЧЕНИЕ
37
У
С
Л
О
В
И
Е

38.

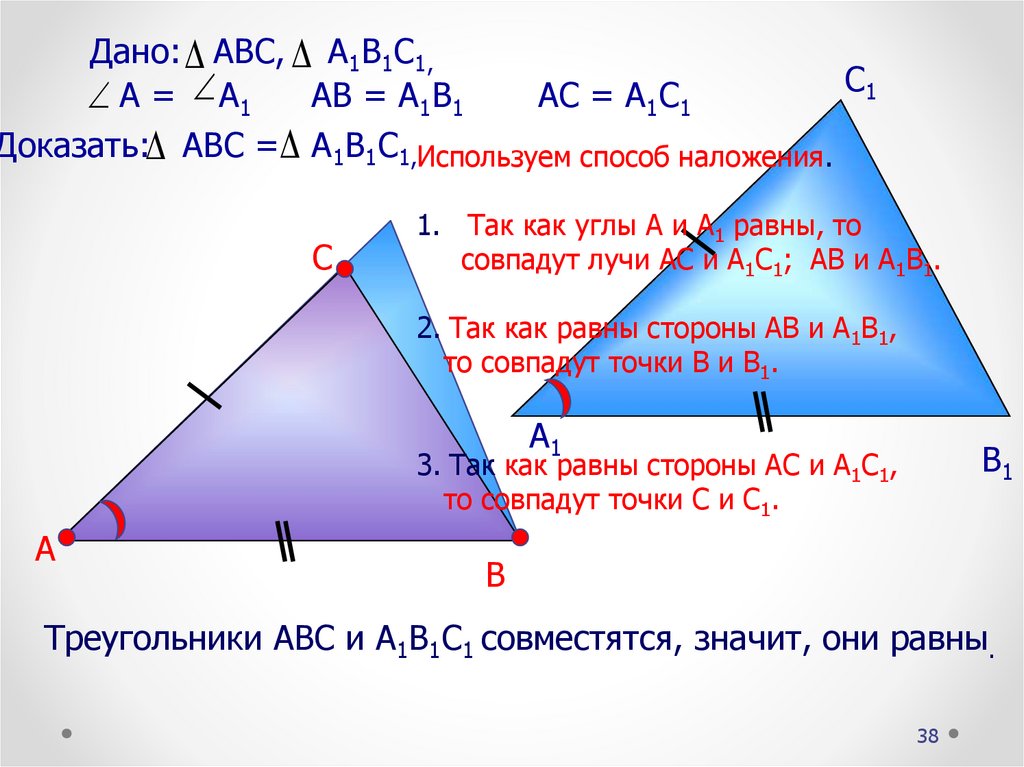
Дано: АВС, А1В1С1,
С1
АВ = А1В1
АС = А1С1
А = А1
Доказать: АВС = А1В1С1,Используем способ наложения.
С
1. Так как углы А и А1 равны, то
совпадут лучи АС и А1С1; АВ и А1В1.
2. Так как равны стороны АВ и А1В1,
то совпадут точки В и В1.
А1
В1
3. Так как равны стороны АС и А1С1,
то совпадут точки С и С1.
А
В
Треугольники АВС и А1В1С1 совместятся, значит, они равны.
38

39.

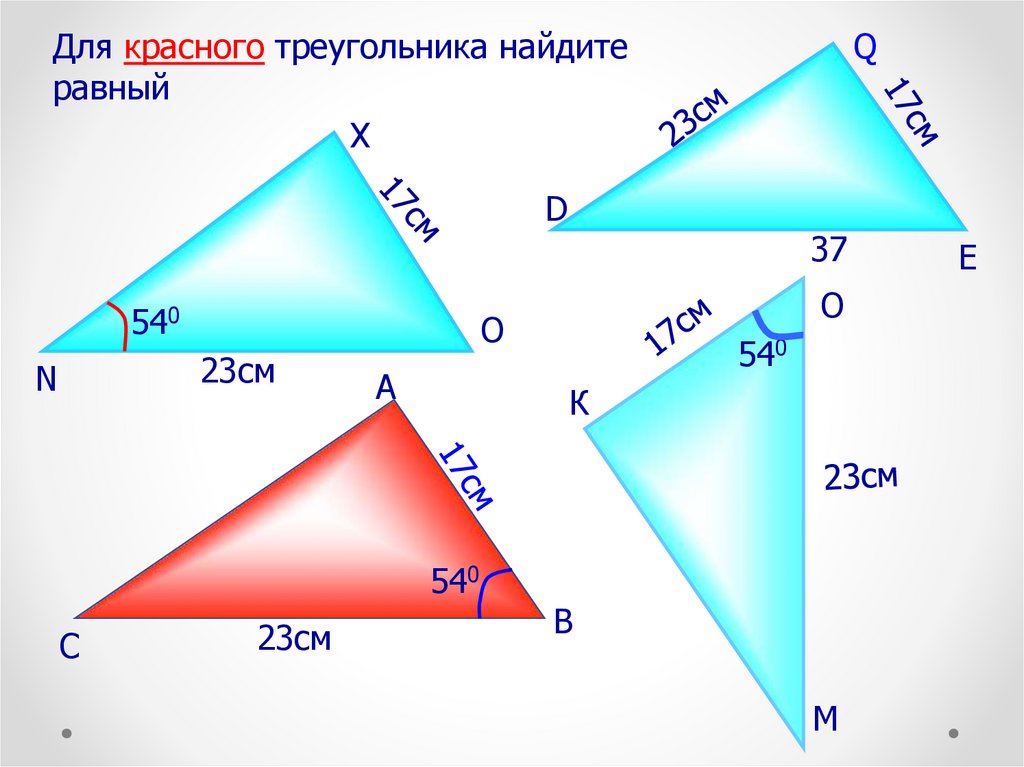
Для красного треугольника найдите
равный
X
Q
D
540
23см
N
С
О
O
А
540
К
540
23см
37
В
М
E

40.

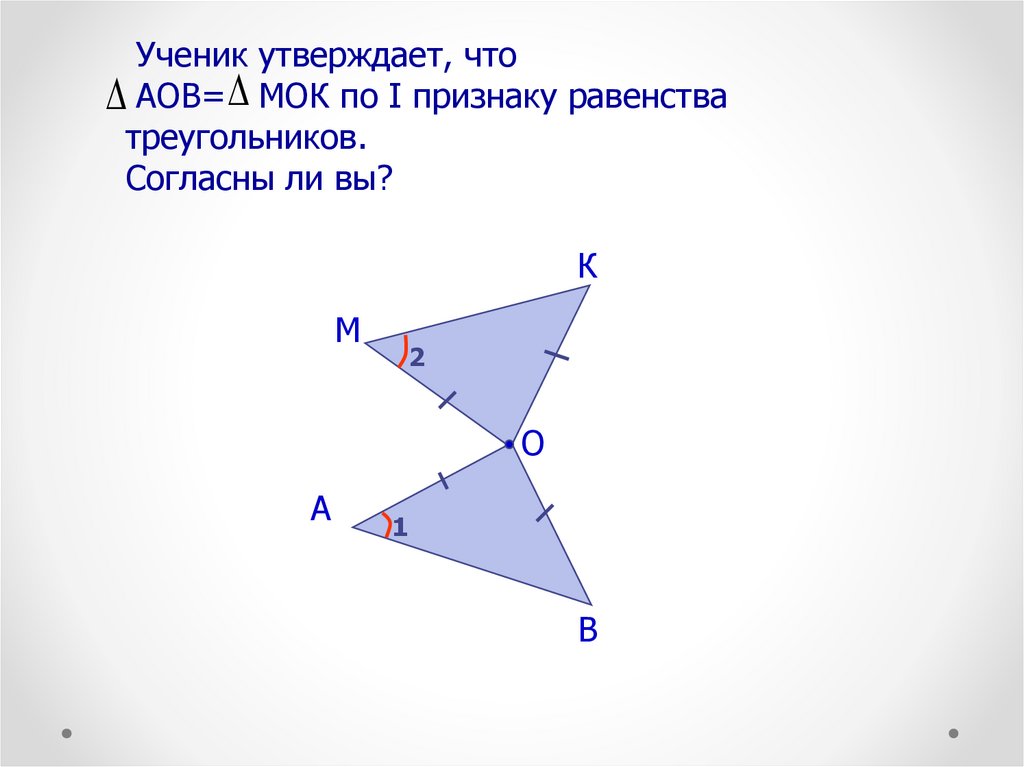
Ученик утверждает, что
АОВ= МОК по I признаку равенства
треугольников.
Согласны ли вы?
К
М
2
О
А
1
В

41.

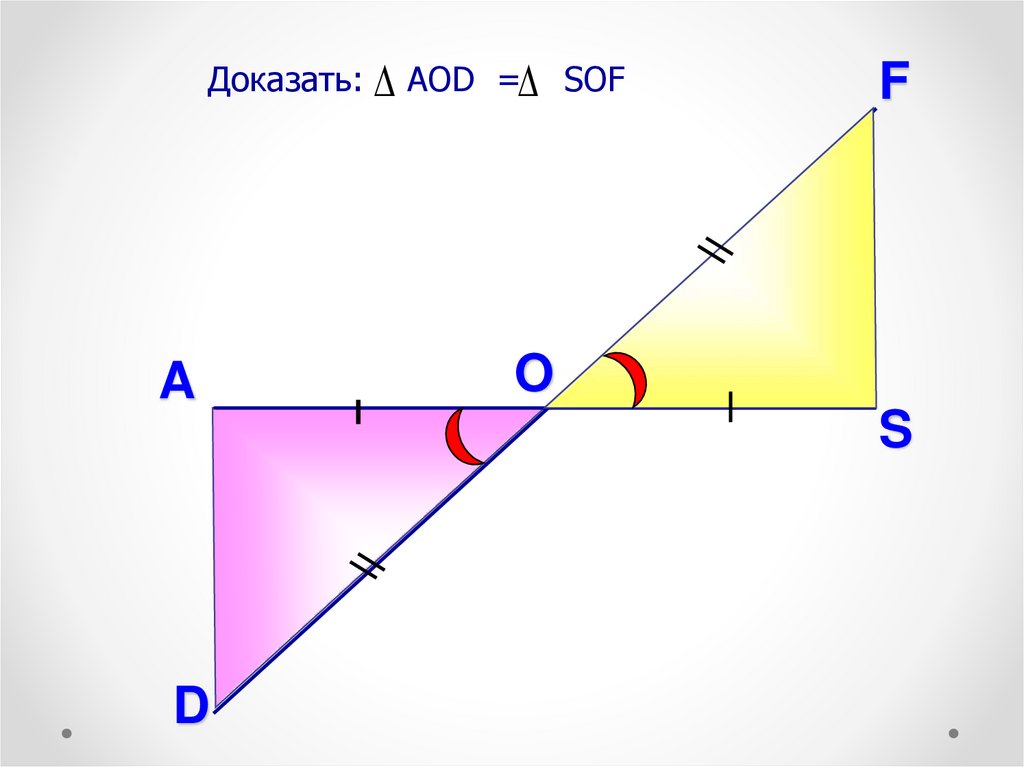
Доказать: AOD = SOF
A
F
O
S
D

42.

На рисунке АА1 = СС1, ВС = В1С1, ВС АС,
Доказать: АСВ = А1С1В1
В
А
C
А1
В1С1 А1С1
В1
С1
42