Методы решения дифференциальных уравнений в частных производных

1. Методы решения дифференциальных уравнений в частных производных

Введение

2. Дифференциальное уравнение в частных производных

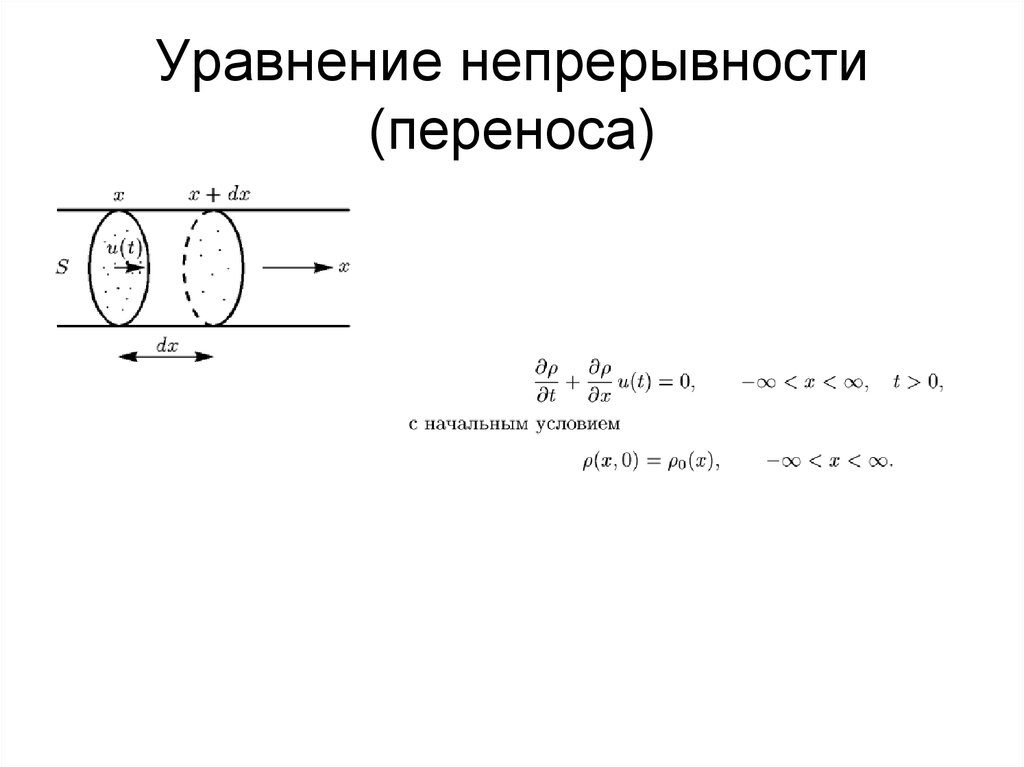
Системы ДУЧП

3. Уравнение непрерывности (переноса)

4. Уравнение непрерывности (переноса)

5. Уравнение переноса

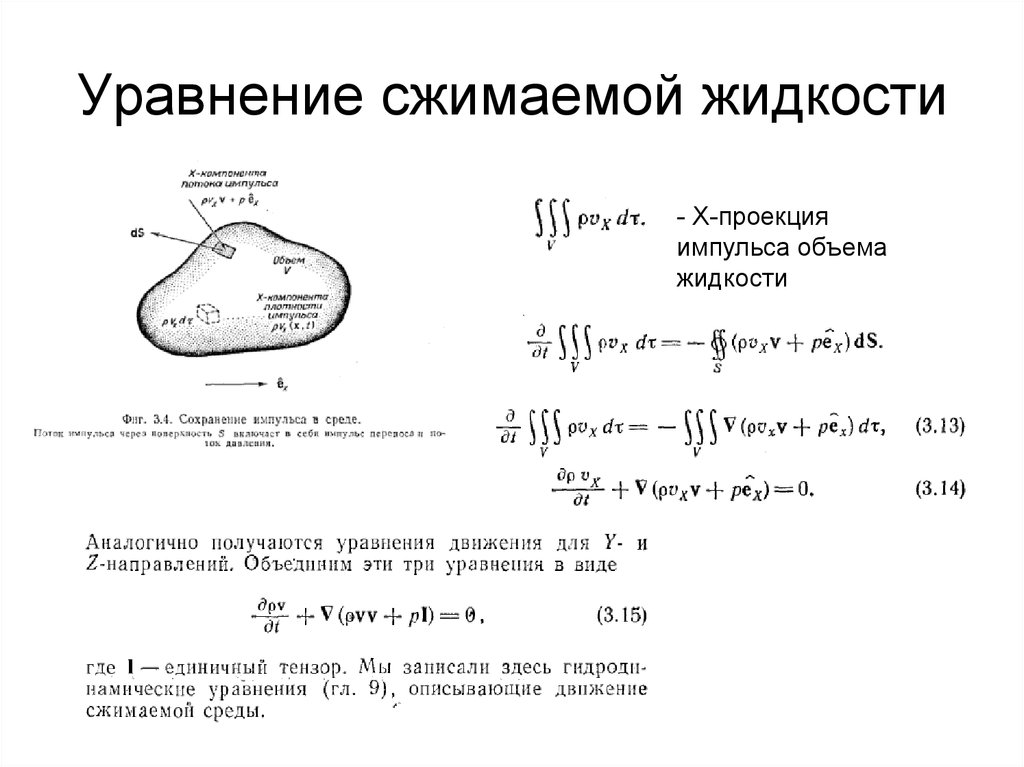
6. Уравнение сжимаемой жидкости

- Х-проекция
импульса объема
жидкости

7. Уравнения классической гидродинамики

уравнение состояния

8. Уравнение теплопроводности

9. Уравнения электромагнетизма

10. Консервативные ДУ

11. Уравнение диффузии

12. Волновое уравнение

13. Уравнение Пуассона и Лапласа

14. Классификация ДУЧП 2-го порядка

15. Аппроксимация производных конечными разностями

16. Граничные и начальные условия

17. Аппроксимация производных конечными разностями

18. Аппроксимация 1-го порядка точности

19. Аппроксимация 1-го порядка точности

20. Центральная аппроксимация 2-го порядка

21. Центральная аппроксимация 2-ой производной

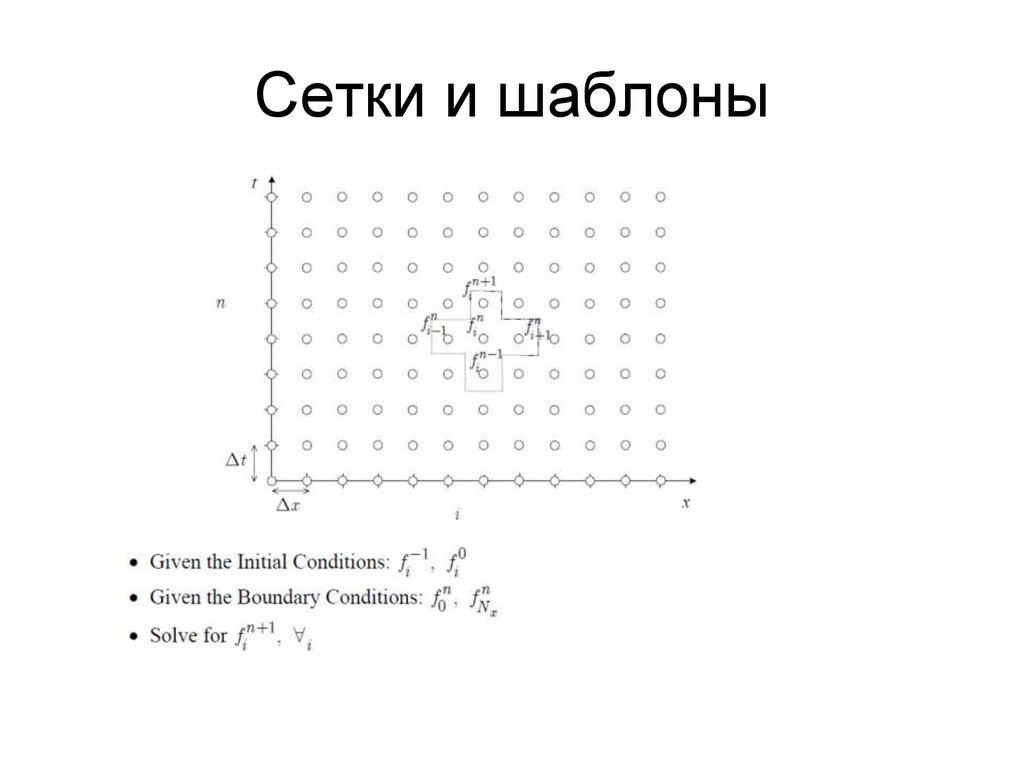
Центральная аппроксимация 2ой производной

22. Сетки и шаблоны

23. Точность аппроксимации

24. Явные и неявные схемы

25. Методы составления схем

• Метод разностной аппроксимации
• Интегро-интерполяционный метод
(законы сохранения)
• Метод неопределенных коэффициентов

26. Сходимость

27. Анализ устойчивости по методу Неймана

Исследуется поведение Фурье-мод на
сетке независимо друг от друга.
Требуется устойчивость для каждой из
мод в отдельности.
G – матрица перехода разностной схемы
для выбранной фурье-моды с волновым
числом k.
Устойчивость моды предполагает, что
если ее амплитуда в начальный момент
времени конечна, то она должна
оставаться конечной на всех n шагах.
Тогда
и условие устойчивости -
Разложим моду по
собственным векторам G

28. Анализ устойчивости

• Матрица перехода может меняться по
пространственной и временной сеткам
– условие устойчивости должно
выполняться глобально.

29. Анализ уравнения переноса

30.

31. Схема Лакса

32. Дисперсия и диффузия на сетке

Разностная схема Лакса соответствует ДУ с диффузионным
членом (3), который компенсирует нестабильность,
связанную с тем, что схема не центрирована по времени.

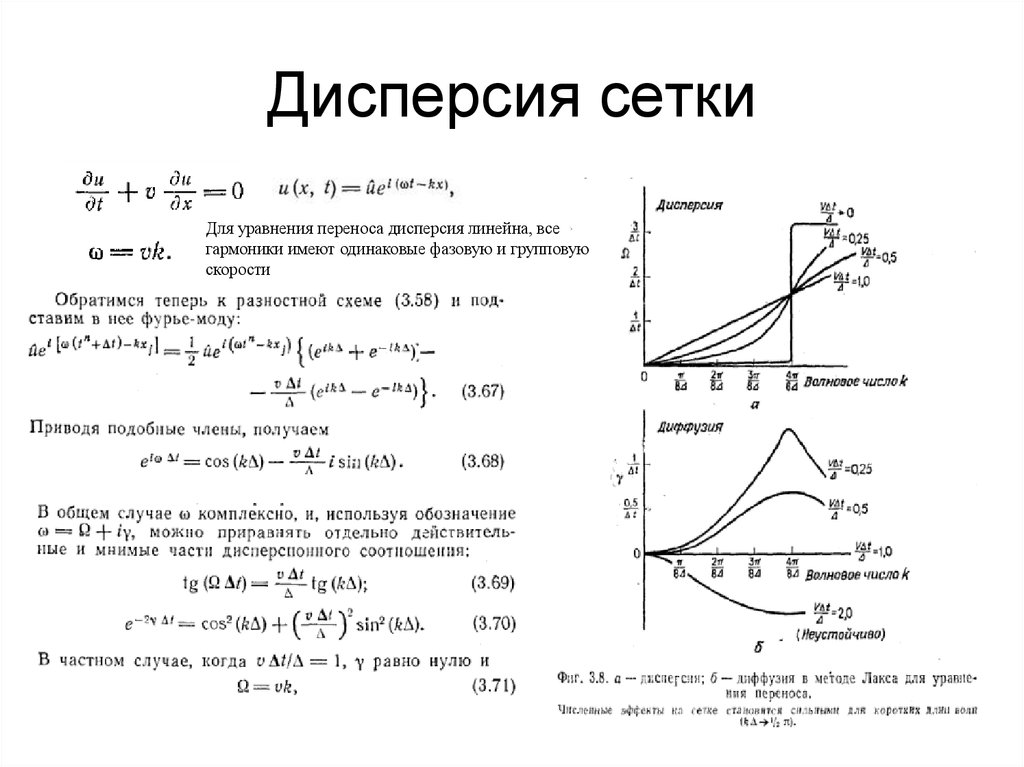
33. Дисперсия сетки

Для уравнения переноса дисперсия линейна, все
гармоники имеют одинаковые фазовую и групповую
скорости

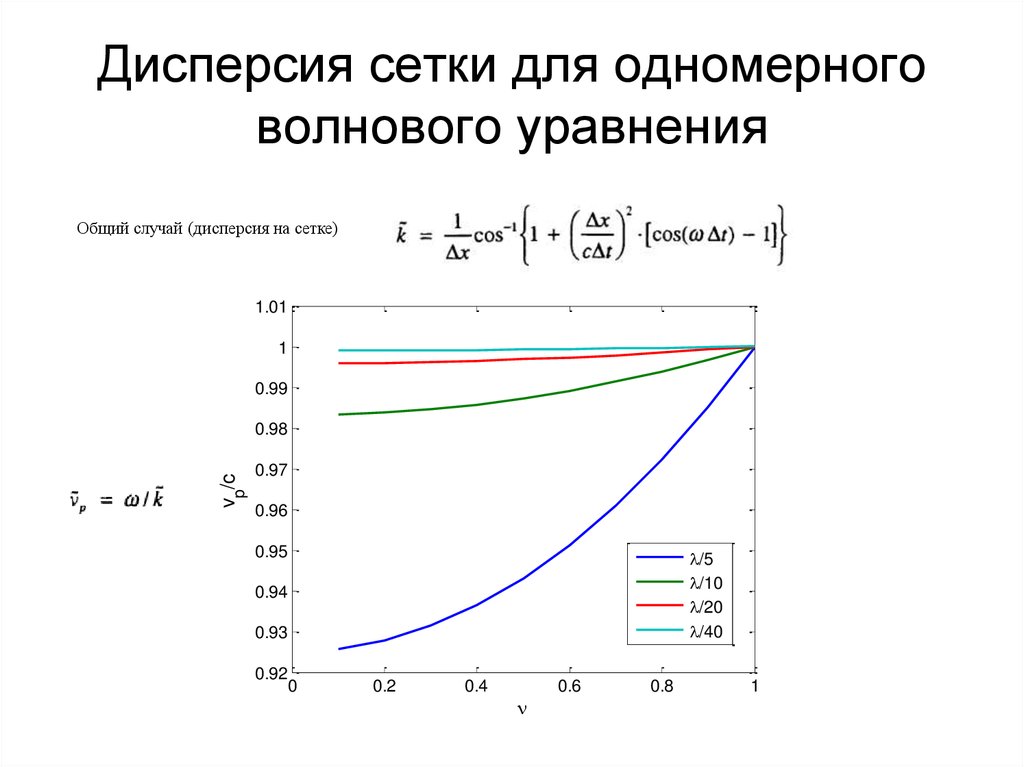
34. Дисперсия сетки для одномерного волнового уравнения

Теперь рассмотрим дисперсию схемы

35. Дисперсия сетки для одномерного волнового уравнения

Рассмотрим случай очень плотной сетки
Рассмотрим случай

36. Дисперсия сетки для одномерного волнового уравнения

Общий случай (дисперсия на сетке)
1.01
1
0.99
vp/c
0.98
0.97
0.96
0.95
/5
/10
/20
/40
0.94
0.93
0.92
0
0.2
0.4
0.6
0.8
1

37. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)

38. Схема 2-го порядка точности по времени и пространству (Лакса-Вендрофа)

39. Устойчивость метода Лакса-Вендрофа

40. Диффузия в схеме Лакса-Вендрофа

41. Условие устойчивости в многомерных задачах гиперболического типа

Метод Лакса
u nj ,l uˆ knx k y e ikx e
ik y
u nj , l 1 uˆ knx k1y e ikx e
ik y
uˆknx k1y uˆknx k y g

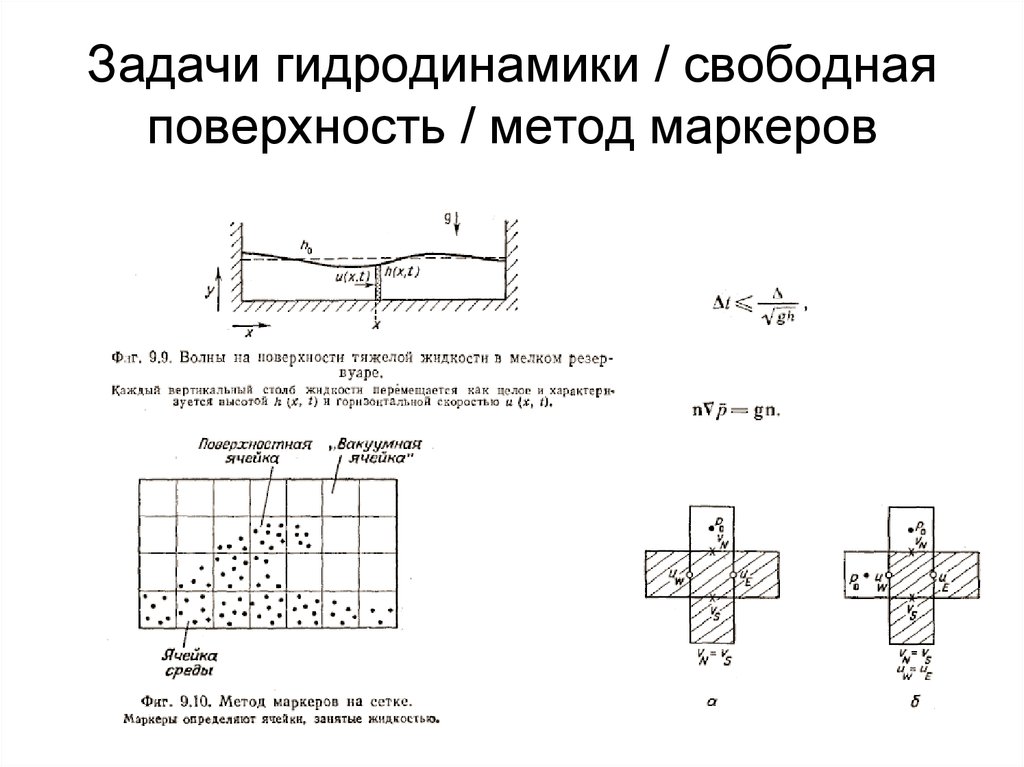
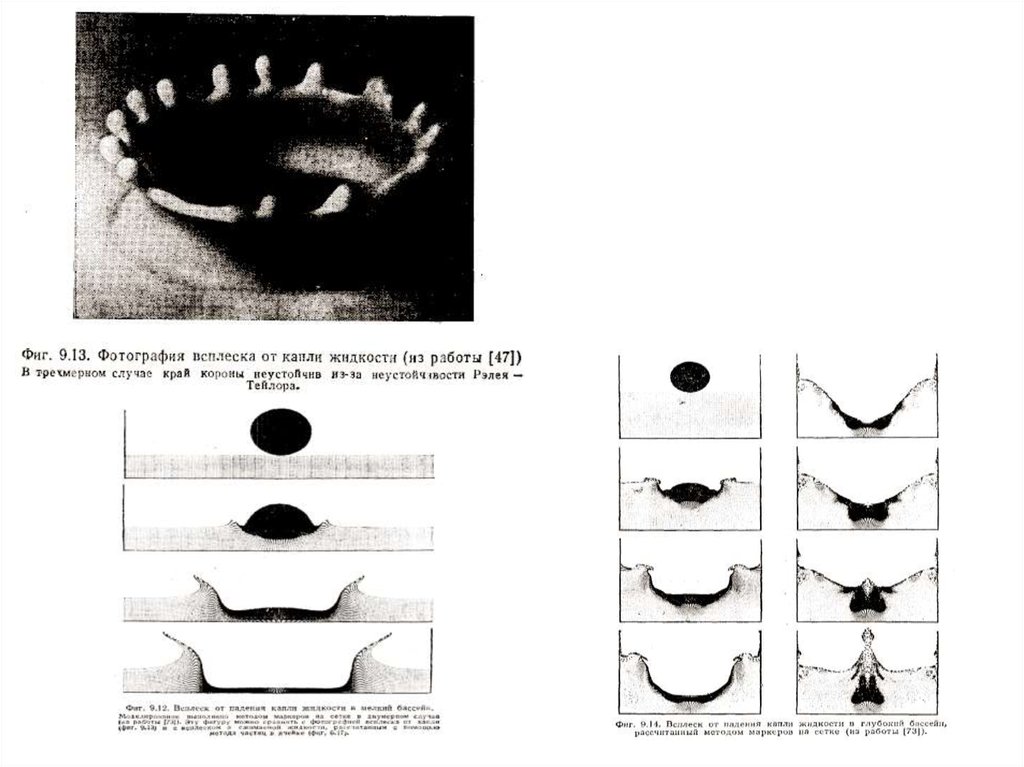
42. Задачи гидродинамики / свободная поверхность / метод маркеров

43.

44.

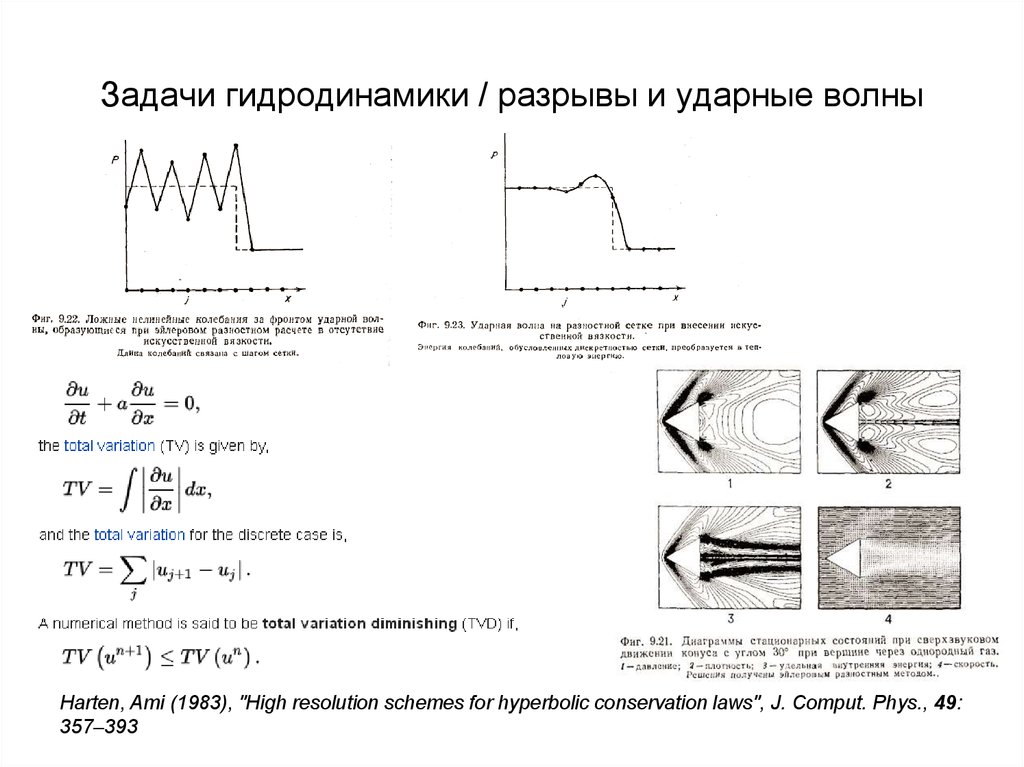
45. Задачи гидродинамики / разрывы и ударные волны

Harten, Ami (1983), "High resolution schemes for hyperbolic conservation laws", J. Comput. Phys., 49:
357–393

46. Консервативные схемы

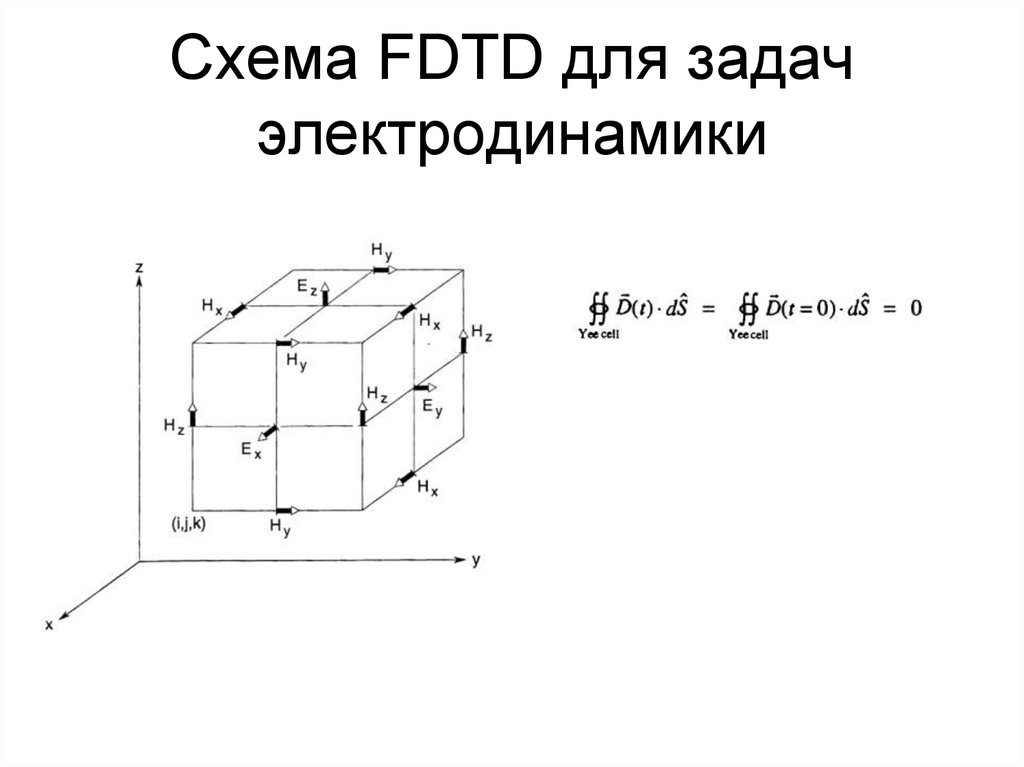
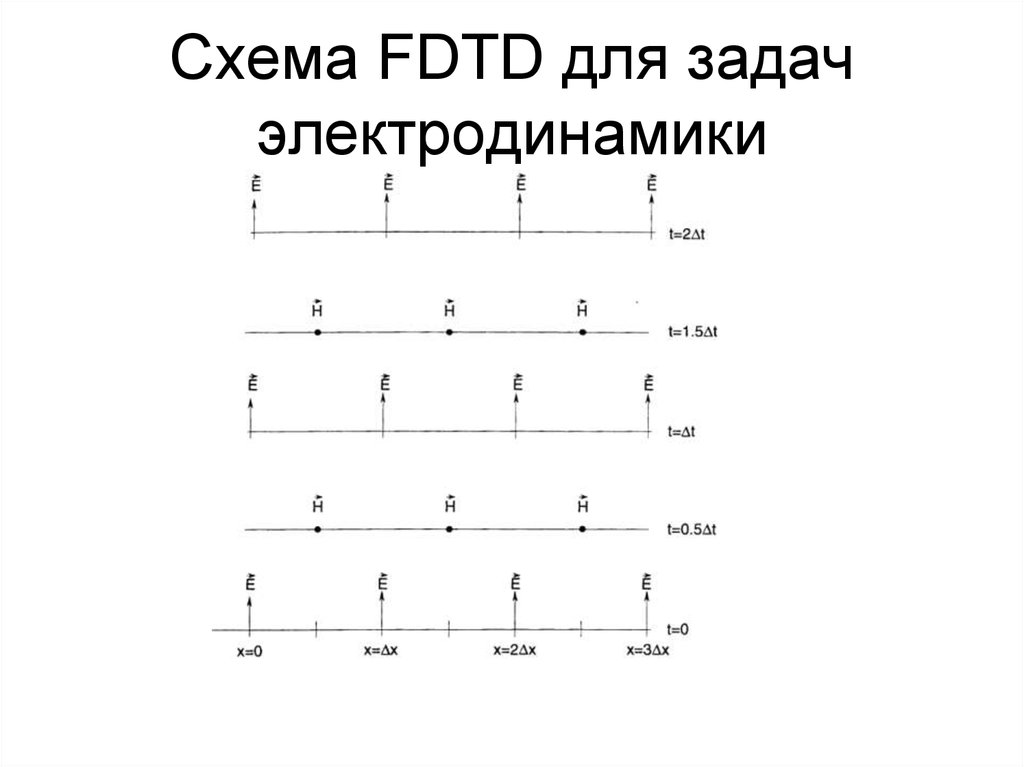
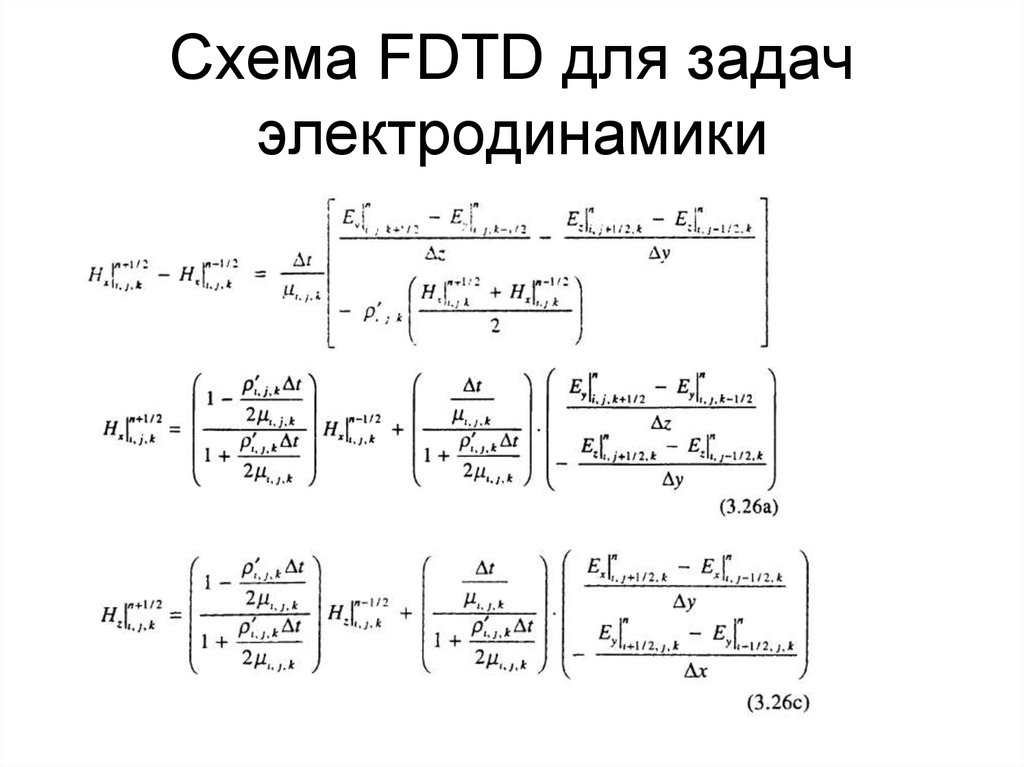
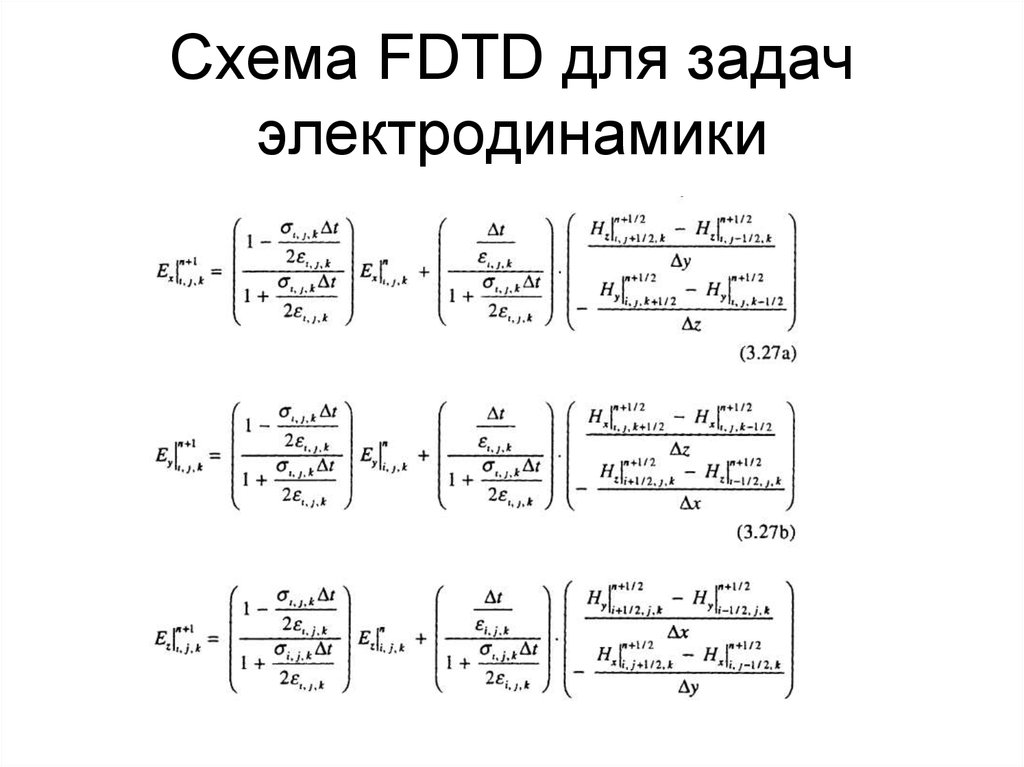
47. Схема FDTD для задач электродинамики

48. Схема FDTD для задач электродинамики

49. Схема FDTD для задач электродинамики

50. Схема FDTD для задач электродинамики

51. Схема FDTD для задач электродинамики

52. Схема FDTD для задач электродинамики

53. Схема FDTD для задач электродинамики

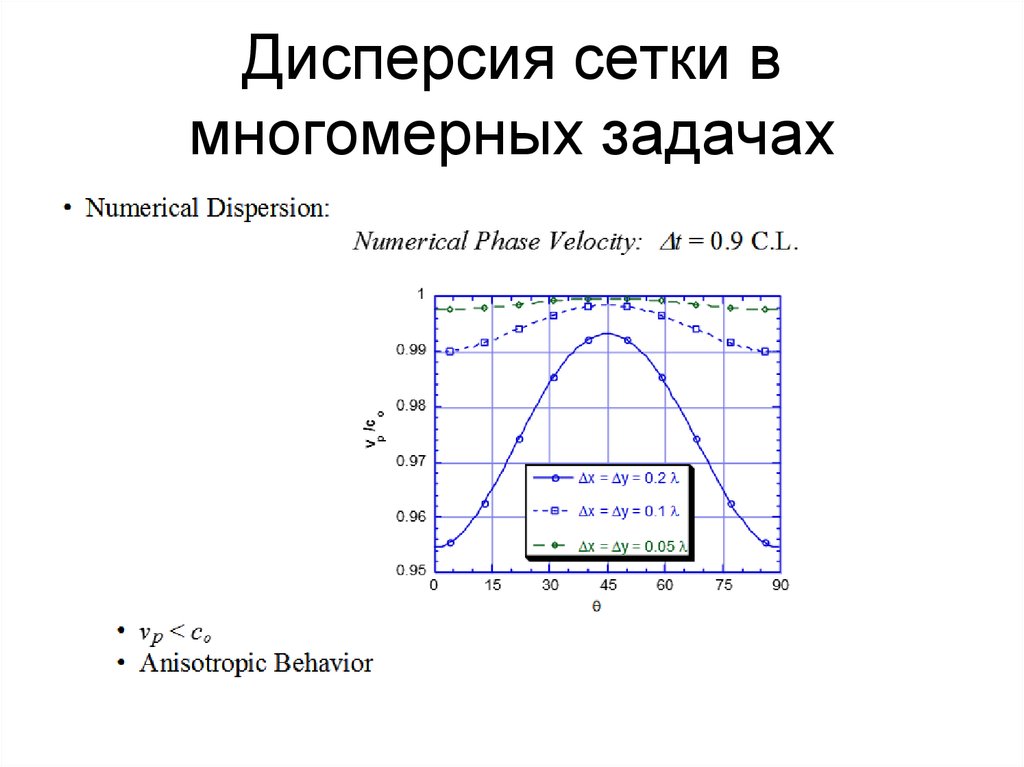
54. Дисперсия сетки в многомерных задачах

55. Устойчивость

Computational Electrodynamics: The Finite-Difference Time-Domain
Method, Third Edition
Allen Taflove