Піраміда

1.

Тема уроку:
”Піраміда”

2. Згадаємо головне

1.Що таке піраміда?
2. Яка піраміда називається правильною?
3.Що називається апофемою?
4.Чому дорівнює площа бічної поверхні
правильної піраміди?
5.Властивості правильної піраміди,
6.Чи може піраміда мати більше вершин, ніж
граней?
7.Чи може число ребер піраміди бути непарним
числом?

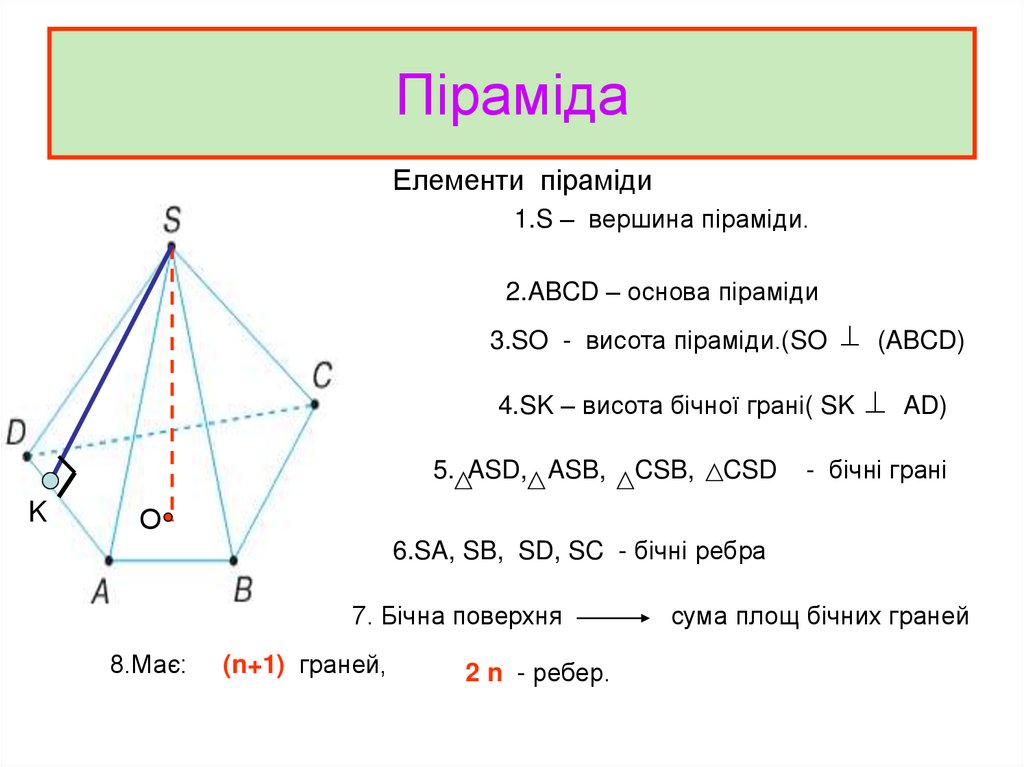
3. Піраміда

Елементи піраміди
1.S – вершина піраміди.
2.ABCD – основа піраміди
3.SO - висота піраміди.(SO (ABCD)
4.SK – висота бічної грані( SK AD)
5. ASD, ASB,
CSD
- бічні грані
О
K
CSB,
6.SA, SB, SD, SC - бічні ребра
7. Бічна поверхня
8.Має:
(n+1) граней,
2 n - ребер.
сума площ бічних граней

4.

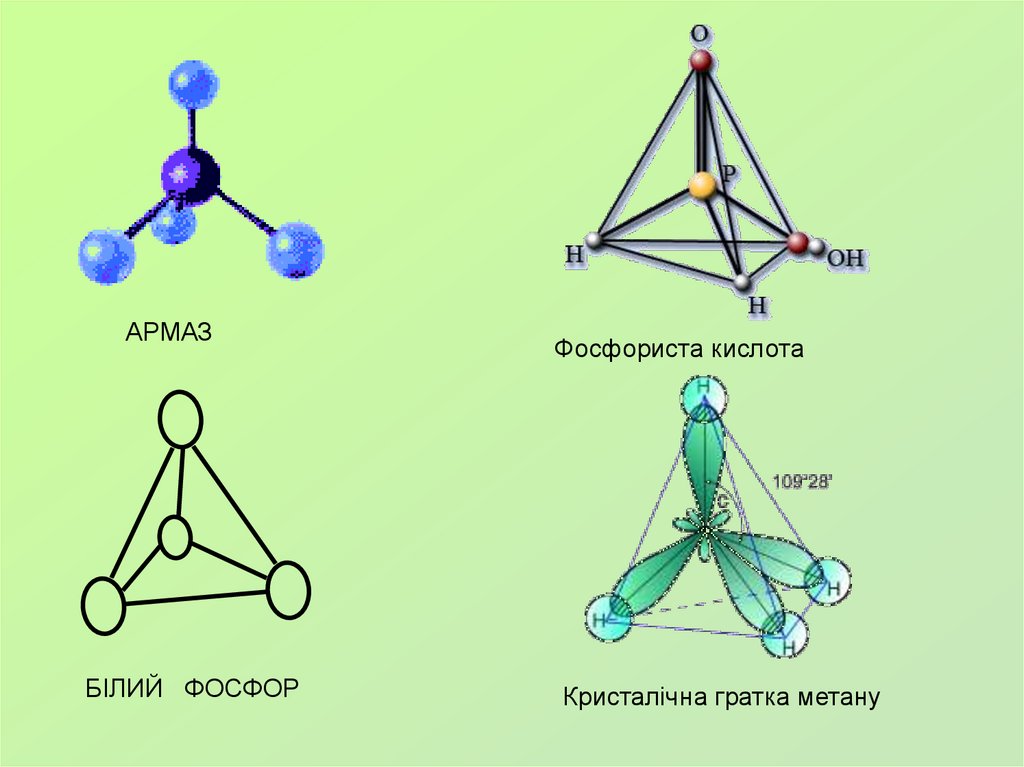
АРМАЗ
БІЛИЙ ФОСФОР
Фосфориста кислота
Кристалічна гратка метану

5.

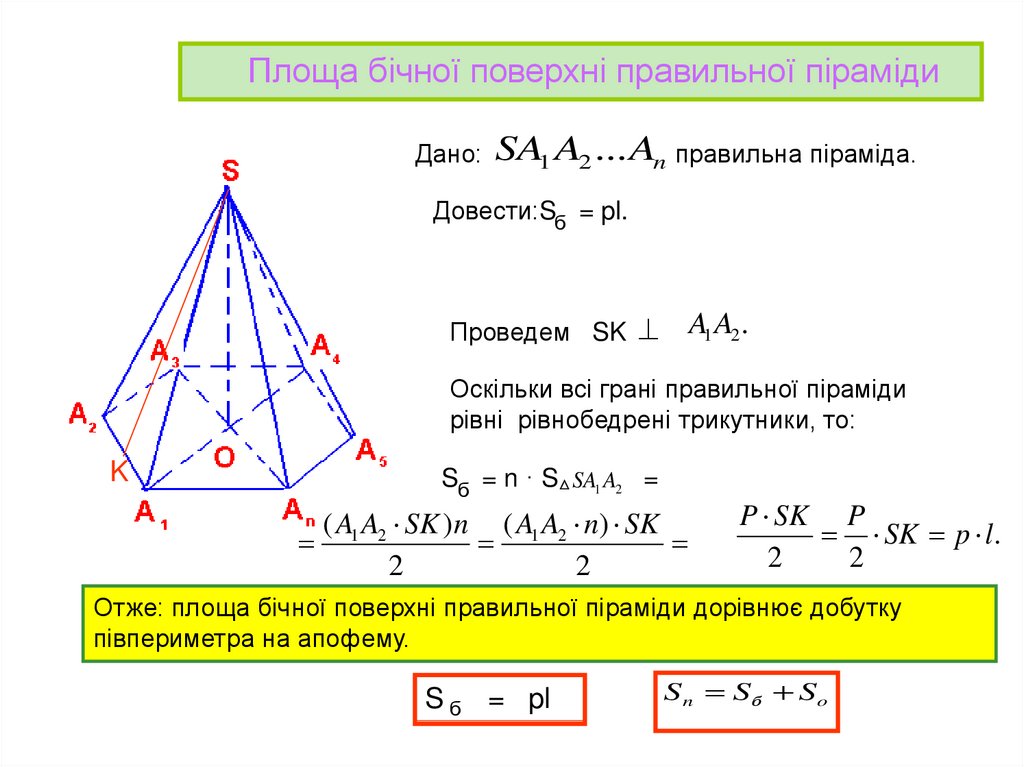
Площа бічної поверхні правильної піраміди
Дано: SA1 A2 ... An правильна піраміда.
Довести:Sб = pl.
Проведем SK
К
K
A1 A2 .
Оскільки всі грані правильної піраміди
рівні рівнобедрені трикутники, то:
Sб = n · S SA1 A2 =
( A A SK )n ( A1 A2 n) SK
1 2
2
2
P SK P
SK p l.
2
2
Отже: площа бічної поверхні правильної піраміди дорівнює добутку
півпериметра на апофему.
S б = pl
S n Sб So

6. Розв'яжіть усно

Дано:SABCD правильна піраміда
DC=3см
SK=4см.
Знайти: S б
К

7. Задача за готовим малюнком

Картка 7
Задача за готовим малюнком
Дано: SАВСD – правильна піраміда.
АВ =2см, SNA= 60°
Знайти: Sп
S
= So + Sб
п
S
ABC
Sб
a 2 3 22 3 4 3
3 (см 2 ).
4
4
4
1
= 2 3 АВ·SN.
AB 3 2 3
3
(см).
Оскільки ON радіус вписаного кола, то ON = 6
6
3
Оскільки кут OSN дорівнює 30°, то SN = 2ON = 2 3 (см).
3
1 3 2 2 3
Sб
2 3 (см 2 ).
Sn 3 2 3 3 3(см2 )
2
3
Відповідь: 3 3 (см 2 )

8.

Задача №2. Колективне розв’язання
ДАНО:SABС правильний тетраедр.
АВ = а. АМ = МВ
Знайти:
S MBC
MCB( M 90 )
MC
a 3
sin 60 , MC BC sin 60
.
BC
2
Точка О – центр описаного кола, тому ОС = R.
Як відомо
З
R
ВОС ( О 90 )
a 3 2
a2
2
SO SC OC a (
) a
3
3
2
2
2
a 3
a
МС SO
2
S MBC
2
2
a 3
.
3
2
2
3 a
2
4
.
маємо:
3a 2 a 2
3
2a 2
2
a .
3
3
Відповідь:
a2
2
4
.

9.

Домашнє завдання