Похожие презентации:
НСВ. Плотность распределения случайной величины
1. НСВ
2. Плотность распределения случайной величины
3.
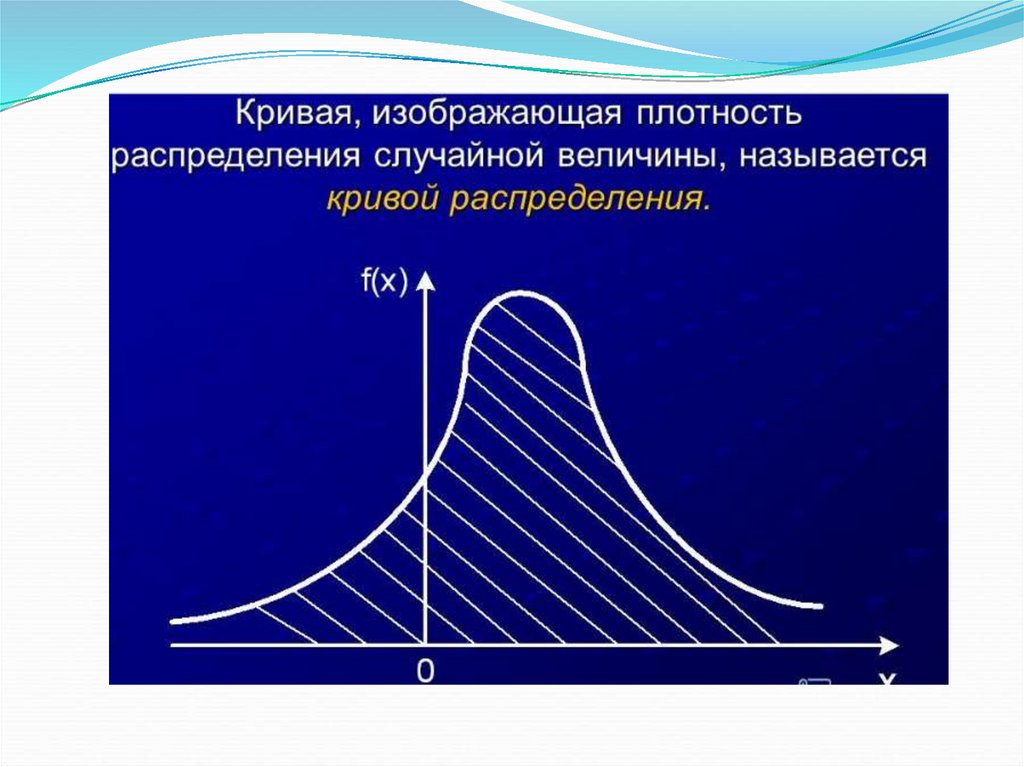
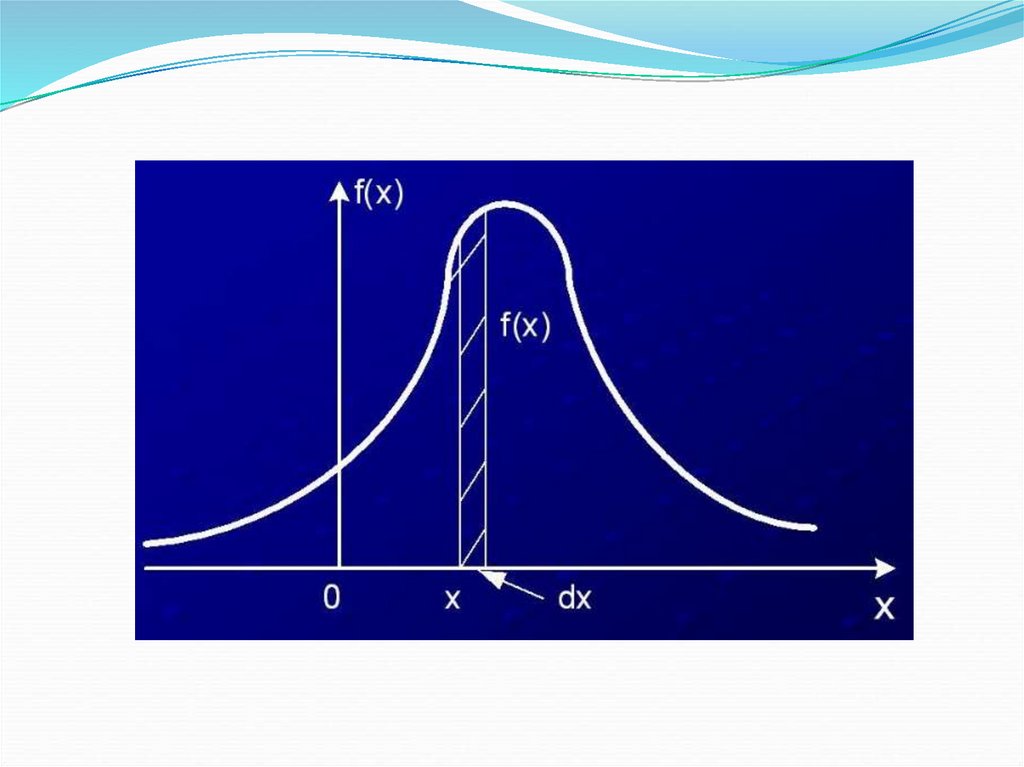
Плотностью распределениявероятностей непрерывной
случайной величины называют
производную ее функции
распределения.
4.
5.
6.
7.
8.
9.
Пример:10.
Пример:11.
Математическое ожидание НСВ12.
x 1;0,
f ( x) x 1, 1 x 2;
0,
x 2.
2
2
3
2
x
x
M ( X ) x ( x 1)dx ( x 2 x)dx ( )12
3 2
1
1
8
1 1
7 3 5
( 2) ( ) .
3
3 2
3 2 6
13.
Дисперсия непрерывной случайной величины• Дисперсией непрерывной
случайной величины называют
математическое ожидание
квадрата разности между этой
случайной величиной и ее
математическим ожиданием:
•Воспользовавшись формулой
для математического ожидания
непрерывной случайной
величины, возможные значения
которой принадлежат отрезку [a,
b]
14.
Случайная величина задана дифференциальнойфункцией распределения:
0, x 1;
f ( x) 3 x 2 , 1 x 0;
0, x 0
Найти M ( X ) и D( X ).
b
0
4
3
x
3
0
3
M ( X ) x f ( x)dx 3 x dx (
) 1 ;
4
4
a
1
0
0
3 2
3 2 2
2
D( X ) ( x ( )) 3 x dx 3 ( x ) x dx
4
4
1
1
0
5
4
3
3
9
x
3
x
9
x
0
4
3
2
3 ( x x x )dx 3( ) 1 0,0375
2
16
5 2 4 16 3
1
15.
Среднеквадратичное отклонение непрерывнойслучайной величины
Среднеквадратичное
отклонение для непрерывной
случайной
величины определяется так
же, как и для дискретной
случайной величины:








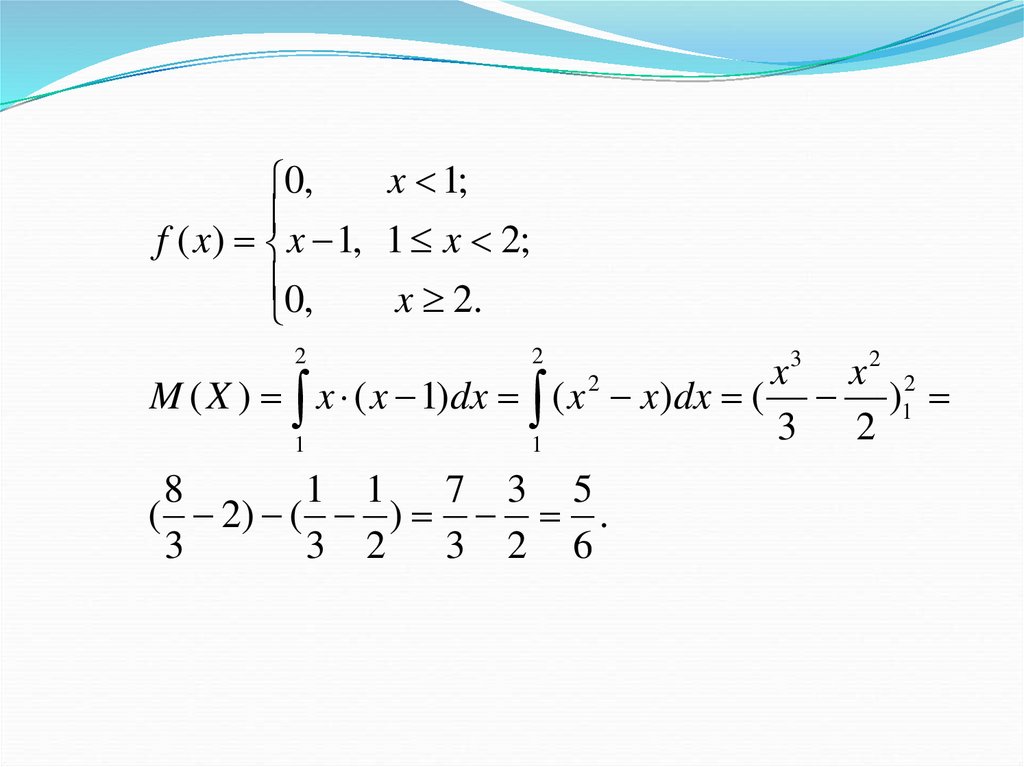




 Математика
Математика








