Похожие презентации:
Иррациональные неравенства
1.
Иррациональные неравенства2.
Иррациональными называютнеравенства, в которых
неизвестное Х находится под
знаком корня.
3.
4.
Алгоритм решения иррациональныхнеравенств:
1. Введение иррациональной функции;
нахождение области определения функции.
2. Вычисление нулей функции.
3. На координатной прямой:
• отмечаем нули функции, принадлежащие области
определения;
• определяем знак функции на каждом промежутке;
• с учетом знака неравенства выписываем ответ.
5.
Решим неравенства:1.
x 5 1
2.
x 7 x 1
3.
( x 1) x x 2 0
2
6.
x 5 1x 5 1 0
Шаг 1. Рассмотрим функцию
Найдем область определения:
Шаг 2. Вычислим нули функции
f ( x)
x 5 1
x 5 0
x 5
x 5 1 0
x 5 1
( x 5 ) 2 12
x 5 1
x 6
Шаг 3.
f (5.5) 5.5 5 1 0.5 1 0
f (7) 7 5 1 2 1 0
Ответ
x [5;6)
- нуль функции
7.
x 7 x 1x 7 x 1 0
Шаг 1. Рассмотрим функцию
Найдем область определения
Шаг 2. Вычислим нули функции
x 7 x 1
x 1 0
2
2
( x 7 ) ( x 1)
Шаг 3.
f ( x) x 7 x 1
x 7 0
x 7
x 7 x 1 0
x 1
x 1
x 1
2
2
x
x
6
0
x1 3; x 2 2
x 7 x 2x 1
f ( 6) 6 7 ( 6) 1 1 6 1 6 0
Ответ
x [ 7;2)
f (9) 9 7 9 1 4 10 6 0
8.
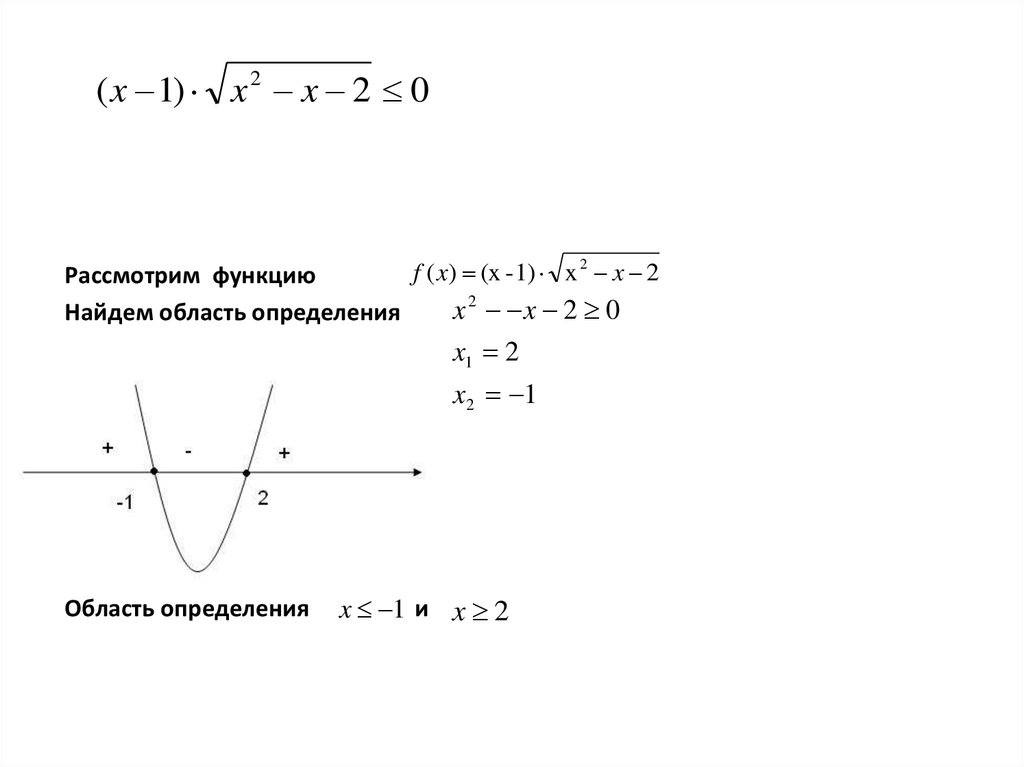
( x 1) x 2 x 2 0f ( x) (x - 1) x 2 x 2
Рассмотрим функцию
x2 x 2 0
Найдем область определения
x1 2
x 2 1
Область определения
x 1 и x 2
9.
( x 1) x 2 x 2 0Вычислим нули функции:
x 1 0
x1 1
x2 x 2 0
x2 x 2 0
x 2 1
f ( 3) 0
f (3) 0
x ( ;1]
( x 1) x 2 x 2 0
x 2
x3 2
10.
Домашнее задание1.
2x 9 3 x
2.
x 2 3x 10 8 x
3.
9 x 2 3 6x x 2







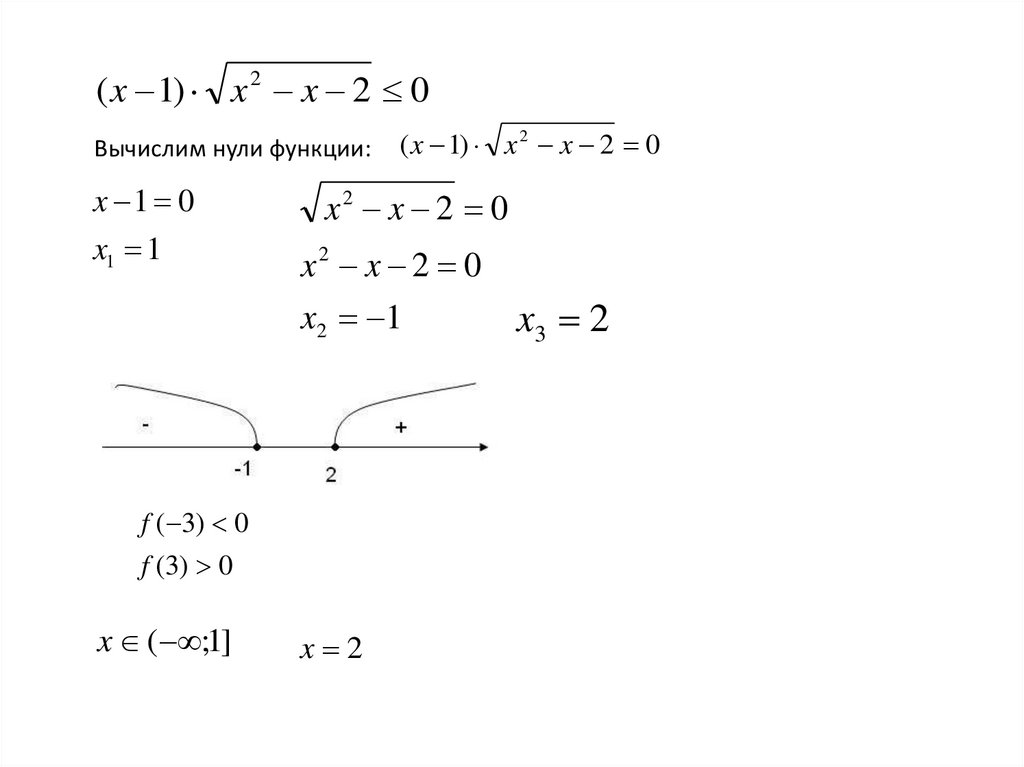

 Математика
Математика








