Похожие презентации:
Об'єм призми
1. Об'єм призми
2. Призма
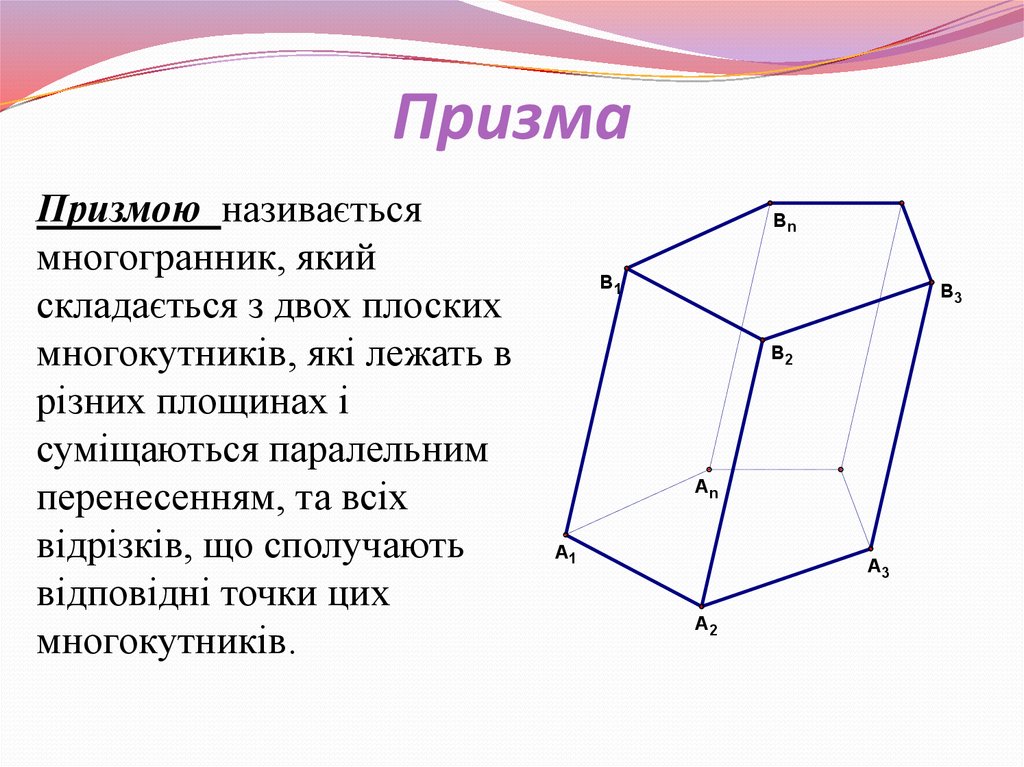
Призмою називаєтьсямногогранник, який
складається з двох плоских
многокутників, які лежать в
різних площинах і
суміщаються паралельним
перенесенням, та всіх
відрізків, що сполучають
відповідні точки цих
многокутників.
Bn
B1
B3
B2
An
A1
A3
A2
3.
BnB1
B3
Многокутники A1A2…An і
B1B2…Bn називаються
основами призми,
B2
An
Bn
A1
A3
B1
B3
A2
B2
а параллелограми –
бічнимими гранями
призми
An
A1
A3
A2
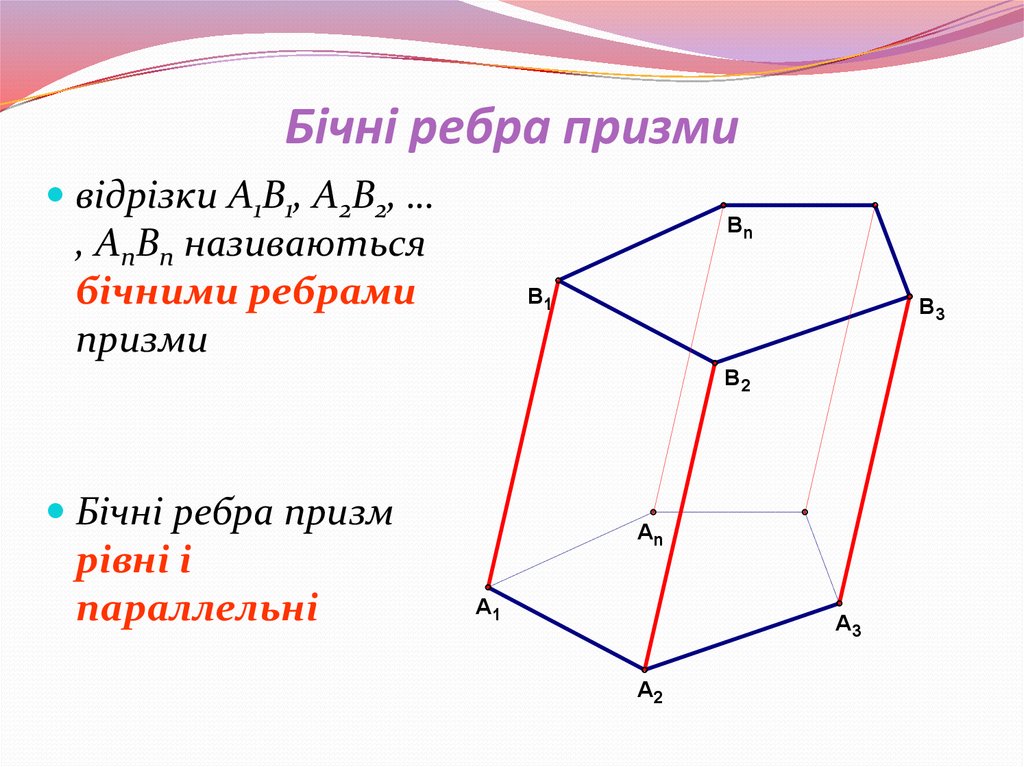
4. Бічні ребра призми
відрізки A1B1, A2B2, …, AnBn називаються
бічними ребрами
призми
Bn
B1
B3
B2
Бічні ребра призм
рівні і
параллельні
An
A1
A3
A2
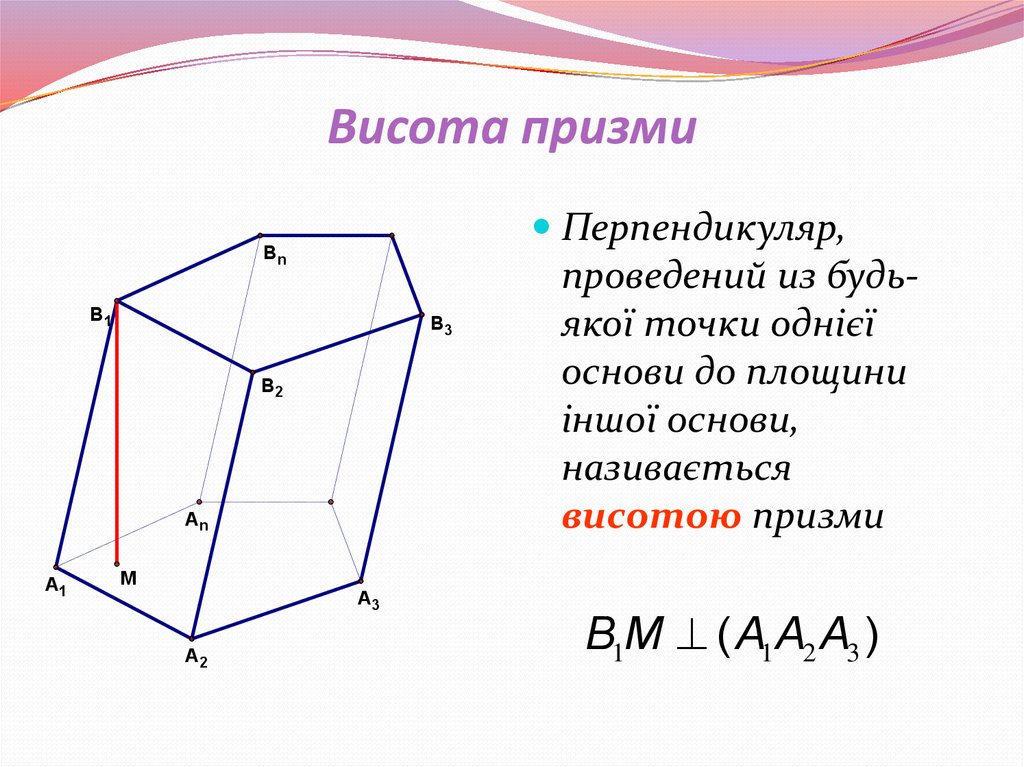
5. Висота призми
BnB1
B3
B2
An
A1
Перпендикуляр,
проведений из будьякої точки однієї
основи до площини
іншої основи,
називається
висотою призми
M
A3
A2
B1M ( A1A2 A3 )
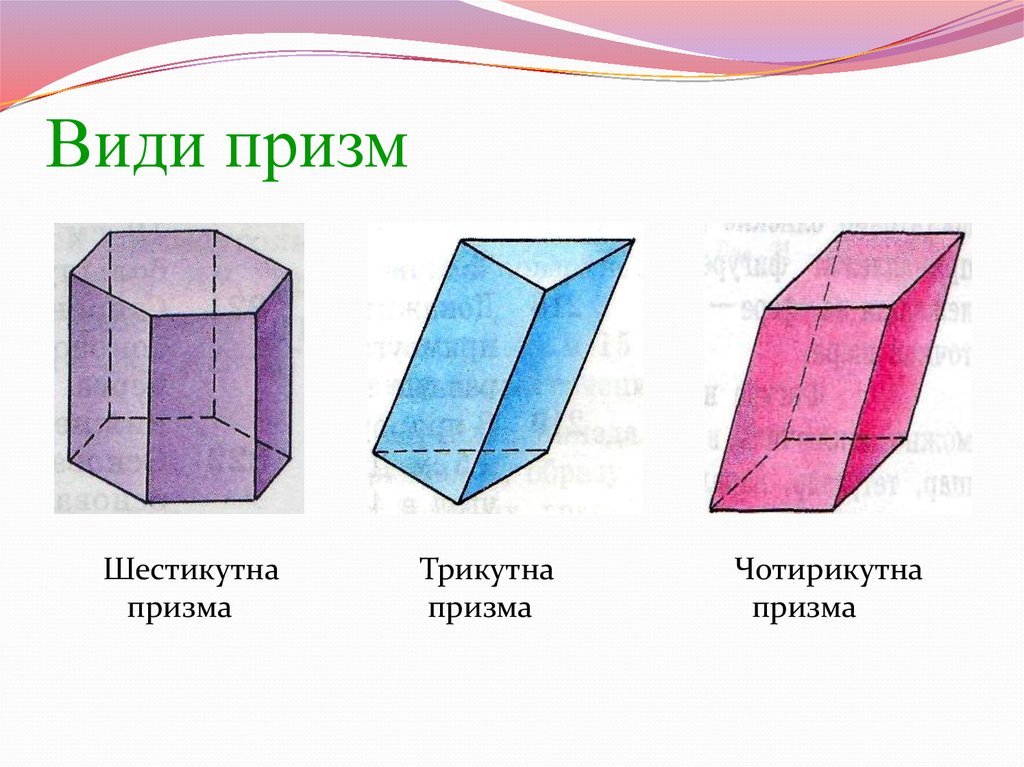
6. Види призм
Шестикутнапризма
Трикутна
призма
Чотирикутна
призма
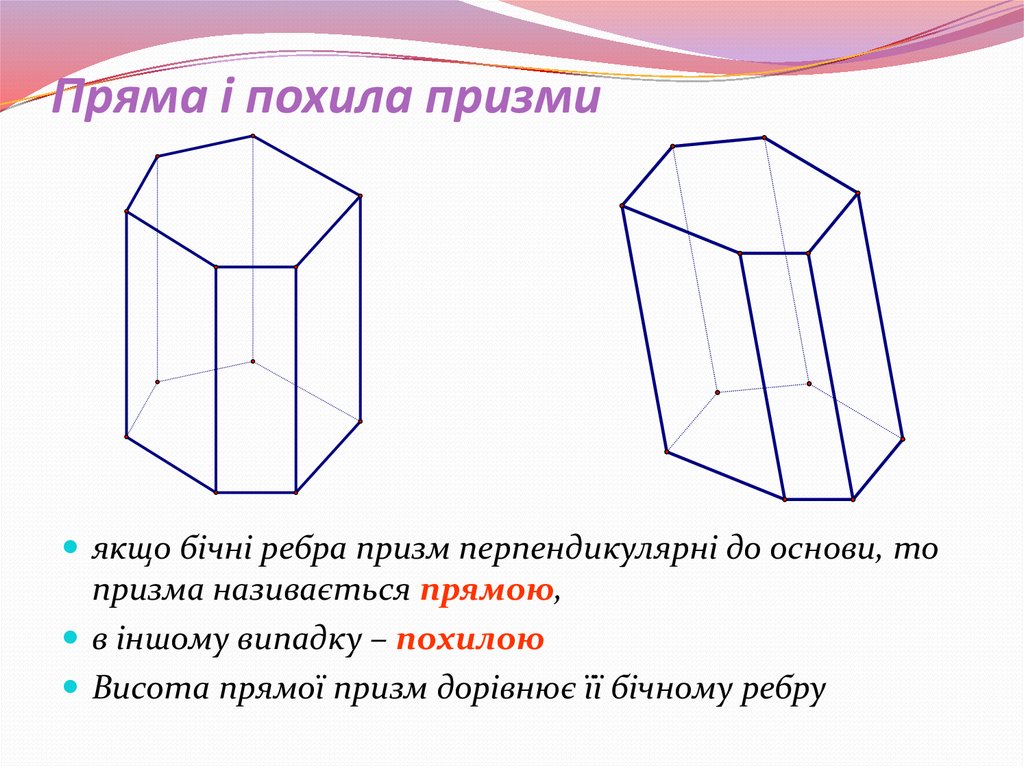
7. Пряма і похила призми
якщо бічні ребра призм перпендикулярні до основи, топризма називається прямою,
в іншому випадку – похилою
Висота прямої призм дорівнює її бічному ребру
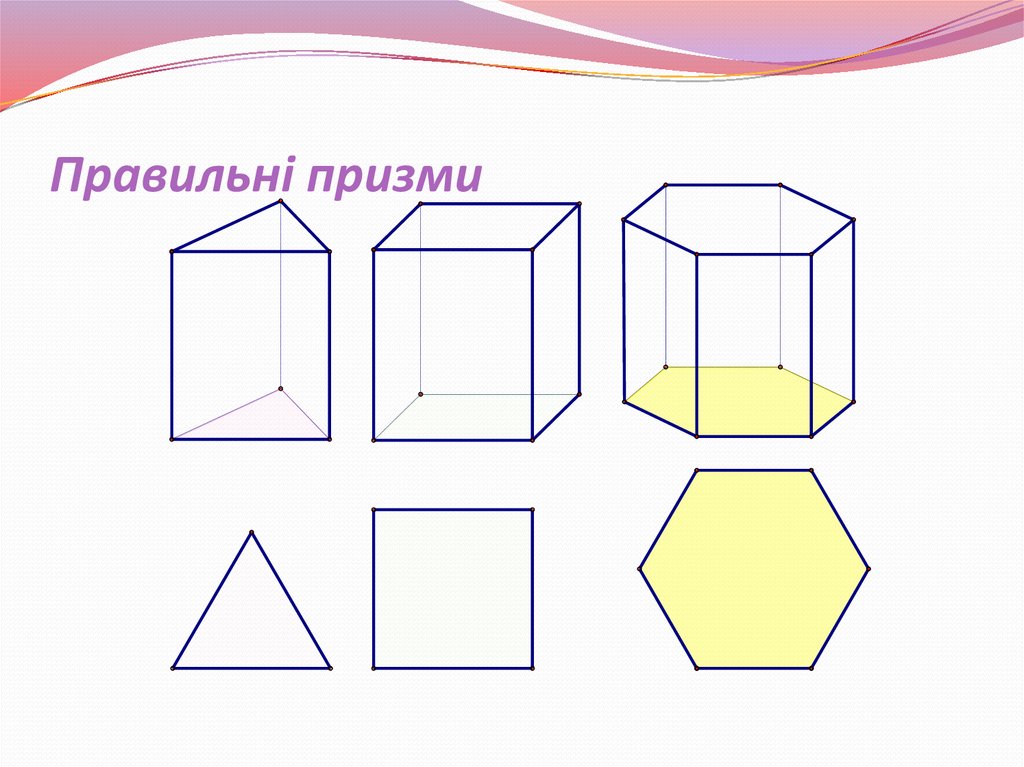
8. Правильна призма
Пряма призманазивається
правильною, якщо її
основи – правильні
многокутники
У правильної призми
всі бічні грані – рівні
прямокутники
9. Правильні призми
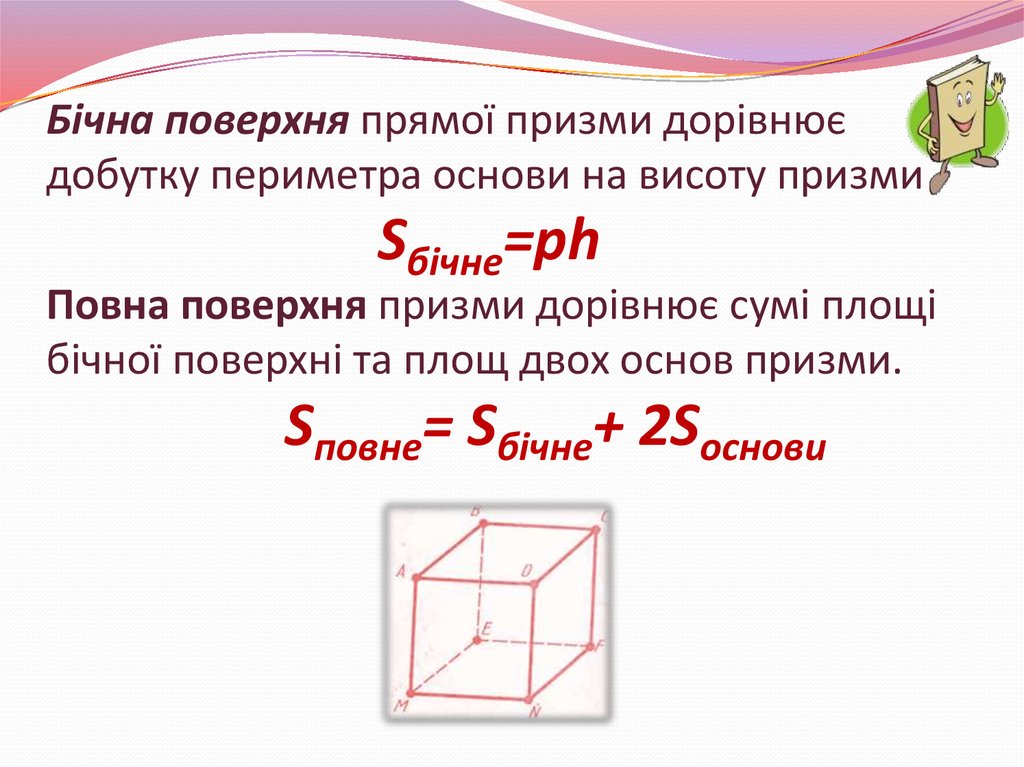
10. Бічна поверхня прямої призми дорівнює добутку периметра основи на висоту призми Sбічне=ph Повна поверхня призми дорівнює сумі площі бічної
Бічна поверхня прямої призми дорівнюєдобутку периметра основи на висоту призми
Sбічне=ph
Повна поверхня призми дорівнює сумі площі
бічної поверхні та площ двох основ призми.
Sповне= Sбічне+ 2Sоснови
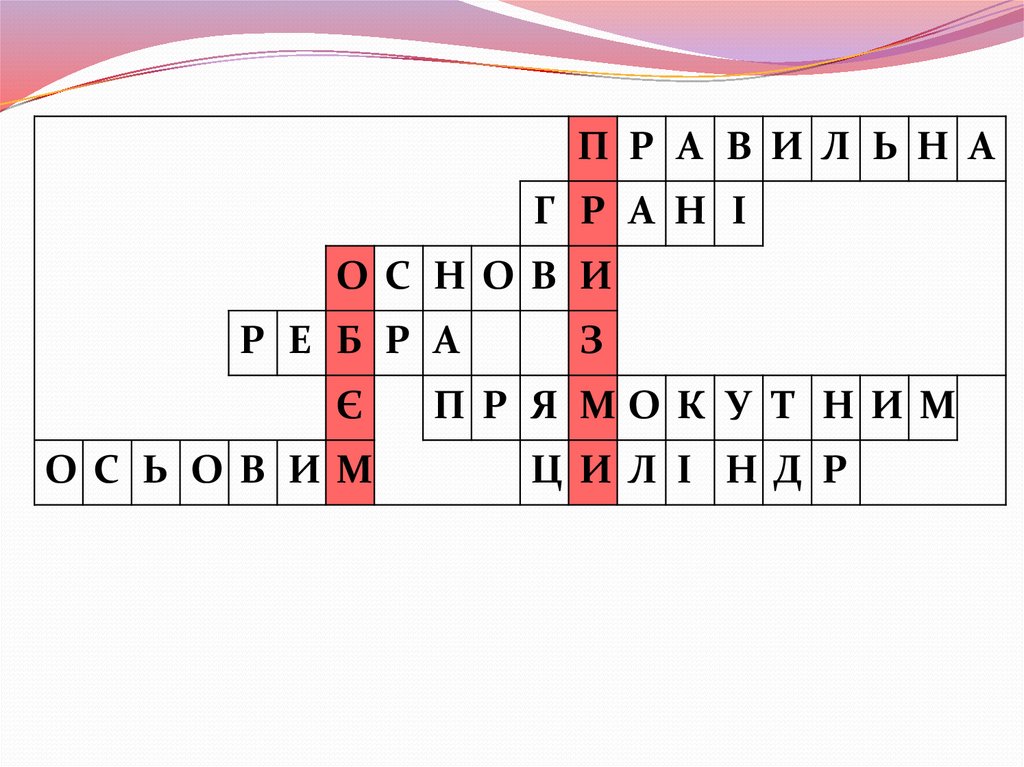
11.
П Р А В И Л Ь Н АГ Р А Н І
ОС НОВ И
Р Е Б Р А
Є
ОС Ь ОВ ИМ
З
П Р Я МО К У Т Н И М
Ц ИЛ І НД Р
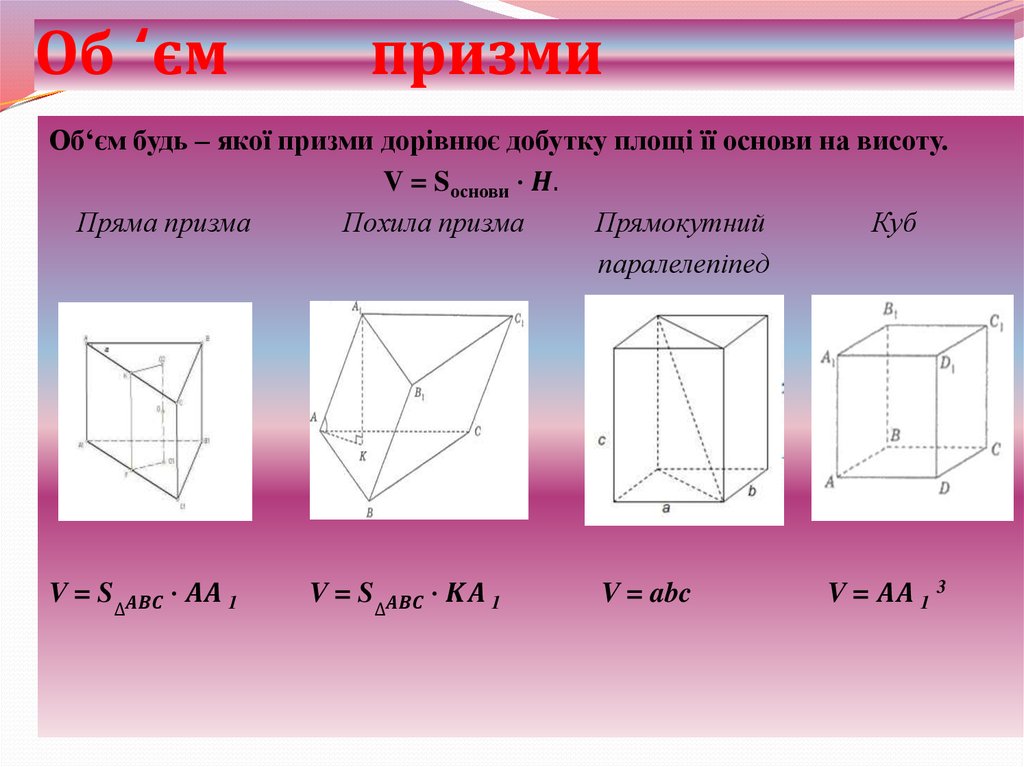
12. Об ‘єм призми
Об‘єм будь – якої призми дорівнює добутку площі її основи на висоту.V = Sоснови ∙









 Математика
Математика








