Похожие презентации:
Теория принятия решений
1.
Южный федеральный университетИнститут компьютерных технологий и информационной безопасности
Презентация к лекции №1
по дисциплине
«Теория принятия решений»
Лектор:
к.т.н., доцент каф. СиПУ
Кузьменко Андрей Александрович
andrew.kuzmenkosipu@gmail.com
aakuzmenko@sfedu.ru
2.
Цель и задачи дисциплиныЦель освоения дисциплины:
формирование базовых знаний о математических моделях, методах и алгоритмах
выбора эффективных решений при решении различных организационнотехнических задач с учётом факторов многокритериальности, случайности и
неопределенности; формирование умений применять полученные знания для
обоснования профессиональных решений.
Задачи:
сформировать знания и понимание основных понятий теории принятия
решений (ТПР), этапов процесса принятия решений, классификации задач и
методов, применяемых при формализации и оптимизации решений, методов
принятия инженерных решений в условиях определённости, неопределенности,
в условиях риска или конфликта, принципов принятия Парето-оптимальных и
коллективных решений;
сформировать умения построения формальных моделей прикладных задач
принятия решений; решать типовые задачи принятия решений и
оптимизировать их результаты; выбирать эффективные модели и методы для
решения инженерных задач; применять полученные знания для обоснования
профессиональных решений;
научить методам и моделям теории принятия решений; методам анализа
альтернатив при решении многокритериальных задач оптимизации; навыкам
решения задач рационального оценивания, выбора и принятия решений.
2
3.
Содержание лекционного материала дисциплины:Модуль 1. Предмет науки о принятии решений, однокритериальные методы
принятия оптимальных решений.
Предмет науки о принятии решений (ПР), процесс ПР. Постановка задач
принятия индивидуальных и групповых решений. Классификация задач и
методов ПР. Шкалы и методы измерения экспертных решений. Принятие
решений при полной информации: нелинейные распределительные
задачи, задачи упорядочения. Оптимальный выбор в условиях
противоборства: теория игр в задачах принятия решений. Теория
статистических решений. Дерево решений. Понятие о выборе в нечеткой
среде. Индивидуальные рациональные решения.
Модуль 2. Многокритериальные методы принятия решений. Коллективные
решения.
Задачи многокритериальной оптимизации. Определение важности
критериев. Свертка критериев. Парето-оптимальные решения.
Оптимальность по Слейтеру. Метод ELECTRE I. Метод анализа иерархий.
Метод главного критерия. Целевое программирование. Метод уcтупок.
Коллективный выбор. Принципы большинства, диктатора, Курно, Парето,
Эджворта. Процедуры голосования. Теорема Эрроу.
Автоматизация процесса поддержки принятия решений.
Контрольная работа №1.
3
4.
Учебная карта дисциплины№
Виды контрольных мероприятий
Текущий контроль
Рубежный контроль
1.
Работа на практических занятиях
15
-
2.
Индивидуальное задание
25
-
3.
Контрольная работа №1
-
10
4.
Контрольная работа №2
-
10
Всего
40
20
до 10 За академическую активность на лекционных и
баллов практических занятиях (до 5 баллов), досрочная сдача
индивидуального задания (до 5 баллов). Начисление
бонусных баллов производится на последнем занятии.
Письменный экзамен. Билет содержит:
Промежуточная
1. Теоретический вопрос 1 (12 баллов при полном
аттестация
ответе на вопрос).
в форме экзамена
40
баллов 2. Теоретический вопрос 2 (12 балов при полном
ответе на вопрос).
3. Задача (16 баллов).
Бонусные баллы
Объем дисциплины:
38 часов – лекционные занятия (6-15 неделя по 2 лекции в неделю);
38 часов – практические занятия (9-18) неделя по 2 занятия в неделю);
104 часа – СРС + экзамен.
Запись к лекторам общеинститутских дисциплин для 3-го курса в Личном
кабинете на сайте ИКТИБ до 28 марта.
4
5.
Электронное сопровождение дисциплиныlms.sfedu.ru система электронного обучения ИКТИБ
Особенности и преимущества использования:
o
электронные версии учебных материалов, в т.ч. презентации лекций
o
интерактивное взаимодействие с лектором, доска объявлений
o
электронная форма контрольной работы №1
5
6.
Рекомендуемая литература по дисциплине1. Родзин С.И. Теория принятия решений: лекции и практикум: учебное
пособие. – Таганрог: Изд-во ТТИ ЮФУ, 2010. – 336 с.
2. Петровский А.Б. Теория принятия решений: учебник для студ. вузов. – М.:
Академия, 2009. – 400 с.
3. Гладких Б.А. Методы оптимизации и исследование операций для
бакалавров информатики: учебное пособие. Ч. III. Теория решений.
– Томск: Изд-во НТЛ, 2012. – 281 с.
(http://www.csd.tsu.ru/sites/default/files/Хранилище/Предметы/Методы%20о
птимизации%20и%20исследование%20операций%201/OpRes-Part-3.pdf)
4. Таха Хемди А. Введение в исследование операций. – М.: Вильямс, 2007.
6
7.
Цель лекции №1:– обозначить предмет науки о ПР, основные понятия и определения, этапы
процесса ПР;
– сформулировать общую постановку задач принятия индивидуальных и
групповых решений;
– показать классификации задач и методов ПР.
Содержание лекции:
1. Предмет науки о ПР, процесс ПР.
2. Постановка задач принятия индивидуальных и групповых решений.
3. Классификация задач и методов ПР.
7
8.
1. Предмет науки о ПР, процесс ПРВ силу повторяемости, шаблонности ситуаций выбора человек принимает
решение, почти не задумываясь, часто интуитивно или по аналогии. В более
сложных и соответственно более редких, уникальных ситуациях, человек более
тщательно подходит к своему выбору старается детально рассмотреть, оценить и
сопоставить различные варианты, учесть разные точки зрения. Необходимость
обоснования выбора присутствует во всех сферах человеческой деятельности.
Необходимость принятия решения связана с наличием проблемной ситуации или
системной проблемы.
В ситуациях принятия сложных решений всегда существует недостаток
информации. Часть нужной информации нередко отсутствует, а имеющаяся
информация может быть противоречивой. Принятие верных решений в сложных
ситуациях является своего рода искусством, которым владеют немногие.
Возросла динамичность жизни; сократился период времени, в течение которого
принятые ранее решения остаются верными; повысилась сложность вариантов
принимаемых решений, их взаимозависимость и взаимосвязь; существенно
увеличились возможные риски и неопределённость последствий, масштабы и
размеры потерь в случае принятия недостаточно обоснованных решений. Как
следствие, существенно возросла ответственность человека за принятие
наилучшего, «самого правильного» решения, увеличились трудности, связанные с
его нахождением, преодолеть которые невозможно без использования всего
арсенала средств, накопленных современной теорией принятия решений.
9
9.
1010.
Понятие «решение» имеет смысловые значения:1) совокупность рассматриваемых возможностей, которые тем или иным
образом выделены человеком, делающим выбор (alternative, decision);
2) процесс поиска наиболее предпочтительных вариантов, включающий в себя
обдумывание, изучение какого-либо вопроса или задачи, нахождение
правильного ответа (solving, choice);
3) результат конкретного выбора варианта действий (solution, resolution);
4) указы, постановления, распоряжения, приказы, акты органов
законодательной и исполнительной власти, судебные и иные решения (degree,
order).
Принятие решений (decision making) – это вид человеческой деятельности,
который состоит в обоснованном выборе наилучшего, в некотором смысле,
одного или нескольких вариантов из имеющихся возможных и имеющий целью
достижение осознаваемого результата.
Задачи принятия решений часто отождествляются с задачами выбора,
являющимися одними из самых распространенных задач, с которыми
человек сталкивается в своей деятельности. При выборе решений главную
роль играет анализ их последствий.
11
11.
Изучением того, как человек принимает решения, и созданием методоввыбора занимаются многие научные дисциплины, которые возникли и
исторически развивались независимо друг от друга.
К ним относятся системный анализ, исследование операций, теория
статистических решений, теория игр, теория оптимального управления,
экономическая кибернетика, теория организаций, информатика,
искусственный интеллект, когнитивная психология, теория поведения и др.
Эти дисциплины с разных точек зрения анализируют механизмы, процессы
и правила выбора применительно к объектам различной природы и в
различных условиях их существования. Все вместе они образуют
многодисциплинарную науку, помогающую человеку сделать обоснованный
выбор.
Теория принятия решений (ТПР) – это прикладная междисциплинарная
наука, основанная на методах математики, статистики, экономики,
искусственного интеллекта, менеджмента, психологии. ТПР изучает
закономерности выбора людьми путей решения разного рода задач, а также
разрабатывает методы поиска наиболее выгодных из возможных решений.
ТПР как самостоятельное научное направление стала складываться в
середине XX в. в рамках методологии системного анализа, хотя самые
первые работы появились ещё в конце XVII в.
12
12.
Теория принятиярешений
Дескриптивная
(описательная)
Описывает реальное поведение и
мышление людей в процессе
принятия решений и называется
описательной или психологической
теорией решений.
Прескриптивная
(предписывающая)
Предписывает людям, как им
следует принимать эффективные
решения, и называется
нормативной теорией решений.
1. Как у людей возникает представление о ситуации принятия
решений?
2. Как люди оценивают последствия принимаемых решений?
3. Как люди оценивают вероятности различных факторов,
влияющих на принятие решений?
4. Какие правила и стратегии используют люди для принятия
решения в различных ситуациях?
5. Как на людей влияют различные факторы, управляющие
процессом принятия решений?
Методы, подходы,
технологии принятия
решений, разработка средств
поддержки и обоснования
принятия решения
13
13.
Формализованные методы принятия решения необходимы в следующихслучаях:
• существует некоторая проблема или проблемная ситуация, требующая
своего разрешения и имеющая неопределенности;
• альтернативы оцениваются по нескольким критериями, которые зачастую
противоречивы и требуют согласования с предпочтениями ЛПР;
• имеется несколько альтернатив, способов достижения цели, действий,
объектов, среди которых производится выбор. Если существует одна
возможность и выбор отсутствует, то нет и задачи принятия решения;
• присутствуют факторы, накладывающие определённые ограничения на
возможные ресурсы, пути решения проблемы, достижения цели. Эти
факторы определяются контекстом решаемой проблемы и могут иметь
различную природу: физическую, техническую, экономическую, социальную,
персональную и иную;
• имеется человек или группа лиц, которые заинтересованы в разрешении
проблемы, имеют полномочия для выбора того или иного варианта решения
и несут ответственность за выполнение принятого решения.
14
14.
Исследованиеопераций
Искусственный
интеллект
Методы
оптимизации
Экспертология
Психология
Теория
игр
Теория
вероятностей
ТПР
Эконометрика
Теория нечеткой
логики
Конфликтология
Основной объект ТПР это системная проблема (проблемная ситуация).
Предмет исследования ТПР – это закономерности выработки решений
для проблемной ситуации, закономерности моделирования проблемной
ситуации.
Назначение ТПР разработка научно обоснованных методов и
технологий подготовки и принятия решений в сложных системах, а также
разработка средств автоматизации поддержки и обоснования решения
систем поддержки принятия решений, помогающих человеку в задачах
выбора.
15
15.
Становление теории принятия решенияПроблемы ПР обозначены в древнейших культурологических источниках –
эпосах, сказках и др. Среди её первых основателей числятся Платон и
Аристотель, считавшие, что способность принимать решения отличает людей
от животных.
Но наиболее значимыми фигурами среди основателей теории принятия
решений считаются И. Лойола (XV-XVI в.) и особенно Б. Франклин (XVIII в.),
который прекрасно владел методом попарных сравнений альтернатив и выбора
из них наилучшей.
Проблема голосований при различного рода выборах обсуждалась ещё
философами Древнего Рима, а формализованное представление она получила
в работах Ж.-К. де Борда и Ж. Кондорсе (XVIII в.).
Существенную роль в становлении теории принятия решений сыграли
И. Бентам (XVIII в.), предложивший подсчитывать сумму полезностей, и
У. Эджворт и В. Парето (XIX в.), развившие аппарат кривых безразличия.
Становлению теории принятия решений во многом содействовали в качестве
изобретателей теории игр Е. Борель и Дж. фон Нейман (ХХ в.).
В 1960-1970-х гг. усилиями Т. Купмэнса, X. Куна, А. Такера, А. Чарнса,
У. Купера и Б. Ройя теории принятия решений был придан её современный вид.
Начиная с 1970-х гг. в развитии многокритериального анализа решений
наступил настоящий бум.
16
16.
Хугин и Мунин — пара воронов в скандинавской мифологии, которые летают повсему миру Мидгарду и сообщают богу Одину о происходящем. На древнеисландском
Huginn означает «мыслящий», а Muninn — «помнящий» (или «мысль» и «память»
соответственно).
17
17.
Жизнь – это совокупность принятых решений.NN.
18
18.
Паскаль (1670) предложил процедуру вычисленияожидаемой ценности решения при выборе в условиях
неопределённости из нескольких вариантов. Эту идею он
использовал в известном пари о вере в Бога. Личная вера
или неверие в Бога — выбор каждого, однако даже если
вероятность существования Бога невелика, согласно
Паскалю, ожидаемая ценность веры превышает ценность
неверия.
Бернулли (1738) опубликовал Санкт-Петербургский
парадокс: голландский торговец решает, застраховать ли
груз, посылаемый из Амстердама в Петербург зимой, при
условии, что есть 5 %-ный шанс потери судна и груза.
Лагранж (1801) решил задачу, смысл которой заключался
в следующем: сколько земли должен брать землекоп на
лопату, чтобы его производительность за смену была
максимальной. Утверждение «бери больше, кидай
дальше» оказалось неверным.
19
19.
Лицо, принимающее решение (ЛПР) – это индивид, который реально осуществляет выборнаилучшего варианта действий и несет ответственность за принятые решения в
соответствии со своими полномочиями.
Владелец проблемы (ВП) – это индивид, имеющий основания и мотивы для постановки
проблемы, осознающий необходимость ее решения, инициирующий тем или иным образом
принятие и выполнение нужного решения. В общем случае ЛПР и ВП – не одно лицо.
В качестве отдельных лиц, принимающих решения, выступают руководители и члены
выборных органов, жюри, комитетов, судьи, эксперты, избиратели и т. п. Совокупность
таких действующих лиц называют группой, принимающей решение (ГПР) независимо от
роли и значимости каждого члена группы в процессе решения задачи выбора.
Аппарат ЛПР – группа людей, осуществляющая подготовительные мероприятия для
принятия решения.
Активная группа – группа людей, объединенная общим интересом и старающаяся оказать
влияние на процесс принятия решения и его результат.
Эксперты – люди, которые профессионально лучше, чем ЛПР, знают отдельные аспекты
проблемы и выступают в роли источника информации, необходимой для принятия решения.
В подготовке сложных решений, имеющих обычно стратегический характер, принимают
участие системные аналитики. Их роль заключается в рациональной организации процесса
принятия решений. Аналитик, в отличие от эксперта, обычно не дает никаких личных
оценок, а только помогает ЛПР уяснить свои предпочтения, взвесить все «за» и «против» и
прийти к компромиссному решению.
20
20.
Ограничения – соотношения в виде равенств и/или неравенств, задающихдопустимую область существования решения задачи.
Область допустимых решений (допустимое множество) D – область
в n-мерном пространстве переменных состояния (параметров) задачи, которая
содержит решения, удовлетворяющие всем ограничениям задачи.
В процессе принятия решения формируются альтернативы, а также
оценивается их предпочтительность. Для этого:
индивидуальное ЛПР определяет критерий выбора;
групповое ЛПР вырабатывает принцип согласования группового
выбора.
Альтернатива – вариант решения:
X i xij , j 1, n , X i D
Целевая (критериальная) функция (критерий оптимальности, эффективности и
др.) – некоторая характеристика, позволяющая
оценить полезность альтернатив, сравнить их между собой. Она устанавливает
принцип оптимальности, отражающий предпочтения ЛПР.
Xi
X j F Xi
F X j , X k D
21
21.
Оптимальное решение – решение, которое в некотором смыслепредпочтительнее всех решений из области допустимых решений.
Также справедливо, что это допустимое решение, которое доставляет
оптимум (минимум или максимум ) целевой функции.
F X i , X i D
X* D F X*
Отметим, что методы многокритериальной оптимизации как правило
НЕ ДАЮТ оптимального решения, поскольку невозможно получить решение,
обеспечивающее наилучшее (максимальное/минимальное) допустимое
решение по всем критериям одновременно.
Получаемое решение будет компромиссным, учитывающим важности
критериев. Такие решения еще называют эффективными.
22
22.
Структуризация проблемной ситуацииПроблема (необходимость) принятия решения связана с наличием
проблемной ситуации или системных проблем. Точно определить это
понятие в виде какой-либо исчерпывающей формулировки невозможно.
Вместе с тем, обобщая опыт научных исследований, можно выделить
девять признаков, предложенных американским ученым в области ПР
Гербертом Саймоном и позволяющих в совокупности идентифицировать
системные проблемы:
Признаки системных проблем
23
23.
1. Слабо структурированные проблемы, содержащие как качественные, таки количественные элементы, причем качественные,
малоизвестные, неопределенные стороны имеют тенденцию доминировать.
Именно этими проблемами занимается системный анализ.
Им противопоставлены:
- хорошо структурированные или количественно сформулированные проблемы,
в которых существенные зависимости выяснены настолько хорошо и полно, что
они могут быть выражены в числах или символах, получающих в конце концов
количественные оценки. Эти проблемы составляют предмет теории
оптимизации, исследования операций, теории управления;
- неструктурированные, или качественно выраженные проблемы, содержащие
лишь словесные описания важнейших аспектов изучаемого объекта, его
признаков и характеристик, количественные зависимости между которыми
неизвестны. Эти проблемы входят в круг интересов гуманитарных наук –
социологии, психологии, экономики, политологии, юриспруденции и др.
Основные методы решения данных проблем – это экспертные методы,
имитационное моделирование.
2. Конфликтность. Системные проблемы формируются противоречиями
между частями системы, ее внешним окружением, субъектами принятия
решения, критериями оценки и всегда ограниченными возможностями
практической реализации, например, ресурсами.
24
24.
3. Неопределенность. Содержательную сторону системных проблем можноописать лишь возможными сценариями (вариантами) развития событий, в
которых нет исчерпывающих данных относительно модели задачи
(ограничений, целевых функций), условий, сопровождающих данную
задачу, ее связей с другими проблемами и ресурсов, потребных для ее
разрешения, предпочтений ЛПР. Как показывает практика, проявленная
часть системной проблемы несет в себе не более 5-10% от общего объема
информации, необходимой для ее разрешения, а остальная часть скрыта от
исследователя и начинает появляться только в процессе caмoгo
исследования. Для системных проблем характерен широкий диапазон
неочевидных способов и приемов их разрешения, но полный набор
возможных вариантов не может быть определен заранее. Разрешение
системной проблемы часто связано с пересмотром устоявшихся взглядов на
природу вещей, с поиском принципиально новых альтернатив (стратегий).
Неопределённые факторы можно разбить на три группы.
1) неопределённость природы, т.е. факторы людям попросту неизвестные
или от них не зависящие;
2) неопределённость человека, который может вести себя
непоследовательно, противоречиво, допускать ошибки, зависеть от других
лиц (партнёров, противников и т.д.), чьи действия он не может полностью
учесть или предвидеть;
3) неопределённость целей, которые могут различаться и не совпадать друг
с другом.
25
25.
4. Неоднозначность. Системная проблема имеет несколько вариантов своегоразрешения, которые затруднительно ранжировать по их
предпочтительности. Интуиция (подкреплённая знаниями) и научное
творчество играют при принятии решений существенную, а порой
решающую роль, выступая источником зарождения новых идей и способов
разрешения системных противоречий.
5. Наличие риска. Для разрешения любой системной проблемы требуются
определенные ресурсы (финансовые, материальные, информационные и др.),
вложение которых непременно сопровождается элементами риска,
обусловленными противодействием со стороны как внешних, так и
внутренних сил. Природа противодействия объективна и связана с тем, что
любой вариант разрешения системной проблемы отвечает интересам одних
субъектов и ущемляет интересы других. Взаимосвязь интересов возникает в
результате корреляции данной проблемы с другими проблемами из-за
общности используемых ресурсов, потребных для их совместного
разрешения.
Никакие дополнительные ресурсные вложения не могут гарантировать
бесконфликтного разрешения данной системной проблемы (дополнительные
ресурсы порождают новые проблемы), а любой вариант ее разрешения не
является наилучшим, так как неизвестно, каким образом разрешаются
другие связанные с ней проблемы.
26
26.
6. Многоаспектность. Системные проблемы затрагивают множестворазнородных сторон той системы, в которой они возникают и развиваются,
а между этими сторонами существуют связи взаимного влияния.
Разрешение технических проблем всегда связано с вопросами
экономического, финансового, производственного, технологического,
экологического и др. характера.
Попытки упростить проблему путем исключения так называемых
«несущественных» аспектов приводят к ошибкам, которые жестоко мстят
за себя. В то же время стремление к полному учету всех сторон приводит к
тому, что проблема становится необозримой и практически неразрешимой.
7. Комплексность. Системные проблемы затрагивают аспекты многих
научных дисциплин (математики, физики, психологии, биологии,
кибернетики, социологии и др.), но ни одна из них в отдельности не
способна предложить эффективные способы их целостного разрешения.
Эффективно разрешить системную проблему можно только в том случае,
если привлечь адекватный по сложности комплекс научных методов и
знаний, охватывающий своими познавательными возможностями все
многообразие сторон и проявлений исследуемого объекта.
27
27.
8. Саморазрешимость. Это необычное свойство системных проблемзаключается в их способности разрешаться естественным образом, то есть
без приложения научных методов и знаний.
Вопрос заключается в том, какими могут быть последствия такого
саморазрешения: негативными или позитивными, конструктивными или
деструктивными. И задача ЛПР состоит в изыскании конструктивных
способов и технологий разрешения возникающих проблем, исключающих
негативные варианты развития событий в данной проблемной области.
9. Эволюционность. Любая системная проблема есть продолжение какойлибо проблемы прошлого, и сама является источником новой проблемы.
Цикл, в котором одна проблема переходит в дpyгую, не только никогда не
прерывается, но имеет тенденцию к разветвлению (одна проблема
порождает множество других). Отсюда возникает задача поиска таких
вариантов разрешения проблемы, которые: исключают возникновение
новых, еще более трудноразрешимых проблем; не содержат в себе
потенциала разрушения того позитивного, что было уже ранее создано
природой или обществом; не нарушают, а поддерживают преемственность
в развитии научных направлений так, чтобы каждое новое исследование не
начиналось заново.
28
28.
ТПР выделяет в процессепринятия решения
следующие этапы:
Примеры типовых ошибок,
допускаемых в процессе
принятия решений:
ОТКЛАДЫВАНИЕ
РЕШЕНИЯ
ПОЛНОСТЬЮ
ПОЛАГАТЬСЯ НА
ИНТУИЦИЮ
ПРИНЯТИЕ
ПОСПЕШНОГО РЕШЕНИЯ
НЕ ОТДЕЛЯТЬ ГЛАВНОЕ
ОТ ВТОРОСТЕПЕННОГО
ЧРЕЗМЕРНЫЕ ЗАТРАТЫ
НА РЕШЕНИЕ
ЗАНИМАЕТСЯ ТОЛЬКО
ЛЕГКИМИ
ПРОБЛЕМАМИ
29
29.
Классификация видов решенийПризнаки
Содержание решаемых задач
Уровень принятия решения
Количество целей
Субъект, принимающий решение
Время действия
Цикличность
Степень формализации и
программируемости
Виды решений
Научно-технические, технологические,
экономические,
политические,
социальные, правовые и др.
Государство, регион, организация,
малая группа, личность
Одноцелевые, многоцелевые
Индивидуальное ЛПР, групповое ЛПР
Стратегические, тактические,
оперативные
Разовые, повторяющиеся
Запрограммированные (на основе
стандартных процедур и правил);
незапрограммированные (требующие
новых процедур или правил принятия
решений)
30
30.
Способ обоснованияСтепень сложности, соответствие
ограничениям и цели
Условия принятия решений
Размерность решения
Требования к виду решения
Интуитивные
(основанные
на
чувствах и ощущениях человека),
логические (основанные на знаниях,
опыте и логических рассуждениях),
рациональные
(основанные
на
объективном анализе проблемных
ситуаций с использованием научных
методов и компьютерных технологий)*
Простые, сложные, уникальные,
допустимые, удовлетворительные,
оптимальные, эффективные
(компромиссные)
Принимаемые
в
условиях
определённости, риска (вероятностной
определённости),
неопределённости
(природы, человека, целей)
Один или много критериев принятия
решений,
количество
вариантов
решений
Один наилучший вариант, разделение
вариантов
решений
на
классы,
упорядоченные по качеству варианты
31
31.
2. Постановка задач принятия индивидуальных игрупповых решений
В ТПР выработка решения в основном направлена на определение
наилучшего (оптимального или компромиссного) способа (варианта)
действий для достижения поставленной цели.
Под целью понимается идеальное представление желаемого состояния или
результата деятельности.
Если фактическое состояние не соответствует желаемому, то имеет место
проблема. Выработка плана действий по устранению проблемы – одна из
центральных задач ТПР.
Возникновение проблемы связано с определёнными условиями. Эти условия
в ТПР называют ситуациями. Совокупность проблем и ситуаций образуют
проблемную ситуацию.
32
32.
Для индивидуального ЛПР общая постановка задачи принятия решениязаписывается в виде:
ИЛПР S 0 , T , Q | S , A, B, Y , F , K , Y *
Cлева от вертикальной черты находятся исходные данные задачи
принятия решения, справа – неизвестные:
S0 проблемная ситуация,
T время
для принятия
решения, Q ресурсы;
Вербальная
формулировка
задачи
S
множество
альтернативных
ситуаций ЛПР:
(внешней
среды),
принятия
решений индивидуальным
доопределяющих исходную проблемную ситуацию до полной группы
или гипотетических
ситуаций,
причёмQ,
ввзаимоисключающих,
условиях проблемнойнезависимых
ситуации S0, располагаемого
времени
T и ресурсов
сумма вероятностей
их возникновения
равна 1; альтернативных ситуаций S
необходимо
доопределить
ситуацию множеством
A – множество
(внешней
среды),целей,
сформулировать множество целей A, ограничений B,
B – множество ограничений
при принятии
решений;
альтернативных
решений Y, произвести
оценку
предпочтений функции F и найти
Y множество
альтернативных
вариантов
решений, Y,изруководствуясь
которых должно
оптимальное
(эффективное)
решение
Y* из множества
быть
выбраноK. (возможно
единственное)
оптимальное
(или
критерием(ями)
компромиссное) решение Y*;
F = F(A, S, Y) – функция предпочтения для оценки решений;
K – критерий(и) выбора решения Y*.
33
33.
Схема процесса принятия решений34
34.
Для группового ЛПР (ГЛПР) общая постановка задачи принятия решенияимеет вид
ГЛПР S 0 , T , Q | S , A, B, Y , F , L, Y * ,
где
F = F(F1,F2,…,Fk) – функция группового предпочтения, зависящая от
индивидуальных предпочтений лиц, входящих в ГЛПР;
L – принцип согласования индивидуальных предпочтений (например,
принцип большинства).
Вербальная формулировка задачи
принятия решений групповым ЛПР:
в условиях проблемной ситуации S0, располагаемого времени T и
ресурсов Q, необходимо доопределить ситуацию множеством
альтернативных ситуаций S, сформулировать множество целей A,
ограничений B, альтернативных решений Y, произвести оценку функции
группового предпочтения F и найти оптимальное решение Y* из
множества Y, руководствуясь принципом согласования L.
35
35.
Математическая модель принятия решений содержит [3]:1) множество варьируемых параметров, переменных состояния;
2) множество ограничений, формирующих область допустимых решений
задачи;
3) множество критериев оптимальности (целевых функций, критериев
оптимальности, эффективности);
4) метод выбора наилучшего решения из множества допустимых.
X - управляемые факторы (переменные, параметры состояния системы)
- неуправляемые факторы
Y - выходные факторы, определяющие исход (результат)
F (Y) - вектор целевых (критериальных) функций
uij - оценка (полезность) i-го исхода Y по j-му критерию, которая может быть
получена как в результате объективных измерений (прибыль, расход, затраты,
энергоемкость, надежность), так и иметь субъективный характер (красота,
удобство и т.п.)
36
36.
Постановка задач принятия решений для индивидуального и группового ЛПРпозволяет сформулировать ряд утверждений, которые характеризуют
большинство технических, управленческих и организационных решений:
1. Количество неизвестных элементов задачи принятия решений может
быть существенно больше, чем известных.
2. Эксперты, привлекаемые ЛПР для принятия решений, выполняют
вспомогательную роль, однако в реальности в некотором роде также
несут ответственность за свои рекомендации.
3. Оценка решения должна производиться на основе сравнения
альтернативных вариантов решений.
4. В условиях неопределённости может не существовать единственного
оптимального решения.
5. Для ЛПР с различными предпочтениями оптимальные решения могут
оказаться различными.
37
37.
3. Классификация задач и методов ПР1. По степени формализации:
Сложность задачи принятия решений во многом определяется степенью
формализации модели проблемной ситуации. Поэтому задачи принятия
решений принято разделять на три группы:
1) хорошо структурированные задачи;
2) слабоструктурированные;
3) неструктурированные задачи.
38
38.
2. По степени определённости информации:1) Общую задачу принятия решения, если в постановке задачи
неопределёнными (неизвестными) являются множество альтернативных
вариантов решений Y, критерий выбора наилучшего решения K или
принцип согласования предпочтений L.
2) Задачу выбора решения, если известно множество Y, а критерий
выбора К или принцип согласования L являются неопределёнными.
3) Задачу оптимизации, если Y, K или L известны и определены.
3. По числу ЛПР:
1) задачи принятия решения индивидуальным ЛПР;
2) задачи принятия решения групповым ЛПР.
4. По количеству целей и критериев ПР:
1) одноцелевые и многоцелевые задачи;
2) однокритериальные и многокритериальные задачи.
39
39.
5. По виду неконтролируемых факторов:1) задачи принятия решений в условиях определенности (отсутствуют
неконтролируемые факторы);
2) задачи принятия решений в условиях неопределенности (присутствуют
неконтролируемые факторы):
а) принятие решение при риске - случайные неконтролируемые
факторы – в конкретной ситуации не известны, но могут быть известны
статистические характеристики по прошлому опыту;
б) принятие решений при незнании (игры против природы) –
рассматривается теория статистических решений;
в) принятие решений при противодействии (теория игр).
6. По мощности множества альтернатив:
1) задачи условного выбора - допустимое множество альтернатив задается
неявно, с помощью системы равенств или неравенств – ограничений,
соответственно множество содержит бесконечное множество альтернатив;
2) задачи выбора на конечном множестве альтернатив - допустимое
множество альтернатив жестко задано. Как один из возможных вариантов –
это когда имеется начальное множество альтернатив, которое в процессе
обсуждения расширяется, т.н. конструируемое множество.
40
40.
7. По виду конечного решения:1) задачи классификации - множество альтернатив необходимо разбить
на группы или классы по определенному признаку, а потом эти классы
упорядочиваются по степени важности для ЛПР;
2) задачи ранжирования - альтернативы разбиваются на классы, но
внутри класса альтернативы упорядочиваются по степени важности;
3) задачи выбора наилучшей альтернативы - выбирается наилучшая
альтернатива по требуемому критерию эффективности (векторному
или скалярному).
8. По содержанию решения:
- технические задачи;
- экономические задачи;
- политические задачи и т.п.
9. По времени и значимости:
- долговременные задачи;
- среднесрочные задачи;
- краткосрочные задачи;
- тактические задачи;
- стратегические задачи.
41
41.
Южный федеральный университетИнститут компьютерных технологий и информационной безопасности
Презентация к лекции №2
по дисциплине
«Теория принятия решений»
Лектор:
к.т.н., доцент каф. СиПУ
Кузьменко А.А.
andrew.kuzmenkosipu@gmail.com
42.
Цель лекции:– обозначить основные понятия о измерениях в ТПР;
– охарактеризовать шкалы измерений в ТПР;
– представить методы субъективных измерений в ТПР.
Содержание лекции:
1. Шкалы измерений в ТПР.
2. Методы субъективных измерений в ТПР.
43
43.
1. Шкалы измерений в ТПРЛПР (или эксперт) в ходе принятия решений формирует проблемную
ситуацию, цели, ограничения, альтернативы. При этом они должны
измерять их характеристики, чтобы в дальнейшем оценить и сравнить
рассматриваемые варианты (альтернативы, объекты, способы действия) и
осуществить целенаправленный выбор среди них лучшего или приемлемого
варианта (вариантов), основываясь на субъективных предпочтениях.
Предпочтения ЛПР — одна из главных составляющих задачи принятия
решения. Будем называть предпочтением ЛПР выраженное каким-либо
образом его личное суждение о наличии или отсутствии преимущества
одного из вариантов по отношению к другому варианту или ко всем
остальным вариантам, либо в целом, либо по некоторым отдельным
характеристикам.
Субъективность предпочтений не означает, что ЛПР может поступать, как
ему заблагорассудится. В реальных ситуациях выбора человек обычно
ведет себя достаточно разумно, его поведение и действия подчиняются
некоторому внутреннему принципу рациональности.
При этом разные люди могут иметь свои собственные системы ценностей,
свои различные представления о предпочтительности.
44
44.
Пример 0 (реляционная модель предпочтений).Семья решила купить дом. Обсудив, определили 6 критериев, которым
должен удовлетворять дом:
К1 – общая площадь (м2);
К2 – земельный участок (м2);
К3 – инфраструктура, экология;
К4 – транспортные удобства (0-10 баллов, наилучшее значение 10 баллов);
К5 – потребность в ремонте;
К6 – цена дома (млн. руб.).
Из всего множества вариантов семья остановилась на 7 вариантах
покупаемого дома Д1-Д7. Необходимо из них выбрать наилучший.
Д1 Д 7
Д3 Д2
Д3 Д5
Д4 Д6
Д1
Д2
К1
120
70
К2
200
100
К3
отлично
плохо
К4
6
5
Д3
Д4
Д5
90
67
81
300
600
290
отлично
отлично
хорошо
10
5
6
Д6
65
600
удовлетв.
3
Д7
110
100
плохо
5
К5
новый дом
косметический
ремонт
новый дом
новый дом
капитальный
ремонт
капитальный
ремонт
новый дом
К6
7,8
3,9
3,9
3,6
4,1
3,6
45
8,4
45.
Для реализации возможности использования предпочтений ЛПР в процессепринятия решения необходимо располагать информацией о них, т.е.
описать и/или измерить предпочтения ЛПР.
Измерения могут быть
качественными или количественными,
объективными или субъективными.
Качественные предпочтения описывают только факт превосходства
(строгого или нестрогого) одной альтернативы над другой без указания
силы этого превосходства, количественные – выражают не только факт
предпочтения, но и его силу.
Измерение – процедура сравнения объектов по определённым показателям
(числам, символам или номерам).
Объектами измерения могут быть предметы, явления, события,
альтернативы (решения), критерии и т.п.
Показатели сравнения объектов – это свойства объектов.
46
46.
В ТПР употребляются разные модели формализации предпочтений ЛПР:o реляционная модель предпочтений, основанная на бинарных
отношениях;
o функциональная модель — предпочтительность варианта для ЛПР
выражается значением некоторой числовой функции, зависящей от
характеристик рассматриваемого варианта (целевые функции,
показатели эффективности, функции ценности или полезности и т.п.) .
Например, в реляционной модели отношение тождества между объектами
А, В и С удовлетворяет следующим аксиомам:
1)
А = В либо А ≠ В;
2)
Если А = В, то В = А (симметрия);
3)
Если А = В и В = С, то А = С (транзитивность).
Кроме тождества существуют много других отношений между объектами:
o «больше» или
«меньше»
o «хуже», «лучше» или «не хуже», «не лучше»
o «предпочтительнее» и т.д.
Различными являются также способы сравнения объектов:
o сравнение объектов с одним эталоном;
o сравнение объектов друг с другом и т.п.
47
47.
Пример 0 (реляционная модель предпочтений).Семья решила купить дом. Обсудив, определили 6 критериев, которым
должен удовлетворять дом:
К1 – общая площадь (м2);
К2 – земельный участок (м2);
К3 – инфраструктура, экология;
К4 – транспортные удобства (0-10 баллов, наилучшее значение 10 баллов);
К5 – потребность в ремонте;
К6 – цена дома (млн. руб.).
Из всего множества вариантов семья остановилась на 7 вариантах
покупаемого дома Д1-Д7. Необходимо из них выбрать наилучший.
Д1 Д 7
Д3 Д2
Д3 Д5
Д4 Д6
Д1
Д2
К1
120
70
К2
200
100
К3
отлично
плохо
К4
6
5
Д3
Д4
Д5
90
67
81
300
600
290
отлично
отлично
хорошо
10
5
6
Д6
65
600
удовлетв.
3
Д7
110
100
плохо
5
К5
новый дом
косметический
ремонт
новый дом
новый дом
капитальный
ремонт
капитальный
ремонт
новый дом
К6
7,8
3,9
3,9
3,6
4,1
3,6
48
8,4
48.
Пример 1 (функциональная модель).На складе фирмы имеется 50 м3 дерева и 54 м3 металла. Из этого сырья
можно производить дачную мебель двух видов: столы и стулья. Для
изготовления одного стола требуется 10 ед. дерева и 6 ед. металла, а для
изготовления одного стула - 5 ед. дерева и 9 ед. металла. Продажная цена
одного стола составляет 8 условных денежных единиц, а одного стула – 6 у.е.
При производстве первого изделия образуется 10 ед. вредных отходов, а
при производстве второго 5 ед. Продукция первого вида (столы) поставляется
на экспорт. Хотя на прибыли это и не сказывается, компания из стратегических
соображений заинтересована в увеличении производства таких изделий.
Требуется найти оптимальное решение для производства данной мебели,
т.е. максимизировать доход, уложившись при этом в имеющиеся ресурсы,
минимизировать количество отходов и определить какое количество столов
поставлять на экспорт?
u1 ( x1 , x2 ) 8 x1 6 x2 max,
u2 ( x1 , x2 ) 10 x1 5 x2 min,
u3 ( x1 , x2 ) x1 max,
10 x1 5 x2 50,
6 x1 9 x2 54,
x1 , x2 0.
Оптимальные решения по каждому критерию в отдельности:
u1{x1=3; x2=4}; u2{x1=0; x2=0}; u3{x1=5; x2=0};
49
49.
Чтобы сравнивать показатели (свойства) объектов измерения и отношениямежду ними, вводится понятие эмпирической системы – своего рода
модель эксперта (эмпирический (от греч. Empeirikos) полученный из
опыта, опирающийся на реальные факты, априорный):
M = <X, R>,
где X = {x1, x2,…, xm } – множество объектов измерения;
R = {r1, r2,…rs } – множество отношений между объектами Х.
Функция – это частный случай отношения. Запись вида xi R xj означает, что
объекты xi и xj находятся между собой в бинарном отношении R.
Если все объекты Х между собой сравнимы, то бинарное отношение
является полным (совершенным, линейным), иначе – неполным
(несовершенным, нелинейным).
Полное и неполное отношения могут обладать следующими свойствами:
o рефлексивность (x R x);
o антирефлексивность (если x R y, то x≠y, если R не отношение
тождества);
o симметричность (если x R y, то y R x);
o антисимметричность (если x R y и y R x, то x=y);
o транзитивность (если x R y и y R z, то x R z).
Одним из наиболее часто применяемых инструментариев в ТПР является
реляционная модель предпочтений, основанная на бинарных отношениях
50
50.
Однако на практике при реальных измерениях в эмпирических системахобъекты, показатели их сравнения и виды отношений, весьма разнообразны.
Для унифицирования процесса измерения используют универсальную
числовую систему
N = (C, S),
где С множество действительных чисел; S – множество отношений между
числами.
Но для этого универсальная числовая система должна быть изоморфной:
системы изоморфны, если они подобны и существует взаимно однозначное
отображение F объектов измерения одной системы в другую, т.е. отношения
F
предпочтения сохраняются: M X, R
N C, S
Всегда существует числовая система N
для описания эмпирических объектов,
если между ними существуют
отношения тождественности, строгого
или нестрогого порядка.
Эмпирическую систему М представляют
соответствующими типами шкал
измерений.
51
51.
В теории измерений существуют три фундаментальные методологическиепроблемы:
1) проблема существования (измеримости),
2) проблема единственности,
3) проблема адекватности.
Проблема существования состоит в получении ответа на принципиальный
вопрос: возможно ли вообще непротиворечивое отображение данной
эмпирической системы на числовую ось? Если, например, некоторое
качественное отношение не является транзитивным, то измерить его
невозможно.
Проблема единственности. Даже если эмпирическая система измерима, то
единственно ли её отображение на числовую ось? Как правило, оно
неоднозначно – измерение производится с точностью до множества
преобразований F. И эта неопределённость даёт возможность построить
классификацию шкал измерений.
Проблема адекватности. Выполнив измерения эмпирической системы и
получив выборку значений на числовой оси эксперт обычно производит
над ними математические операции с целью получения результатов, ради
которых организовывалась экспертиза. В связи с этим возникает вопрос:
какие операции разрешается проводить над измерениями, чтобы
результаты были разумными (адекватными)?
52
52.
Шкала измерений – это числовая ось, показывающая как элементымножеств отображаются в числа.
Необходимость использования шкал измерения в теории принятия
решений связано с потребностью агрегирования мнений экспертов,
построения обобщённых показателей и рейтингов. В соответствии с
теорией измерений при математическом моделировании реального
явления или процесса следует прежде всего установить типы шкал, в
которых измерены те или иные переменные.
Тип шкалы задаёт группу допустимых преобразований шкалы.
Допустимые преобразования не меняют соотношений между объектами
измерения. Например, при измерении длины переход от аршин к метрам
не меняет соотношений между длинами рассматриваемых объектов –
если первый объект длиннее второго, то это будет установлено и при
измерении в аршинах, и при измерении в метрах.
Информации в количественной шкале достаточно для ее
отображения в качественную шкалу. Обратное не верно.
Качественные
шкалы
Номинальная
шкала
Шкала
порядков
Количественные
шкалы
Шкала
интервалов
Шкала
отношений
Шкала
разностей
Абсолютная
шкала
53
53.
Номинальная шкала (шкала наименований) служит для различенияобъектов, указания принадлежности объекта некоторому классу.
Объектам одного класса присваивается одно число или имя, а объектам
разных классов – разные числа или имена. В этой шкале числа если и
используются, то лишь как метки.
Допустимыми являются все взаимнооднозначные преобразования.
В номинальной шкале нет масштаба и точки отсчёта.
Для компьютерной обработки данных в этой шкале используют только
операцию их совпадения или несовпадения. Операция включает подсчёт
числа или частоты совпадений.
Степень различия объектов по шкале определить невозможно.
В номинальной шкале измерены, например, почтовые индексы, номера
телефонов, автомашин, паспортов, студенческих билетов, номера
страховых свидетельств, ИНН и т.д.
Пол людей тоже измерен в шкале наименований, результат измерения
принимает два (в мире – три) значения – мужской, женский. Раса,
национальность, цвет глаз, волос, характер, и т.п. – это номинальные
признаки.
54
54.
Шкала порядков (порядковая шкала) используется для измеренияпредпочтения одного объекта перед другим (ранжирования).
Как показали многочисленные опыты, человек более правильно (и с
меньшими затруднениями) отвечает на вопросы качественного
(сравнительного) характера, чем количественного. Эта шкала широко
используется при экспертном оценивании расстояния между парой объектов.
В порядковой шкале допустимыми являются все строго возрастающие
преобразования.
Разновидности порядковой шкалы: ранговые и балльные шкалы.
В этой шкале числа используются не только для различения объектов, но и
для установления порядка между объектами. Числа в шкале определяют
порядок следования объектов, но не степень предпочтения.
Разновидностью порядковой шкалы также считается полярная шкала,
которая используется для различения полюсов («холодно – жарко», «белое –
черное», «за – против», {– 1; +1} и т.п.) и имеет середину.
55
55.
В минералогии используется шкала Мооса, по которому минералыклассифицируются согласно критерию твёрдости: тальк – 1, гипс – 2,
кальций – 3, флюорит – 4, апатит – 5, ортоклаз – 6, кварц – 7, топаз – 8,
корунд – 9, алмаз – 10. Минерал с большим номером является более
твёрдым, чем минерал с меньшим номером, при нажатии царапает его.
Бофортова шкала ветров («штиль», «слабый ветер», «умеренный ветер»
и т.д.), шкала силы землетрясений. Очевидно, нельзя утверждать, что
землетрясение в 2 балла (лампочка качнулась под потолком) ровно
в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего
на поверхности земли).
В медицине порядковыми шкалами являются – шкала стадий
гипертонической болезни (по Мясникову), шкала степеней сердечной
недостаточности (по Стражеско-Василенко-Лангу), шкала степени
выраженности коронарной недостаточности (по Фогельсону), и т.д.
Все эти шкалы построены по схеме: заболевание не обнаружено; первая
стадия заболевания; вторая стадия; третья стадия и т.д.
Каждая стадия имеет свойственную только ей медицинскую характеристику.
56
56.
Шкала интервалов определяет величину различий между объектами впроявлении свойства. С помощью шкалы интервалов можно сравнивать
два объекта. При этом выясняют, насколько более или менее выражено
определённое свойство у одного объекта, чем у другого.
Шкала интервалов имеет масштабную единицу, но положение нуля
(точки отсчёта) на ней произвольно.
Величины, измеряемые в этой шкале, зависят от начала отсчёта.
Допустимыми преобразованиями в шкале интервалов являются
линейные возрастающие преобразования, т.е. мы имеем право изменять
масштаб шкалы, умножая каждое из ее значений на константу, и
производить ее сдвиг относительно произвольно выбранной точки на
любое расстояние вправо или влево (прибавлять или отнимать
константу).
Температурные шкалы Цельсия и Фаренгейта связаны именно такой
зависимостью: С = 5/9 *(F - 32). Можно не только сказать, что
температура 40 градусов выше, чем температура 30 градусов, но и что
увеличение температуры с 20 до 40 градусов вдвое больше увеличения
температуры от 30 до 40 градусов.
57
57.
Шкала разностей или периодическая шкала являются частным случаемшкалы интервалов.
В этой шкале есть естественная единица измерения, но нет
естественного начала отсчёта.
Время измеряется по шкале разностей. На современном уровне знаний
естественного начала отсчёта указать нельзя. Дату сотворения мира
различные авторы рассчитывают по-разному, равно как и момент
рождества Христова.
58
58.
Шкала отношений.В ней есть естественное начало отсчёта – нуль, но нет естественной
единицы измерения.
По этой шкале можно получить такие данные о выраженности свойств
объектов можно сказать, во сколько раз один объект больше или
меньше другого.
Допустимыми преобразованиями в шкале отношений являются
подобные (изменяющие только масштаб), т.е. линейные возрастающие
преобразования без свободного члена.
По шкале отношений измерены большинство физических единиц: масса
тела, длина, заряд, деньги, цены в экономике.
Примерами являются шкала температур Кельвина, пересчёт цен из
одной валюты в другую по фиксированному курсу.
59
59.
Абсолютная шкала.Только для этой шкалы результаты измерений – числа в обычном смысле
слова. Примером является число людей в комнате.
Для абсолютной шкалы допустимым является только тождественное
преобразование. (Если в аудитории сидит 100 человек, то это число
изменить невозможно.)
В процессе развития соответствующей области знания тип шкалы может
меняться. Так, сначала температура измерялась по порядковой шкале
(холоднее – теплее). Затем – по интервальной (шкалы Цельсия,
Фаренгейта, Реомюра). Наконец, после открытия абсолютного нуля
температуру можно считать измеренной по шкале отношений (шкала
Кельвина).
60
60.
Обработка результатов измеренийВ большинстве случаев
обработка результатов
экспертиз (измерений,
характеристик) сводится к
получению осредненных
(агрегированных ) значений.
Проводить осреднение
допускается только для
однородных характеристик,
измеренных в одной шкале –
или оценки различных
измерений одной и той же
характеристики, или оценки
нескольких различных
однородных характеристик.
В таблице ci – это вес
(важность, ценность, степень
доверия, компетенции)
оценки, измерения.
61
61.
Медиана (квантиль 50%) – это значение признака, которое лежит в основеранжированного ряда и делит этот ряд на две равные по численности части.
62
62.
Простая и взвешенные средние величины различаются не только по величине (не всегда), поспособу вычисления, но и по своей роли в решении задач принятия решения. При этом
средневзвешенные величины используются для сравнения объектов с учётом вклада
различных факторов в осреднённую оценку (отражается весовыми коэффициентами
важности ci). Сводные данные по характеристикам разных шкал и перечень допустимых
операций осреднения характеристик приведены в таблице.
63
63.
Стандартным способом перехода от первичных измерений к инвариантнымв шкале интервалов является нормализация по размаху выборки, при
которой каждое измерение преобразуется по формуле
xi min
xi
i
~
xi
max xi min
xi
i
.
i
В шкале отношений для перехода от первичных измерений к
инвариантным используют нормирование:
— нормирование по наибольшему значению:
~
xi
xi
.
max xi
i
Наибольшее нормализованное значение становится равным единице,
наименьшее значение не определено.
— нормирование по сумме:
~
xi
xi
x
.
i
Наибольшее и наименьшие значенияi не определены, но сумма элементов
выборки всегда равна единице.
64
64.
— нормирование по евклидовой норме:xi
xi
n
.
2
x
i
i 1
Наибольшее и наименьшие значения не определены.
ВАЖНО: Как до нормировки, так и после неё, наилучшее/наихудшее
значение должно сохранить свою позицию (ранг).
65
65.
2. Методы субъективных измерений в ТПРМетоды субъективных измерений в ТПР предполагают, что дано
конечное число измеряемых объектов X={x1, x2, …, xn} и
сформулированы один или несколько признаков, по которым они
сравниваются. Методы различаются только процедурой сравнения.
На практике применяют следующие методы субъективных измерений:
ранжирование;
парное (попарное) сравнение;
непосредственная оценка;
последовательное сравнение (метод Чёрчмена-Акоффа).
66
66.
Ранжирование это различные процедуры измерения дляупорядочения объектов в порядке предпочтений эксперта или ЛПР.
Если между объектами нет одинаковых, то это означает строгий
порядок:
x1 x2 ... xn
(Знак это знак строгого предпочтения, означающий «больше» в
количественной шкале, «лучше» в качественной шкале.
Знак это знак нестрогого предпочтения, означающий «не меньше»
в количественной шкале, «не хуже» в качественной шкале.)
Тогда ранжированию объектов в порядковой шкале соответствуют
упорядоченные числа (ранги):
c1 c2 ... cn
Если некоторые объекты тождественны, то это означает нестрогий
порядок.
67
67.
2.1. Метод непосредственной оценкиМетод представляет собой процедуру приписывания объектам числовых
значений в выбранной шкале порядка или интервалов. В качестве таких шкал
используются, например, 5-, 10-, 100-балльные и др. шкалы.
Первоначально все оцениваемые объекты целесообразно упорядочить по
важности для ЛПР, т.е. установить ранжирование.
Согласно данному ранжированию по выбранной шкале каждому объекту
оценки назначают числовое значение, причем чем важнее (ценнее) объект,
тем больше должно быть значение. Обязательно необходимо соблюдать
свойство транзитивности назначаемых значений.
После того как всем объектам назначены значения
важности, то в зависимости от поставленной задачи
или используемого метода многокритериального
оценивания (оптимизации) данные значения
непосредственно используются далее либо
осуществляют их нормировку, например, по сумме.
Если этот метод применяется для групповой оценки, то агрегированная
оценка отдельного объекта получается путем осреднения всех оценок этого
объекта выставленных всеми экспертами – среднеарифметическое,
среднегеометрическое, среднеквадратичное, среднегармоническое и др. А уже
осредненные оценки при необходимости затем нормируются по сумме.
68
68.
Пример 2. Семья решила купить дом. Обсудив, определили 6 критериев,которым должен удовлетворять дом, из которых оставили четыре :
К1 – общая площадь (м2);
К2 – земельный участок (м2);
К4 – транспортные удобства (0-10 баллов, наилучшее значение 10 баллов);
К6 – цена дома (млн. руб.).
Необходимо методом непосредственной оценки определить веса важности
критериев, которые должны быть нормированы для дальнейшего
использования.
Решение.
Пусть семья ранжировала критерии по важности для нее следующим
образом:
К
К
К К
6
4
1
2
Тогда, исходя из данного ранжирования, после обсуждения каждому
критерию было назначено численное значение важности по 10-балльной
шкале:
w6=9, w4=6, w1=4, w2=4.
Тогда нормированные значения весов важности:
w6=9/23, w4=6/23, w1=4/23, w2=4/23.
69
69.
2.2 Метод простого ранжированияПусть имеется m экспертов. Поставлена задача провести ранжирование n
объектов. Результатом ранжирования будет матрица (m x n), в которой
ранги определяют только порядок объектов, а не то, насколько один объект
предпочтительнее другого. Для ее построения каждый эксперт расставляет
объекты в порядке их важности для него. При этом цифрой 1 обозначают
наиболее важный объект, 2 – следующий по степени важности и т.д. до n.
Далее, объект, обозначенный цифрой 1, получает n баллов, объект 2 –
(n -1) баллов и т.д. до 1 балла у объекта с цифрой n. Эти оценки заносятся
в соответствующую строку матрицы – строку оценок эксперта. Тогда для
построения итогового ранжирования вычисляем значения важности каждого
объекта по формуле
m
cij
w j n i 1 m
, j 1,2,..., n,
cij
j 1
i 1
cij - оценка j-го объекта у i-го эксперта.
Объект с наибольшим значением w j получает наивысший ранг,
далее - по убыванию.
В этом методе мы переходим от шкалы порядка к шкале _________?
70
70.
Пример 3. Имеется 4 объекта xi. Экспертиза проводится 4 экспертами:1-й x2 x1 x4 x3 , 2-й x1 x2 x3 x4 , 3-й x1 x3 x2 x4 , 4-й x4 x1 x2 x3 .
Решение.
По результатам экспертизы построена матрица (уже в баллах):
Номер
эксперта
x1
x2
x3
x4
1
3
4
1
2
2
4
3
2
1
3
4
2
3
1
4
3
2
1
4
3 4 4 3 14
w1
;
40
40
1 2 3 1 7
w3
;
40
40
x1 x2 x4 x3
4 3 2 2 11
w2
;
40
40
2 1 1 4 8
w4
.
40
40
Достоинство метода простота. Недостатки трудность ранжирования
большого числа объектов ( n 10 ), т.к. число связей объектов быстро
растет, что влечет ошибки в процессе ранжирования; в начале
процедуры метода используется только строгое упорядочение.
71
71.
2.3 Попарное сравнение по абсолютной важностиПопарное (парное) сравнение, как и ранжирование, проводится в
порядковой шкале, но путём сравнения всех возможных пар объектов. Для
этого используются разные формы числового представления.
Строится матрица C cij n n парных сравнений объектов x1 , x2 ,..., xn
важности (предпочтительности ) для ЛПР. Элементы этой матрицы
отражают предпочтения ЛПР следующим образом:
cij 1, если
xi x j
cij 0, если
xi x j
или
cij 2, если
xi x j
cij 1, если
xi x j
cij 0, если
xi x j
по их
Тогда ранги объектов можно установить по формуле:
wi
ci
n
ci
n
, ci cij
j 1
i 1
Объект с наибольшим значением wi получает наивысший ранг,
далее по убыванию
72
72.
Если m экспертов выполняют экспертизу в соответствии с методомпопарного сравнения по абсолютной важности, которые заполнены в
соответствии с правилом
Aij 1, если
fi f j
Aij 0, если
fi f j
То имеется m матриц парных сравнений Ak Aijk . Чтобы на их основе
получить агрегированную оценку групповой оценки и осуществить либо
ранжирование объектов, либо выбор наилучшего объекта (альтернативы),
необходимо выполнить следующие действия:
1. Получение суммарной матрицы парных сравнений – соответствующие
элементы каждой матрицы парных сравнений суммируются A Aij .
2. Для матрицы п. 1 выполняем ее приведение по формуле
~
Aij 1, если
Aij m / 2
~
Aij 0, если
Aij m / 2
3. Для приведенной матрицы вычисляем числовые значения, по которым
осуществляем ранжирование
~
m
Ai
~
~
wi m
, Ai Aij
~
j 1
A
i
i 1
73
73.
Пример 4. Семья решила купить дом. Обсудив, определили 6 критериев,которым должен удовлетворять дом, из которых оставили четыре :
К1 – общая площадь (м2);
К2 – земельный участок (м2);
К4 – транспортные удобства (0-10 баллов, наилучшее значение 10 баллов);
К6 – цена дома (млн. руб.).
Необходимо определить веса важности этих критериев методом попарного
сравнения по абсолютной.
К6
Решение.
К2
К4
К1
К1
Парные сравнения родителей
К1
1
1
1
1
К1
К2
К4
К6
К2
0
1
0
1
К4
0
1
1
1
К1
2
1
1
1
К2
1
2
1
2
К4
1
1
2
1
К6
1
0
1
2
К6
К2
Парные сравнения детей
К6
0
0
0
1
К1
1
0
0
0
К1
К2
К4
К6
Суммарная матрица
К1
К2
К4
К6
К4
К2
1
1
1
1
К4
1
0
1
0
К6
1
0
1
1
Приведенная матрица
~
Aij 1, если
~
Aij 0, если
A m/2
ij
Aij m / 2
К1
К2
К4
К6
Тогда нормированные значения весов важности:
w6=4/15, w4=4/15, w1=4/15, w2=3/15.
К1
1
1
1
1
К2
1
1
1
1
К4
1
1
1
1
К6
1
0
1
1
сумма
4
3
4
4
0,266667
0,2
0,266667
0,266667
74
74.
2.4. Попарное сравнение по относительной важностиЭтот подход является частью метода анализа иерархии (МАИ).
Сравниваемые элементы первоначально попарно сравниваются друг с
другом по относительной важности (степени предпочтения).
Таким образом, необходимо вербальную (качественную) оценку
предпочтения перевести в численную (количественную).
Полученные парные сравнения составляют массив чисел, который
оформляется в виде матрицы сравнения, по которой затем по определенной
процедуре вычисляют веса важности, ценности.
75
75.
2.5. Метод У. Чёрчмена – Л. Акоффа: последовательное сравнение по суммарнойважности
Сущность метода проще уяснить, если воспользоваться такой физической
аналогией: представим себе, что имеются несколько предметов и
рычажные весы без гирь, позволяющие узнать, содержимое какой из
чашек весов тяжелее. Здесь объем (вес) предмета соответствует его
важности.
76
76.
Метод Чёрчмена-Акофа описывается следующим алгоритмом, справедливым присравнении альтернатив, объектов, критериев и т.п. Для упрощения обозначений
одновременное рассмотрение сравниваемых вариантов обозначается знаком «+».
Рассмотрим алгоритм на примере сравнения критериев.
Шаг 1. Критерии упорядочиваются по убыванию предпочтения:
К1
К2
К3 ... К n 1
Кn
Шаг 2. Критериям приписываются произвольные оценки (полезности), значения
которых убывают в соответствии с упорядочением:
u1 u 2 u 3 ... u n 1 u n
Шаг 3. Эксперту задаётся ряд вопросов вида «что предпочтительнее:
критерий К1 или логическая сумма (К2 + К3 + … Кn)?». Вопросы и
соответствующие им ответы упорядочены в виде таблицы (см. слайд выше), они
задаются по колонкам: 1-я, 2-я и т.д. Если вместо «или» эксперт ставит ≺, то
задаётся следующий вопрос из этой же колонки, но уже с удаленным в последней
правой части критерием. А если эксперт отвечает , то происходит переход к
началу следующей колонки – сравнение следующего по важности критерия с
оставшимися с аналогичным удалением по одному критерию, начиная с
последнего.
В физической интерпретации это означает, что на левой чашке весов всегда находится один
критерий, а на правой — ряд меньших по «весу», причём переход к следующему взвешиванию в
той же колонке соответствует удалению из правой чашки самого «лёгкой» (незначимого) критерия.
Всегда на правой чаше должно быть не менее двух критериев.
77
77.
Шаг 4. Ответы на вопросы просматриваются в обратном порядке.Одновременно корректируются оценки ui для того, чтобы обеспечить
сохранение выявленного в ответах качественного сравнения с
количественными с учетом их полезностей.
Шаг 5. С помощью масштабного преобразования приводят оценки важности
к желаемому интервалу. Но обычно осуществляют нормирование по сумме
u
u~i i .
ui
i
78
78.
Пример 5. Семья решила купить дом. Обсудив, определили 6 критериев,которым должен удовлетворять дом:
К1 – общая площадь (м2);
К2 – земельный участок (м2);
К3 – инфраструктура, экология;
К4 – транспортные удобства (0-10 баллов, наилучшее значение 10 баллов);
К5 – потребность в ремонте;
К6 – цена дома (млн. руб.).
Необходимо определить веса важности критериев методом У. Чёрчмена –
Л. Акоффа.
Решение.
Шаг 1. Пусть семья ранжировала критерии по важности для нее
следующим образом:
К6
К4
К3
К1
К5
К2
Шаг 2. Припишем критериям не противоречащие их ранжированию
произвольные начальные значения полезностей:
u(К6) = 10, u(К4) = 8, u(К3) = 5, u(К1) = 3, u(К5) = 2, u(К2) = 2.
79
79.
Шаг 3. Задавая эксперту вопросы в соответствии с установленными правилами,получаем следующую таблицу ответов. Цифры в скобках обозначают порядковый
номер ответа.
(1) К 6
К 4 К3 К1 К 5 К 2 (5) К 4
К3 К1 К 5 К 2 (7) К3
К1 К5 К 2
(2) К 6
К 4 К 3 К1 К 5
К3 К1 К5
К1 К 5
(3) К 6
К 4 К3 К1
(4) К 6
К 4 К3
(6) К 4
(8) К3
(9) К1
К5 К 2
Шаг 4. Просматриваем ответы в обратном порядке и проверяем выполнение
неравенств относительно полезностей, отражающих множественные сравнения.
Если неравенство не выполняется, корректируем его левую часть.
u(К6) = 10, u(К4) = 8, u(К3) = 5, u(К1) = 3, u(К5) = 2, u(К2) = 2.
Номер
ответа
Неравенство для
полезностей
Выполняется
(9)
3 < 2+2
Да
(8)
5 ≥ 3+2
Да
(7)
5 < 3+2+2
Да
(6)
8 ≥ 5+3+2
Нет
(5)
10 < 5+3+2+2
Да
(4)
10 ≥ 10+5
Нет
Корректировка
u(К4) = 10
u(К6) = 15
80
80.
Текущие полезности: u(К6) = 15, u(К4) = 10, u(К3) = 5, u(К1) = 3, u(К5) = 2, u(К2) = 2.Номер
ответа
Неравенство для
полезностей
Выполняется
(9)
3 < 2+2
Да
(8)
5 ≥ 3+2
Да
(7)
5 < 3+2+2
Да
(6)
8 ≥ 5+3+2
Нет
(5)
10 < 5+3+2+2
Да
(4)
10 ≥ 10+5
Нет
(3)
15 < 10+5+3
Да
(2)
15 < 10+5+3+2
Да
(1)
15 < 10+5+3+2+2
Да
Корректировка
u(К4) = 10
u(К6) = 15
81
81.
Шаг 5. В результате двух корректировок имеем скорректированныеполезности критериев:
u(К6) = 15, u(К4) = 10, u(К3) = 5, u(К1) = 3, u(К5) = 2, u(К2) = 2.
Разделив полученные числа на их сумму, получаем нормированные оценки:
~u(К ) = 15/37 0,41; u(К
~ ) = 10/37 0,27; ~u(К ) = 5/37 0,14;
6
4
3
~
~
~
u(К1) = 3/37 0,08; u(К5) = u(К2) = 2/37 0,05,
соответствующие весам важности (ценности) критериев с точки зрения
эксперта, измеренные в шкале отношений.
82
82.
2.6. Декомпозиция критериев. Определение весов важности субкритериевЗачастую реальные задачи многокритериального оценивания имеют очень
большое количество критериев, по которым оцениваются альтернативы. Это
порождает сложности адекватной оценки их весов важности (ценности) для
ЛПР или экспертов. Причем сложности как вычислительные, так и
непосредственно оценки.
В этой ситуации целесообразно множество критериев разбивать на группы:
групповые критерии – критерии 1-го уровня иерархии, которые в свою
очередь состоят из субкритериев – критериев 2-го уровня.
Итак, имеем небольшое количество критериев 1-го уровня, каждый из
которых в свою очередь, как правило, состоит из небольшого количества
субкритериев.
Задача
Критерий 1
Критерий 2
Критерий 3
Субкритерий 21
Субкритерий 31
Субкритерий 22
Субкритерий 32
Субкритерий 11
Субкритерий 12
Субкритерий 33
Субкритерий 13
83
83.
Тогда можем отдельно определить веса важности критериев 1-го уровняиерархии – любым из рассмотренных выше методов. Далее для каждой
группы субкритериев аналогично определяем веса важности критериев 2-го
уровня иерархии – любым из рассмотренных выше методов. И в заключении
необходимо пересчитать веса важности субкритериев так, что сумма их весов
была равна весу важности соответствующего группового критерия по
формуле
wij wi
cij
cij
j
Здесь wij – глобальный вес j-го субкритерия из i-й группы, wi – глобальный
вес критерия 1-го уровня i-й группы, cij – локальный вес j-го субкритерия
из i-й группы.
84
84.
Пример 6. Рассмотрим фрагмент задачи многокритериального оцениваниятехнологических проектов замены угольных электростанций на электростанции
на природном газе.
Критерии 1-го и 2-го уровней представлены в таблице.
Критерии 1-го
уровня
Оценка
важности
критерия
1-го
уровня
Вес
критерия
1-го
уровня
Критерии 2-го уровня
Технические
характеристики
технологии (К1)
Адаптивность (К11)
Эффективность сжигания
газа (К12)
Надежность (К13)
Потребление
ресурсов и
энергии (К2)
Потребление воды (К21)
Потребление энергии
(К22)
Потребление пара (К23)
Уровень
загрязнения (К3)
Уровень твердых
выбросов (К31)
Уровень ядовитых газов
(К32)
Уровень СО2 (К33)
Экономическая
эффективность
(К4)
Стоимость проекта (К41)
Рентабельность проекта
(К42)
Оценки
важности
критериев 2го уровня
Веса
критериев
2-го уровня
85
85.
Допустим, что по отдельности оценку важности критериев 1-го и 2-го уровняопределяем методом непосредственной оценки по 5-и балльной шкале, т.е.
отдельно оцениваем важность критериев 1-го уровня – заполняем второй
столбец, а также по отдельности в каждой группе оцениваем важность
критериев 2-го уровня в рамках своей группы – заполняем пятый столбец:
Критерии 1-го
уровня
Оценка
важности
критерия
1-го
уровня
Технические
характеристики
технологии (К1)
4,6
Потребление
ресурсов и
энергии (К2)
Уровень
загрязнения (К3)
Экономическая
эффективность
(К4)
3,1
4,8
4,2
Вес
критерия
1-го
уровня
Критерии 2-го уровня
Оценки
важности
критериев 2го уровня
Адаптивность (К11)
Эффективность сжигания
газа (К12)
Надежность (К13)
3,7
2,3
Потребление воды (К21)
Потребление энергии
(К22)
Потребление пара (К23)
4,5
4,6
Уровень твердых
выбросов (К31)
Уровень ядовитых газов
(К32)
Уровень СО2 (К33)
3,4
Стоимость проекта (К41)
Рентабельность проекта
(К42)
4,5
4,5
Веса
критериев
2-го уровня
3
3,1
4,2
4,8
86
86.
Тогда веса важности критериев 1-го уровня определим путем нормировки посумме – третий столбец, а веса критериев 2-го уровня пересчитаем по формуле:
wij wi
cij
cij
j
Критерии 1-го
уровня
Оценка
важности
критерия
1-го
уровня
Веса
критериев
1-го уровня
Критерии 2-го уровня
Оценки
важности
критериев
2-го уровня
Технические
характеристики
технологии (К1)
4,6
4,6/16,7=
0,27
Адаптивность (К11)
Эффективность сжигания
газа (К12)
Надежность (К13)
3,7
2,3
0,27*3,7/(3,7+2,3+3)=0,11
3
0,09
Потребление воды (К21)
Потребление энергии
(К22)
Потребление пара (К23)
4,5
3,7
0,08
0,06
3,1
0,05
Уровень твердых
выбросов (К31)
Уровень ядовитых газов
(К32)
Уровень СО2 (К33)
3,4
0,08
4,2
0,1
4,8
0,11
Стоимость проекта (К41)
Рентабельность проекта
(К42)
4,2
4,8
0,12
0,13
Потребление
ресурсов и
энергии (К2)
Уровень
загрязнения (К3)
3,1
4,8
3,1/16,7=
0,19
4,8/16,7=
0,29
Экономическая
эффективность
(К4)
4,2
4,2/16,7=
0,25
Сумма
16,7
1
Веса
критериев 2-го
уровня
0,07
1
87
87.
Южный федеральный университетИнститут компьютерных технологий и информационной безопасности
Презентация к лекциям №3-5
по дисциплине
«Теория принятия решений»
Лектор:
к.т.н., доцент каф. СиПУ
Кузьменко А.А.
andrew.kuzmenkosipu@gmail.com
88.
Лекции №3-5 Оптимальный выбор в условияхпротивоборства: теория игр в задачах принятия
решений.
Цели лекций:
- дать представление об игровом подходе к рациональному
выбору решений в условиях противоборства,
- познакомить с фундаментальными понятиями и результатами
теории игр,
- изучить методы решения матричных игр.
Содержание лекций:
1. Основные понятия и определения, классификация игр.
2. Нормальная форма матричной игры.
3. Игры со строгим соперничеством: принципы принятия решений
3.1 Игры с седловой точкой.
3.2 Игры без седловой точки.
4. Геометрическое решение игр в смешанных стратегиях.
5. Решение игр методом последовательных приближений.
6. Решение игр в смешанных стратегиях методом линейного
программирования.
7. Решение биматричных игр (общий подход).
8. Другие направления теории игр (обзор).
89
89.
1. Основные понятия и определения, классификация игрВ отличие от ситуаций игры с природой, которая безразлична к исходам
решений, может иметь место ситуация, когда неконтролируемые факторы
сосредоточены в руках разумного противника: ЛПР-2, который имеет свою
точку зрения на полезности исходов, отличающуюся от предпочтений ЛПР-1.
В 1944 году вышел знаменитый труд Дж. фон Неймана и О. Моргенштерна
«Теория игр и экономическое поведение», где теорию игр впервые
применили для решения бизнес-задач с неполной информацией.
1960-е годы были временем экспериментов и революционных знаний,
полученных Джоном Нэшем и Л. Гурвичем. Однако первая Нобелевская
премия по теории игр была присуждена только в 1994 г. Дж. Нэшу.
В 2007 г. Нобелевскую премию получили Гурвич, Майерсон и Маскин
«… за первопроходческий вклад в теорию игр и принятие решений».
Сейчас теория игр очень популярна для решения разнообразных
экономических задач (аукционы, реклама, производство в условиях
конкуренции, конфликты и др.), задач обеспечения информационной
безопасности.
90
90.
Если предпочтения сторон, управляющих выбором, не совпадают, возникаетконфликтная ситуация. Типичными примерами конфликтных ситуаций
являются войны, столкновения интересов в рыночной конкуренции,
спортивные соревнования и т.п.
Теория игр (ТИ) является математической теорией конфликтных ситуаций,
при помощи которой можно выработать рекомендации по рациональному
образу действий участников конфликта. ТИ, как части нормативной ТПР, в
дескриптивной ТПР соответствует направление, развиваемое школой
Э. Бёрна (автора книг «Игры, в которые играют люди», «Люди, которые
играют в игры»).
Чтобы сделать возможным математический анализ ситуации без учета
второстепенных факторов, строят упрощенную, схематизированную модель
ситуации, которая называется игрой, т.е. игра – это математическая модель
конфликтной ситуации.
Игра ведется по вполне определенным правилам, под которыми понимается
система условий, регламентирующая возможные варианты действий игроков;
объем информации каждой стороны о поведении другой; результат игры, к
которому приводит каждая данная совокупность ходов.
91
91.
Исторически сложилось так, что предметом математического анализа сначалабыли искусственные конфликтные ситуации, так называемые салонные игры
(шахматы, карточные игры и др.), поэтому терминология теории игр носит
несколько легкомысленный характер: стороны, участвующие в игре,
называются игроками (players), действия игроков называются ходами
(moves, actions), полезности исходов — выигрышами (payoff) и т.д.
Результат игры (выигрыш или проигрыш) вообще не всегда имеет
количественное выражение, но обычно можно, хотя бы условно, выразить его
числовым значением – средним выигрышем, полезностью и т.п.
Ход — выбор одного из предусмотренных правилами игры действий и его
осуществление. Ходы делятся на личные и случайные. Личным ходом
называется сознательный выбор игроком одного из возможных вариантов
действий и его осуществление. Случайным ходом называется выбор из ряда
возможностей, осуществляемый не решением игрока, а каким-либо механизмом
случайного выбора (бросание монеты, выбор карты из колоды и т. п.). Для
каждого случайного хода правила игры определяют распределение
вероятностей возможных исходов. Игра может состоять только из личных или
только из случайных ходов, или из их комбинации.
Стратегия (альтернатива) — это априори принятая игроком система решений
(вида «если-то»), которых он придерживается во время ведения игры, которая
может быть представлена в виде алгоритма и выполняться автоматически.
92
92.
Целью ТИ является выработка рекомендаций для разумного поведенияигроков в конфликтной ситуации, т.е. определение «оптимальной стратегии»
для каждого из них. Оптимальная стратегия – это стратегия, которая при
многократном повторении игры обеспечивает данному игроку максимальный
средний выигрыш.
Игры можно классифицировать:
1) по количеству игроков – игры 2 и n игроков;
2) по количеству стратегий – конечные и бесконечные (игра называется конечной,
если у каждого игрока имеется только конечное число стратегий, и бесконечной,
если хотя бы у одного из игроков имеется бесконечное число стратегий);
3) по характеру взаимодействия игроков – бескоалиционные (игроки не имеют
права вступать в соглашения, образовывать коалиции) и коалиционные
[кооперативные] (игроки могут вступать в коалиции).
В кооперативных играх коалиции заранее определены;
4) по характеру выигрышей – игры с постоянной суммой (общий капитал всех
игроков не меняется, а перераспределяется между игроками; сумма выигрышей
всех игроков равна нулю или константе) и игры с непостоянной суммой;
5) по виду функций выигрыша – матричные, биматричные, непрерывные, выпуклые
и др.;
6) по степени антагонизма игроков – игры со строгим соперничеством
(антагонистические) и игры с нестрогим соперничеством.
93
93.
Матричная игра — это конечная игра двух игроков с нулевой суммой, вкоторой задается выигрыш игрока I в виде матрицы (строка матрицы
соответствует применяемой стратегии игрока I, столбец — применяемой
стратегии игрока II, а на пересечении строки и столбца матрицы находится
выигрыш игрока I, соответствующий применяемым стратегиям).
Биматричная игра — это конечная игра двух игроков с ненулевой суммой,
в которой выигрыши каждого игрока задаются отдельными матрицами для
соответствующего игрока (в каждой матрице строка соответствует стратегии
игрока I, столбец — стратегии игрока II, на пересечении строки и столбца в
первой матрице находится выигрыш игрока II, во второй матрице — выигрыш
II игрока).
Непрерывной считается игра, в которой функция выигрышей каждого
игрока является непрерывной. Доказано, что игры этого класса имеют
решения, однако не разработано практически приемлемых методов их
нахождения.
Если функция выигрышей является выпуклой, то такая игра называется
выпуклой. Для них разработаны приемлемые методы решения, состоящие в
отыскании чистой оптимальной стратегии (определенного числа) для одного
игрока и вероятностей применения чистых оптимальных стратегий другого
игрока. Такая задача решается сравнительно легко.
94
94.
2. Нормальная форма матричной игрыПусть имеются два игрока — I и II. Будем считать, что каждый из игроков имеет
конечное множество альтернатив. В ТИ альтернативы (решения) принято
называть стратегиями.
Если игрок придерживается простой (несмешанной) альтернативы, то говорят,
что он следует чистой стратегии. Смешанной стратегией игрока
называется вектор, каждая из компонент которого показывает относительную
частоту использования игроком соответствующей чистой стратегии.
Пусть первый игрок имеет m (чистых) стратегий a1, . . . , am, второй — n
стратегий b1, . . . , bn. Такая игра называется игрой (m x n). Если первый игрок
использует стратегию ai, а второй bj, то игра закончится исходом Vij . В отличие
от игр против природы каждый исход имеет две полезности (выигрыша): с
точки зрения первого игрока uij = u(Vij) и с точки зрения второго игрока wij =
w(Vij).
Тогда игра двух лиц в нормальной форме означает, что определены:
G = (X, Y, M),
где X={a1, . . . , am} множество стратегий первого игрока, Y={b1, . . . , bn} множество стратегий второго игрока, M=M(a,b) платежная функция,
задаваемая в общем случае матрицей полезностей первого игрока U = ||uij||m×n
и матрицей полезностей второго игрока W = ||wij||m×n .
95
95.
Матрицей полезностей первого игрока96
96.
Степень антагонизма игроков определяется расхождением между ихматрицами полезностей. С этой точки зрения все игры можно разбить на два
класса: игры со строгим соперничеством (антагонистические) и игры с
нестрогим соперничеством.
В играх со строгим соперничеством uij wij A const , i, j , т. е. насколько
выгоден некоторый исход для первого игрока, настолько же он менее выгоден
для второго: игрок один стремится максимизировать свой выигрыш, а игрок 2 –
минимизировать свой проигрыш. Такие игры иначе называют играми с
постоянной суммой (constant sum games).
Очень часто рассматривают игры с нулевой суммой (zero-sum game):
uij wij 0, i, j
Определяя игру с нулевой суммой , нет необходимости задавать обе матрицы U
и W, достаточно одной из них, например U. Элементы этой матрицы можно
интерпретировать как величину выигрыша в единицах полезности первого
игрока у второго или, что то же самое, платежи второго игрока первому.
Поэтому U называется платежной матрицей (payoff matrix).
Доказано, что игру n лиц с ненулевой суммой всегда можно преобразовать в
игру n+1 лиц с нулевой суммой путем добавления «фиктивного» игрока.
В играх с нестрогим соперничеством интересы сторон не диаметрально
противоположны uij wij A const , i, j .
97
97.
Пример 1 (отгадывание монет).У каждого из игроков по две монетки: 1 руб. и 2 руб. Оба одновременно
выкладывают по одной из них на стол. Если достоинство монет совпадает,
то выложенные деньги забирает первый игрок, если нет — то второй.
Обозначим стратегии:
a1 — первый игрок выложил 1 руб.;
a2 — первый игрок выложил 2 руб.;
b1 — второй игрок выложил 1 руб.;
b2 — второй игрок выложил 2 руб.
Данная игра является простейшим примером игры со строгим
соперничеством и нулевой суммой и в общем случае ее необходимо было бы
описать двумя матрицами – матрицами выигрыша для каждого игрока:
U=
W=
b1 (1 руб.)
b2 (2 руб.)
a1 (1 руб.)
1
-1
a2 (2 руб.)
-2
2
b1
b2
a1
-1
1
a2
2
-2
98
98.
Но матричные игры удобнее описывать одной матрицей – в общемслучае (если это игра с ненулевой суммой):
b1
b2
a1
1; -1
-1; 1
a2
-2; 2
2; -2
или еще проще – матрицей выигрыша первого игрока, т.к. это игра
с нулевой суммой:
1/2
1/2
2/3
1/3
b1
b2
a1
1
-1
a2
-2
2
99
99.
Пример 2 («дилемма заключенного»).Двое подозреваемых A и B, находятся в разных камерах. Следователь,
навещая их поодиночке, предлагает сделку следующего содержания: если
один из них будет свидетельствовать против другого, а второй будет
молчать, то первый заключенный будет освобожден, а второго осудят на 10
лет. Если оба будут молчать, то отсидят по 1 году. Если оба предадут друг
друга, то каждый получит по 3 года. Каждый из заключенных должен
принять решение: предать подельника или молчать, не зная о том, какое
решение принял другой.
Данная игра является примером биматричной игры с нестрогим соперничеством
и ненулевой суммой.
Матрица выигрыша:
B (молчать)
B (предать)
А (молчать)
-1; -1
-10; 0
А (предать)
0; -10
-3; -3
Дилемма заключенного в экономике иллюстрирует ситуацию, когда решение ЛПР о
максимизации выигрыша может обернуться вредом для него самого или для другого
ЛПР. Дилемма также объясняет, почему продавцы зачастую стремятся к сговору на
рынке вместо конкуренции, которая была бы выгоднее для общества.
Диксит А., Нейлбафф Б. Теория игр. Искусство стратегического мышления в
бизнесе и жизни. – М.: Манн, Иванов и Фербер, 2015.
100
100.
3. Игры со строгим соперничеством: принципыпринятия решений
Принятие решения при противодействии существенно отличается от принятия
решения при неопределенности, вызванной незнанием состояния природы:
• в отличие от природы разумный игрок «изощрен и злонамерен», он
старается принять самые неблагоприятные для противника решения, при
этом оба игрока предполагаются одинаково разумными: любая идея,
которая может прийти в голову первому, может посетить и второго;
• обе стороны конфликта равноправны, оптимальное решение следует
рекомендовать каждому из игроков.
Эти обстоятельства диктуют следующие общие принципы принятия решений в
антагонистических играх:
• принцип осторожности;
• принцип уравновешенности.
101
101.
Принцип осторожности предписывает игрокам рассчитывать на самыйсильный вариант ответного хода противника, то есть игроки ориентируются
на гарантированный выигрыш. Стратегии, соответствующие этому принципу,
называются защитными.
Тогда в матричной игре защитная чистая стратегия первого игрока
выбирается по максиминному критерию (критерию максимина), при этом его
максимальный гарантированный выигрыш (т.е. не меньше ) равен нижней
цене игры:
max min uij
j
i
Защитная чистая стратегия второго игрока в матричной игре выбирается по
минимаксному критерию (критерию минимакса), при этом его (1-го игрока)
минимальный проигрыш (т.е. не больше ) равен верхней цене игры:
min max uij
j
i
В ТИ доказана теорема, утверждающая, что в антагонистической игре с
нулевой суммой максимин всегда не больше минимакса: .
Из самого определения защитных стратегий следует, что они существуют во
всех играх; более того, их может быть несколько. Отметим, что защитные
стратегии сами по себе не являются оптимальными решениями, если они не
сочетаются с принципом уравновешенности.
102
102.
Пример 3.Найдем защитные стратегии в игре Примера 1:
b1
b2
a1
1
-1
a2
-2
2
1
2
max
max min uij 1
i
min
j
-1
-2
min max uij 1
j
i
Следовательно, защитные стратегии в этой игре a = a1, b = b1,
и нижняя цена данной игры не совпадает с верхней.
103
103.
Пример 4.Найдем защитные стратегии в игре:
b1
b2
b3
min
a1
8
10
-5
-5
a2
15
17
-12
a3
16
18
-13
-12
-13
max
16
18
-5
max min uij 5
i
j
min max uij 5
j
i
Т.о., защитные стратегии a1, b3, причем в этой игре верхняя и нижняя
цены игры совпадают.
104
104.
3.1 Игры с седловой точкойСитуация, когда каждый из игроков, подозревая о том, что его противник
будет применять защитную стратегию, испытывает соблазн отойти от своей
защитной стратегии, называется неуравновешенностью защитных
стратегий.
Пара защитных стратегий матричной игры будет уравновешенной тогда,
когда нижняя и верхняя цена игры равны. Тогда если один из игроков
использует стратегию уравновешенной пары, то второму ничего не остается,
как также воспользоваться второй стратегией из этой пары, чтобы получить
наименьший гарантированный проигрыш.
Пара чистых стратегий ai∗, bj∗ уравновешена, если для любых i и j справедливо
неравенство:
uij* ui* j* ui* j
Число v ui j , которое представляет собой выигрыш первого
* *
игрока при использовании игроками оптимальных стратегий, называется
ценой (value) игры.
*
Игры с v
*
ui* j* называются играми с седловой точкой. 105
105.
Оптимальным решением игры в чистых стратегиях называетсяуравновешенная пара ai∗, bj∗ чистых стратегий. Уравновешенная пара
стратегий соответствует седловой точке (точкой равновесия или точкой
Нэша) платежной матрицы, т.е. такому ее элементу ui∗j∗ , который является
одновременно максимальным в своем столбце и минимальным в своей
строке. Поэтому проблема нахождения решения в чистых стратегиях
сводится к отысканию седловой точки платежной матрицы.
Необходимым и достаточным условием существования седловой точки (и,
соответственно, уравновешенной пары чистых стратегий ai∗, bj∗ ) является
равенство . В ТИ показано, что уравновешенная пара стратегий
всегда является защитной, однако защитная пара чистых стратегий является
уравновешенной только для игр с седловой точкой. В платежной матрице
может существовать несколько седловых точек, каждой из которых
соответствует уравновешенная (она же защитная) пара стратегий. В ТИ
показано, что никаких проблем при этом не возникает: допустима любая
комбинация оптимальных чистых стратегий, при этом все
они оказываются эквивалентными все седловые элементы равны.
Т.о., поиск оптимального решения в играх с седловой точкой заключается в
нахождении седловой точки и определении соответствующей ей
уравновешенной защитной пары стратегий, т.е. имеет место решение в
чистых стратегиях. Эта пара стратегий и составляет оптимальное решение.
Если нет седловой точки, то оптимальное решение в смешанных стратегиях.
106
106.
Пример 4.Найдем защитные стратегии в игре:
b1
b2
b3
min
a1
8
10
-5
-5
a2
15
17
-12
a3
16
18
-13
-12
-13
max
16
18
-5
max min uij 5
i
j
min max uij 5
j
i
Т.о., защитные стратегии a1, b3, причем в этой игре верхняя и нижняя
цены игры совпадают.
107
107.
Итак, в каждой игре с седловой точкой:1) если обе стороны придерживаются своих оптимальных чистых стратегий,
то средний выигрыш равен чистой цене игры, одновременно
являющейся ее нижней и верхней ценой;
2) если же одна из сторон придерживается своей оптимальной чистой
стратегии, а другая отклоняется от своей оптимальной чистой
стратегии, то от этого отклоняющаяся сторона может только проиграть и
ни в коем случае не может увеличить свой выигрыш.
Игры, имеющие седловую точку, называют вполне определенными, или
играми с полной информацией (игроки равносильны, знают чистые
стратегии друг друга, знают предшествующие ходы противника).
В ТИ показано, что в антагонистической игре 2-х лиц с нулевой суммой,
заданной платёжной матрицей U uij , для которой выполняется условие
uij ui , j 1 имеется хотя бы одна седловая точка.
108
108.
3.2 Игры без седловой точкиСуществуют игры, не имеющие уравновешенных пар чистых стратегий.
Для таких игр возникла идея использования смешанных
(рандомизированных) стратегий.
Выбирая смешанную стратегию, игроки фиксируют распределения частоты
(интенсивностей, а при рандомизации вероятностей) на множестве своих
чистых стратегий. Таким образом, смешанная стратегия первого игрока это
набор чисел
m
X p1 ,..., pm , pi 0,
p 1
i
i 1
а смешанная стратегия второго игрока набор чисел
Y q1 ,..., qn , q j 0,
n
q 1
j 1
j
Концепция рандомизированной смешанной стратегии занимает важное место в
теории игр: на ней строится вся теория антагонистических игр без седловой
точки, но эта концепция далеко не бесспорна. Если игрок собирается играть в
данную игру всего раз в жизни, и исходы в ней весьма ответственны на
карту могут быть поставлены благополучие и даже жизнь человека, то он
предпочтет использовать защитную чистую стратегию, обеспечивающую ему
наибольший гарантированный выигрыш.
109
109.
В случае когда игра ведется много раз и выигрыш накапливается, тоабстрактный средний выигрыш приобретает практический смысл: если число
партий достаточно велико, то к нему в силу закона больших чисел стремится
среднее арифметическое выигрыша в последовательности партий.
Если игрок I выбирает смешанную стратегию X, а игрок II – чистую bj , то
средний выигрыш первого игрока
M X , b j uij pi
m
i 1
Если игрок I выбирает чистую ai, а игрок II – смешанную стратегию Y, то
средний выигрыш первого игрока
n
M ai , Y uij q j
j 1
Если оба игрока выбирают смешанные стратегии X и Y, то средний выигрыш
первого игрока
m
n
m n
M X , Y pi M ai , Y q j M X , b j piuij q j
i 1
j 1
i 1 j 1
Основная теорема ТИ (теорема фон Неймана): Каждая конечная
*
антагонистическая игра двух лиц с нулевой суммой имеет цену v ,
и у каждого игрока имеется, по крайней мере, одна оптимальная
*
*
стратегия (возможно, в области смешанных стратегий X ,Y ).
В играх без седловой точки для цены игры всегда справедливы
неравенства: v* .
110



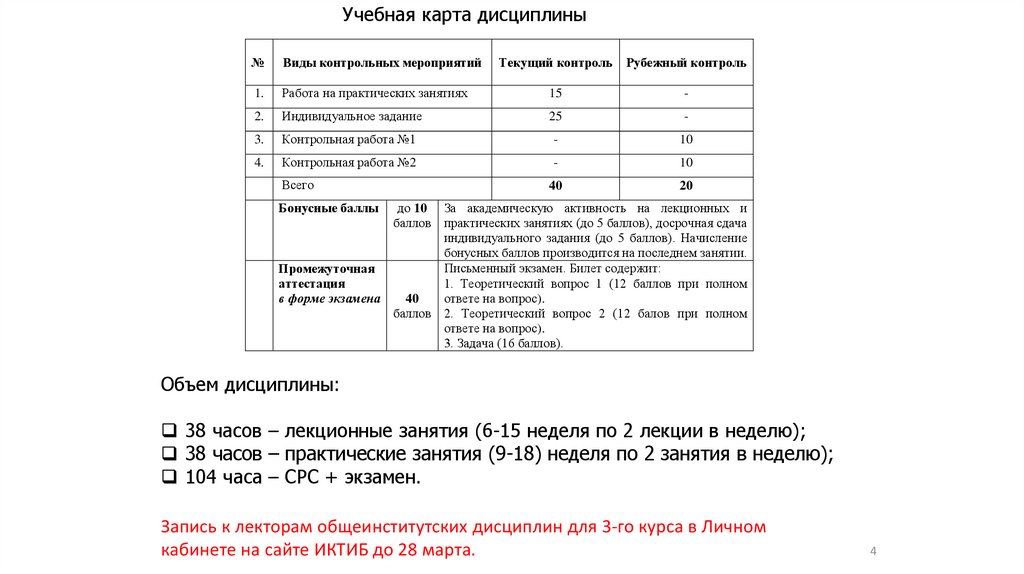























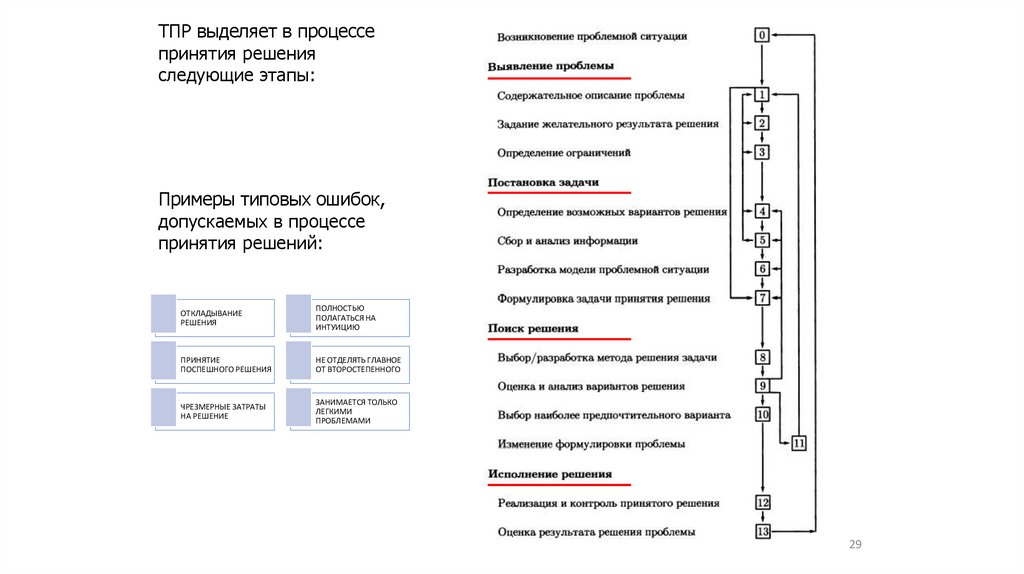

































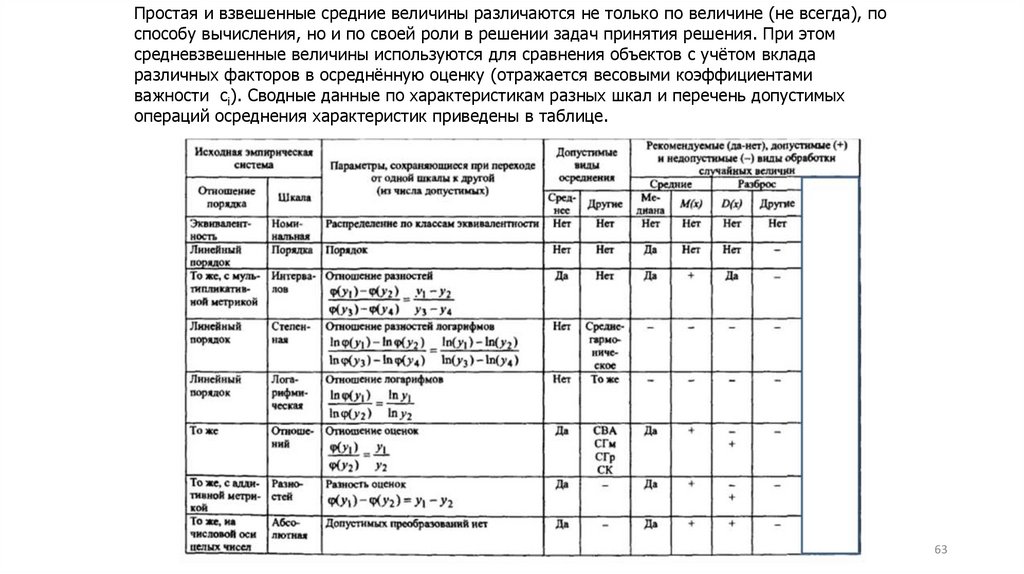
















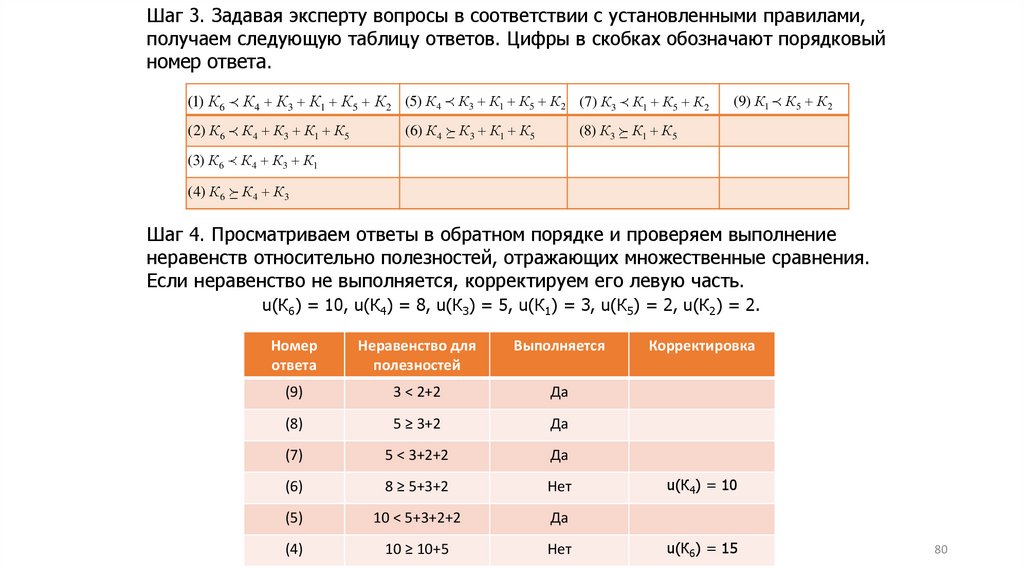
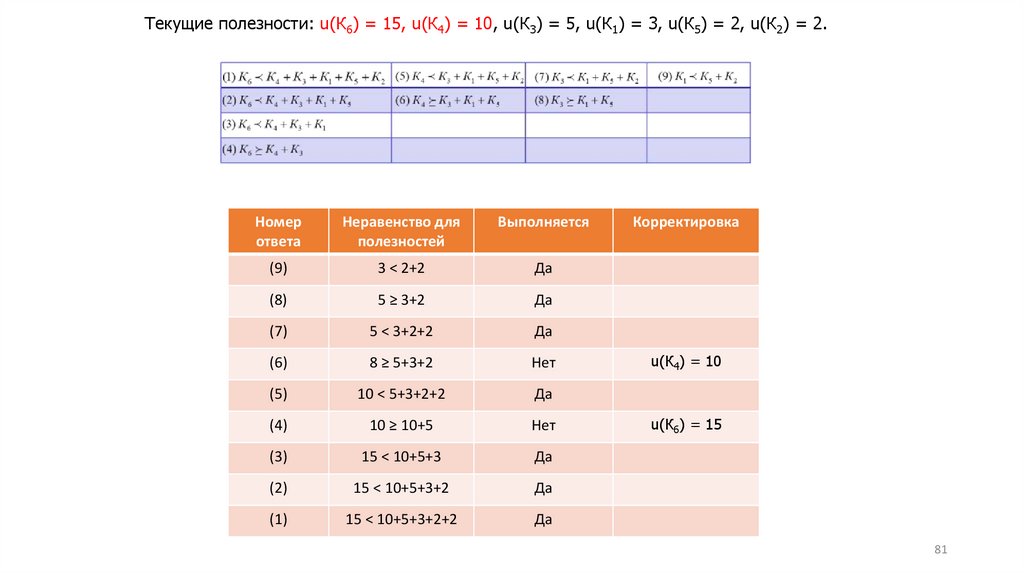




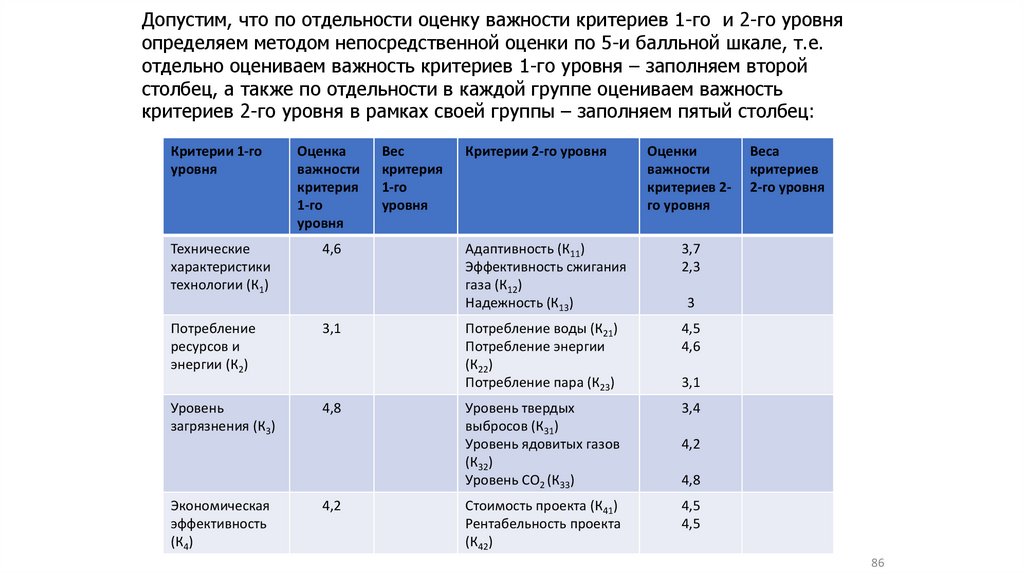











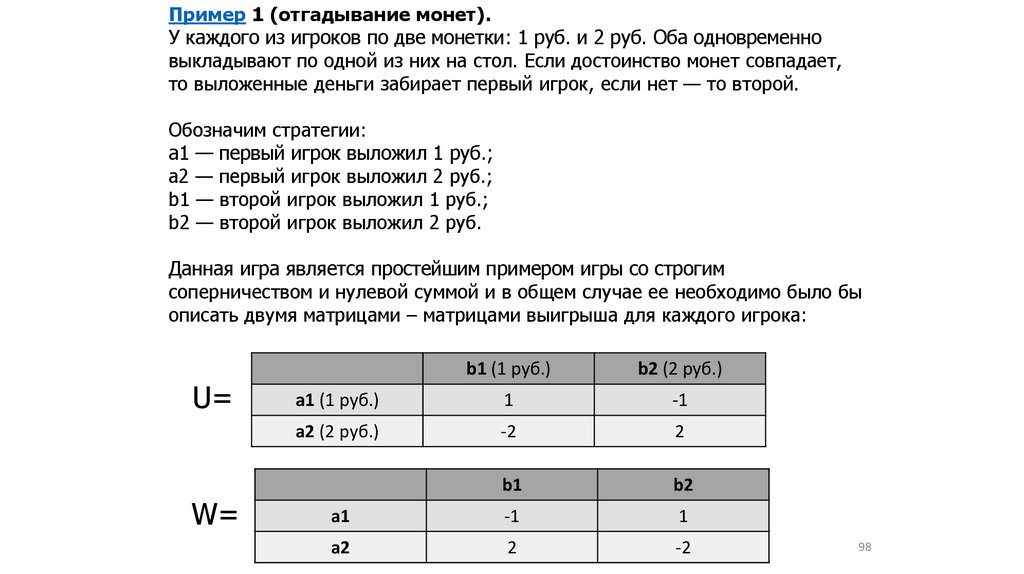

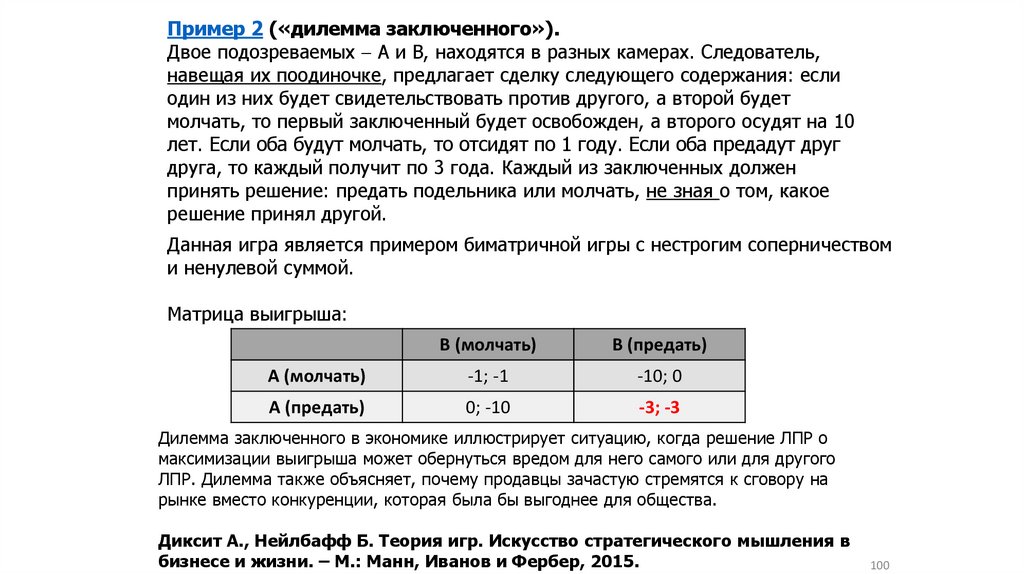











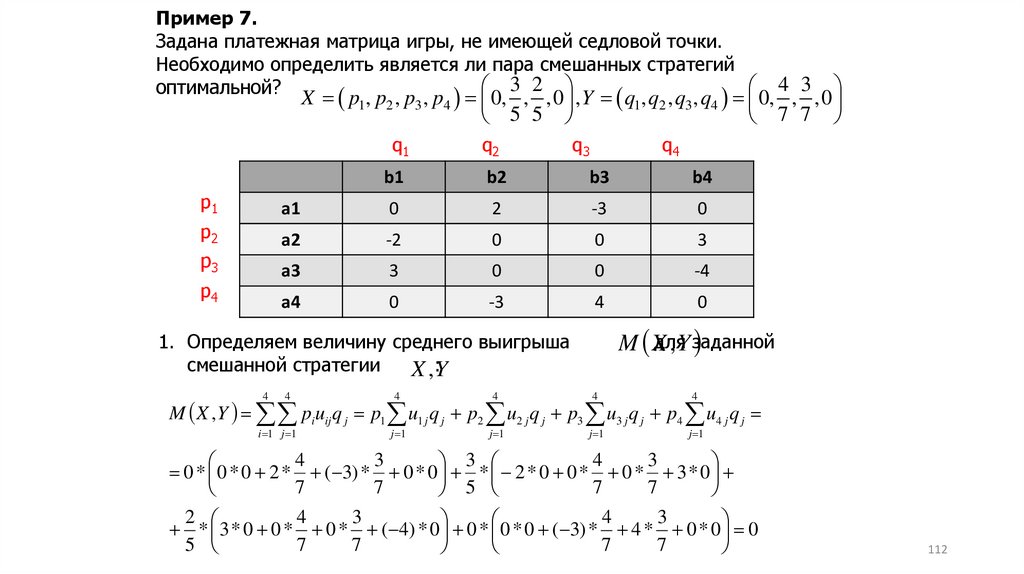


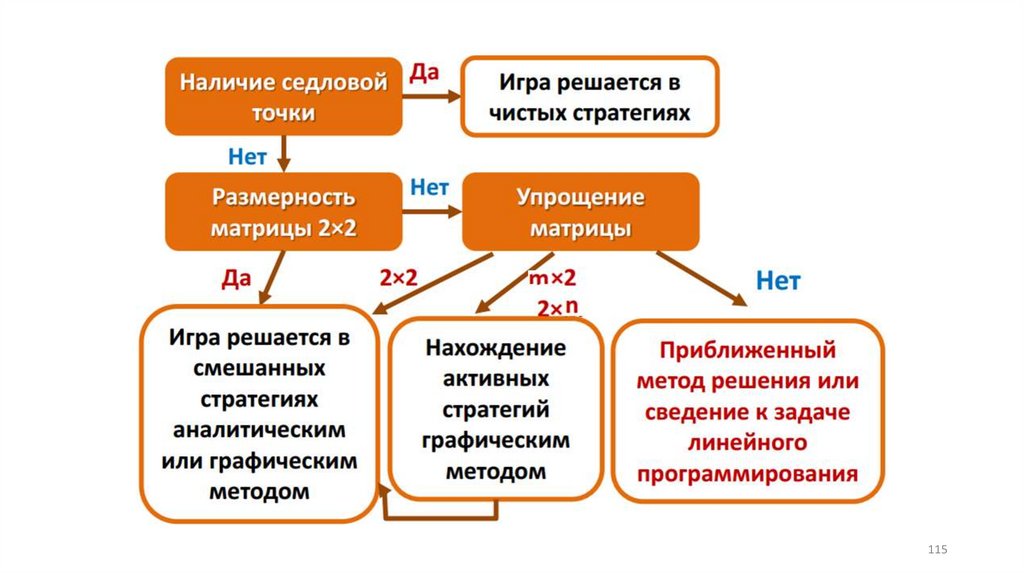



















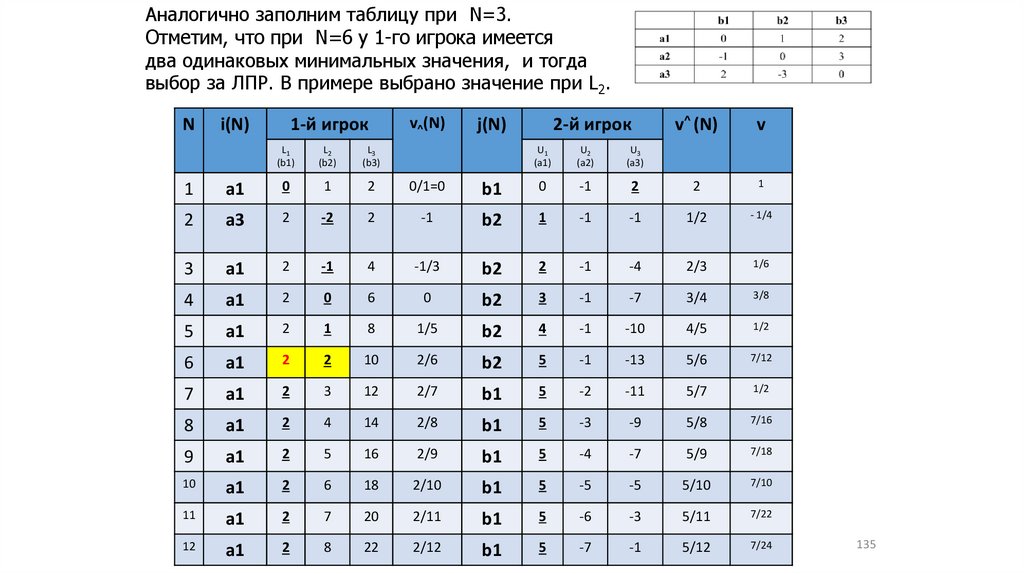









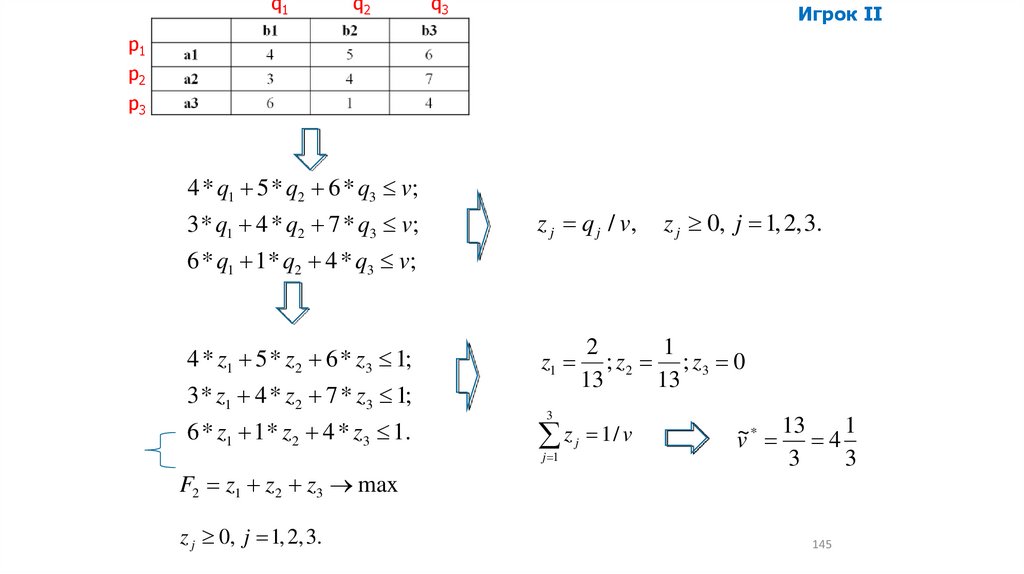



























































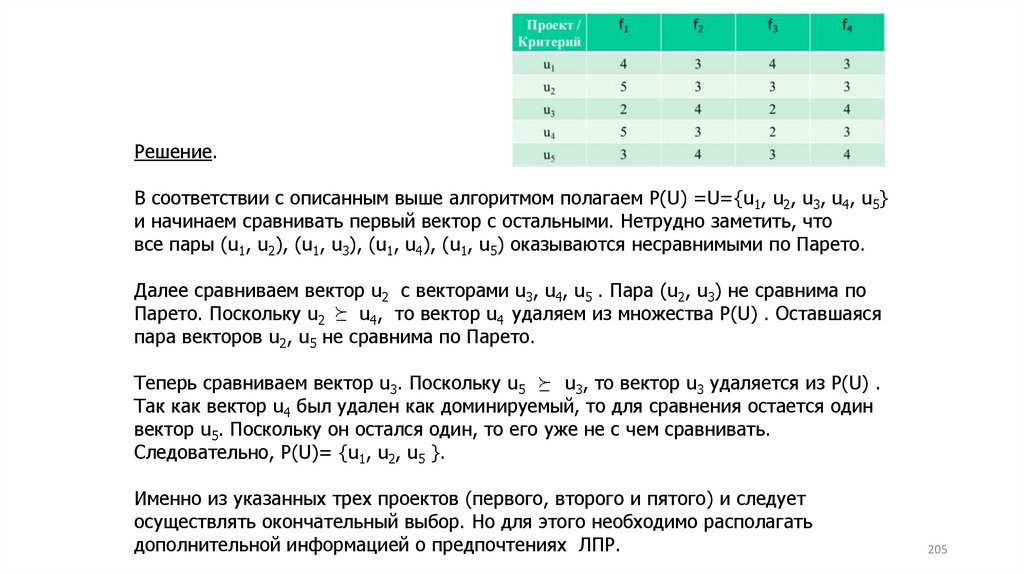






















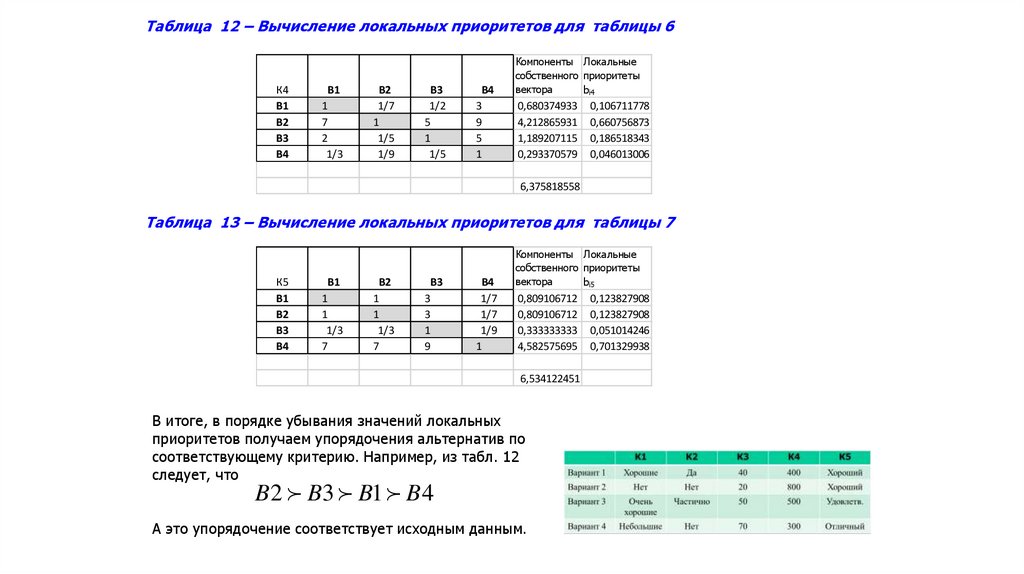


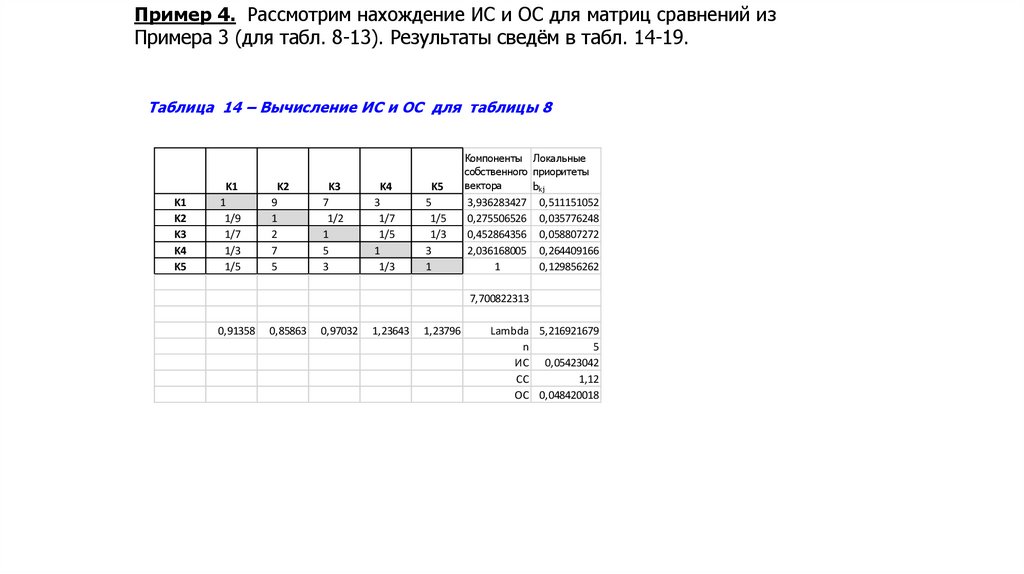

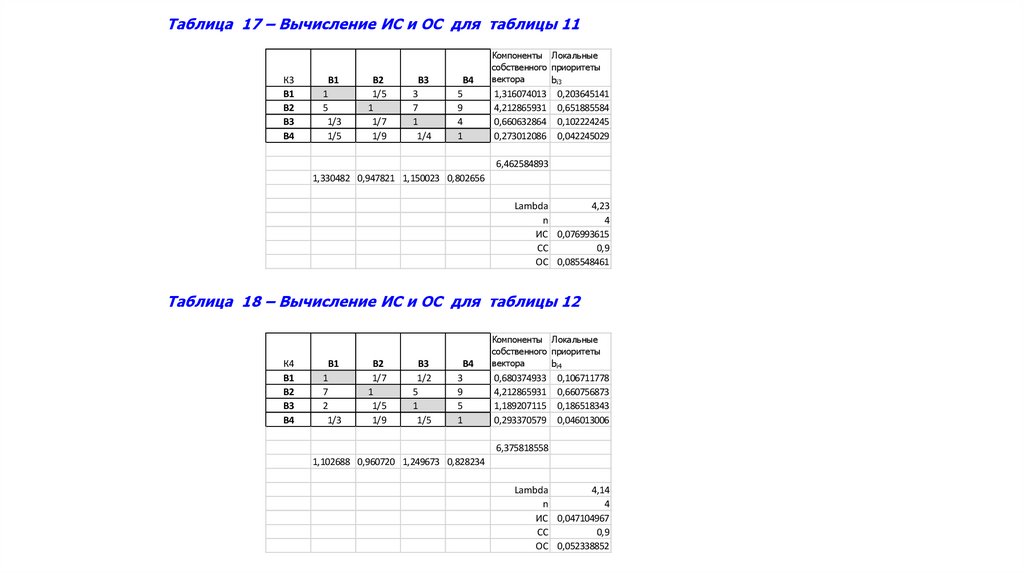





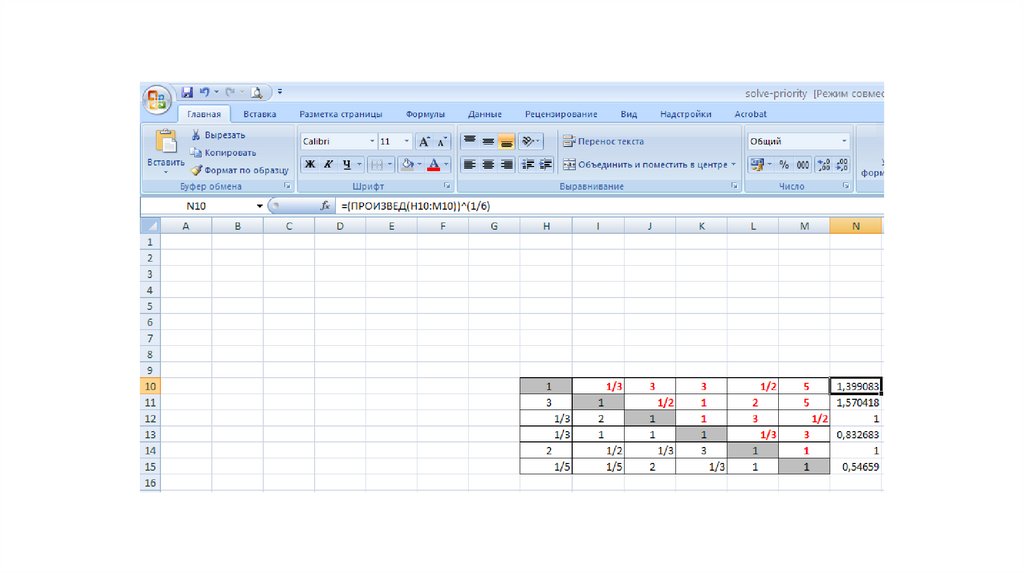







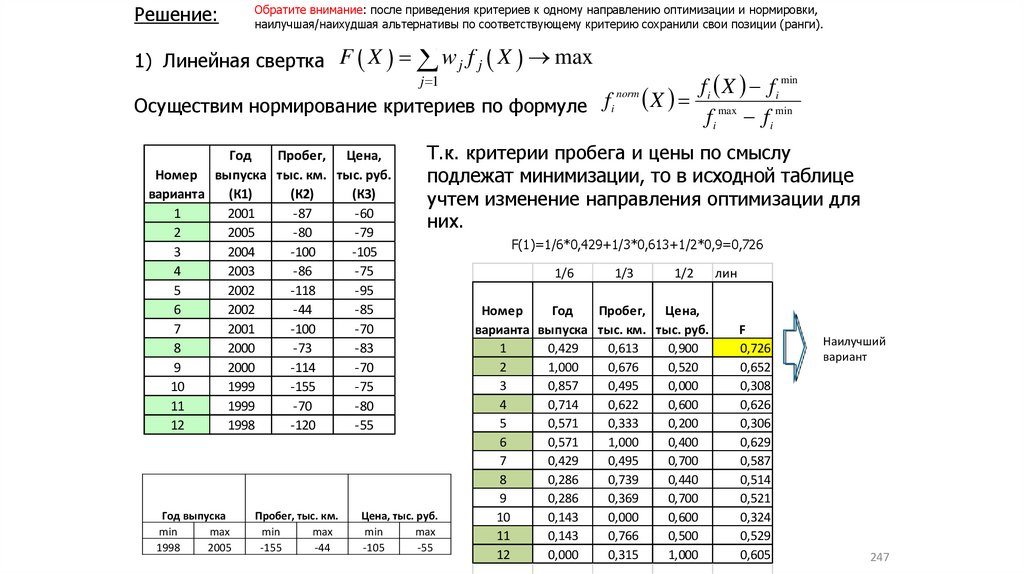





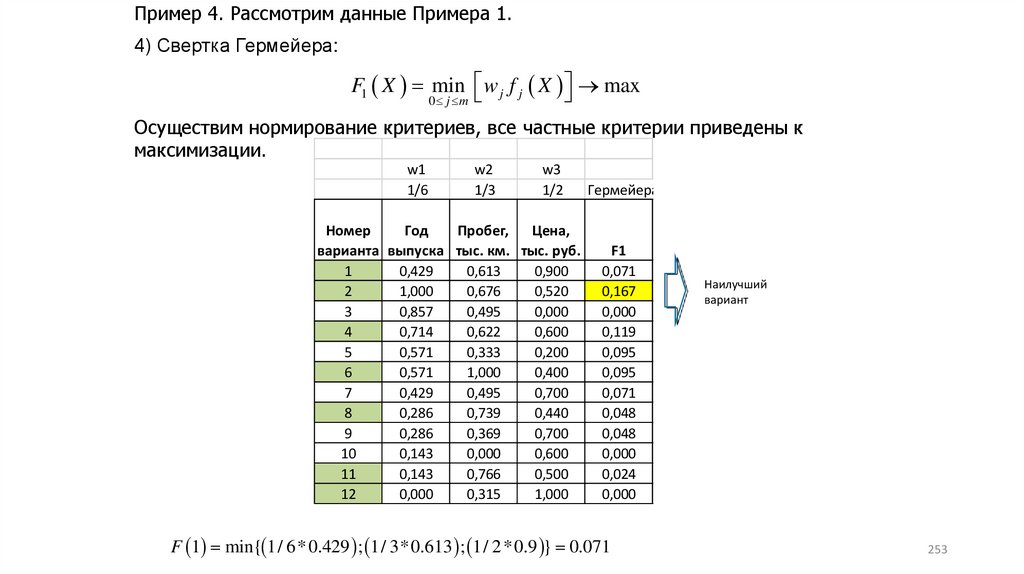






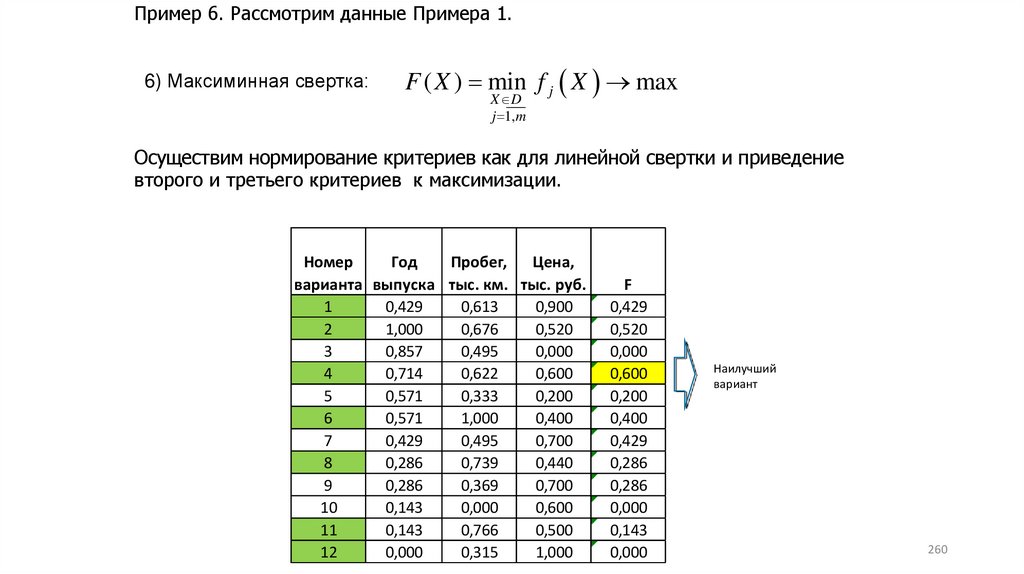

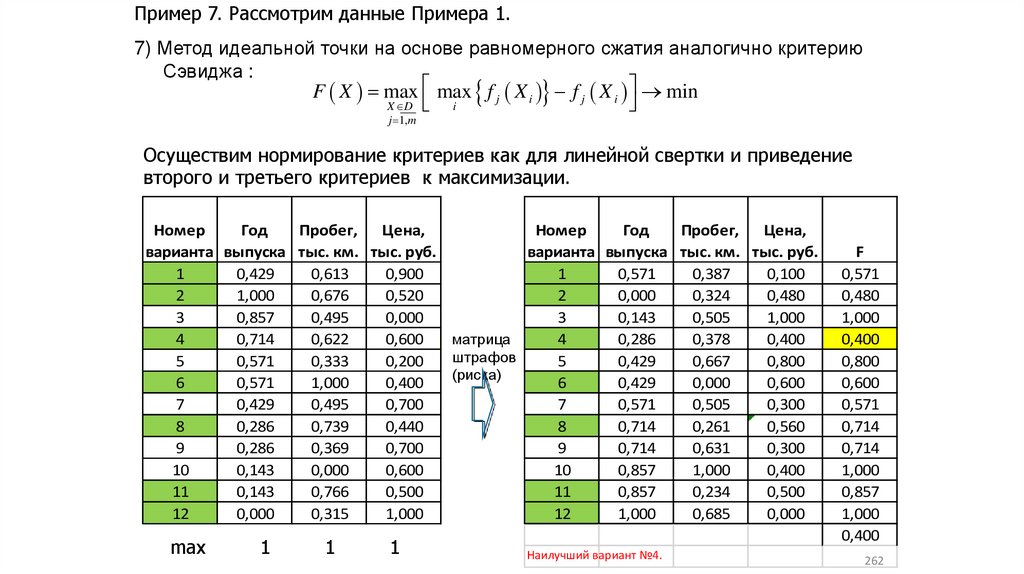

































































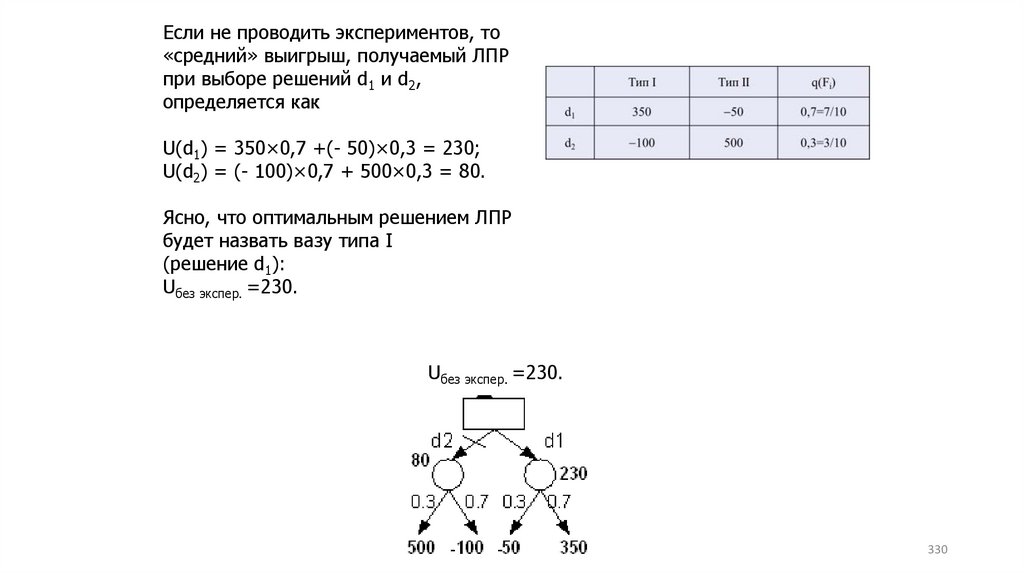




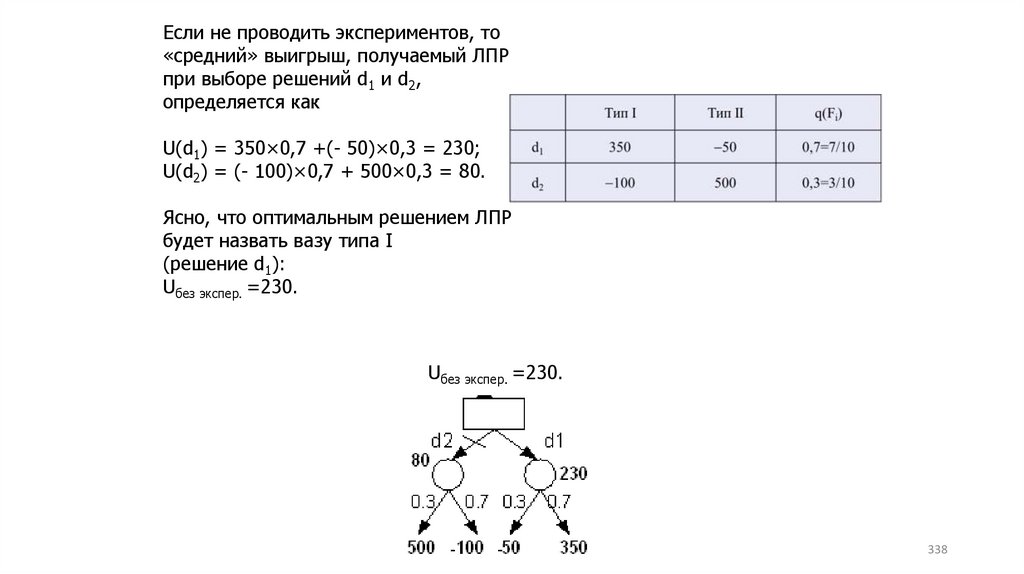


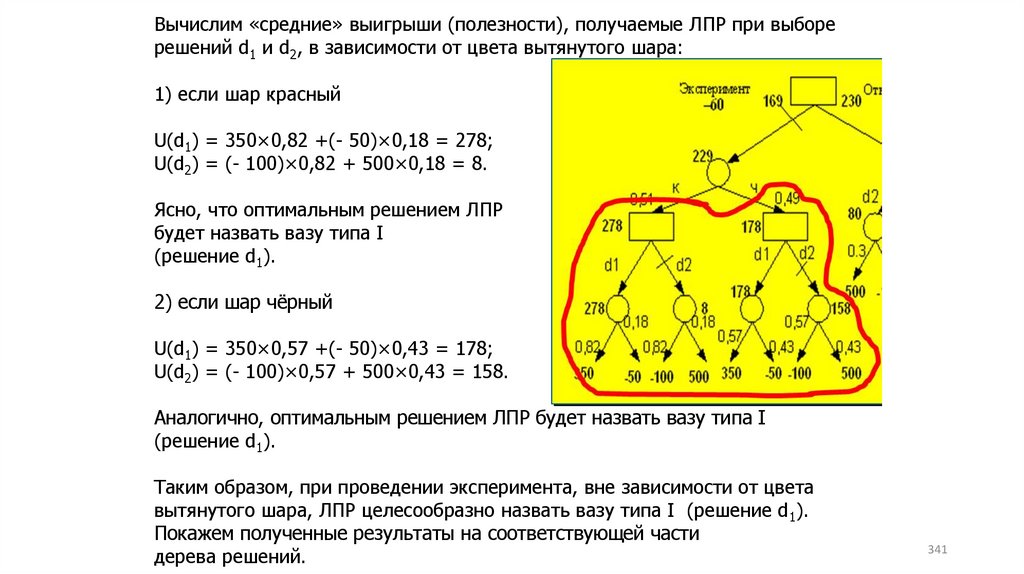


















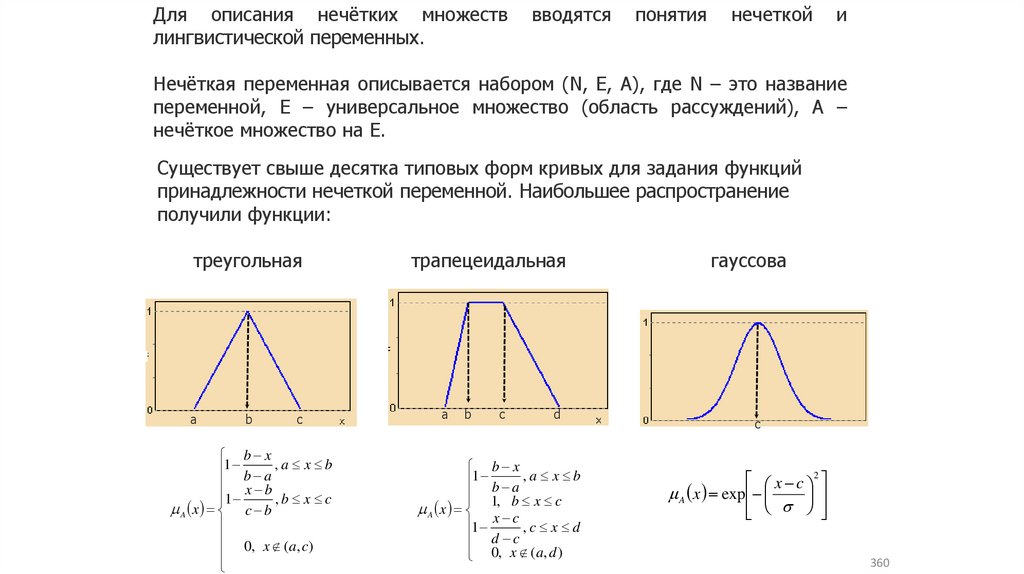





































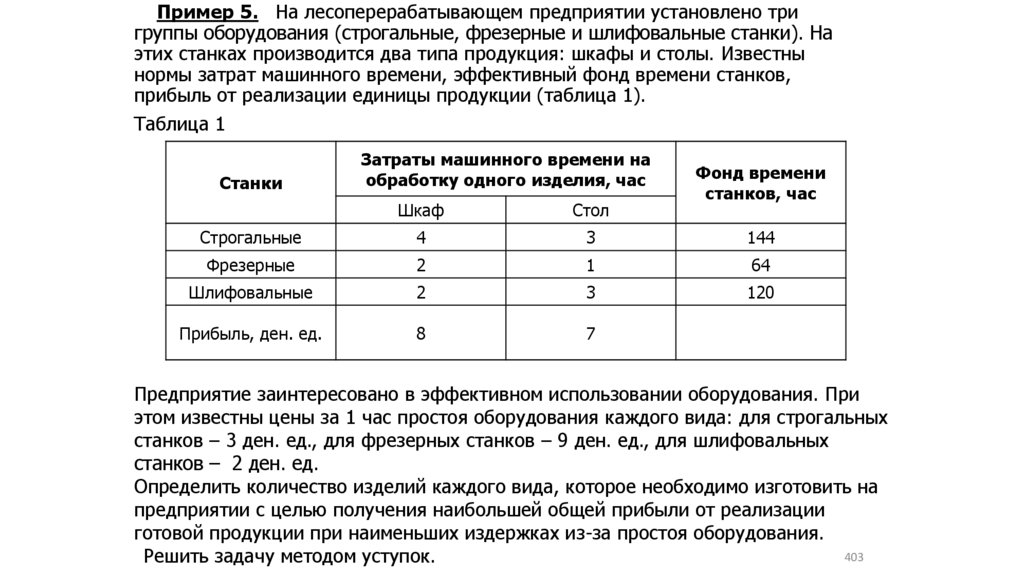




































































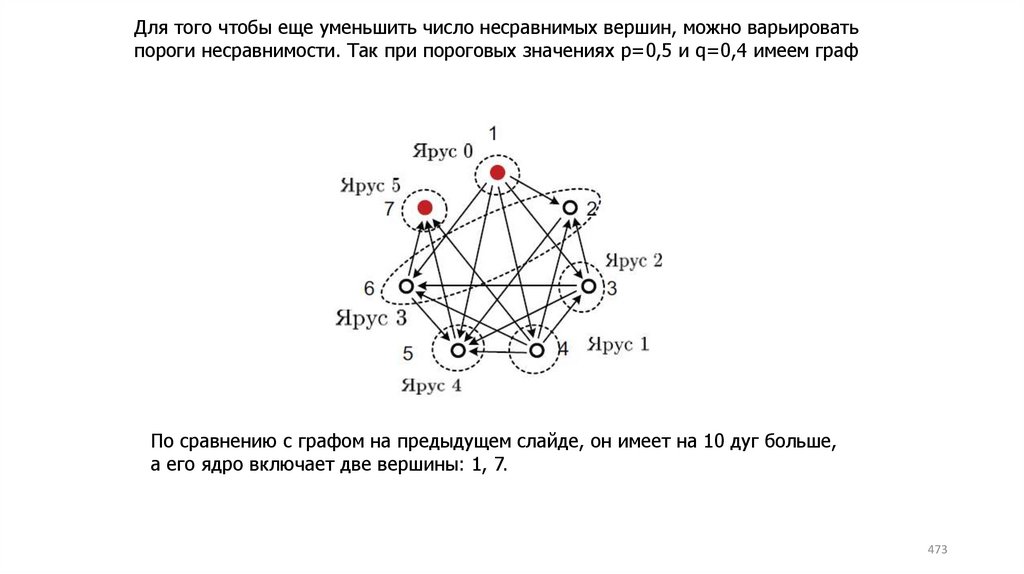




















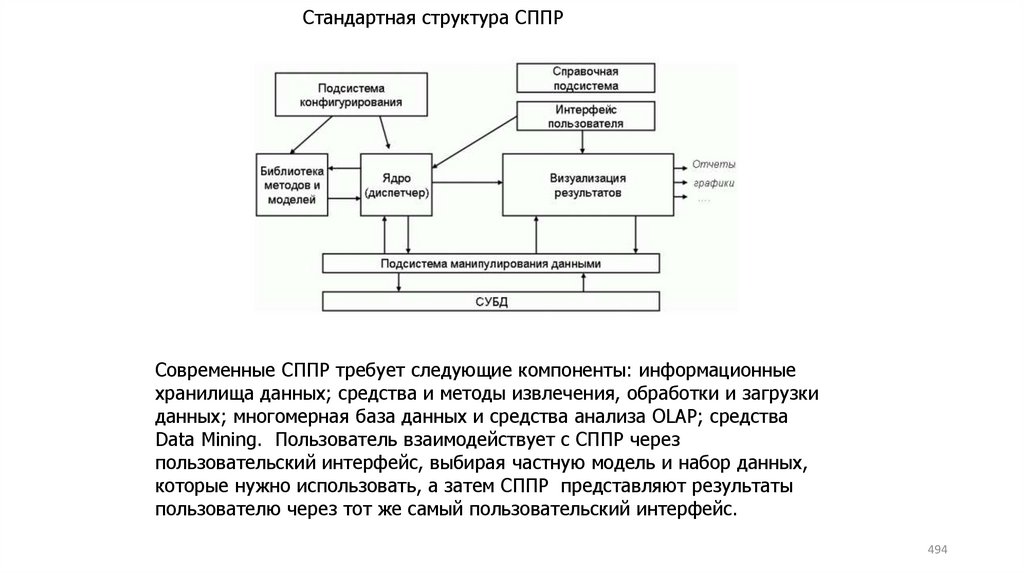







 Менеджмент
Менеджмент








