Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками

1.

Введение декартовых
координат в пространстве.
Формулы середины отрезка и
расстояния между двумя точками.

2.

Вспомним, как определяется координатная(числовая) прямая.
1) Изображаем произвольную прямую;
2) Придаем ей положительное направление и обозначаем её;
3) Выбираем произвольную точку за начало отсчета;
4) Определяем длину единичного отрезка (масштаб).
М
0
1
х
а
Тогда любой точки этой координатной прямой соответствует единственное
действительное число a. И наоборот, любое действительное число может быть
изображено единственной соответствующей точкой, для которой это число
является координатой. Записывают: M(a).

3.

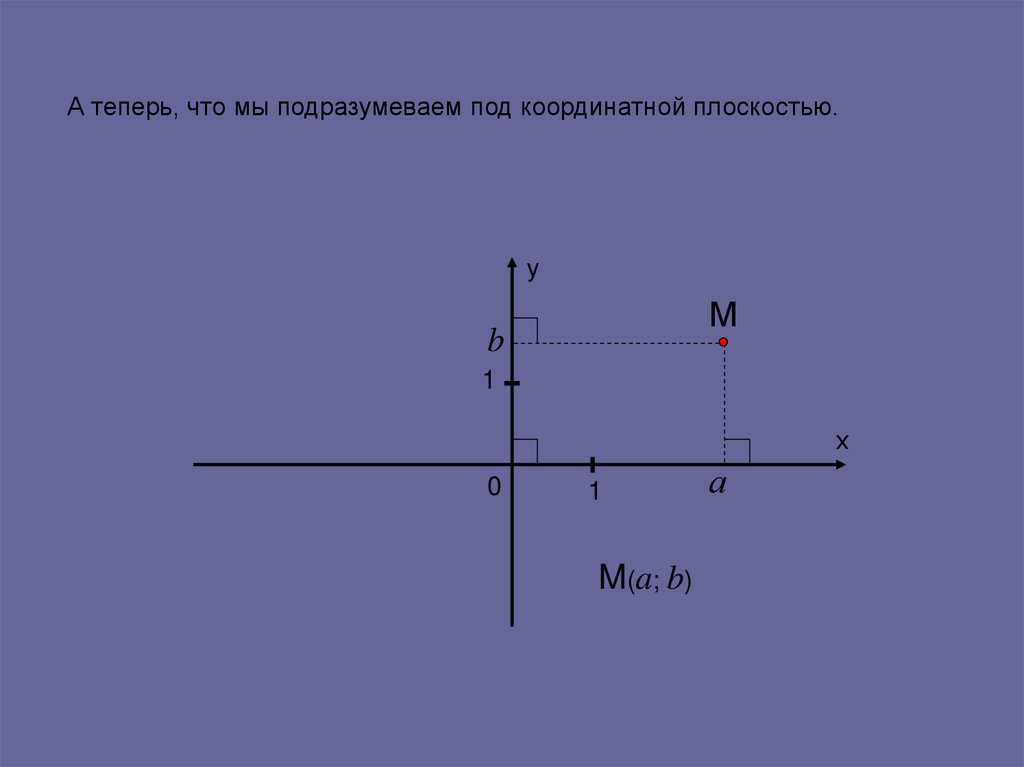
А теперь, что мы подразумеваем под координатной плоскостью.
у
М
b
1
х
0
1
M(a; b)
а

4.

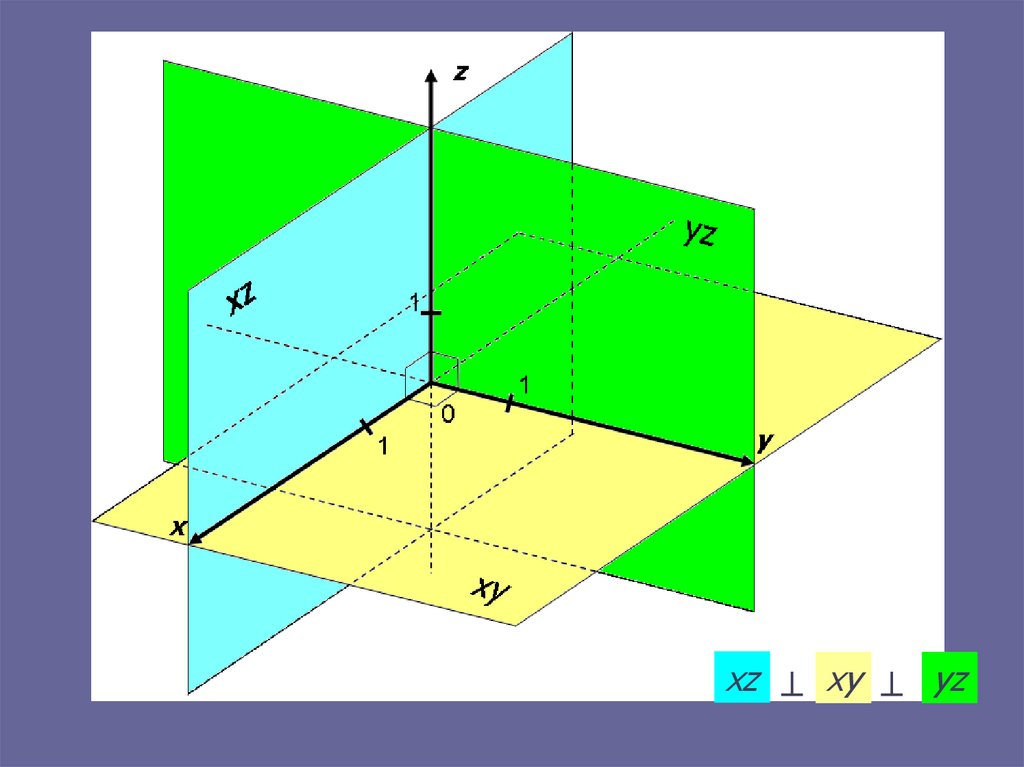
Выберем в пространстве три
попарно перпендикулярные
координатные прямые x, y, z,
пересекающиеся в одной
точке 0, соответствующей
началу координат каждой оси.
z
Ox Oy Oz
Пунктиром показаны
отрицательные части
осей.
1
1
0
1
y
x
Координатные оси:
Ox – ось абсцисс
Oy – ось ординат
Oz – ось аппликат

5.

z
1
1
0
1
y
x
Координатные плоскости:
Oxz
Oxy
Oyz

6.

Координатные плоскости:
xz xy yz

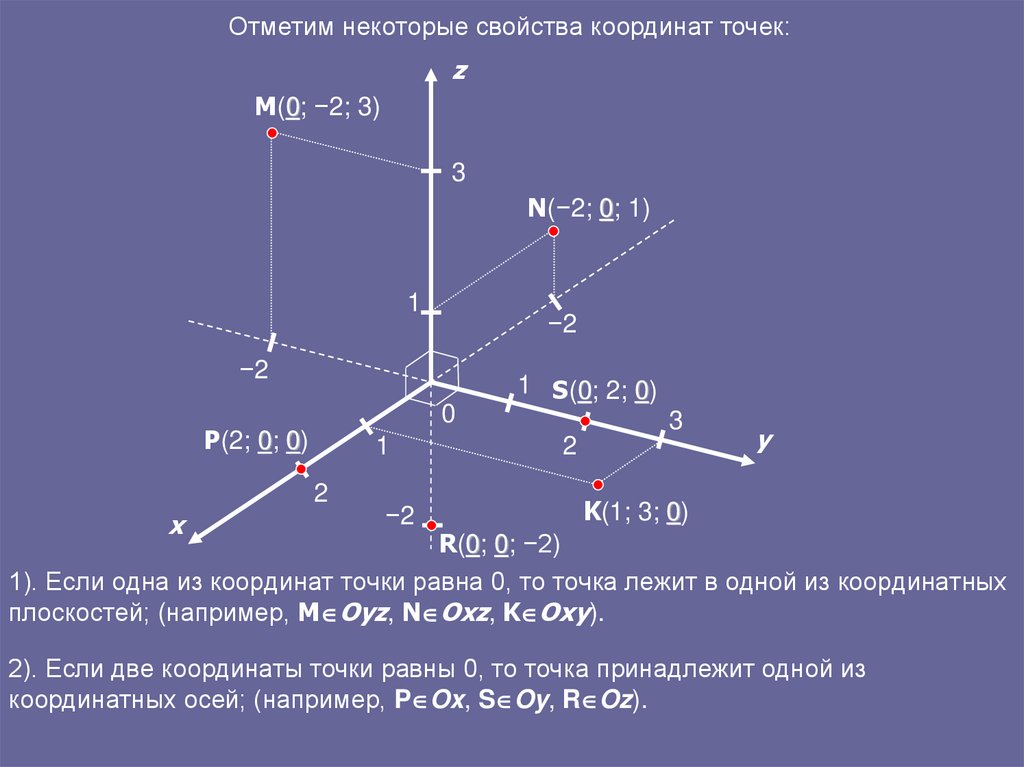
7. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например, MOyz, NOxz, KOxy).

Отметим некоторые свойства координат точек:
z
M(0; −2; 3)
3
N(−2; 0; 1)
1
−2
−2
1 S(0; 2; 0)
0
P(2; 0; 0)
1
2
x
−2
3
2
y
K(1; 3; 0)
R(0; 0; −2)
1). Если одна из координат точки равна 0, то точка лежит в одной из координатных
плоскостей; (например, M Oyz, N Oxz, K Oxy).
2). Если две координаты точки равны 0, то точка принадлежит одной из
координатных осей; (например, P Ox, S Oy, R Oz).

8. Формулы середины отрезка и расстояния между точками на плоскости.

x1 x2 y1 y2
М
;
2
2
АВ
x2 x1 y2 y1
2
2

9. Задача №1. Найдите координаты середины отрезка АВ и длину отрезка АВ, если:

1 вариант А (3;-1), В (-2;4)
2 вариант А (3;4), В (2; -1)

10. о

I вариант
о
Дано: А (3;-1), В (-2;4),
точка М – середина АВ.
Найти: IАВI, М(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ
2 3 2 4 ( 1) 2
25 25
50 5 2
II вариант
Дано: А (3;4), В (2;-1),
точка С – середина АВ.
Найти: IАВI, С(x;y).
Решение:
АВ
x2 x1 2 y2 y1 2
АВ (2 3) 2 ( 1 4) 2 1 25 26
x x2 y1 y 2
М 1
;
2
2
x x2 y1 y 2
С 1
;
2
2
3 ( 2) 1 4
М
;
2
2
3 2 4 ( 1)
С
;
2
2
М 0,5;1,5
Ответ:
АВ 5 2
М 0,5;1,5
С 2,5;1,5
Ответ: АВ
26
С 2,5;1,5

11.

Расстояние между точками A(x1; y1; z1) и B(x2; y2; z2)
АВ
x2 x1 y2 y1 z2 z1
2
2
2
Координаты середины отрезка АВ, где A(x1; y1; z1) и B(x2; y2; z2)
x1 x2 y1 y2 z1 z2
M
;
;
2
2
2

12. Задача № 2.

Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты
середины отрезка АВ и
его длину.