Похожие презентации:
Декартовы координаты в пространстве. Формулы середины отрезка и расстояния между двумя точками
1.
Тема: «Декартовы координаты впространстве.
Формулы середины отрезка и
расстояния между двумя точками»
2.
-Вы уже знакомы с прямоугольной(Декартовой) системой координат на
плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт
3.
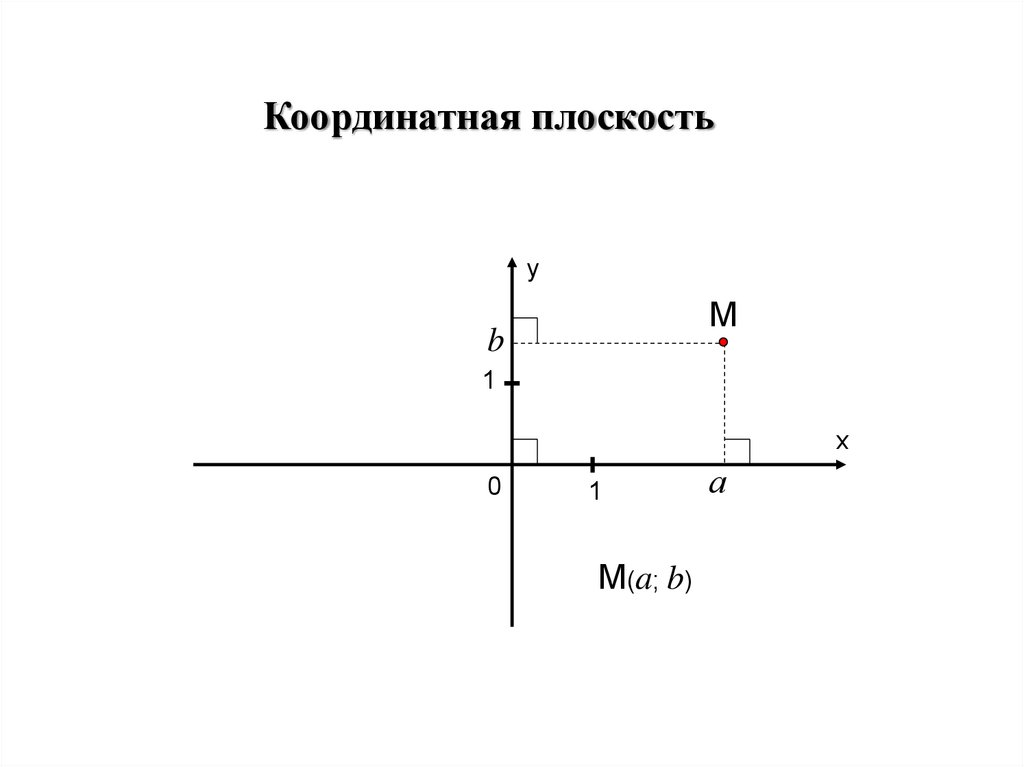
Координатная плоскостьу
М
b
1
х
0
1
M(a; b)
а
4.
-Прямоугольную системукоординат в пространстве ввёл
швейцарский математик
Леонард Эйлер
в XVIIIв.
5.
Выберем в пространстве трипопарно перпендикулярные
координатные прямые x, y, z,
пересекающиеся в одной
точке 0, соответствующей
началу координат каждой оси.
z
Ox Oy Oz
Пунктиром показаны
отрицательные части
осей.
1
1
0
1
y
x
Координатные оси:
Ox – ось абсцисс
Oy – ось ординат
Oz – ось аппликат
6.
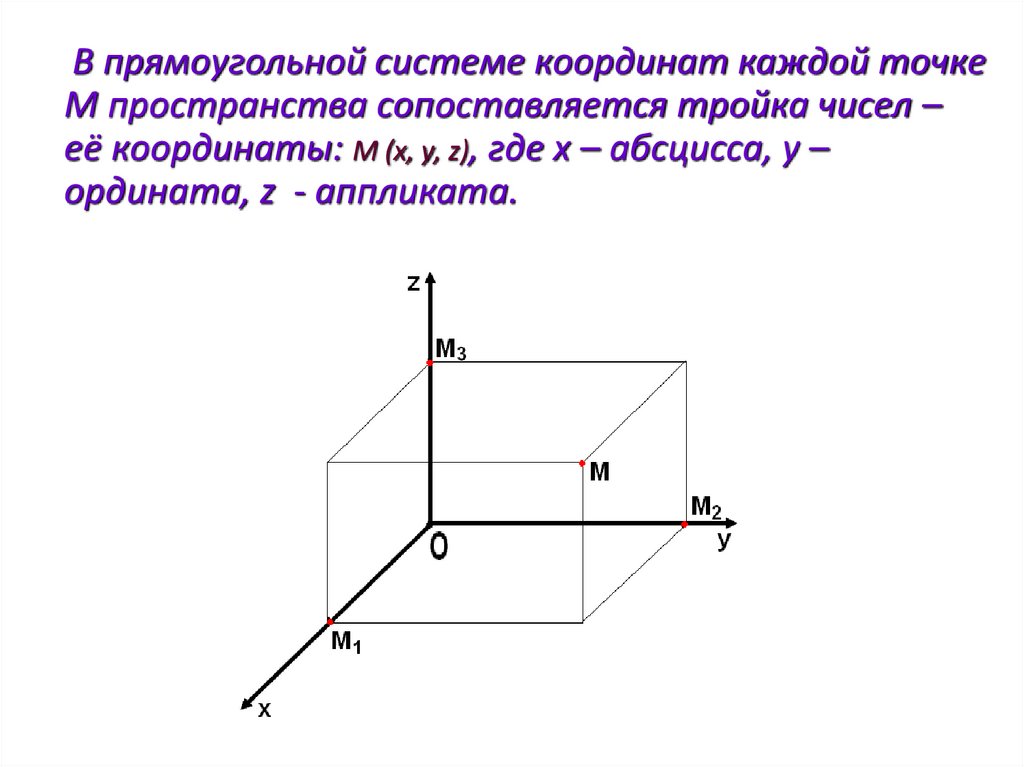
В прямоугольной системе координат каждой точкеМ пространства сопоставляется тройка чисел –
её координаты: М (х, у, z), где х – абсцисса, у –
ордината, z - аппликата.
7. Построение точек в прямоугольной системе координат
1.А(3;6;5) На оси Ох- отметить 3
единичных отрезка и провести
прямую через эту точку, причем
параллельную оси Оу
2.
На оси Оу отметить два единичных
отрезка и провести прямую через эту
точку, причем параллельную оси Ох
3.
Через точку пересечения двух прямых
провести прямую параллельную оси
Оz, и отметить на ней 5 единичных
отрезков вверх.
z
А
0
х
3
6
у
8. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например, MOyz, NOxz, KOxy).
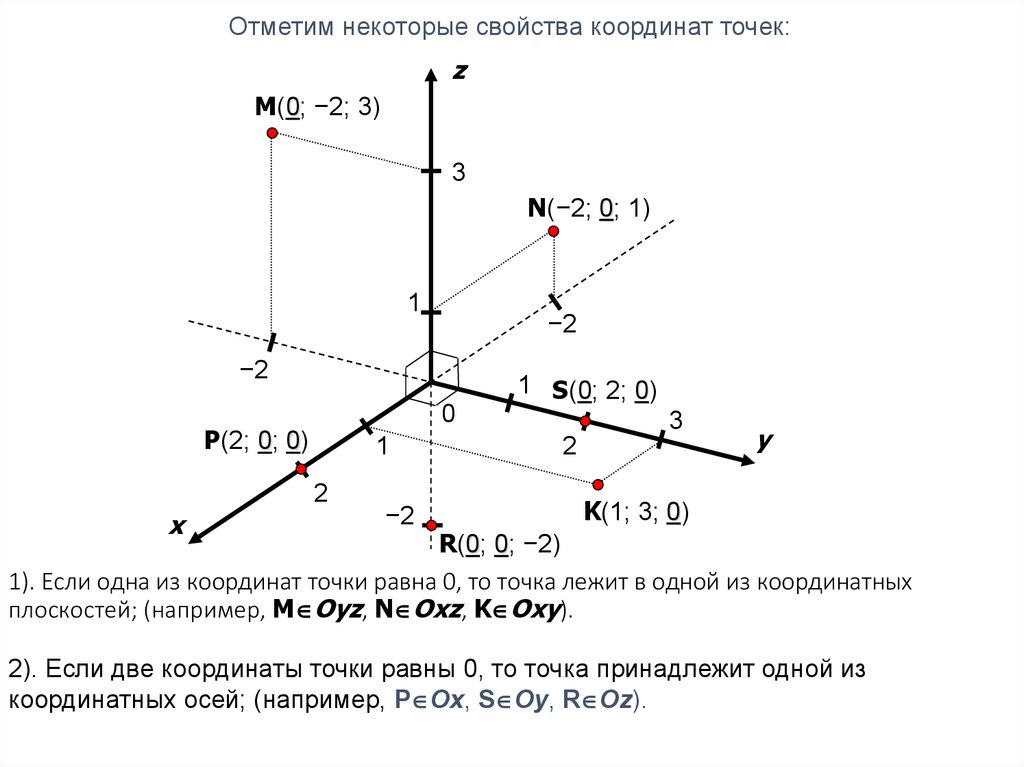
Отметим некоторые свойства координат точек:z
M(0; −2; 3)
3
N(−2; 0; 1)
1
−2
−2
1 S(0; 2; 0)
0
P(2; 0; 0)
1
2
x
−2
3
2
y
K(1; 3; 0)
R(0; 0; −2)
1). Если одна из координат точки равна 0, то точка лежит в одной из координатных
плоскостей; (например, M Oyz, N Oxz, K Oxy).
2). Если две координаты точки равны 0, то точка принадлежит одной из
координатных осей; (например, P Ox, S Oy, R Oz).
9.
Точка лежитв координатной
на оси
плоскости
Ох
Оу
Оz
Oxy
Oyz
Oхz
(х,0,0)
(0,у,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)
10.
zI
I
I
A(-1; 3;-6)
I
I
I
С
I
I
I
I
В
Найдите координаты
точек А, В, С
I
B(-2;-3; 4)
I
O
I
I
I
I
I
I
x
I
I
I
I
I
I
I
А
I
y
C( 3;-2; 6)
11.
Даны точки:А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
D (-4; -1; 0)
Е (0; -3; 0)
F (1; 2; 3)
Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz.
Назовите точки, лежащие
в плоскости Охz.
В (0; 0; -7)
Назовите точки, лежащие
в плоскости Оху.
С (2; 0; 0)
Е (0; -3; 0)
12. Выполнение задания с последующей проверкой.
Начертить прямоугольную трехмернуюсистему координат и отметить в ней
точки:
А (1; 4; 3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)
13. Проверка.
zС
А
(1;
4;
3)
В
D
С (0;
(0;
(4; 5;
0;
0; -3)
3)
4)
А
D
1
1
1
y
В
x
14. Определите координаты точек:.
zА
А (3; 5; 6)
В (0; -2; -1)
D
С (0; 6; 0)
D (-3; -1; 0)
С
1
1
В
x
1
y
15. Формулы середины отрезка и расстояния между точками в пространстве.
x1 x2 y1 y2 z1 z 2М
;
;
2
2
2
АВ
x2 x1 y2 y1 z2 z1
2
2
2
16. Задача № 1:
Дано: А (1;-1;2), В (3;1;-2)Постройте точки в
координатном пространстве.
Найдите координаты середины
отрезка АВ и его длину.
17. Решение задач
№2.№3.
18. Укажите пары равных векторов
№4. Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)Определить: пары равных векторов
Решение:
Равны соответствующие координаты у
Равны соответствующие координаты у
векторов
,
значит, они
векторов
,
, значит, они
попарно равны
попарно равны
19. Выполнить задание:
• Даны векторы:а 3;5; 7
c 0;1;8
b 4; 1;3
d 3;0;0
• Найти вектор равный:
а) 2 а
6;10; 14
б) 3 b
в) a b
7;4; 4
г) b с
4; 2; 5
д) а b d
10;4; 4
12;3; 9
e) 3d 2c
9; 2; 8
20.
№5.№1.
Д/З.
№6.
№2.
Д/З.
21.
№7.22.
Д/з. Найти скалярное произведение векторов:1)
a {1; 10; 7} b {0; 7; 0}
2)
a {7; 25; 0} b {11; 0; 54}
23. Самостоятельная работа №1
1-вариант2-вариант
№1.
№1.
Отметьте точки в прямоугольной Отметьте точки в прямоугольной
системе координат в
системе координат в
пространстве:
пространстве:
A(2;2;4), В(-3;-4;-5), С(-1;2;-3),
A(3;3;5), В(-4;-3;-5), С(-4;2;3),
О(0;2;3), К(0;0;4).
О(1;-3;0), К(0;5;0).
№2.
№2.
Найдите координаты середины
Найдите координаты середины
отрезка АВ и длину отрезка АВ, отрезка АВ и длину отрезка АВ,
если:
если:
а) А (3;-1), В (-2;4);
а) А (3;4), В (2;-1);
б) А(3;4;-6), В(-5;-3;-8).
б) А(-6;2;-3), В(-4;-6;-9).
24. Самостоятельная работа №2
1-вариант2-вариант
№2. Определите коллинеарные ли векторы





















 Математика
Математика








