Задача о сильном точечном взрыве

1.

Задача о сильном
точечном взрыве

2.

БОМБАРДА МАКСИМА
2

3.

Решение задачи о
распространении
сферической ударной
волны большой
мощности, возникшей
в результате сильного
взрыва: Л. И. Седов
(1946) и Дж. фон
Нейман (1947)
Леонид Иванович Седов
(1907-1999)
Кто первый решил узнать, что
происходит и выжить!?
Джон фон Нейман
3
(1903-1957)

4.

Основные уравнения
задачи о сильном взрыве:
Уравнение Эйлера:
→ → p
v
(v )v
t
Уравнение непрерывности:
→
div( v ) 0
t
ds s →
v s 0
dt t Условие адиабатичности среды
4

5.

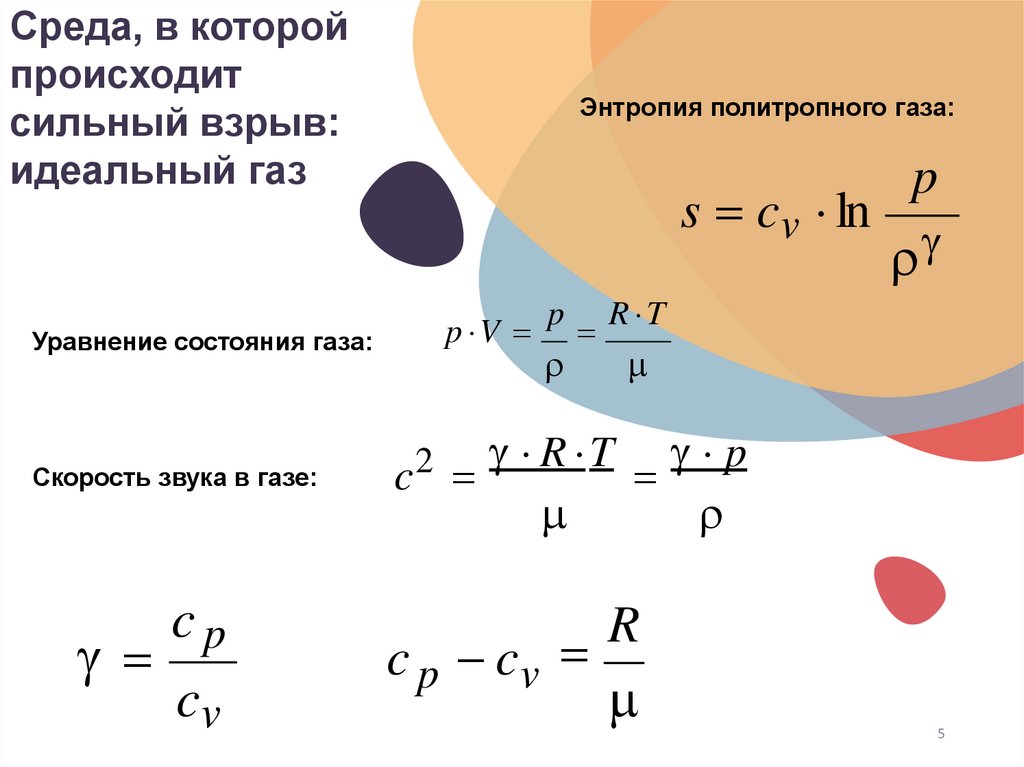
Среда, в которой
происходит
сильный взрыв:
идеальный газ
Уравнение состояния газа:
Скорость звука в газе:
cp
cv
Энтропия политропного газа:
s cv ln
p V
p
p
R T
R T p
2
c
c p cv
R
5

6.

Уравнения
центральносимметричного
адиабатического
движения
идеального газа:
v
v
1 p
v
t
r
r
2
1 (r v)
0
t r 2
r
v ln p 0
t
r
6

7.

Процедура построения
автомодельного решения
1
p1
Условие большой интенсивности ударной волны:
В этом случае движение газа определяется двумя параметрами:
E
1
— энергия, выделившаяся при
взрыве:
2
2
[E] M L T
— начальная плотность газа:
[ 1 ] M L 3
Анализ размерностей даѐт:
[E] 1 [ 1 ] 2 [T ] 3 [L] 1 1 2 1 3 2
5
5
7
5

8.

1
2
E 5
R(t) ( ) t 5
1
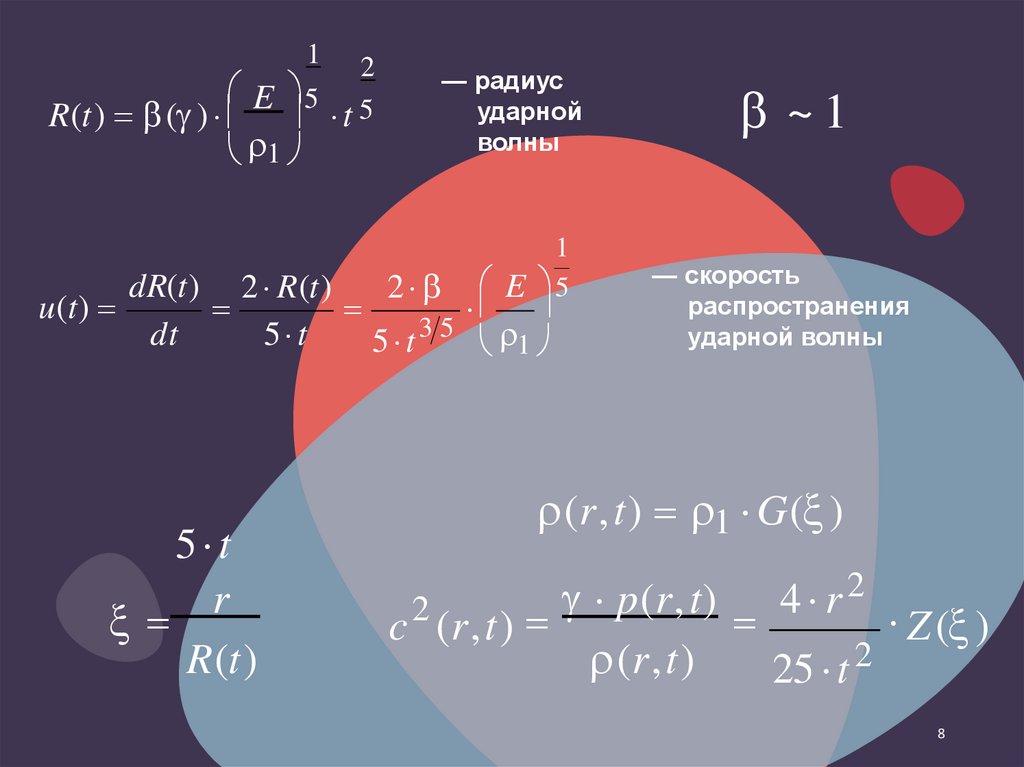
— радиус
ударной
волны
1
E 5
dR(t) 2 R(t)
2
u(t)
dt
5 t
5 t 3 5 1
5 t
r
R(t)
~1
— скорость
распространения
ударной волны
(r,t) 1 G( )
2
p(r,
t)
4
r
2
Z ( )
c (r,t)
(r,t)
25 t 2
8

9.

Уравнения в частных
производных свелись к
системе
обыкновенных
дифференциальных уравнений
(ОДУ):
d ln G d ln Z (1 V ) dV
V (5 2 V )
2
2 Z
d ln d ln
Z
d ln
dV
d ln G
(1 V )
3 V
d ln
d ln
d ln Z
d ln G
5 2 V
( 1)
1 V
d ln
d ln
9

10.

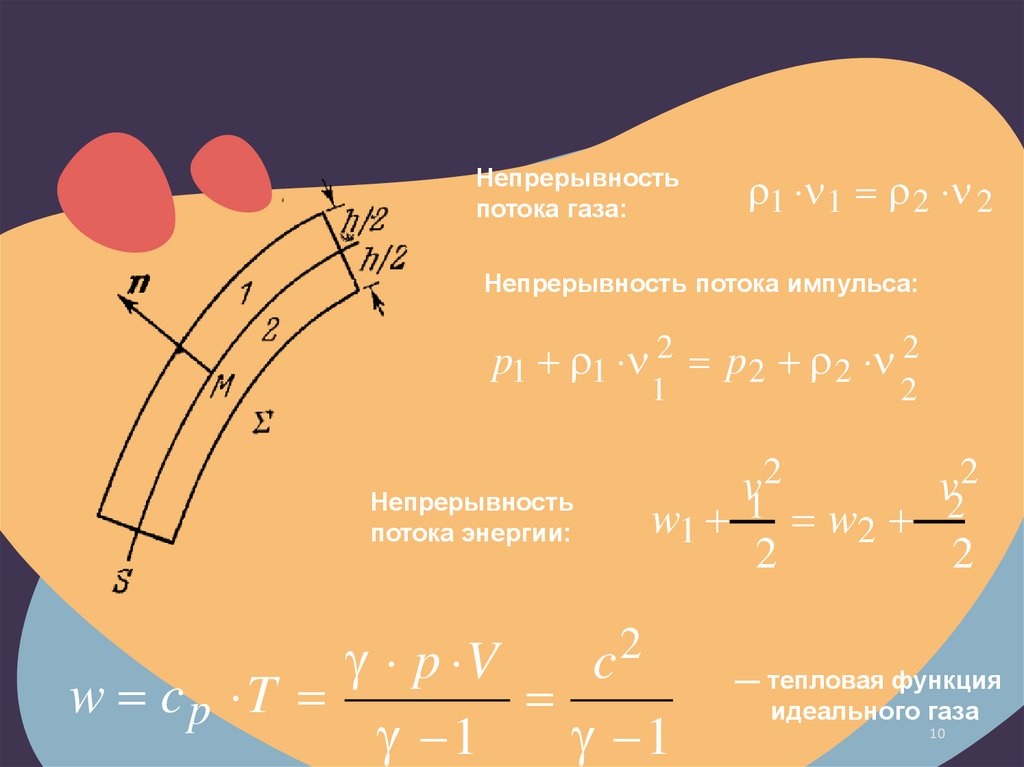
Непрерывность
потока газа:
1 1 2 2
Непрерывность потока импульса:
p1 1 2 p 2 2 2
1
Непрерывность
потока энергии:
w1
p V
w c p T
1
1
2
c
2
v12
2
w2
v22
2
— тепловая функция
идеального газа
10

11.

Граничные условия к системе ОДУ:
2
v2
u(t)
1
1
2 1
1
2
p2
1 u 2 (t)
1
Граничные условия
являются начальными
условиями во времени
2
V (1)
1
1
G(1)
1
2 ( 1)
Z (1)
2
( 1)
ln
[0, )

12.

Результаты численных расчѐтов
решения системы ОДУ для
воздуха (γ=1,4):

13.

Полная энергия системы
сохраняется:
R(t)
v2
4 r 2 dr
E
2
0
— следствие пренебрежения
давлением p1 невозмущѐнного
газа
2
c
p V
cv T
1 ( 1)
— внутренняя энергия
политропного газа
V 2
4
Z
G
d 1
2
(
1)
0
1
5
16
25
Для воздуха β=1,033
Your Date Here
Your Footer Here

14.

Поведение физических
величин
вблизи эпицентра
сильного взрыва
1
5
V ~ 2
0
Z ~ 5 2
G ~ 5 3 2
v
~
v2
p
const
p2
2
3
~ 1
T
T2

15.

Цилиндрическая и плоская
симметрия сильного взрыва
v
v
1 p
v
t
r
r
1 (r d 1 v)
0
t r d 1
r
v ln p 0
r
t
→ d
r R
d 1,2,3
15

16.

Системы ОДУ для задач о сильном взрыве с
тремя вышеописанными типами симметрии
принадлежат к классу систем Морса-Смейла
Стивен
Смейл
(р. 1930)
Марстон
Морс
(1892-1977)
Ольга
Починка
Елена Гуревич

17.

Эволюция фрактальных
неоднородностей
1
→(1) →
v (r ,0) ( f (r), 0, 0)
Усечѐнная функция Вейерштрасса:
f (r)
N
a n cos( b n r r0 )
n 1
17

18.

Your Date Here
Your Footer Here
18

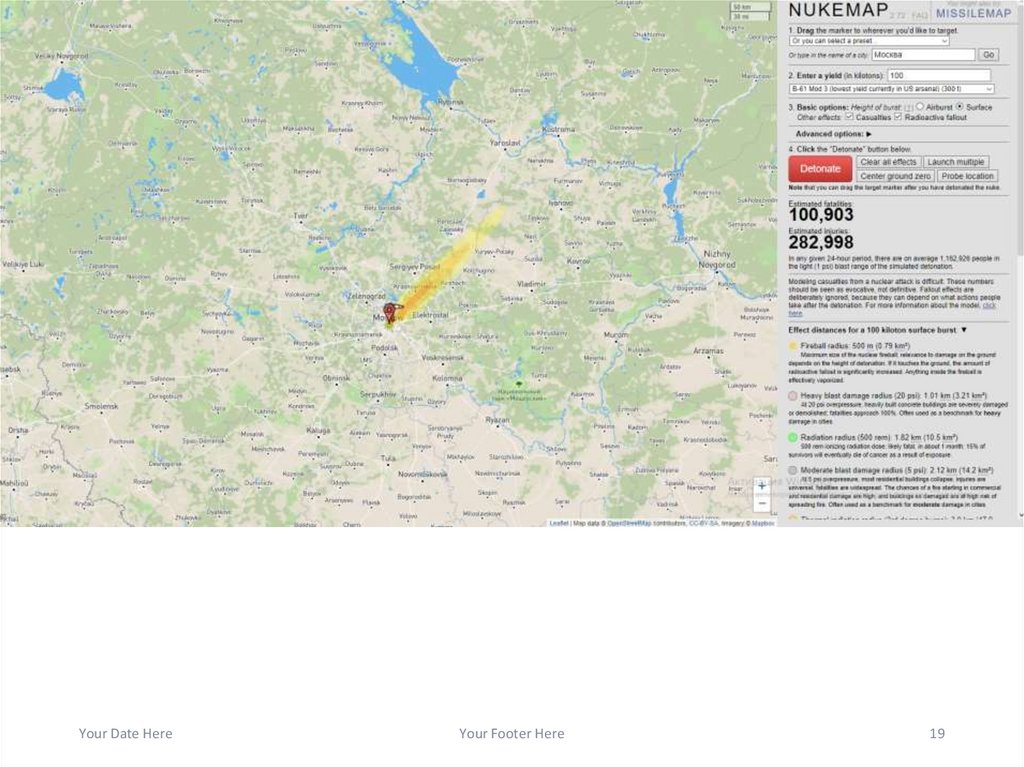
19.

Your Date Here
Your Footer Here
19

20.

THANK YOU !
Made with
by