Похожие презентации:
Решение второй основной задачи динамики точки
1. Решение второй основной задачи динамики точки
2.
nm x Fkx ( t , x , y, z , x , y, z )
1
n
(1.3) m y Fky ( t , x , y, z , x , y, z )
1
n
m z Fkz ( t , x , y, z , x , y , z )
1
x f 1 ( t ,C 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 )
y f 2 ( t ,C 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 )
z f ( t ,C ,C ,C ,C ,C ,C )
3
1
2
3
4
5
6
(1.3 )
(2.1)
Начальные условия движения:
при t t0
x x0 ; y y0 ; z z0 ;
x x0 ; y y0 ; z z0 .
(2.2)
3.
x f 1 ( t , x0 , y0 , z0 , x0 , y0 , z0 )y f 2 ( t , x0 , y0 , z0 , x0 , y0 , z0 )
z f ( t , x , y ,z , x , y ,z )
3
0
0 0
0
0 0
(2.3)
Под действием одной и той же силы материальная точка
может совершать целый класс движений, определяемых
начальными условиями движения.
Введением начальной скорости материальной точки
учитывается влияние на ее движение сил, действовавших на
точку до момента времени, принятого за начальный.
Уравнения (2.3) описывают движение точки до тех пор, пока
на нее действуют силы, вошедшие в правую часть
дифференциальных уравнений (1.3').
4. Примеры интегрирования дифференциальных уравнений движения материальной точки
5.
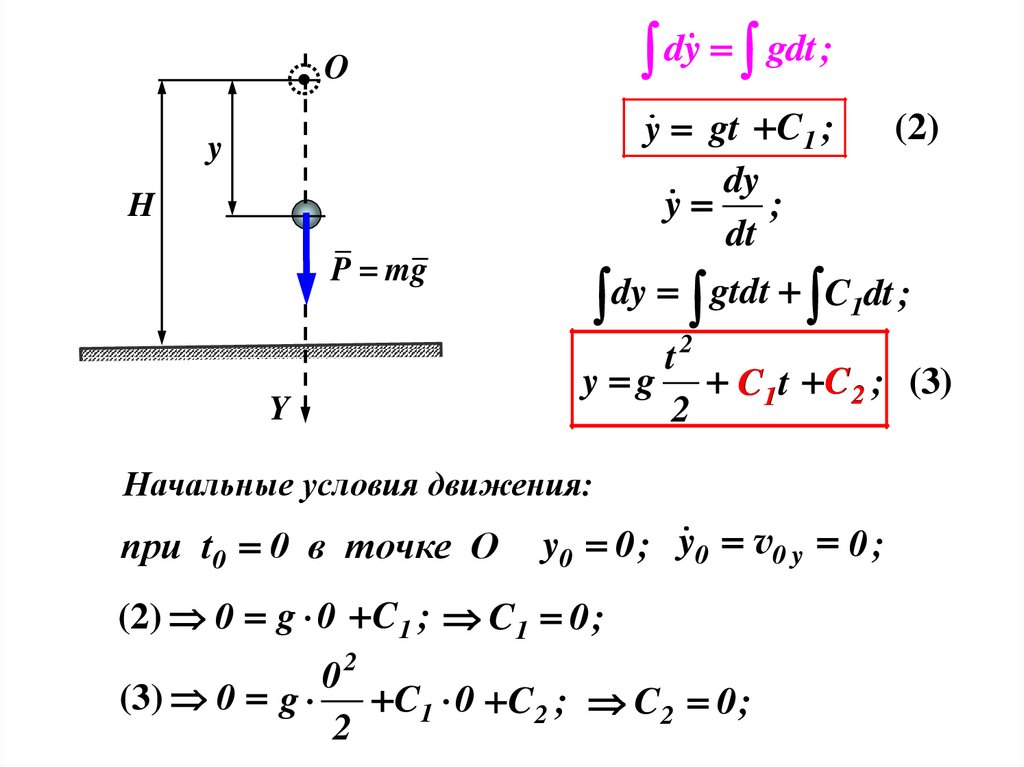
I) Случай постоянных сил (свободное падение тела без учетасопротивления воздуха)
Тело M падает с высоты Н без начальной скорости. Найти закон движения
тела. Сопротивлением воздуха пренебречь.
n
O
y
H
P mg
Y
(1.3 ) m y FkY ;
1
m
/ g;
/ y m
y g;
(1)
d dy dy
y
;
dt dt dt
dy
g;
dt
dy gdt ;
dy gdt ;
6.
dy gdt ;O
y gt C1 ;
dy
y
;
dt
y
H
P mg
Y
dy gtdt C1dt ;
t2
y g C1 t C 2 ; (3)
2
Начальные условия движения:
при t0 0 в точке О
(2)
y0 0; y0 v0 y 0 ;
(2) 0 g 0 C 1 ; C1 0;
02
(3) 0 g
C1 0 C 2 ; C2 0;
2
7.
Oy
y gt C1 ;
t2
y g C1t C 2 ;
2
(2)
(3)
Закон изменения проекции
скорости точки на ось Y:
H
P mg
А
y gt ;
(4)
Закон движения точки :
t2
y g ;
2
(5)
Y
1. Скорость свободно падающего тела пропорциональна
времени падения.
2. Расстояния, проходимые свободно падающим телом,
пропорциональны квадрату времени падения.
при t T в точке A
y yA H ;
T2
(5) H g
; T
2
2H
;
g
8.
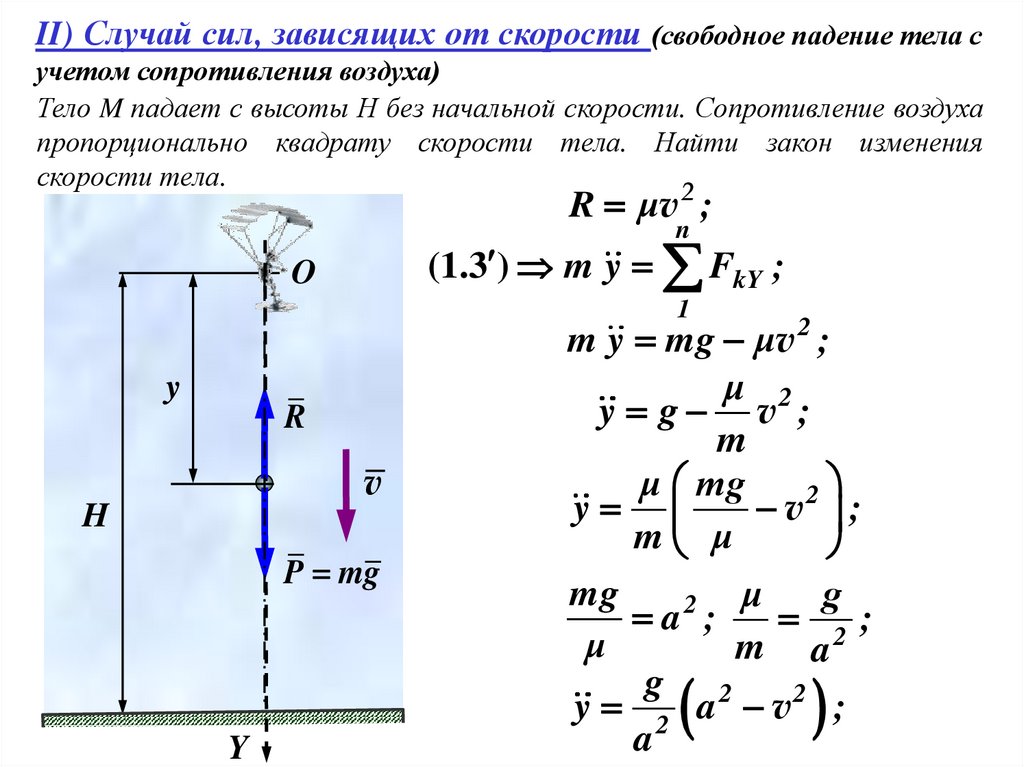
II) Случай сил, зависящих от скорости (свободное падение тела сучетом сопротивления воздуха)
Тело M падает с высоты Н без начальной скорости. Сопротивление воздуха
пропорционально квадрату скорости тела. Найти закон изменения
скорости тела.
R μv 2 ;
n
(1.3 ) m y FkY ;
O
1
y
R
v
H
P mg
Y
m y mg μv 2 ;
μ 2
y g v ;
m
μ mg
2
y
v ;
m μ
mg
μ
g
2
a ;
2;
μ
m a
g 2
y 2 a v2 ;
a
9.
dy d v y d vy
;
dt
dt
dt
dv g 2
2 a v2 ;
dt a
dv
g
dt ;
2
a
a v
2
2
1
a v g
ln
2 t C;
2a/ a v a /
a v 2g
ln
t C1 ; (1)
a v
a
Начальные условия движения:
при t0 0 в точке О
g 2
y 2 a v2 ;
a
y0 v0 y 0 ;
10.
a v 2gln
t C1 ; (1)
a v
a
a 0 2g
(1) ln
0 C1 ;
a 0
a
C1 ln 1 0 ;
a v 2g
(1) ln
t;
a v
a
2g
t
a v
e a ;
a v
2g
t
a
a v a v e ;
v a
2g
t
e a 1
2g
t
e a 1
;
(2)
(2) - закон зависимости скорости точки от времени.
11.
v aпри t
2g
t
e a
2g
t
e a 1
2g
t
e a 1
v vпред a
; (2)
mg
;
μ
Величина предельной скорости возрастает с увеличением
веса тела и уменьшением коэффициента сопротивления
среды.
12.
III) Случай сил, зависящих от положения точкиТочка M поднимается с поверхности Земли вертикально вверх с начальной
скоростью v0. Пренебрегая сопротивлением воздуха, найти закон
зависимости скорости точки от пройденного расстояния. Сила
притяжения точки к Земле изменяется по закону всемирного тяготения
Ньютона.
n
(1.3 ) m y FkY ;
Y
1
m y F ;
F
h
v0
y
R
O
mM
F k 2 ;
y
mM
/
m
y
k
;
/
2
y
M
y k 2 ;
y
13.
mM/
F k 2 mg;
/
R
при y R
Y
v
F
h
v0
y
R
O
M
y k 2 ;
y
2
kM gR ;
R2
y g 2 ; (1)
y
dv y
d v y dy d v y
dv
y
;
vy v
dt
dy dt
dy
dy
dv
R2
(1) v
g 2 ;
dy
y
gR 2
vd v
dy;
2
y
v 2 gR 2
C1 ; (2)
2
y
14.
v 2 gR 2C1 ; (2)
2
y
v
F
h
y
y0
v0
R
O
при t0 0 в точке A
v v0 ;
Y
A
Начальные условия движения:
y y0 R;
v02 gR /2
(2)
C1 ;
2
R/
v02
C1
gR;
2
v 2 gR 2 v02
(2)
gR;
2
y
2
2
2
gR
v2
v02 2 gR;
y
v
2 gR
2
v0
y R
y
;
15.
v2 gR
2
v0
y R
y
v
Y
v
F
h
A
y
y0
v0
R
O
y h R;
;
2gRh
2
v0
;
(3)
h R
при y hmax
v 0;
2gRhmax
2
v0
0;
hmax R
2gRhmax
v02 ;
hmax R
hmax
v02 R
2gR v02
;
16.
hmaxv02 R
;
2gR v02
точка
достигнет
некоторой
высоты hmax и упадет на Землю
Y
v
F
A
v0
y0
R
O
К содержанию курса
2 ) при v0 2gR
hmax ;
h
y
1 ) при v0 2gR
точка
будет
неограниченно
удаляться от поверхности Земли
км
2gR 11,2
с
- вторая космическая скорость.






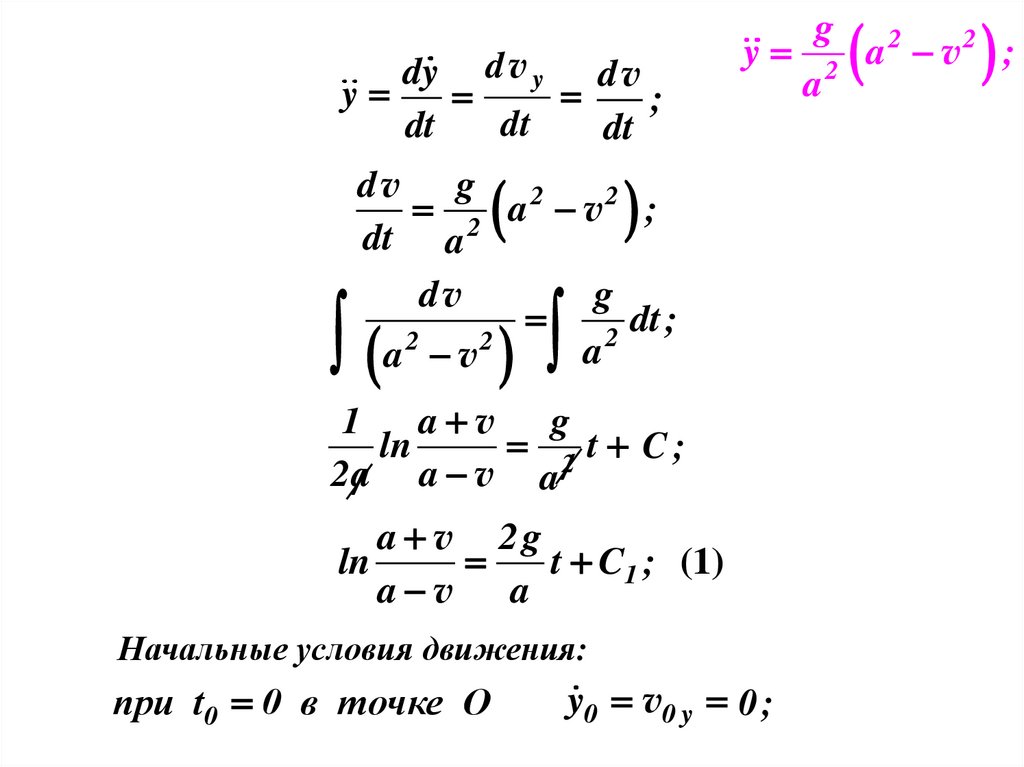







 Физика
Физика








