Взаимное положение двух прямых в пространстве. Угол между двумя прямыми

1. Взаимное расположение прямых в пространстве. Угол между двумя прямыми.

ВЗАИМНОЕ
РАСПОЛОЖЕНИЕ
ПРЯМЫХ В
ПРОСТРАНСТВЕ.
УГОЛ МЕЖДУ ДВУМЯ
ПРЯМЫМИ.

2. Взаимное расположение прямых в пространстве: 1. Параллельны 2. Пересекаются 3. Скрещиваются

ВЗАИМНОЕ
РАСПОЛОЖЕНИЕ ПРЯМЫХ
В ПРОСТРАНСТВЕ:
1. ПАРАЛЛЕЛЬНЫ
2. ПЕРЕСЕКАЮТСЯ
3. СКРЕЩИВАЮТСЯ

3. Расположение прямых в пространстве:

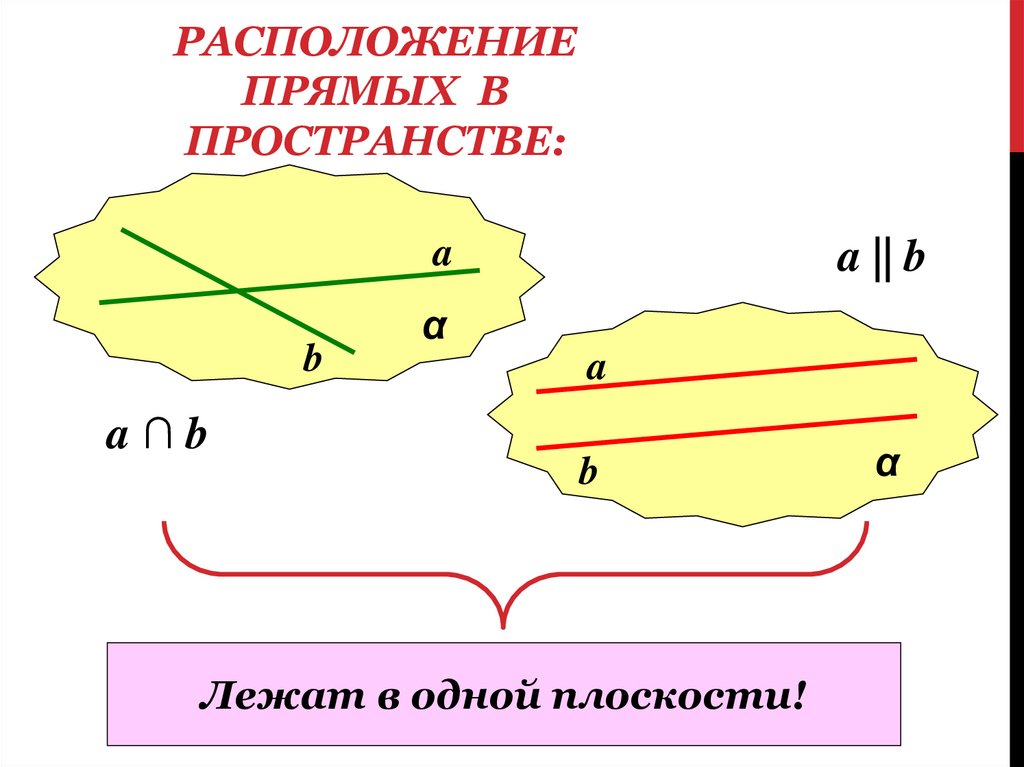
РАСПОЛОЖЕНИЕ
ПРЯМЫХ В
ПРОСТРАНСТВЕ:
a
b
a∩b
a || b
α
a
b
Лежат в одной плоскости!
α

4.

5.

a b
a
b

6.

Две прямые называются
скрещивающимися,
если они не лежат в одной плоскости.

7.

Теорема:
Если одна из двух прямых
лежит в некоторой плоскости,
а другая прямая пересекает
эту плоскость в точке, не
лежащей на первой прямой,
то эти прямые
скрещивающиеся

8. Признак скрещивающихся прямых.

ПРИЗНАК СКРЕЩИВАЮЩИХСЯ
ПРЯМЫХ.
a
b
Если одна из двух прямых лежит в
некоторой плоскости, а другая прямая
пересекает эту плоскость в точке, не
лежащей на первой прямой, то эти
прямые скрещивающиеся.

9. Теорема:

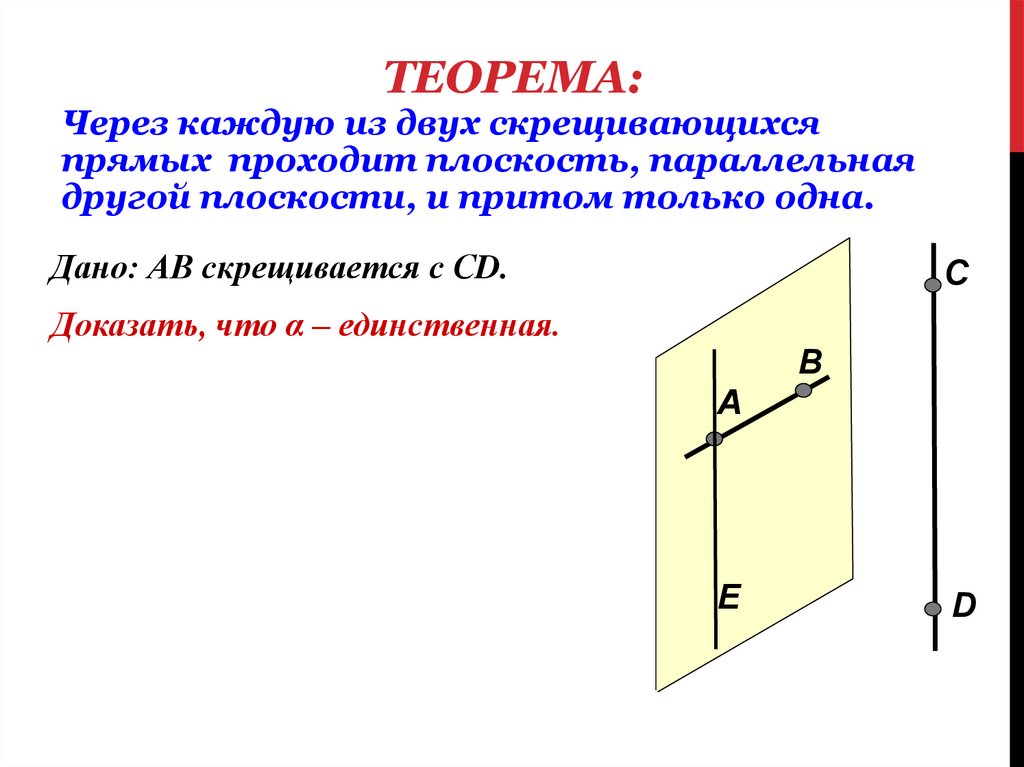
ТЕОРЕМА:
Через каждую из двух скрещивающихся
прямых проходит плоскость, параллельная
другой плоскости, и притом только одна.
Дано: АВ скрещивается с СD.
C
Доказать, что α – единственная.
В
А
Е
D

10.

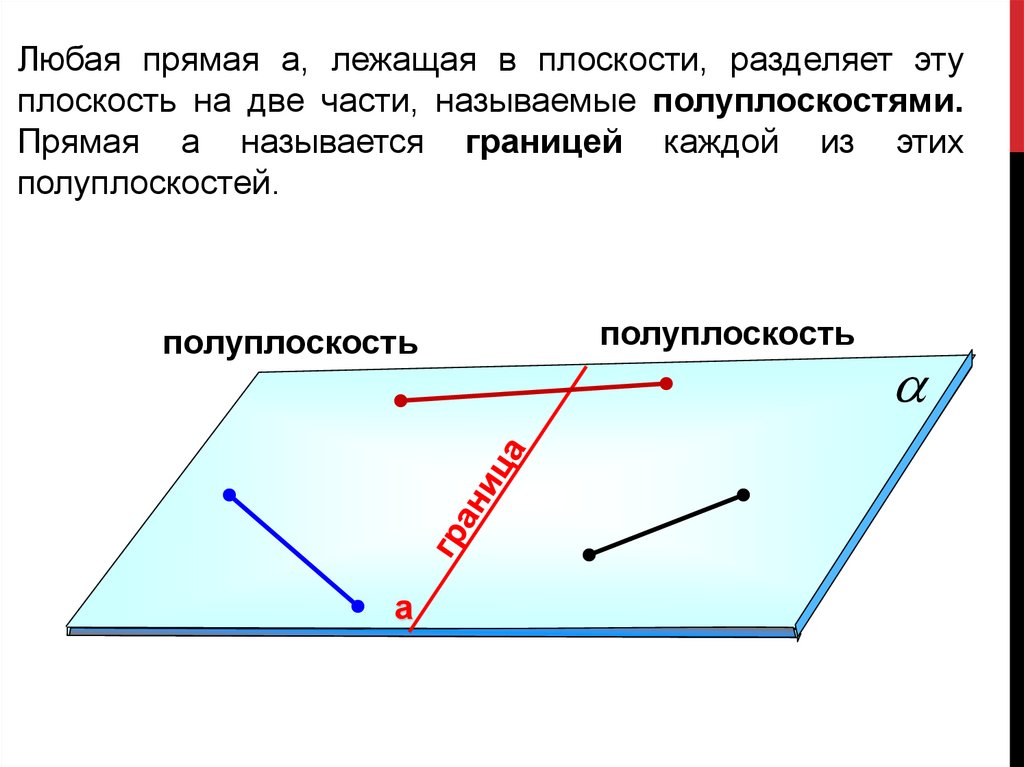
Любая прямая а, лежащая в плоскости, разделяет эту
плоскость на две части, называемые полуплоскостями.
Прямая а называется границей каждой из этих
полуплоскостей.
полуплоскость
а
полуплоскость

11.

A3
О3
A2
Углы с
сонаправленными
сторонами
О2
О1
A
A1
О
В2

12.

Теорема об углах с сонаправленными сторонами
Если стороны двух углов соответственно сонаправлены,
то такие углы равны.
A
О
B
A1
О1
B1

13. Угол между скрещивающимися прямыми.

1.
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ
ПРЯМЫМИ.
А
С
α
D
1800 - α
00 < α
900
В
А1
2.
Угол между
скрещивающимися
прямыми АВ и СD
определяется как угол
между пересекающимися
прямыми А1В1 и С1D1,
при этом А1В1|| АВ и С1D1|| CD.
α
М1
D1
В1
С1