Множественная линейная регрессия

1.

Множественная линейная регрессия
Если измеряемая случайная величина
зависит
y f ( x1, x2 ,..., x )
независимых переменных
k
то чаще всего ее можно описать с помощью полинома:
от
нескольких
y a0 a1x1 a2 x2 ... ak xk a12 x1x2 a13 x1x ... a1k x1x a x x ....
3
k 23 2 3
a x x x ... a x 2 a x 2 ... ...a x 3 ...
123 1 2 3
11 1
22 2
111 1
Всегда можно подобрать полином, достаточно близко описывающий
экспериментальную зависимость. Чем выше степень полинома, тем
больше экстремумов на кривой
Уравнение состояния Ван-дер-Ваальса для реального газа представляет
собой кубическое уравнение:
RT 2 a
a b
V V
V 3 b
0
p
p
p

2.

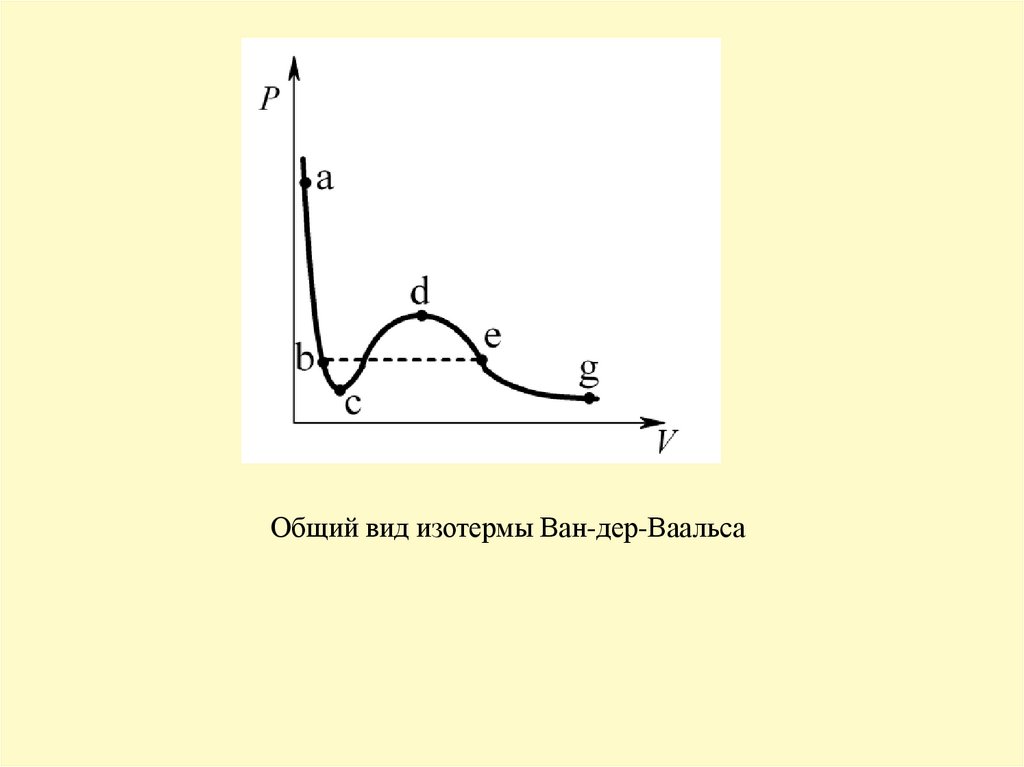
Общий вид изотермы Ван-дер-Ваальса

3.

Адекватности уравнения регрессии эксперименту добиваются
повышением степени полинома. Все коэффициенты a0 , a1,...ak
коррелировны между собой, поэтому при добавлении очередного
члена полинома все коэффициенты приходится рассчитывать
заново. Чтобы этого избежать, заранее рассчитывают
коэффициенты для полинома, заведомо более высокого порядка, а
затем незначимые коэффициенты отбрасывают.
Наибольший практический интерес представляют уравнения,
которые содержат только линейные слагаемые. Они представляют
собой уравнение множественной линейной регрессии:
y a0 x0 a1x1 a2 x2 ... ak xk
Зависимость теплового
выражается уравнением:
эффекта
реакции
от
температуры

4.

.
b 2 c
HT A aT
T
T
2
1
2
y a0 a1T a2T a3
T
y a0 x0 a1x1 a2 x2 a x
3 3
0
1
x0 f 0 (T ) 1 x1 f1(T );
2
x2 f 2 (T );
1
x3 f3
T
Это линейные функции соответствующих переменных
ai
- коэффициенты или параметры линейной регрессии
2
метод наименьших квадратов из условия ε ( y yˆ ) min
i
используем регрессионный анализ в матричной форме

5.

H
T1 400 K
T 500 K
2
T 600 K
3
H
H
…
T 400
T 500
T 4600
…
H T
Tj
j
j>l, где l – число коэффициентов в уравнении регресссии
Матрица независимых переменных
F
f0
1
f1 f 2
T1 T12
1
1
... ...
T j T j2
x 1 T
T2
σ 0 σ1 σ 2
H T
1
H T
2
Y
...
H T
f3
1
T1
...
1
Tj
1
T
σ3
Вектор наблюдений
j
где
σ1 σ(T ); σ 2 (T 2 ); σ3 σ( 1 )
T

6.

Вектор оценок определяемых коэффициентов в виде матрицыстолбца
a0
a1
aˆ
a2
a3
aˆ ( F F ) ( F Y )
T
1
T
FT − транспонированная матрица, полученная из матрицы F
заменой строк столбцами; (FTF) − это матрица, полученная
умножением транспонированной матрицы FT на исходную F

7.

T1
T12
1 T
T2
1 T3
T32
1
1
T
1
T
(F F ) T 2
1
1
T
1
j
j
Ti
i 1
j
2
Ti
i 1
j
1T
i 1 i
1
T2
1
T3
...
...
T22
1
T
T32
1
T
...
2
j
Ti
i 1
j
2
Ti
i 1
j
3
Ti
i 1
j
3
j
2
Ti
i 1
j
3
Ti
i 1
j
4
Ti
i 1
j
Ti
i 1
...
1
Tj
2
2
T j2
2
1
T
T
4
4
1
T ... ... ...
j
1 T j T j2
j
1T
i 1 i
j
j
Ti
i 1
j
1 2
i 1 T
1
T1
1
T
2
1
T3
1
T4
...
1
Tj

8.

диагональные члены матрицы FTF содержат суммы квадратов
переменных:
(T )
0 2
(Ti )
2
(Ti )
2 2
1 2
(T )
Эти величины отличаются на несколько порядков
(Ti )2 16 104 ... 169 104
2 2
8
2
8
(
T
)
256
10
...
169
10
i
1 2
(
T ) (2.5 10 3 )2 ... (7.69 10 4 )2 4 10 6 ... 5.9 10 7

9.

Матрица F1 из стандартизированных переменных и исключенным из нее
свободным членом
для интервала температур 400 − 1300К стандартизированная матрица
имеет вид
400 T
σ1
160000 T 2
σ2
500 T
F1
σ1
...
250000 T 2
σ2
...
1300 T
σ1
169 10 4 T 2
σ2
1
400
T
σ3
1
1
500
T
σ3
...
1
1
1300
T
σ3
1
H 400 H
σy
H 500 H
Y
σy
...
H1300 H
σy

10.

x11
x21
F1 x31
...
x j1
x12
x22
x32
...
x j2
x13
x23
x33
...
x j3
y11
y 21
Y y31
...
y j1
где первый индекс означает номер в столбце, второй − номер в
строке
aˆ F T F
1 1
1
F T Y
1
F T F
1 1
1
A
det F1T F1
A - взаимная матрица, состоящая из алгебраических дополнений
det F T F - определитель матрицы
1 1

11.

F T F
1 1
x11
x12
x13
x21
x22
x23
найдем
x y1 x
11
x y 2 x x21
x y 3 x y1
Алгебраическое дополнение
x
12
x
x
22
y2
j
2
x
i1
i
1
x
j
13
x xi 1 xi 2
23
i 1
x
j
y3
xi 3 xi 1
i 1
j
xi 1 xi 2
i 1
j
2
xi 2
i 1
j
xi 2 xi 3
i 1
Д ik ( 1) i k det M ik
j
xi 1 xi 3
i 1
j
xi 2 xi 3
i 1
j
2
xi 3
i 1

12.

j
2
xi1
i 1
j
xi1 xi 2
i 1
j
xi 3 xi1
i 1
1 2 3
A 4 5 6
7 8 9
2
x
1 ( 1)1 1 det 2
x3 x2
2=
j
xi1 xi 2
i 1
j
2
xi 2
i 1
j
xi 2 xi 3
i 1
j
xi1 xi 3
i 1
j
xi 2 xi 3
i 1
j
2
xi 3
i 1
x 2 x3 ( x 2 x 2 ( x x ) 2 )
j2
j3
j 2 j3
2
x
3
x j 2 x j1 x 2j 3 x j 3 x j1 x j 2 x j 3
3 x j 2 x j1 x x j 3 x j1 x j 2 x j 3
2
j3

13.

вычислим
j
2
xi1
i 1
j
xi1 xi 2
i 1
j
xi 3 xi1
i 1
det( F1T F1 )
j
xi1 xi 2
i 1
j
2
xi 2
i 1
j
xi 2 xi 3
i 1
Разложим матрицу по первой строке:
j
xi1 xi 3
i 1
j
xi 2 xi 3
i 1
j
2
xi 3
i 1
det( F1T F1 ) xi21 1 xi1xi 2 2 xi1xi 3 3

14.

*
A
( F1T F1 ) 1
det( F1T F1 )
T
1
( F F1 )
1
Найдем вектор
det( F F ) const
T
1 1
матрица ошибок или ковариационная матрица
( F1T Y )
x11
( F1T Y ) x12
x13
x21
x22
x23
y11 xi1 y j1
... x j1 y21
... x j 2 y31 = xi 2 y j 2
... x j 3 ...
y x y
i3 j3
j1

15.

где
И, наконец, вычислим оценки коэффициентов уравнения регрессии:
x
y
i1 j1
a1
1 2 3
1
a
4 5 6 xi 2 y j 2 a2 ,
T
det( F1 F1 )
7 8 9
a3
xi 3 y j 3
1
;
a1
x
y
(4)
x
y
(2)
x
y
(3)
i1 i1
i 2 i1
i 3 i1
T
det( F1 F1 )
a2
a3
1
;
x
y
(4)
x
y
(5)
x
y
(6)
i1 i1
i 2 i1
i 3 i1
T
det( F1 F1 )
1
.
x
y
(7)
x
y
(8)
x
y
(9)
i1 i1
i 2 i1
i 3 i1
T
det( F1 F1 )

16.

Найдем истинные значения коэффициентов уравнения
(в натуральном масштабе)
y
*
a1 a1
1
y
*
a2 a2
2
y
a a3
3
*
3
a0* y a1* T a2* T 2 a3* 1
T

17.

Статистическая обработка результатов
1
A
1
T
1
( F1 F1 )
4
T
T
det( F1 F1 ) det( F1 F1 )
7
*
c11 c12
( F1T F1 ) 1 c21 c22
c31 c32
2 3
5
6
8 9
c13
c23
c33

18.

Дисперсии определения коэффициентов
a21 c11 y2
2
2
2
ai cii y a2 c22 y2
2
2
a3 c33 y
(1)
c11
det( F1T F1 )
Cova1a2 c12
(5)
c22
det( F1T F1 )
2
y
Cova2a3 c23
c33
2
y
(9)
det( F1T F1 )
Cova1a3 c13 y2

19.

Ранжировка коэффициентов
ti
ai
S y cii
Проверка адекватности модели
2
S
F расч 2 ад
S1 ( y )
S ад2
F
1
2
ˆ
(
y
y
)
i
n l
расч
F
крит
f ад , f y ,1 p
S12 ( y )
1
( yi y )2
n 1
Модель адекватна, если F расч Ff крит
,
, f ,1 p
ад
y

20.

F
расч
1
1
F
расч
Ff n 1, f n l ,1 p
y
ад
Оценка тесноты связи
2
(n-l)Sад2
ˆ
(
y
y
)
i
ξ
(n-1 )S12 y ( yi y ) 2
Чем ближе
1
1 ξ
, тем теснее связь.
Величина называется корреляционным отношением