Похожие презентации:
Избранные главы математики
1. Избранные главы математики
Лекция №1 и 2-32. Содержание
Основные понятия теории вероятностейТеоремы сложения, умножения вероятностей
Формула полной вероятности. Формула Бейеса
Повторение испытаний. Формула Бернулли
Cлучайная величина. Законы распределения. Функция распределения
Закон распределения дискретной случайной величины
Аналитическое задание закона распределения
Интегральная функция распределения
Дифференциальная функция распределения
Равномерное распределение непрерывной случайной величины
Числовые характеристики случайных величин
Нормальный закон распределения вероятностей непрерывной
случайной величины
3.
Определение. Вероятностью события Аназывается
математическая
оценка
возможности появления этого события в
результате опыта. Вероятность события А равна
отношению
числа,
благоприятствующих
событию А исходов опыта к общему числу
попарно
несовместных
исходов
опыта,
образующих полную группу событий.
Определение. Событием называется всякий
факт, который может произойти или не
произойти в результате опыта .
4.
Определение. Полной группой событийназывается совокупность всех возможных
результатов опыта.
Определение. Достоверным событием
называется событие, которое наверняка
произойдет в результате опыта. Событие
называется невозможным, если оно никогда
не произойдет в результате опыта.
5.
Определение. Относительной частотойсобытия А называется отношение числа опытов, в
результате которых произошло событие А к
общему числу опытов.
Отличие относительной частоты от вероятности
заключается в том, что вероятность вычисляется
без непосредственного произведения опытов, а
относительная частота – после опыта.
При достаточно большом числе произведенных
опытов относительная частота изменяется мало,
колеблясь около одного числа. Это число может
быть принято за вероятность события.
6.
Определение. Элементарными исходами опытаназываются такие результаты опыта, которые
взаимно исключают друг друга и в результате опыта
происходит одно из этих событий, также каково бы
ни было событие А, по наступившему
элементарному исходу можно судить о том,
происходит или не происходит это событие.
Совокупность всех элементарных исходов опыта
называется пространством элементарных
событий.
7.
Теоремы сложения, умножения вероятностейТеорема (сложения вероятностей).
Вероятность суммы двух несовместных событий
равна сумме вероятностей этих событий.
P( A B) P( A) P( B)
Следствие 1: Если события образуют полную
группу несовместных событий, то сумма их
вероятностей равна единице.
n
P( A ) 1
i 1
i
8.
Определение. Противоположными называютсядва несовместных события, образующие полную
группу.
Теорема. Вероятность появления хотя бы одного
из двух совместных событий равна сумме
вероятностей этих событий без вероятности их
совместного появления.
P( A B) P( A) P( B) P( AB)
Следствие 2: Сумма вероятностей
противоположных событий равна единице.
P( A) P( A ) 1
9.
Определение.Событие
А
называется
независимым от события В, вероятность
события А не зависит от того, произошло
событие В или нет. Событие А называется
зависимым
от
события В,
если
вероятность
события
А
меняется
в
зависимости от того, произошло событие В
или нет.
10.
Определение. Вероятность события В, вычисленнаяпри условии, что имело место событие А, называется
условной вероятностью события В.
PA ( B) P( B / A) P( AB) / P( A)
Теорема. (Умножения вероятностей) Вероятность
произведения двух событий (совместного появления
этих событий) равна произведению вероятности
одного из них на условную вероятность другого,
вычисленную при условии, что первое событие уже
наступило.
P( AB) P( A) P( B / A) P( A) PA ( B)
11.
Если события независимые, то P ( B / A) P ( B ), и теоремаумножения вероятностей принимает вид:
P( AB) P( A) P( B)
Если в результате испытания может появиться n событий,
независимых в совокупности, то вероятность появления
хотя бы одного из них равна
P( A) 1 q1q2 ...qn
Здесь событие А обозначает наступление хотя бы одного
из событий Ai, а qi – вероятность противоположных
событий
.
A1 , A2 ,..., An
12. Формула полной вероятности. Формула Бейеса
Пусть некоторое событие А может произойтивместе с одним из несовместных событий
H 1 , H 2 ,..., H n , составляющих полную группу
событий. Пусть известны вероятности этих
событий P( H1 ), P( H 2 ),..., P( H n ) и условные
вероятности наступления события А при
наступлении события Hi
P( A / H 1 ), P( A / H 2 ),..., P( A / H n )
13.
Теорема. Вероятность события А, которое может произойтивместе с одним из событий , равна сумме парных произведений
вероятностей каждого из этих событий на соответствующие им
условные вероятности наступления события А.
n
P( A) P( H i ) P( A / H i )
i 1
Пусть имеется полная группа несовместных гипотез H 1 , H 2 ,..., H n
с известными вероятностями их наступленияP( H 1 ), P( H 2 ),..., P( H n ).
Пусть в результате опыта наступило событие А, условные вероятности
которого по каждой из гипотез известны, т.е. известны вероятности
.
P( A / H 1 ), P( A / H 2 ),..., P( A / H n )
Требуется определить какие вероятности имеют гипотезы
относительно события А, т.е. условные вероятности
H 1 , H 2 ,..., H n
P( H i / A)
14.
Теорема. Вероятность гипотезы после испытания равнапроизведению вероятности гипотезы до испытания на
соответствующую ей условную вероятность события,
которое произошло при испытании, деленному на полную
вероятность этого события.
P( H i / A)
P( H i ) P( A / H i )
n
P( H ) P( A / H )
i 1
Эта формула называется
i
i
формулой Бейеса.
15. Повторение испытаний. Формула Бернулли
• Если производится несколько испытаний, причем вероятностьсобытия А в каждом испытании не зависит от исходов других
испытаний , то такие испытания называют независимыми
относительно события А.
• Будем предполагать далее, что Р(А) = р, т.е. вероятность р всегда
одинакова (0 < р < 1), и поставим задачу вычислить вероятность
того, что при n испытаниях событие А осуществится ровно k раз.
Ответ на этот вопрос дает формула Бернулли
• Вероятность того, что в n независимых испытаниях ( в каждом из
которых вероятность Р(А) = р одинакова ) событие А наступит
ровно k раз ( в любой последовательности), равна
Pn (k ) C p q
k
n
k
n k
16.
гдeВ частности
n!
C
k!(n k )!
k
n
C 1, C n, C C
0
n
1
n
k
n
n k
n
Вероятность того, что в n испытаниях
I)Событие А наступит менее k раз
PI P n (0) P n (1) ... P n (k 1)
PII P n (0) P n (1) ... P n (k )
II) Событие А наступит не более k раз
III) Событие А наступит более k раз PIII P n (k 1) P n (k 2) ... P n (n)
IV) Событие А наступит не менее k раз
PIV P n (k ) P n (k 1) ... P n (n)
17. Cлучайная величина. Законы распределения. Функция распределения
Случайной называют величину, которая врезультате испытания примет одно и только
одно возможное значение, наеред
неизвестное и зависящее от случайных
причин, которые заранее не могут быть
учтены.
Обозначим: X, Y, Z – случайные величины
xi , yi , zi – возможные значения случайных
величин
18.
Дискретной (прерывной) называют случайную величину,которая принимает отдельные возможные значения с
определенными вероятностями.
Непрерывной называют случайную величину, которая
может принимать все значения из некоторого конечного или
бесконечного промежутка. Число возможных значений
непрерывной случайной величины, независимо от величины
промежутка, бесконечно.
Для задания дискретной случайной величины недостаточно
перечислить все ее возможные значения, нужно указать еще и
их вероятность.
Вероятность (Р) показывает степень возможности
осуществления данного события, явления, результата.
19. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величиныназывают соответствие между ее возможными
значениями и вероятностями их появления. Закон
распределения можно задать таблично, аналитически (в
виде формулы) и графически (в виде многоугольника
распределения).
Табличное задание закона распределения:
X
P
x1 x2 ...xn - возможные значения случайной величины;
p1 p2 ... pn - вероятности появления случайной величины.
20. Аналитическое задание закона распределения:
Биномиальное распределение, определяемоезаконом Бернулли
Pn k Cnk pk qn k
k = 0, 1, 2, …, n – количество возможных появлений
событий
q = 1-p – вероятность не появления событий
Распределение Пуассона, определяемое
асимптотической формулой Пуассона:
Pn (k )
где
k e
k!
- интенсивность потока событий.
21.
Графическое задание закона распределенияпредставлено на рис. 1
Рис. 1 Полигон распределения дискретной
случайной величины.
22.
Способ описания распределения случайной величины в видетаблицы, в виде формулы или графически применим только
для дискретных случайных величин.
Интегральная функция распределения
Интегральная функция распределения позволяет задать как
дискретную, так и непрерывную случайную величину.
Интегральная функция распределения (ИФР) – это функция F(x),
определяющая для каждого возможного значения x
вероятность того, что случайная величина X примет значение
меньшее x, т. е.
F ( x) P( X x)
23.
Геометрический смысл интегральной функции распределения – этовероятность того, что случайная величина X примет значение,
которое на числовой оси лежит левее точки x.
Свойства интегральной функции распределения:
1. Значения интегральной функции распределения принадлежат
отрезку [0;1] :
0 F ( x) 1
2. Вероятность того, что случайная величина X примет значение,
заключенной в интервале (a,b), равна приращению интегральной
функции распределения на этом интервале
P(a X b) F (b) F (a)
3. Если все возможные значения x случайной величины принадлежат
интервалу (a, b), то
F ( x) 0
, если
x a
F ( x) 1
, если
x b
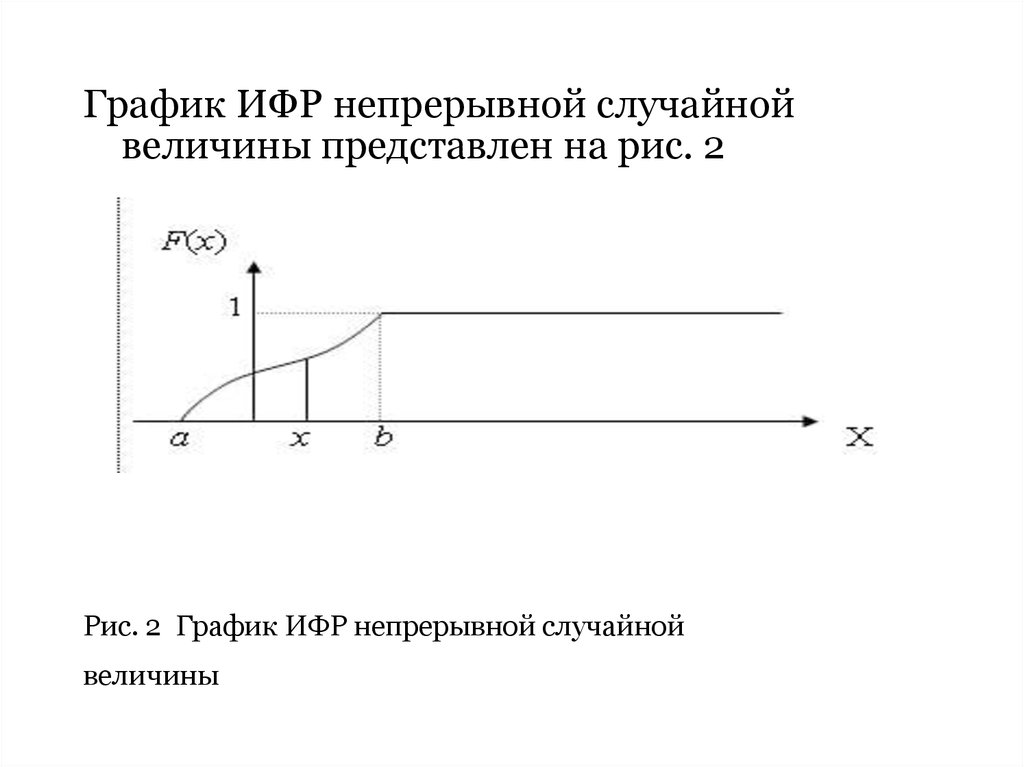
24.
График ИФР непрерывной случайнойвеличины представлен на рис. 2
Рис. 2 График ИФР непрерывной случайной
величины
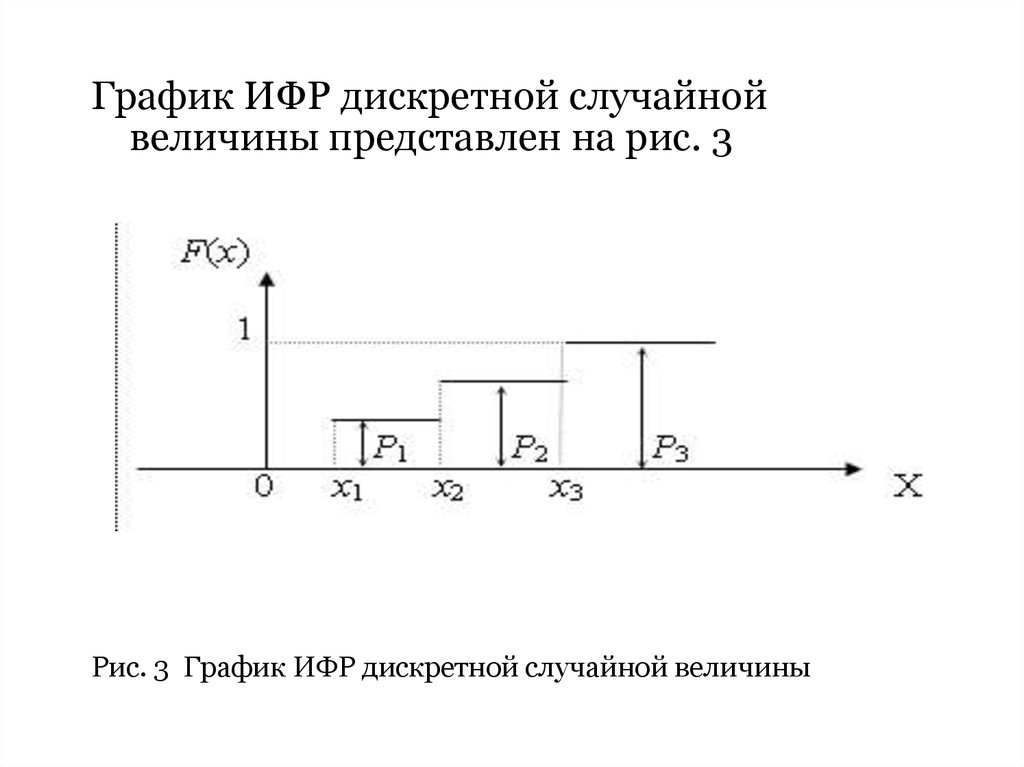
25.
График ИФР дискретной случайнойвеличины представлен на рис. 3
Рис. 3 График ИФР дискретной случайной величины
26. Дифференциальная функция распределения
Для описания распределения вероятностей непрерывной случайнойвеличины используется дифференциальная функция
распределения.
Дифференциальная функция распределения (ДФР) (или плотность
вероятности) – это первая производная от интегральной
функции.
f ( x) F ( x)
Интегральная функция распределения является первообразной для
дифференциальной функции распределения. Тогда
x
F ( x) f ( x)dx P( X x)
Вероятность того, что непрерывная
случайная величина X примет
значение, принадлежащее интервалу (a,b), равна определенному
интегралу от дифференциальной bфункции, взятому в пределах от a
до b:
P(a X b) f ( x)dx
a
27.
Геометрический смысл ДФР состоит в следующем: вероятность того,что непрерывная случайная величина X примет значение,
принадлежащее интервалу (a, b), равна площади криволинейной
трапеции, ограниченной осью x, кривой распределения f(x) и
прямыми x = a и x = b (рис. 4).
Рис. 4 График дифференциальной функции распределения принято
называть кривой распределения.
28. Свойства дифференциальной функции распределения:
1. Дифференциальная функция распределения неотрицательна, т. е.f ( x) 0
2. Если все возможные значения случайной величины принадлежат
интервалу (a, b), то
b
f ( x)dx 1
a
Дифференциальную функцию распределения часто называют законом
распределения вероятностей непрерывных случайных величин.
29.
Прирешении
прикладных
задач
сталкиваются с различными законами
распределения вероятностей непрерывных
случайных величин. Часто встречаются
законы
равномерного
нормального распределения.
и
30. Равномерное распределение непрерывной случайной величины
Законравномерного
распределения
вероятностей
непрерывной
случайной
величины используется при имитационном
моделировании сложных систем на ЭВМ
как первоначальная основа для получения
всех необходимых статистических моделей.
При этом, если специально не оговорен
закон распределения случайных чисел, то
имеют ввиду равномерное распределение.
31.
Распределение вероятностей называют равномерным, если наинтервале (a,b), которому принадлежат все возможные значения
случайной величины, дифференциальная функция распределения
имеет постоянное значение, т. е. f(x) = C.
Так как
то
b
b
a
a
f ( x)dx Cdx 1,
C
1
b
dx
1
b a
a
Отсюда закон равномерного распределения аналитически можно
записать так:
0, x a,
1
f ( x)
, a x b,
b a
0, x b.
32.
График дифференциальной функции равномерногораспределения вероятностей представлен на рис.5
Рис. 5 График дифференциальной функции равномерного
распределения вероятностей.
33.
Интегральную функцию равномерногораспределения аналитически можно записать так:
0, если
x a, т.к.
f ( x) 0;
b
1
x a
x a
F ( x)
, если a x b, т.к. F ( x)
dx
;
b a
b a
a
b a
b a
x b, т.к.
F ( x)
1.
1, если
b a
34.
График интегральной функции равномерногораспределения вероятностей представлен на рис. 6
Рис. 6 График интегральной функции равномерного
распределения вероятностей.
35. Числовые характеристики случайных величин
Закон распределения полностью характеризуетслучайную величину. Однако часто закон распределения
неизвестен и приходится пользоваться, так
называемыми, числовыми характеристиками случайной
величины. К ним относятся:
1.математическое ожидание M;
2.дисперсия D;
3.среднее квадратичное отклонение
.
36.
Математическое ожидание дискретной случайной величины X –это сумма произведений всех ее возможных значений
xi , i 1,..., n
на их вероятности
pi , i 1,..., n
M ( X ) x1 p1 x2 p2 ... xn pn
Математическое ожидание непрерывной случайной величины
X, возможные значения которой принадлежат отрезку [a,b] –
это определенный интеграл
b
M ( X ) x f ( x)dx
a
37.
Математическое ожидание случайной величины (какдискретной, так и непрерывной) есть неслучайная
(постоянная) величина. Она характеризует среднее
значение случайной величины.
Свойства математического ожидания:
1.M(C)=C – математическое ожидание константы равно
самой константе
2.M (C X ) C M ( X )
3. M ( X Y ) M ( X ) M (Y )
4.M(X+Y)=M(X)+M(Y)
38.
Дисперсия и среднее квадратичное отклонение – это числовыехарактеристики случайной величины, которые позволяют оценить,
как рассеяны возможные значения случайной величины вокруг ее
математического ожидания.
Отклонением называют разность между значением случайной
величины и ее математическим ожиданием, т. е.
xi M ( X )
Пусть закон распределения дискретной случайной величины известен:
Так как одни возможные отклонения положительны, а другие
отрицательны, то математическое ожидание отклонения обладает
важным свойством:
M(X – M(X))=0, т.е. математическое ожидание отклонения всегда равно
нулю.
Поэтому для оценки рассеяния случайной величины вокруг ее
математического ожидания вычисляют квадрат отклонения
случайной величины.
39.
Дисперсией (рассеянием) случайной величины (как дискретной, так инепрерывной) называют математическое ожидание квадрата
отклонения случайной величины от ее математического ожидания.
Для дискретной случайной величины: D(X) = M(х – M(X))2
Для вычисления дисперсии часто бывает удобно пользоваться следующей
формулой: D(X)=M(X2)–(M(X))2, т.е. дисперсия равна разности
между математическим ожиданием квадрата случайной величины и
2
квадратом ее математического ожидания.
b
Для непрерывной случайной величины: D( X ) x M ( X ) f ( x )dx
a
В последнем выражении все возможные значения случайной величины
принадлежат отрезку (a, b).
Дисперсия случайной величины (как дискретной, так и случайной) есть
неслучайная величина (постоянная величина).
Свойства дисперсии:
1. D (C) = 0
2. D (CX) = С2 D (X)
3. D (X+Y) = D (X) + D (Y),
4. D (C+X) = D (X),
5. D (X-Y) = D (X) – D (Y).
40. «Нормальный закон распределения вероятностей непрерывной случайной величины»
Законнормального
распределения
вероятностей
непрерывной
случайной
величины занимает особое место среди
различных теоретических законов, т. к.
является основным во многих практических
исследованиях.
Им
описывается
большинство
случайных
явлений,
связанных
с
производственными
процессами.
41.
К случайным явлениям, подчиняющимся нормальному законураспределения, относятся ошибки измерений производственных
параметров, распределение технологических погрешностей
изготовления, рост и вес большинства биологических объектов и др.
Нормальным называют закон распределения вероятностей
непрерывной случайной величины, который описывается
дифференциальной функцией
1
f ( x)
e
2
2
x a
2 2
, где
a - математическое ожидание случайной величины;
-среднее квадратичное отклонение нормального распределения.
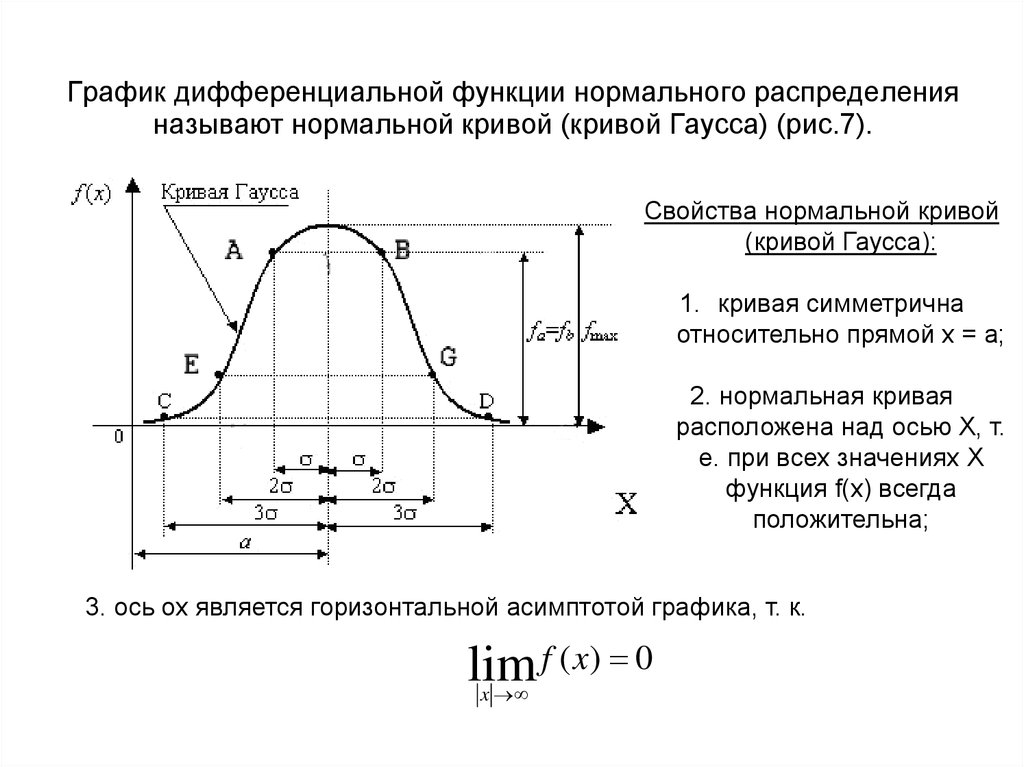
42. График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса) (рис.7).
Свойства нормальной кривой(кривой Гаусса):
1. кривая симметрична
относительно прямой x = a;
2. нормальная кривая
расположена над осью X, т.
е. при всех значениях X
функция f(x) всегда
положительна;
3. ось ox является горизонтальной асимптотой графика, т. к.
lim f ( x) 0
x
43.
4. при x = a функция f(x) имеет максимум равныйf max
1
0, 4
2
в точках A и B приx a и x
ординаты которых равны.
a
кривая имеет точки перегиба,
1
0, 24
f A fB
0, 6 f max
2 e
При этом, вероятность того, что абсолютная величина отклонения
случайной величины, распределенной нормально, от ее
математического ожидания не превысит среднего квадратичного
отклонения , равна 0,6826.
44.
в точках E и G, при x a 2и , x a 2
значение функции f(x) равно
1
0,05
2
f E fG
e
,
2
а вероятность того, что абсолютная величина отклонения
случайной величины, распределенной нормально, от
ее математического ожидания не превысит удвоенного
среднего квадратичного отклонения, равна 0,9544 .
45.
Асимптотически приближаясь к оси абсцисс, кривая Гаусса в точках C иD, при x a 3 и x a 3 , очень близко подходит к оси
абсцисс. В этих точках значение функции f(x) очень мало
1
fC f D
e
2
9
2
0,0044
,
а вероятность того, что абсолютная величина отклонения случайной
величины, распределенной нормально, от ее математического
ожидания не превысит утроенного среднего квадратичного
отклонения, равна 0,9973. Это свойство кривой Гаусса называется
"правило трех сигм".
46.
Еслислучайная
величина
распределена
нормально, то абсолютная величина ее
отклонения
от
математического
ожидания не превосходит утроенного
среднего квадратического отклонения.
Изменение
величины
параметра
a
(математического
ожидания
случайной
величины) не изменяет форму нормальной
кривой, а приводит лишь к ее смещению вдоль
оси X: вправо, если a возрастает, и влево, если
a убывает.
47.
При a=0 нормальная кривая симметрична относительно осиординат.
Изменение величины параметра
( среднего
квадратичного отклонения) изменяет форму нормальной
кривой : с возрастанием
ординаты нормальной
кривой убывают, кривая растягивается вдоль оси X и
прижимается к ней. При убывании
ординаты
нормальной кривой увеличиваются, кривая сжимается
вдоль оси X и становится более "островершинной".
48.
При этом, при любых значениях и площадьограниченная нормальной кривой и осью X, остается
равной единице (т. е. вероятность того, что случайная
величина, распределенная нормально, примет значение
ограниченное на оси X нормальной кривой, равна 1).
Нормальное распределение с произвольными параметрами
и , т. е. описываемое дифференциальной функцией
1
f ( x)
e
2
2
x a
2 2
называется общим нормальным распределением.
49.
Нормальное распределение с параметрами 0 и 1называется нормированным распределением (рис. 8). В
нормированном распределении дифференциальная функция
распределения равна:
f max 0, 4; f A f B 0, 24; fC f D 0,0044; f E fG 0,05.
Рис. 8 Нормированная кривая
50.
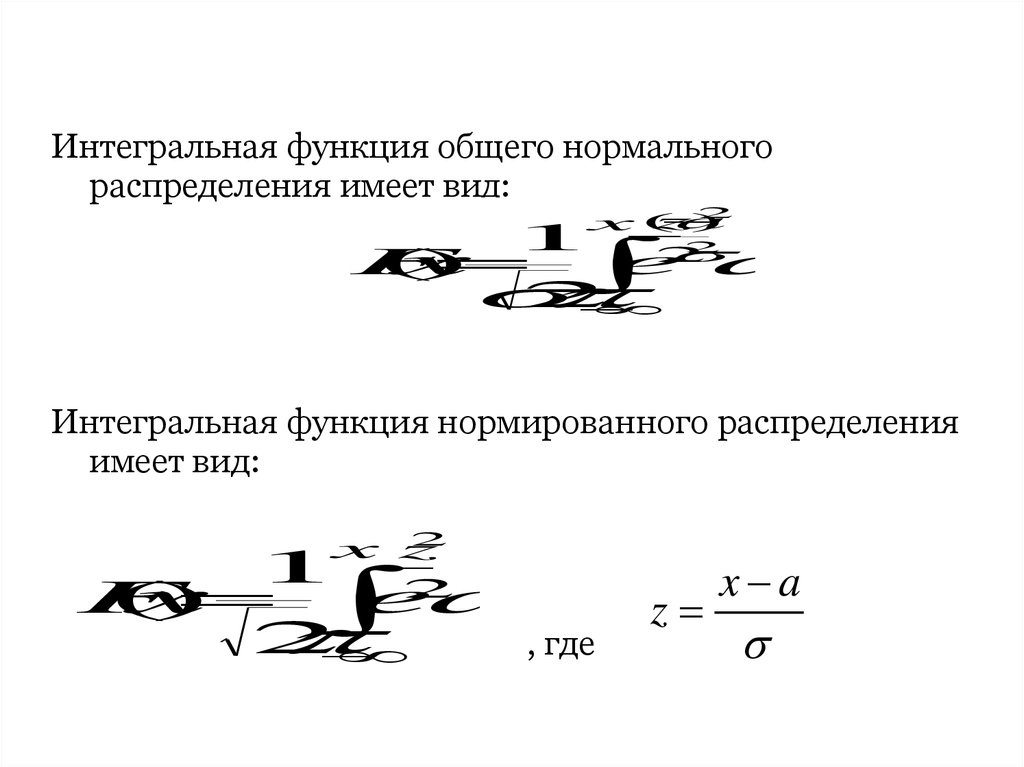
Интегральная функция общего нормальногораспределения имеет вид:
z
a
)
x(
2
2
2
1
F
(
x
)
e dz
2
Интегральная функция нормированного распределения
имеет вид:
2
x z
2
1
F
(
x
)
edz
2
, где
z
x a
51.
Пусть случайная величина X распределена понормальному закону в интервале (c, d). Тогда
вероятность того, что X примет значение,
принадлежащее интервалу (c, d) равна
P (c X d ) Ф (
d a
) Ф(
c a
)
52.
Пример. Случайная величина X распределена понормальному закону. Математическое ожидание и
среднее квадратичное отклонение этой случайной
величины равны a=30 и 10. Найти вероятность того,
что X примет значение в интервале (10, 50).
Решение:
По условию: c 10; d 50; а 30; 10 . Тогда
50 30 10 30
Р(10 X 50) Ф
Ф
Ф(2) Ф( 2) 2 Ф(2)
10 10
Пользуясь готовыми таблицами Лапласа (см. приложение
3), имеем:
Р(10 X 50) 2 0, 4772 0,9544
















































 Математика
Математика








