Похожие презентации:
Второй и третий признаки подобия треугольников
1. ВТОРОЙ И ТРЕТИЙ ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
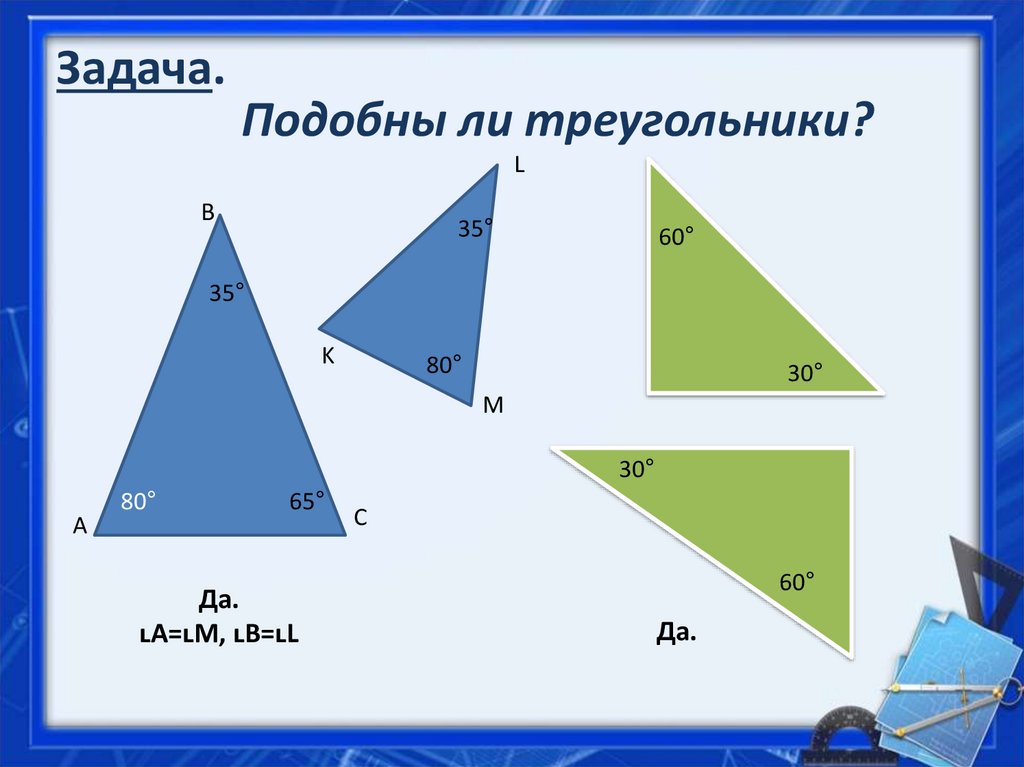
2. Задача.
Подобны ли треугольники?L
В
35°
60°
35°
K
80°
30°
M
30°
А
80°
65°
Да.
ʟА=ʟМ, ʟВ=ʟL
С
60°
Да.
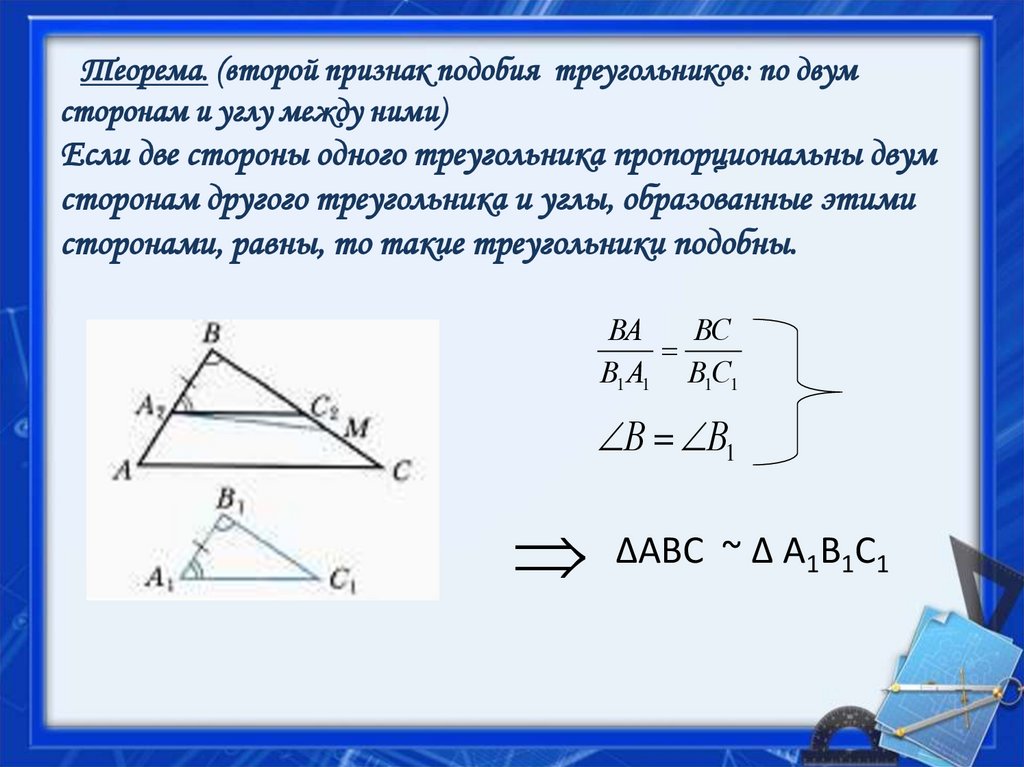
3. Теорема. (второй признак подобия треугольников: по двум сторонам и углу между ними) Если две стороны одного треугольника
пропорциональны двумсторонам другого треугольника и углы, образованные этими
сторонами, равны, то такие треугольники подобны.
ВА
ВС
В1 А1 В1С1
В В1
ΔАВС ~ Δ А В С
1 1 1
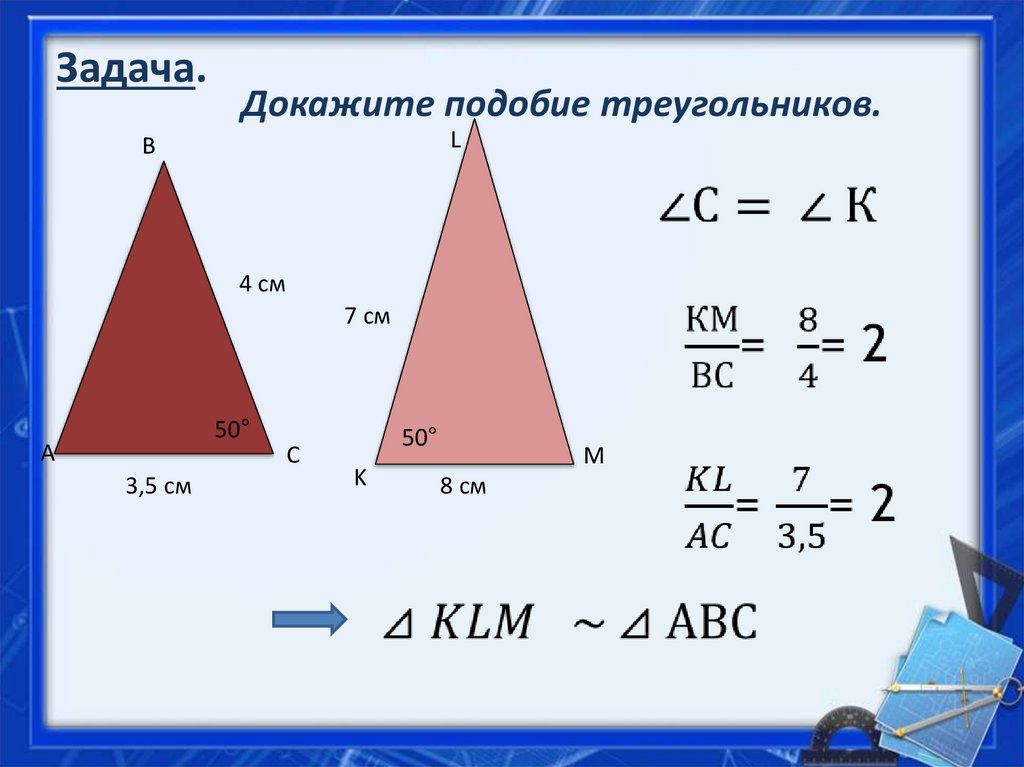
4. Задача.
Докажите подобие треугольников.L
В
4 см
7 см
50°
А
3,5 см
С
50°
K
M
8 см
5. Теорема. (третий признак подобия треугольников: по трем сторонам) Если три стороны одного треугольника пропорциональны трем
сторонам другого треугольника , то такие треугольники подобные.АВ
ВС
АС
k
А1 В1 В1С1 А1С1
ΔАВС ~ Δ А1В1С1
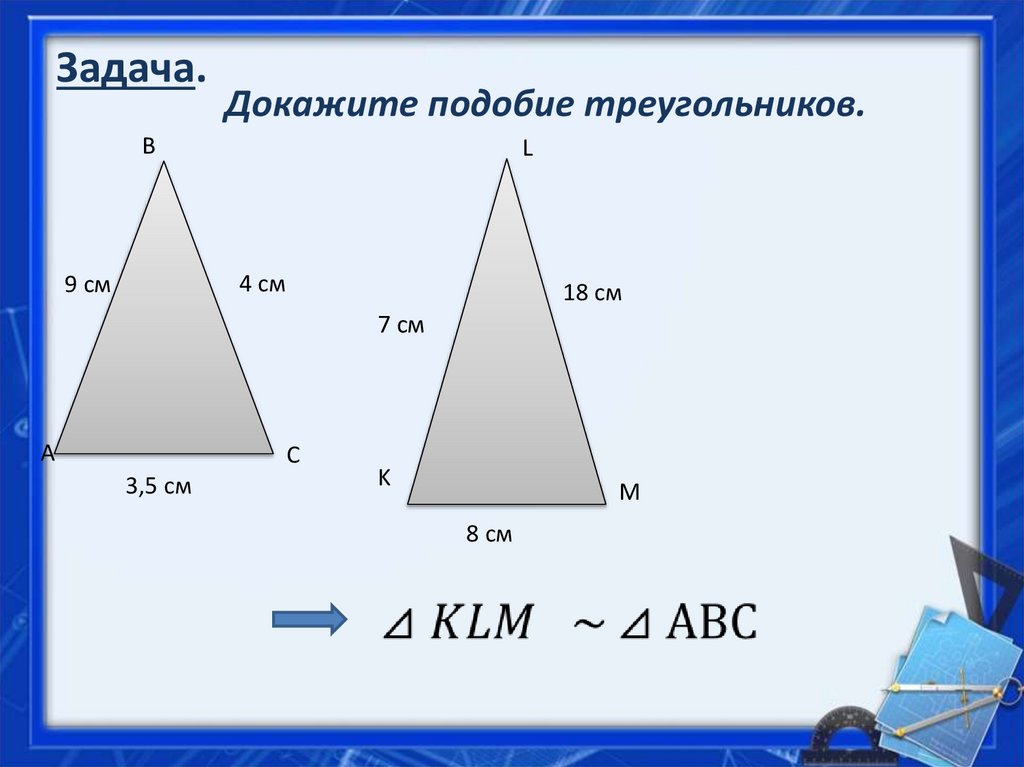
6. Задача.
Докажите подобие треугольников.В
L
4 см
9 см
18 см
7 см
А
С
3,5 см
K
M
8 см
7. Докажите, что отрезок, соединяющий основания двух высот остроугольного треугольника, отсекает от данного треугольника ему
Задача.Докажите, что отрезок, соединяющий основания двух
высот остроугольного треугольника, отсекает от
данного треугольника ему подобный.
Дано:
ΔАВС – остроугольный, АА1 ḻ ВС, СС1 ḻ АВ
Док-ть: ΔАВС ~ Δ А1ВС1
Доказательство:
ΔАВА1 и ΔСВС1 - прямоугольные, ʟВ – общий.
Следовательно , ΔАВА1 ~ΔСВС1 по первому признаку
подобия треугольников .
АВ ВА1
Отсюда
.
ВС ВС1
АВ ВС
Тогда
.
ВА1 ВС1
Следовательно, ΔАВС ~ Δ А1В1С1
(по второму признаку подобия треугольников).



 Математика
Математика








