Похожие презентации:
Физика. 1 семестр
1.
ФИЗИКАЛектор: Холин Кирилл Владимирович
2.
Физика и техникаНа основе новых физических законов создается новая техника, а новая
техника позволяет провести новые физические измерения и выявить
новые физические законы. То есть новая техника создает новую физику,
а новая физика – новую технику.
Примеры
company name
Открытие Майклом Фарадеем явления электромагнитной индукции
позволило
создать
передающие
и
приемные
радиостанции,
телевидение, радиолокацию, современные автомобили, самолеты,
ракеты и вычислительную технику.
Предсказание
Альбертом
Эйнштейном
возможности
получения
вынужденного излучения атомов и молекул привело к созданию
лазерной
техники,
нелинейной
оптики,
голографии,
лазерной
спектроскопии, управляемых химических реакций. Возникли новые
технические направления – сварка и резка металла лазерным лучом,
лазерное оружие и т.д.
3.
МеханикаМеханика - часть физики, которая изучает закономерности
механического движения и причины, вызывающие или
изменяющие это движение.
Механическое движение - это изменение с течением времени
взаимного расположения тел или их частей.
company name
Архимед (287–212г. до н.э.) – основатель механики.
Галилей (1564-1642г.), Ньютон
сформировали механику.
(1643-1727г.)
–
окончательно
4.
МеханикаРазделы механики
1.
Кинематика: Рассматривается движение идеализированных тел, без
рассмотрения причин движения.
2.
Динамика: Рассматриваются причины возникновения механического
движения.
3.
Статика: Рассматриваются условия равновесия механических
систем под действием приложенных к ним сил и моментов.
Простейшие физические модели:
company name
• материальная точка - тело, обладающее массой, размерами которого в
данной задаче можно пренебречь.
• абсолютно твердое тело - тело, которое ни при каких условиях не может
деформироваться и при всех условиях расстояние между двумя точками
(или точнее между двумя частицами) этого тела остается постоянным.
5.
КинематикаПоступательное движение - это движение, при котором любая прямая,
жестко связанная с движущимся телом, остается параллельной своему
первоначальному положению.
Вращательное движение - это движение, при котором все точки тела
движутся по окружностям, центры которых лежат на од-ной и той же
прямой, называемой осью вращения.
Любое движение твердого тела можно представить как комбинацию
поступательного и вращательного движений.
company name
Положение материальной точки определяется по отношению к какомулибо другому, произвольно выбранному телу, называемому телом
отсчета.
С телом отсчета связывается система отсчета - совокупность системы
координат и часов.
6.
Декартова система координатЧисло независимых величин,
полностью определяющих
положение точки в
пространстве, называется
числом степеней свободы.
Кинематические уравнения
движения материальной точки
company name
x=x(t) y=y(t) z=z(t)
7.
Траектория, путь, перемещениеТраектория — линия, описываемая в пространстве движущейся точкой.
Длина участка траектории, пройденного материальной точкой с момента
начала отсчета времени, называется длиной пути и является скалярной
функцией времени.
S S (t )
r
Вектор
проведенный из начального положения движущейся точки в
company name
положение ее в данный момент времени (приращение радиуса-вектора
точки
за
рассматриваемый
промежуток
времени),
называется
перемещением.
При прямолинейном движении вектор перемещения совпадает с
соответствующим участком траектории и модуль перемещения r равен
пройденному пути S .
8.
СкоростьДля характеристики движения материальной точки вводится векторная
величина - скорость, которой определяется как быстрота движения, так и
его направление в данный момент времени.
Вектор средней скорости:
company name
Вектор мгновенной скорости:
t t
Следовательно:
При равномерном движении:
и
s vdt
s v t
t
9.
УскорениеФизической величиной, характеризующей быстроту изменения скорости
по модулю и направлению, является ускорение.
Вектор среднего ускорения:
v
a
t
Вектор мгновенного ускорения:
При прямолинейном равнопеременном движении:
company name
, следовательно
10.
Ускорение при вращательном движенииТангенциальная составляющая ускорения:
Нормальная составляющая ускорения:
company name
Также называют центростремительным ускорением
Полное ускорение:
11.
Угловая скоростьМодуль вектора d равен углу поворота,
а его направление совпадает с
направлением
поступательного
движения
острия
винта,
головка
которого вращается в направлении
движения точки по окружности, т. е.
подчиняется правилу правого винта.
Угловой скоростью называется векторная величина,
первой производной угла поворота тела по времени.
2
откуда
T
определяемая
v R
company name
Период вращения (Т) - время, за которое точка совершает один полный
оборот, т. е. поворачивается на угол 2 .
Число полных оборотов, совершаемых телом при равномерном его
движении по окружности в единицу времени, называется частотой
вращения.
1
T
2
2
12.
Угловое ускорениеУгловым ускорением называется векторная величина, определяемая
первой производной угловой скорости по времени.
Зная, что v R
,
,
можно найти
company name
и
В случае равнопеременного движения точки по окружности:
13.
Динамика. Первый закон Ньютона.«Математические начала натуральной философии» (1687г.) Исаак Ньютон
Первый закон Ньютона (закон инерции): всякая материальная точка
(тело) сохраняет состояние покоя или равномерного прямолинейного
движения до тех пор, пока воздействие со стороны других тел не
заставит ее изменить это состояние.
company name
Первый закон Ньютона выполняется не во всякой системе отсчета, а те
системы, по отношению к которым он выполняется, называются
инерциальными системами отсчета.
Инерциальной системой отсчета является такая система отсчета,
относительно которой материальная точка, свободная от внешних
воздействий,
либо
покоится,
либо
движется
равномерно
и
прямолинейно.
14.
Второй закон Ньютона.Масса тела — физическая величина, являющаяся одной из основных
характеристик материи, определяющая ее инерционные (инертная масса)
и гравитационные (гравитационная масса) свойства.
Сила - это векторная величина, являющаяся мерой механического
воздействия на тело со стороны других тел или полей, в результате
которого тело приобретает ускорение или изменяет свою форму и
размеры.
Второй закон Ньютона (основной закон динамики поступательного
движения) - ускорение, приобретаемое материальной точкой (телом),
пропорционально вызывающей его силе, совпадает с ней по
направлению и обратно пропорционально массе материальной точки
(тела).
company name
или
dp
p mv F
dt
уравнение движения материальной точки
15.
Третий закон Ньютонаcompany name
Третий закон Ньютона: всякое действие материальных точек (тел) друг на
друга носит характер взаимодействия; силы, с которыми действуют друг
на друга материальные точки, всегда равны по модулю, противоположно
направлены и действуют вдоль прямой, соединяющей эти точки.
F12 - сила, действующая на первую материальную точку со стороны
второй;
F21 - сила, действующая на вторую материальную точку со стороны
первой.
Эти силы приложены к разным материальным точкам (телам), всегда
действуют парами и являются силами одной природы.
16.
Преобразования координат ГалилеяСистема К’ (с координатами х’, у’, z’), движется относительно системы К (с
координатами х, у, z) равномерно и прямолинейно со скоростью u
(u =
const). Скорость u направлена вдоль OO’.
К’
относительная скорость,
относительное ускорение
company name
К
абсолютная скорость,
абсолютное ускорение
или
17.
Принцип относительности ГалилеяИнвариантность означает независимость, неизменность относительно
каких-либо физических условий. В математике под инвариантностью
понимается
неизменность
величины
относительно
каких-либо
преобразований.
При переходе от одной инерциальной системы отсчета к другой не
меняется как само время, так и длительность какого-либо события (по
Галилею – инвариант!).
Теперь мы имеем право продифференцировать
координат Галилея по времени и получаем:
преобразования
Для ускорения получаем:
(тоже инвариант!)
company name
следовательно F F '
Принцип относительности Галилея: уравнения динамики при переходе от
одной инерциальной системы отсчета к другой формулируются
одинаково.
18.
Предпосылки к закону сохранения импульсаСовокупность материальных точек (тел), рассматриваемых как единое
целое, называется механической системой.
Силы взаимодействия между материальными точками механической
системы называются внутренними.
Силы, с которыми на материальные точки системы действуют внешние
тела, называются внешними.
company name
Механическая система тел, на которую не действуют внешние силы,
называется замкнутой (или изолированной).
Если мы имеем механическую систему, состоящую из многих тел, то,
согласно третьему закону Ньютона, силы, действующие между этими
телами, будут равны и противоположно направлены, т. е. геометрическая
сумма внутренних сил равна нулю!
19.
Закон сохранения импульсаЗапишем второй закон Ньютона для n тел механической системы:
равнодействующие внутренних сил
равнодействующие внешних сил
Складываем эти уравнения:
company name
Следовательно:
В случае отсутствия внешних сил:
Импульс замкнутой системы сохраняется, т. е. не изменяется с течением
времени.
20.
Фундаментальность закона сохранения импульсаcompany name
Закон сохранения импульса справедлив не только в классической
физике, он выполняется и для замкнутых систем микрочастиц (они
подчиняются законам квантовой механики). Это фундаментальный закон
природы, являющийся следствием определенного свойства симметрии
пространства — его однородности.
Однородность пространства заключается в том, что при параллельном
переносе в пространстве замкнутой системы тел как целого ее
физические свойства и законы движения не изменяются, иными словами,
не зависят от выбора положения начала координат инерциальной
системы отсчета.
21.
Центр инерцииЦентром масс (или центром инерции) системы материальных точек
называется воображаемая точка С, положение которой характеризует
распределение массы этой системы. Ее радиус-вектор равен:
аддитивность массы
Скорость центра масс:
company name
Следовательно:
Импульс системы равен произведению массы системы на скорость ее
центра масс.
22.
Закон сохранения центра инерцииМожно записать:
закон движения центра масс
company name
В случае отсутствия внешних сил:
Центр масс замкнутой системы либо
равномерно, либо остается неподвижным.
движется
прямолинейно
и
23.
Реактивное движениеУравнение движения тела переменной массы на примере
движения ракеты: если в момент времени t масса ракеты m, а ее
скорость v, то по истечении времени dt ее масса уменьшится на
dm и станет равной m - dm, a скорость станет равной v - dv.
dp m dm v dv dm v u mv
где u - скорость истечения газов относительно ракеты. Тогда:
dp mdv u dm
следовательно:
company name
или
Если F=0, то
или
реактивная сила
уравнение движения тела
переменной массы
формула Циолковского
24.
Энергия, работаЭнергия - универсальная мера различных форм движения и
взаимодействия. С различными формами движения материи связывают
различные формы энергии: механическую, тепловую, электромагнитную,
ядерную и другие.
Чтобы количественно характеризовать процесс обмена энергией между
взаимодействующими телами, в механике вводится понятие работы
силы.
Элементарной работой силы F на перемещении dr называется скалярная
величина:
company name
dA ( Fdr ) F cos ds FS ds
[Дж]
25.
МощностьРабота силы на участке траектории от точки 1 до точки 2 равна:
Чтобы охарактеризовать скорость совершения работы, вводят понятие
мощности:
company name
[Вт]
26.
Кинетическая энергияКинетическая энергия механической системы - энергия механического
движения этой системы.
Работа силы F на пути, который тело прошло за время возрастания
скорости от 0 до v, идет на увеличение кинетической энергии dT тела.
company name
dA dT
Кинетическая энергия зависит от выбора системы отсчета!
27.
Силовое полеФизическое поле - одна из форм материи, характеризующая все точки
пространства и времени, и поэтому обладающая бесконечным числом
степеней свободы (посредник, благодаря которому действие от одного
тела передается к другому на расстоянии) .
Потенциальное силовое поле – поле, в котором работа, совершаемая
действующими силами при перемещении тела из одного положения в
другое, не зависит от того, по какой траектории это перемещение
произошло, а зависит только от начального и конечного положений.
company name
Консервативные силы (потенциальные силы) – силы, работа которых не
зависит от формы траектории (зависит только от начальной и конечной
точки приложения сил)
Если работа, совершаемая силой, зависит от траектории перемещения
тела из одной точки в другую, то такая сила называется диссипативной.
28.
Потенциальная энергияТела, находясь в потенциальном поле сил, обладают потенциальной
энергией.
Потенциальная энергия - механическая энергия системы
определяемая их взаимным расположением и характером
взаимодействия между ними.
тел,
сил
Работа консервативных сил при элементарном (бесконечно малом)
изменении конфигурации системы равна приращению потенциальной
энергии, взятому со знаком «-» (работа совершается за счет убыли
потенциальной энергии)
company name
dA dП
29.
Потенциальная энергияИли в векторном виде:
где
company name
или
градиент скаляра П
оператор Гамильтона («набла»-оператор)
Конкретный вид функции П зависит от характера силового поля.
Например:
потенциальная энергия в поле Земли:
потенциальная энергия упругодеформированного тела:
30.
Полная энергияПолная механическая энергия системы - энергия механического
движения и взаимодействия, равна сумме кинетической и потенциальной
энергий.
company name
Полная механическая энергия системы равна сумме кинетической и
потенциальной энергий.
31.
Закон сохранения энергииЗапишем второй закон Ньютона для n тел механической системы:
равнодействующие внутренних
консервативных сил
равнодействующие внешних
консервативных сил
равнодействующие внешних
неконсервативных сил
Двигаясь под действием сил, материальные точки системы за интервал
времени dt совершают перемещения, соответственно равные
company name
Умножив каждое из уравнений скалярно на соответствующее
перемещение и сложив после этого уравнения получим:
32.
Закон сохранения энергииприращение кинетической
приращение
энергии
потенциальной энергии
работа внешних
неконсервативных сил
d (T П) dA
company name
если внешние неконсервативные силы отсутствуют, то
или
33.
Закон сохранения энергииЗакон сохранения энергии: в системе тел, между которыми действуют
только консервативные силы, полная механическая энергия сохраняется,
т. е. не изменяется со временем.
Механические
системы,
на
тела
которых
действуют
только
консервативные
силы
(внутренние
и
внешние),
называются
консервативными системами.
Закон сохранения энергии (версия 2): в консервативных системах полная
механическая энергия сохраняется.
company name
Существует еще один вид систем - диссипативные системы, в которых
механическая энергия постепенно уменьшается за счет преобразования в
другие (немеханические) формы энергии. Этот процесс получил название
диссипации (или рассеяния) энергии.
Закон сохранения механической энергии связан с однородностью
времени!
34.
Твердое тело в механике. Момент инерции.Моментом инерции системы (тела) относительно данной оси называется
физическая величина, равная сумме произведений масс п материальных
точек системы на квадраты их расстоянии до рассматриваемой оси:
company name
В случае непрерывного распределения масс:
Момент инерции тела относительно некоторой оси равен сумме моментов
инерции частей тела относительно той же оси (аддитивная величина).
35.
company nameТеорема Штейнера
Теорема Штейнера: момент инерции тела относительно произвольной
оси равен моменту его инерции относительно параллельной оси,
проходящей через центр масс тела, сложенному с произведением массы
тела на квадрат расстояния а между осями:
36.
Момент силы.Моментом силы относительно неподвижной точки О называется
физическая величина, определяемая векторным произведением радиусавектора, проведенного из точки О в точку приложения силы, на силу.
M rF
l - плечо силы
Модуль:
Моментом силы относительно неподвижной оси z называется скалярная
величина, равная проекции на эту ось вектора момента силы,
определенного относительно произвольной точки данной оси.
Работа на поворот тела:
dA F S sin F sin rd M z d
company name
Работа идет на увеличение кинетической энергии:
J 2
J d M z d
dA dT d
2
d
M z Jz
J z
dt
уравнение динамики вращательного движения твердого тела
относительно неподвижной оси
37.
Момент импульса.Моментом импульса (количества движения) материальной точки
относительно неподвижной точки О называется физическая величина,
определяемая векторным произведением:
L r p r , mv
Модуль:
l - плечо импульса
Моментом импульса относительно неподвижной оси называется
скалярная величина, равная проекции на эту ось вектора момента
импульса, определенного относительно произвольной точки данной оси.
n
n
n
Lz mi vi ri mi ri mi ri 2 J z
2
company name
i 1
i 1
i 1
Продифференцируем по времени:
уравнение динамики вращательного движения твердого тела
относительно неподвижной оси
38.
Закон сохранения момента импульса.Можно показать, что:
Если М=0, то:
закон сохранения момента импульса
company name
Закон сохранения момента импульса — фундаментальный закон
природы. Он связан со свойством симметрии пространства — его
изотропностью.
39.
company nameНебольшое отступление.
40.
Силы инерции.Системы отсчета, движущиеся относительно инерциальной системы с
ускорением, называются неинерциальными. Однако законы динамики
можно применять и для них, если ввести в рассмотрение так называемые
силы инерции.
ma F Fин Fц Fк
company name
Силы инерции при
ускоренном
поступательном
движении системы
отсчета
Силы инерции,
действующие на тело,
покоящееся во
вращающейся системе
отсчета.
(центробежная сила)
Силы инерции,
действующие на тело,
движущееся во
вращающейся системе
отсчета.
(сила кориолиса)
41.
Элементы релятивистской механики.Опыт Майкельсона – Морли (1881г., 1887г.) по обнаружению эфирного
ветра показал, что скорости света в двух движущихся относительно друг
друга системах равны.
company name
Выявлено противоречие между классической теорией и уравнениями
Максвелла.
В связи с этим А. Эйнштейном в 1905 г. была выдвинута специальная
теория относительности, которая часто называется также релятивистской
теорией, а специфические явления, описываемые этой теорией, релятивистскими эффектами.
42.
company nameПостулаты СТО.
I.
Принцип
относительности:
никакие
опыты
(механические,
электрические,
оптические),
проведенные
внутри
данной
инерциалыюй системы отсчета, не дают возможности обнаружить,
покоится ли эта система или движется равномерно и прямолинейно;
все законы природы инвариантны по отношению к переходу от одной
инерциальной системы отсчета к другой.
II.
Принцип инвариантности скорости света: скорость света в вакууме
не зависит от скорости движения источника света или наблюдателя и
одинакова во всех инерциальных системах отсчета.
43.
Преобразования Лоренца.Преобразования
Галилея
company name
следовательно
Отсчет времени имеет
относительный характер!
Время и пространство связаны.
Существует только пространство-время!
44.
Одновременность событий в разных системах отсчета.company name
Если события в системе К пространственно разобщены,
одновременны, то в системе К', согласно преобразованиям Лоренца:
но
Таким образом, в системе К' эти события, оставаясь пространственно
разобщенными, оказываются и неодновременными.
45.
Длительность событий в разных системах отсчета.company name
Длительность события, происходящего в некоторой точке, наименьшая в
той инерциальной системе отсчета, относительно которой эта точка
неподвижна.
Часы, движущиеся относительно инерциальной системы отсчета, идут
медленнее покоящихся часов.
46.
Длина тел в разных системах отсчета.Линейные размеры тела наибольшие в той инерциальной системе
отсчета, относительно которой тело покоится.
company name
Поперечные размеры тела не зависят от скорости его движения и
одинаковы во всех инерциальных системах отсчета.
Лоренцево сокращение длины тем больше, чем больше скорость
движения.
47.
Релятивистский закон сложения скоростей.Где v – скорость движения одной системы относительно другой
company name
Скорость света в вакууме
невозможно превысить.
есть
предельная
скорость,
которую
48.
ИнтервалОтносительный характер длин и промежутков времени в СТО означает
относительность отдельных компонентов какой-то реальной физической
величины, не зависящей от системы отсчета (инвариант). Этой величиной
является интервал.
company name
Можно показать, что:
Инвариантность интервала между двумя событиями свидетельствует о
том, что пространство и время связаны между собой и образуют единую
форму существования материи – «пространство-время».
49.
Уравнение движения релятивистской частицы.m0 - масса, измеренная в той инерциальной системе
относительно которой материальная точка находится в покое.
- релятивистский импульс материальной точки
company name
следовательно
Уравнение движения релятивисткой частицы
(основной закон релятивистской динамики)
отсчета,
50.
Работа. Энергия.dT dA Fdr , следовательно:
Интегрируя получим:
Обобщая, можно сказать что полная энергия:
Сюда не входит потенциальная
энергия во внешнем поле!
company name
закон взаимосвязи (пропорциональности) массы и энергии
: энергия покоя
: взаимосвязь полной энергии и импульса
51.
Молекулярная физика и термодинамикаМолекулярная физика и термодинамика — разделы физики, в которых
изучаются макроскопические процессы в телах, связанные с огромным
числом содержащихся в них атомов и молекул.
Существует 2 метода изучения:
company name
1. статистический метод (молекулярно-кинетический) - свойства
макроскопической системы в конечном счете определяются свойствами
частиц системы, особенностями их движения и усредненными
значениями динамических характеристик этих частиц (скорости, энергии
и т.д.)
Молекулярная физика - раздел физики, в котором изучаются строение и
свойства вещества исходя из молекулярно-кинетических представлений,
основывающихся на том, что все тела состоят из молекул, находящихся в
непрерывном хаотическом движении.
52.
Термодинамика2. Термодинамический метод не рассматривает микропроцессы.
Термодинамика - раздел физики, в котором изучаются общие свойства
макроскопических систем, находящихся в состоянии термодинамического
равновесия, и процессы перехода между этими состояниями.
company name
Термодинамическая система - совокупность макроскопических тел,
которые взаимодействуют и обмениваются энергией как между собой, так
и с другими телами (внешней средой).
Состояние системы задается термодинамическими параметрами
(параметрами состояния) - совокупностью физических величин,
характеризующих свойства термодинамической системы (температура,
давление, удельный объем).
53.
Основные понятияТемпература - физическая величина, характеризующая
термодинамического равновесия макроскопической системы.
2 основные температурные шкалы:
Международная практическая (оС).
состояние
термодинамическая
(К)
и
T(K) = 273,15 + t(оС)
company name
Удельный объем - объем единицы массы.
Любое изменение в термодинамической системе, связанное с
изменением хотя бы одного из ее термодинамических параметров,
называется термодинамическим процессом.
Макроскопическая система находится в термодинамическом равновесии,
если ее состояние с течением времени не меняется.
54.
Идеальный газ. Закон Бойля-Мариотта.Модель идеального газа:
1) Собственный объем молекул газа пренебрежимо мал по сравнению с
объемом сосуда.
2) Между молекулами газа отсутствуют силы взаимодействия.
3) Столкновения молекул газа между собой и со стенками сосуда
абсолютно упругие.
Закон Бойля - Мариотта
company name
Для данной массы газа при постоянной температуре произведение
давления газа на его объем есть величина постоянная.
изотерма
55.
Законы Гей-Люссака1. Объем данной массы газа при постоянном давлении изменяется
линейно с температурой.
изобара
company name
2. Давление данной массы газа при постоянном объеме изменяется
линейно с температурой.
изохора
56.
Закон Авогадро. Закон Дальтона.Количество вещества измеряется в молях.
В одном моле различных веществ содержится одно и то же число
молекул, называемое постоянной Авогадро:
Закон Авогадро: моли любых газов при одинаковых температуре и
давлении занимают одинаковые объемы.
company name
Закон Дальтона: давление смеси идеальных
парциальных давлений входящих в нее газов.
газов
равно
сумме
Парциальное давление - давление, которое производил бы газ, входящий
в состав газовой смеси, если бы он один занимал объем, равный объему
смеси при той же температуре.
57.
Уравнение Клайперона-МенделееваИз законов Бойля-Мариота и Гей-Люсака:
Получаем, что
company name
Можно обобщить:
Молярная газовая постоянная
уравнение состояния идеального газа (Клапейрона – Менделеева)
58.
Другие представления закона Клайперона-Менделееваследовательно
Постоянная Больцмана:
company name
следовательно
где
- концентрация молекул
- количество вещества
59.
Основное уравнение молекулярно-кинетической теории идеальных газовЧисло ударов молекул о стенку:
Каждая молекула передает импульс:
?
средняя квадратичная скорость!
company name
Учитывая, что:
получим:
Е - суммарная кинетическая энергия
поступательного движения всех
молекул газа.
следовательно:
Средняя Екин одной молекулы
60.
ТемператураТак как
, то
Для 1 моль газа m = M:
С другой стороны:
company name
Значит:
, откуда:
Термодинамическая температура является мерой средней кинетической
энергии поступательного движения молекул идеального газа.
61.
Распределение МаксвеллаФункция распределения молекул по скоростям:
или
закон распределения молекул
идеального газа по скоростям
company name
Скорость, при которой функция распределения молекул идеального газа
по скоростям максимальна, называется наиболее вероятной скоростью:
Средняя скорость молекулы:
и получаем:
62.
Распределение молекул по значениям кинетической энергииИсходя из распределения молекул по скоростям:
можно найти распределение молекул газа по значениям кинетической
энергии:
следовательно:
,
company name
или
63.
Барометрическая формула и распределение Больцмана, следовательно
Из уравнения Клайперона-Менделеева:
Подставив получим:
company name
Интегрируя:
, получаем
или, учитывая, что
:
64.
Внутренняя энергияВнутренняя энергия - энергия хаотического (теплового) движения
микрочастиц системы (молекул, атомов, электронов, ядер) и энергия
взаимодействия этих частиц.
Внутренняя энергия - однозначная функция термодинамического
состояния системы, т.е. при переходе системы из одного состояния в
другое изменение внутренней энергии определяется только разностью
значений внутренней энергии этих состояний и не зависит от пути
перехода.
Средняя энергия молекулы:
company name
где:
откуда
или
65.
Первое начало термодинамикиКоличество теплоты - энергия, переданная системе внешними телами
путем теплообмена.
Допустим, что некоторая система (газ, заключенный в цилиндр под
поршнем), обладая внутренней энергией U1 получила некоторое
количество теплоты Q и, перейдя в новое состояние, характеризующееся
внутренней энергией U2, совершила работу А над внешней средой, т. е.
против внешних сил. В соответствии с законом сохранения энергии:
company name
или
или в более корректной форме:
Первое начало термодинамики: теплота, сообщаемая системе,
расходуется на изменение ее внутренней энергии и на совершение ею
работы против внешних сил.
66.
РаботаЕсли газ, расширяясь, передвигает поршень на бесконечно малое
расстояние dl, то производит над ним работу:
company name
следовательно:
Графически можно изображать только равновесные
процессы
процессы,
состоящие
из
последовательности равновесных состояний. Они
протекают так, что изменение термодинамических
параметров за конечный промежуток времени
бесконечно мало.
67.
ТеплоемкостьУдельная теплоемкость вещества - величина, равная количеству теплоты,
необходимому для нагревания 1 кг вещества на 1 К.
company name
Молярная теплоемкость - величина, равная количеству
необходимому для нагревания 1 моль вещества на 1 К:
Видно, что:
теплоты,
68.
Теплоемкости при постоянном объеме и давленииРазличают теплоемкости при постоянном объеме и постоянном
давлении, если в процессе нагревания вещества его объем или давление
поддерживается постоянным!
Запишем выражение первого начала термодинамики для 1 моль газа:
Если газ нагревается при постоянном объеме:
company name
Если газ нагревается при постоянном давлении:
уравнение Майера
69.
Теплоемкость многоатомных газовкоэфициент Пуассона
company name
Мы получили, что молярные теплоемкости определяются лишь числом
степеней свободы и не зависят от температуры. Это утверждение
молекулярно-кинетической теории справедливо в довольно широком
интервале температур лишь для одноатомных газов. Уже у двухатомных
газов число степеней свободы, проявляющееся в теплоемкости, зависит
от температуры
При
низких
температурах
наблюдается только поступательное
движение молекул, при комнатных добавляется их вращение, а при
высоких - к этим двум видам
движения
добавляются
еще
колебания молекул.
70.
Адиабатный процессАдиабатным называется процесс, при котором отсутствует теплообмен
между системой и окружающей средой.
К адиабатным процессам можно отнести все быстропротекающие
процессы.
Первое начало термодинамики для такого процесса:
или:
company name
В то же время из ур. Клайперона-Менделеева:
Исключаем температуру:
Решая, получим:
уравнение Пуассона
71.
Адиабатный процессС помощью уравнения Клайперона-Менделеева
перейдем к другим переменным:
Вычислим работу, совершаемую
адиабатном процессе.
газом
в
company name
адиабата
Изохорный, изобарный, изотермический и адиабатный процессы имеют
общую особенность - они происходят при постоянной теплоемкости
(политропные процессы)
Показатель политропы
72.
Виды термодинамических процессовТермодинамический процесс называется обратимым, если он может
происходить как в прямом, так и в обратном направлении, причем если
такой процесс происходит сначала в прямом, а затем в обратном
направлении и система возвращается в исходное состояние, то в
окружающей среде и в этой системе не происходит никаких изменений.
Все процессы, не являющиеся обратимыми, называются необратимыми.
Любой обратимый процесс является равновесным.
company name
Обратимые процессы - это идеализация реальных процессов.
Круговым процессом (или циклом) называется процесс, при котором
система, пройдя через ряд состояний, возвращается в исходное.
73.
Прямые и обратные циклыЕсли за цикл совершается положительная
работа, то он называется прямым, а если
отрицательная, то обратным.
Прямой цикл используется в тепловых двигателях – периодически
действующих двигателях, совершающих работу за счет полученной извне
теплоты.
company name
Обратный цикл используется в холодильных машинах - периодически
действующих установках, в которых за счет работы внешних сил теплота
переносится к телу с более высокой температурой.
Термический коэффициент полезного действия для кругового процесса:
Q1
—
количество
теплоты,
полученное системой
Q2 — количество теплоты, отданное
системой.
74.
ЭнтропияПриведенное количество теплоты - отношение теплоты, полученной
телом в изотермическом процессе, к температуре теплоотдающего тела.
Теория показывает, что приведенное количество теплоты, сообщаемое
телу в любом обратимом круговом процессе:
company name
Следовательно
- дифференциал некоторой функции состояния.
Эта функция состояния называется энтропией.
75.
Энтропия в молекулярной физикеДля обратимых процессов:
справедливо для
замкнутых систем
Для необратимых процессов:
Следовательно:
Неравенство Клаузиуса: энтропия замкнутой системы может либо
возрастать (в случае необратимых процессов), либо оставаться
постоянной (в случае обратимых процессов).
company name
Т.к. для адиабатного процесса
изоэнтропийным процессом.
и
, то его называют
Аддитивность энтропии: энтропия системы равна сумме энтропий тел,
входящих в систему.
76.
Энтропия в термодинамикеТермодинамическая вероятность состояния системы (W) - это число
способов, которыми может быть реализовано данное состояние
макроскопической
системы,
или
число
микросостояний,
осуществляющих данное макросостояние.
энтропия системы и термодинамическая вероятность связаны:
формула Больцмана
company name
Т.е. энтропия является мерой неупорядоченности системы! Чем больше
число микросостояний, реализующих данное макросостояние, тем
больше энтропия.
Согласно неравенству Клаузиуса процессы в замкнутой системе идут в
направлении увеличения числа микросостояний, от менее вероятных
состояний к более вероятным - до тех пор, пока вероятность состояния
не станет максимальной.
77.
Второе и третье начала термодинамикиВторое начало термодинамики
1-я формулировка: любой необратимый процесс в замкнутой системе
происходит так, что энтропия системы при этом возрастает.
2-я формулировка: в процессах, происходящих в замкнутой системе,
энтропия не убывает.
3-я формулировка: невозможен круговой прогресс, единственным
результатом которого является превращение теплоты, полученной от
нагревателя, в эквивалентную ей работу.
4-я формулировка: невозможен круговой процесс, единственным
результатом которого является передача теплоты от менее нагретого тела
к более нагретому.
company name
Третье начало термодинамики (теорема Нернста-Планка)
Энтропия всех тел в состоянии равновесия стремится к нулю по мере
приближения температуры к нулю кельвин.
78.
Цикл КарноТеорема Карно: Из всех периодически действующих тепловых машин,
имеющих одинаковые температуры нагревателей (Т1) и холодильников
(Т2), наибольшим КПД обладают обратимые машины; при этом КПД
обратимых машин, работающих при одинаковых температурах
нагревателей (Т1) и холодильников (T2), равны друг другу и не зависят от
природы рабочего тела (тела, совершающего круговой процесс и
обменивающегося энергией с другими телами), а определяются только
температурами нагревателя и холодильника.
company name
Цикл Карно - цикл, состоящий из четырех
последовательных обратимых процессов:
изотермического расширения, адиабатного
расширения,
изотермического
сжатия
и
адиабатного сжатия.
79.
Физическая кинетикаМежду двумя последовательными столкновениями молекулы проходят
некоторый путь, который называется длиной свободного пробега (l).
Но можно говорить только о средней длине свободного пробега молекул
(<l>).
- среднее число столкновений, испытываемых одной молекулой газа
за 1 с.
Минимальное расстояние, на которое сближаются при столкновении
центры двух молекул- эффективный диаметр молекулы (эффективное
сечение рассеяния) (d).
company name
Можно посчитать, что:
Следовательно:
80.
Явления переносаВ термодинамически неравновесных системах возникают особые
необратимые процессы, называемые явлениями переноса, в результате
которых происходит пространственный перенос энергии, массы,
импульса.
К явлениям переноса относятся:
Теплопроводность - обусловлена переносом энергии.
company name
Диффузия - обусловлена переносом массы.
Внутреннее трение - обусловлено переносом импульса.
81.
ТеплопроводностьЕсли в одной области газа средняя кинетическая энергия молекул
больше, чем в другой, то с течением времени вследствие постоянных
столкновений молекул происходит процесс выравнивания средних
кинетических энергий молекул, т.е., иными словами, выравнивание
температур.
Закон Фурье:
company name
- плотность теплового потока - величина, определяемая энергией,
переносимой в форме теплоты в единицу времени через единичную
площадку, перпендикулярную оси x.
- теплопроводность
- градиент температуры
82.
ДиффузияЯвление
диффузии
заключается
в
том,
что
происходит
самопроизвольное проникновение и перемешивание частиц двух
соприкасающихся газов, жидкостей и даже твердых тел; диффузия
сводится к обмену масс частиц этих тел, возникает и продолжается, пока
существует градиент плотности.
Закон Фика (для химически однородного газа):
company name
- плотность потока массы - величина, определяемая массой вещества,
диффундирующего в единицу времени через единичную площадку,
перпендикулярную оси х.
- диффузия (коэффициент диффузии).
- градиент плотности
83.
Внутреннее трениеМеханизм возникновения внутреннего трения между параллельными
слоями газа (жидкости), движущимися с различными скоростями,
заключается в том, что из-за хаотического теплового движения
происходит обмен молекулами между слоями, в результате чего импульс
слоя, движущегося быстрее, уменьшается, движущегося медленнее увеличивается, что приводит к торможению слоя, движущегося быстрее,
и ускорению слоя, движущегося медленнее.
Закон Ньютона
company name
или
- плотность потока импульса - величина, определяемая полным
импульсом, переносимым в единицу времени в положительном
направлении оси х через единичную площадку, перпендикулярную оси х.
- динамическая вязкость
- градиент скорости
84.
Фаза веществаФазой называется термодинамически равновесное состояние вещества,
отличающееся по физическим свойствам от других возможных
равновесных состояний того же вещества.
В пределах одного агрегатного состояния вещество может находиться в
нескольких фазах, отличающихся по своим свойствам, составу и
строению.
Переход вещества из одной фазы в другую - фазовый переход – всегда
связан с качественными изменениями свойств вещества.
company name
Фазовый переход 1 рода (плавление, кристаллизация) сопровождается
поглощением или выделением теплоты, называемой теплотой фазового
перехода. Характеризуются постоянством температуры, изменениями
энтропии и объема.
Фазовые переходы, не связанные с поглощением или выделением
теплоты и изменением объема, называются фазовыми переходам II рода.
Характеризуются постоянством объема и энтропии, но скачкообразным
изменением теплоемкости.
85.
Диаграмма состоянияЕсли система является однокомпонентной, то понятие фазы совпадает с
понятием агрегатного состояния.
Для наглядного изображения
диаграмма состояния.
фазовых
превращений
используется
Кривые на диаграмме называются кривыми
фазового равновесия, каждая точка на них
соответствует условиям равновесия двух
сосуществующих фаз: КП - твердого тела и
жидкости, КИ - жидкости и газа, КС твердого тела и газа.
company name
Уравнение Клайперона - Клаузиуса
L - теплота фазового перехода
Точка, в которой пересекаются эти кривые и которая, следовательно,
определяет условия одновременного равновесного сосуществования
трех фаз вещества, называется тройной точкой.
86.
Уравнение состояния реального газа1. Учет собственного объема молекул.
Фактический свободный объем, в котором могут двигаться молекулы
реального газа, не Vm, a Vm - b, где b — объем, занимаемый самими
молекулами. Объем b равен учетверенному собственному объему
молекул.
2. Учет притяжения молекул.
Действие сил притяжения газа приводит к появлению дополнительного
давления на газ, называемого внутренним давлением.
company name
Уравнение Ван-дер-Ваальса:
или:
87.
Изотермы Ван-дер-ВаальсаДля исследования поведения реального газа
рассмотрим
изотермы
Ван-дер-Ваальса
кривые зависимости р от Vm при заданных Т,
определяемые уравнением Ван-дер-Ваальса.
При высоких температурах изотерма реального
газа отличается от изотермы идеального газа
только некоторым искажением ее формы,
оставаясь монотонно спадающей кривой.
При некоторой температуре на изотерме имеется
лишь одна точка перегиба К. Эта изотерма
называется критической.
company name
Состояние с критическими параметрами (рк, VK,
TK) называется критическим состоянием.
Вещество в газообразном состоянии при
температуре ниже критической называется
паром, а пар, находящийся в равновесии со
своей жидкостью, называется насыщенным.
88.
Кристаллы. Монокристаллы.Поликристаллы.Твердые тела (кристаллы) характеризуются наличием значительных сил
межмолекулярного взаимодействия и сохраняют постоянными не только
свой объем, но и форму.
company name
Структура, для которой характерно регулярное расположение частиц с
периодической повторяемостью в трех измерениях, называется
кристаллической решеткой.
Точки, в которых расположены частицы, а точнее - средние равновесные
положения, около которых частицы совершают колебания, называются
узлами кристаллической решетки.
89.
Кристаллы. Монокристаллы.Поликристаллы.Монокристаллы - твердые тела, частицы которых образуют единую
кристаллическую решетку.
Закон постоянства углов (М.В. Ломоносов) - внешняя форма
монокристаллов одного типа может быть различной, но углы между
соответствующими гранями у них остаются постоянными.
company name
Характерной особенностью монокристаллов является их анизотропность,
т.е. зависимость физических свойств - упругих, механических, тепловых,
электрических, магнитных, оптических - от направления.
Поликристаллы - состоят из множества беспорядочно ориентированных
мелких кристаллических зерен.
90.
Кристаллографический признак кристалловСуществует два признака для классификации кристаллов:
1) Кристаллографический
2) Физический
Кристаллографический признак кристаллов
Важна только пространственная периодичность в расположении частиц,
поэтому можно отвлечься от их внутренней структуры, рассматривая
частицы как геометрические точки.
Симметрия кристаллической решетки - ее свойство совмещаться с собой
при
некоторых
пространственных
перемещениях,
например
параллельных переносах, поворотах, отражениях или их комбинациях и
т.д.
company name
Всякая пространственная решетка (решетка Браве) может быть
составлена повторением в трех различных направлениях одного и того
же структурного элемента - элементарной ячейки.
Существует 7 видов (сингоний) решеток Браве: триклинная, моноклинная,
ромбическая,
тетрагональная,
кубическая,
тригональная
и
гексагональная.
91.
Физический признак кристалловФизический признак кристаллов.
В зависимости от рода частиц, расположенных в узлах кристаллической
решетки, и характера сил взаимодействия между ними кристаллы
разделяются на четыре типа:
1. Ионные кристаллы. В узлах кристаллической решетки располагаются
поочередно ионы противоположного знака (NaCl, CsCl, KBr, MgO, CaO).
company name
Связь, обусловленная кулоновскими
разноименно
заряженными
ионами,
гетерополярной)
силами притяжения между
называется
ионной
(или
2. Атомные кристаллы. В узлах кристаллической решетки располагаются
нейтральные атомы, удерживающиеся в узлах решетки гомеополярными,
или ковалентными, связями квантово-механического происхождения
(алмаз, графит, германий, кремний).
92.
Физический признак кристаллов3. Металлические кристаллы. В узлах кристаллической решетки
располагаются положительные ионы металла (Li, Na, К, Rb, Cs, Сu, Ag, Pt,
Аu).
При образовании кристаллической решетки валентные электроны
отделяются от атомов и коллективизируются: они уже принадлежат не
одному атому, как в случае ионной связи, и не паре соседних атомов, как
в случае гомеополярной связи, а всему кристаллу в целом.
company name
4. Молекулярные кристаллы. В узлах кристаллической решетки
располагаются нейтральные молекулы вещества, силы взаимодействия
между
которыми
(ван-дер-ваальсовы
силы)
обусловлены
незначительным взаимным смещением электронов в электронных
оболочках атомов (парафин, спирт, резина, лед).
В некоторых твердых телах одновременно может осуществляться
несколько видов связи (графит)!
93.
Теплоемкость кристалловРассмотрим кристаллическую решетку, в узлах которой частицы (атомы,
ионы, молекулы), принимаемые за материальные точки, колеблются
около своих положений равновесия - узлов решетки - в трех взаимно
перпендикулярных направлениях.
Каждой составляющей кристаллическую решетку частице приписывается
три колебательных степени свободы, каждая из которых обладает
энергией кТ, тогда:
company name
и
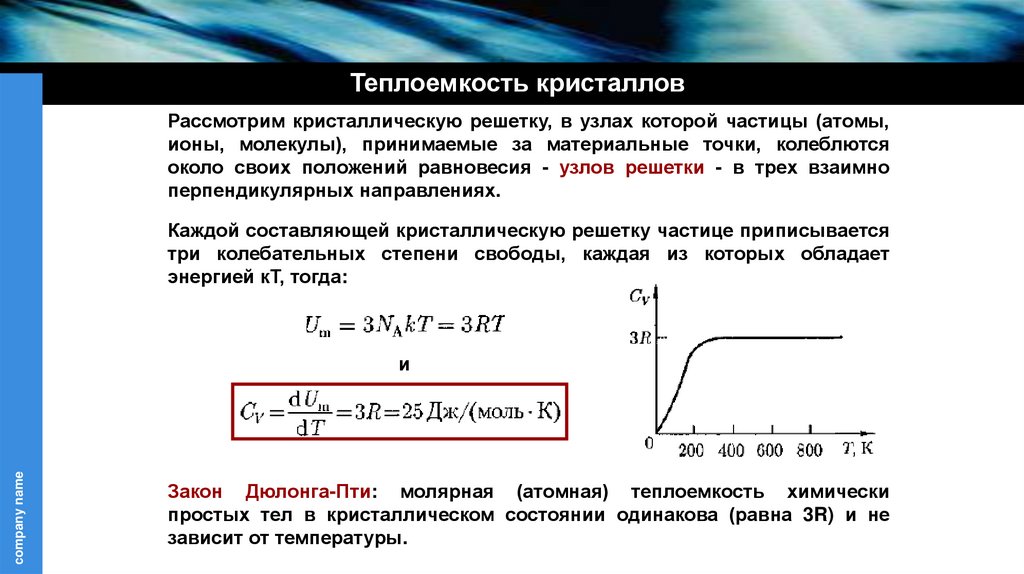
Закон Дюлонга-Пти: молярная (атомная) теплоемкость химически
простых тел в кристаллическом состоянии одинакова (равна 3R) и не
зависит от температуры.




























































































 Физика
Физика Механика
Механика








