Скалярное произведение векторов

1.

2.

11
12
Угол между векторами
1
10 А
2
В
a
9
b
a
b
a b= a
3
О
Лучи ОА и ОВ образуют угол АОВ.
Градусную меру этого угла
обозначим буквой a
8
a
4
7
5
Угол между векторами
равен a
6
aи b

3.

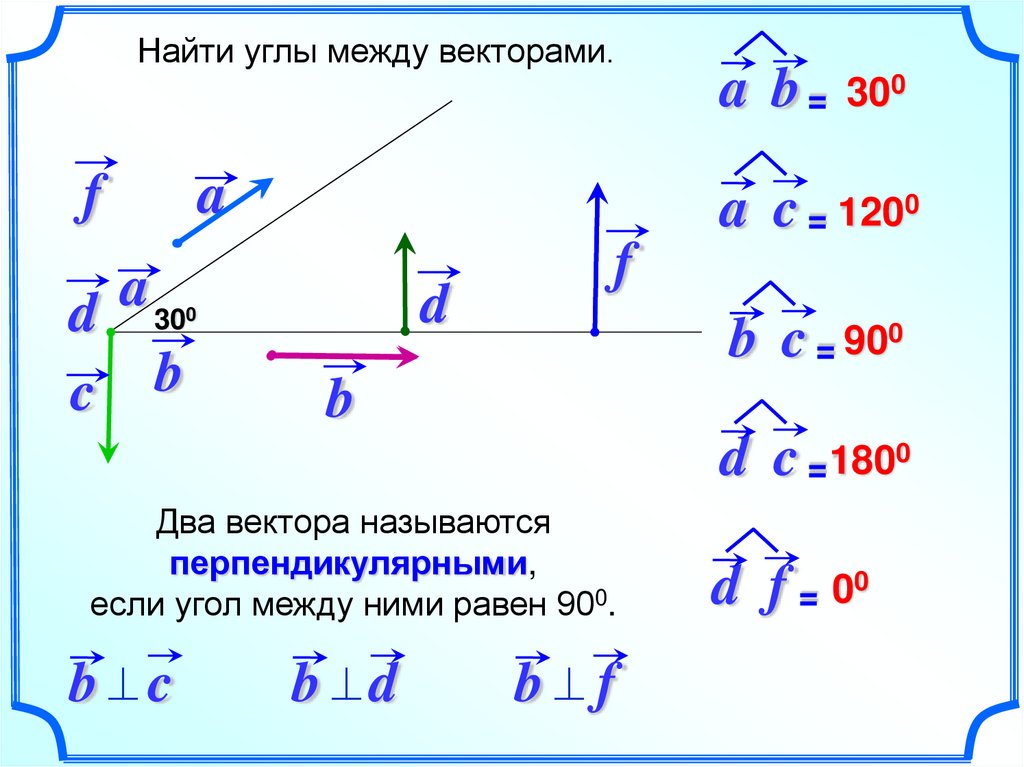
Найти углы между векторами.
f
a
a
d 30
c
b
a b = 300
a c = 1200
d
0
f
b c = 900
b
d c = 1800
Два вектора называются
перпендикулярными,
если угол между ними равен 900.
b^c
b ^d
b^f
d f = 00

4.

№ 1039 Диагонали квадрата пересекаются в точке О.
Найдите углы между векторами.
0
АВ, АС = 45
С
В
0
АВ, DА = 90
OА, OB = 900
О
OА, OС = 180
А
0
D
АC, BD = 90
0
АD, DB = 135
АO, OC = 0
0
0

5.

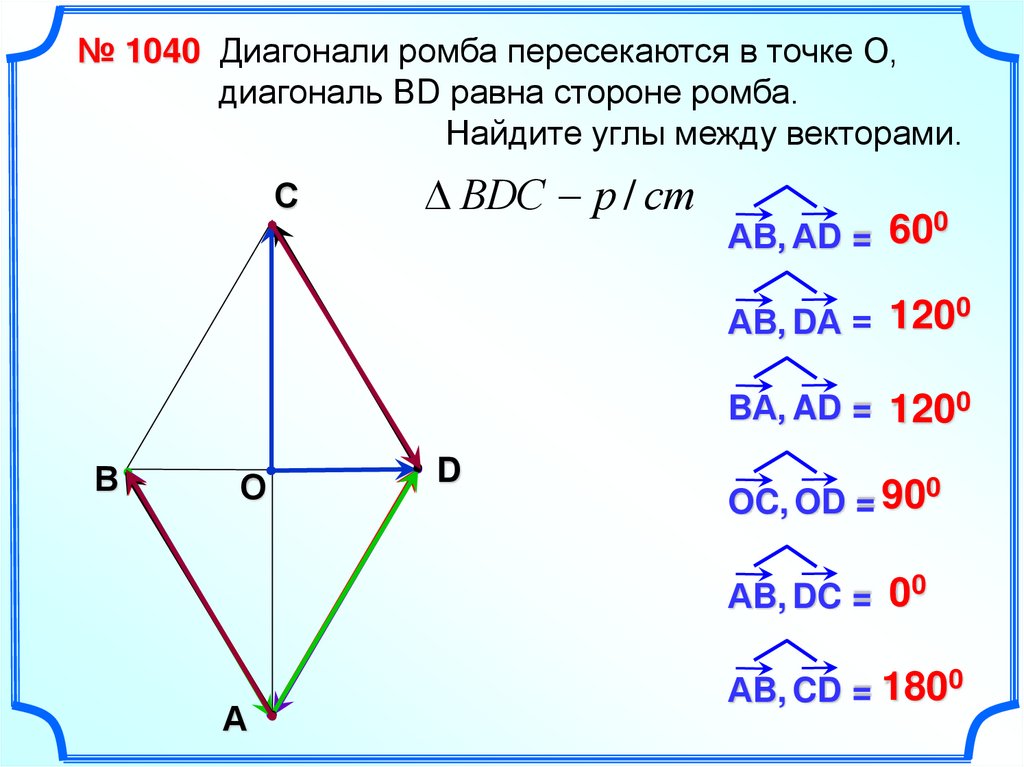
№ 1040 Диагонали ромба пересекаются в точке О,
диагональ ВD равна стороне ромба.
Найдите углы между векторами.
С
ВDC р / ст
АВ, АD = 60
0
АВ, DА = 120
0
BА, AD = 1200
В
О
D
OC, OD = 90
0
АB, DC = 00
А
АB, CD = 1800

6.

Сумма векторов – вектор.
Разность векторов – вектор.
Произведение вектора на число – вектор.
Скалярное произведение векторов – число.
Скалярным произведением двух векторов
называется произведение их длин на косинус
угла между ними.
a b = a b cos(a b )

7.

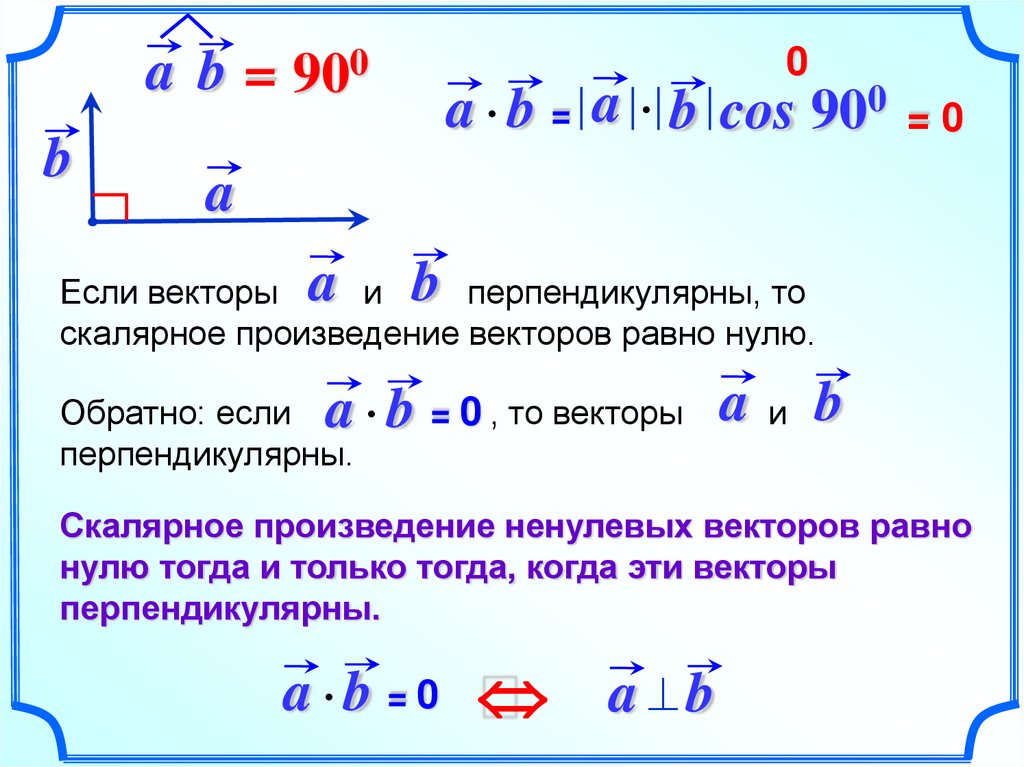
0
a b = 900
b
a b = a b cos 900 = 0
a
a
b
Если векторы
и
перпендикулярны, то
скалярное произведение векторов равно нулю.
a b = 0 , то векторы a и b
Обратно: если
перпендикулярны.
Скалярное произведение ненулевых векторов равно
нулю тогда и только тогда, когда эти векторы
перпендикулярны.
a b =0
a ^b

8.

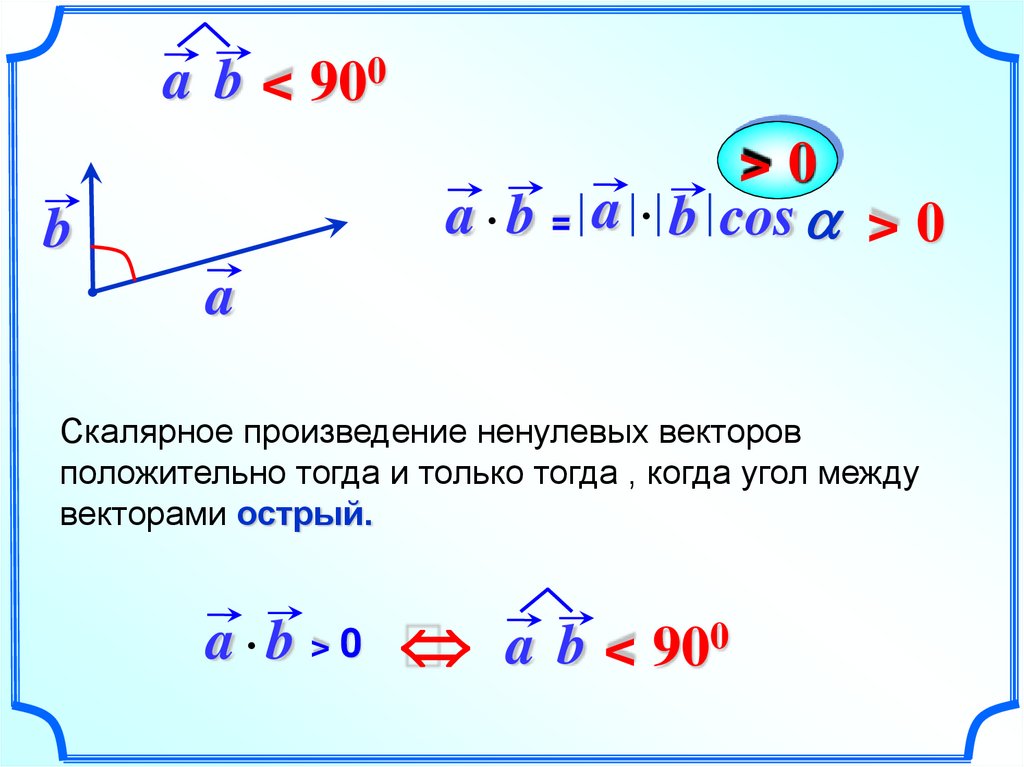
a b < 900
>0
a b = a b cos a > 0
b
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900

9.

a b > 900
<0
a b = a b cos a < 0
b
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900

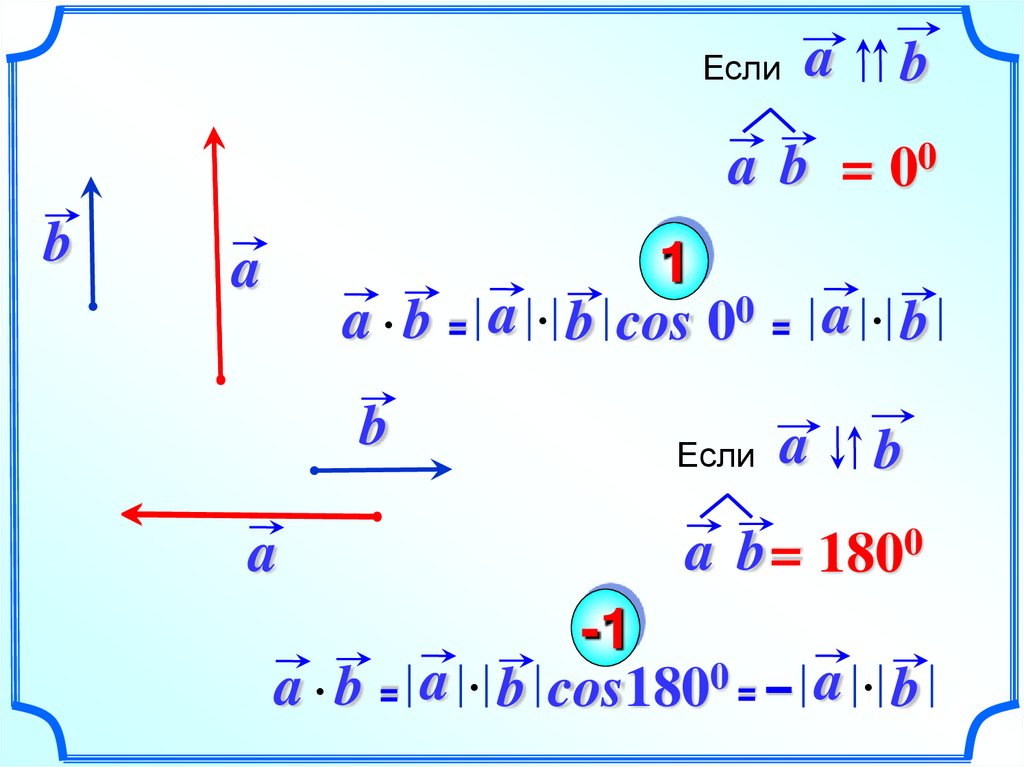
10.

Если
a
b
a b = 00
b
1
a b = a b cos 00 = a b
a
b
a
Если
a
b
a b = 1800
-1
a b = a b cos1800 = – a b

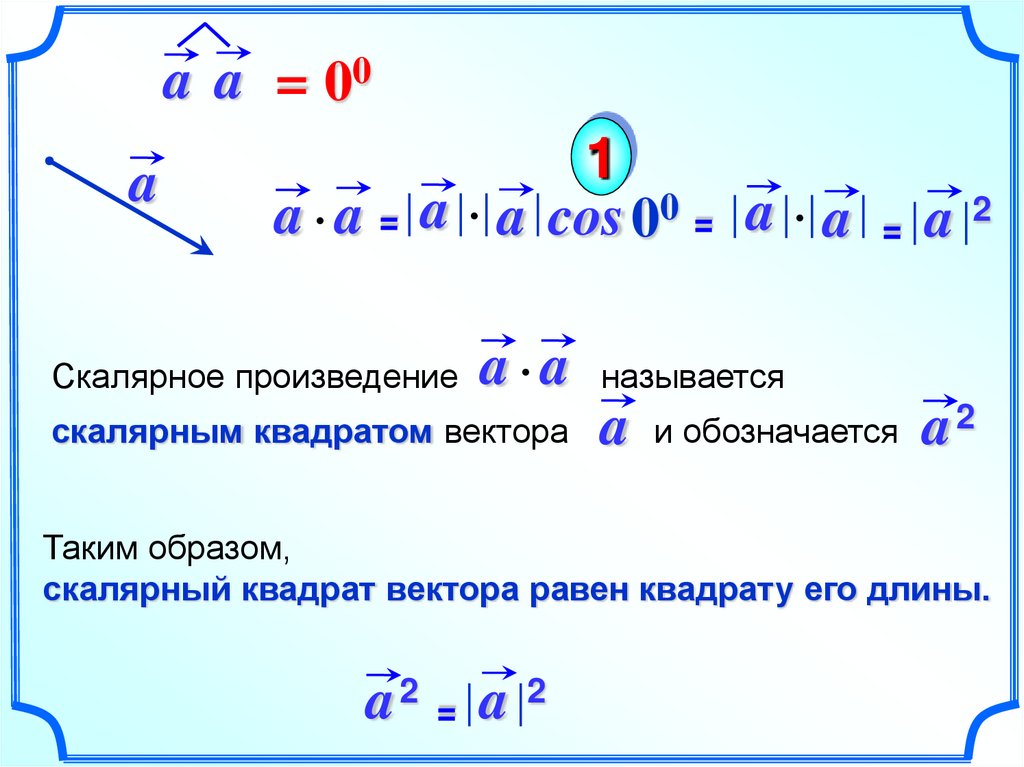
11.

a a = 00
a
1
a a = a a cos 00 = a a = a 2
a a называется
скалярным квадратом вектора a и обозначается a 2
Скалярное произведение
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
a2 = a 2

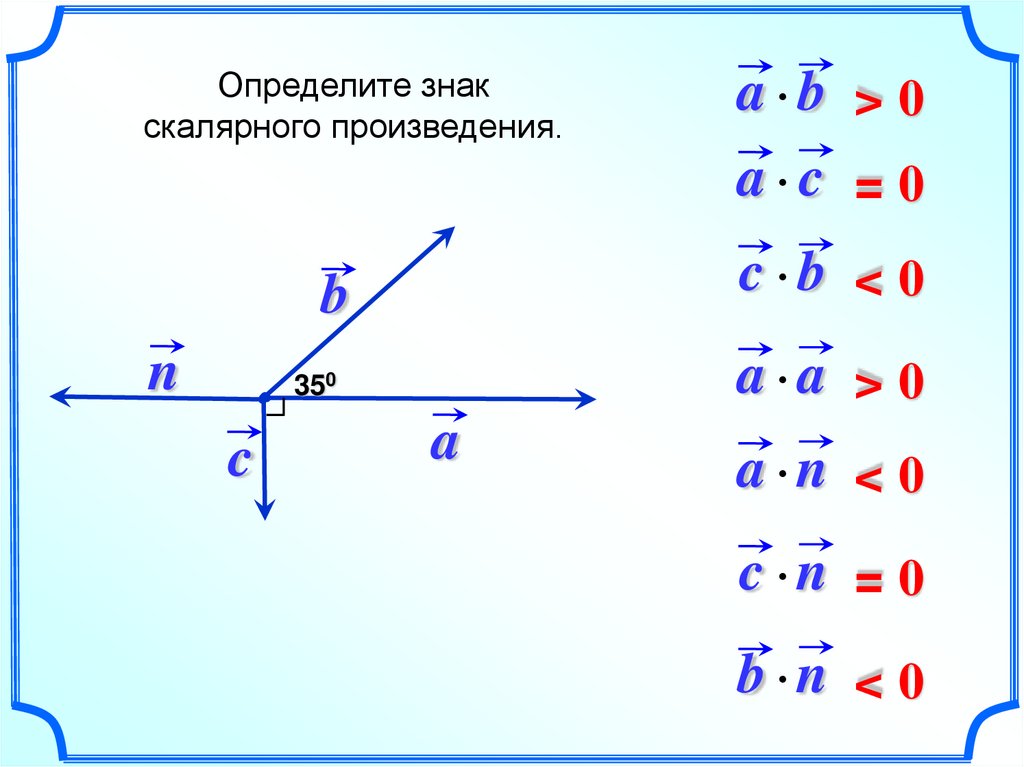
12.

Определите знак
скалярного произведения.
a a > 0
350
c
a c = 0
c b < 0
b
n
a b > 0
a
a n < 0
c n = 0
b n < 0

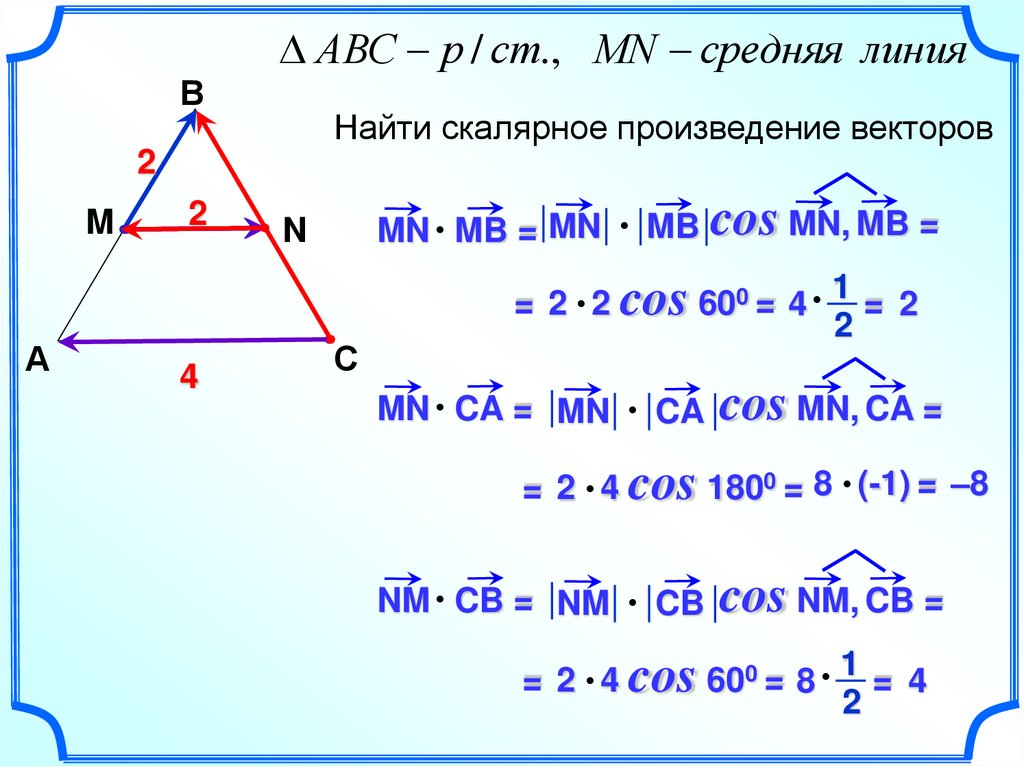
13.

АВC р / ст., МN средняя линия
В
Найти скалярное произведение векторов
2
M
2
MB cos MN, MB =
= 2 2 cos 60 = 4 1 = 2
2
MN MB = MN
N
0
А
4
С
CA cos MN, CA =
= 2 4 cos 180 = 8 (-1) = –8
MN CA = MN
0
CB cos NM, CB =
= 2 4 cos 60 = 8 1 = 4
2
NM CB = NM
0

14.

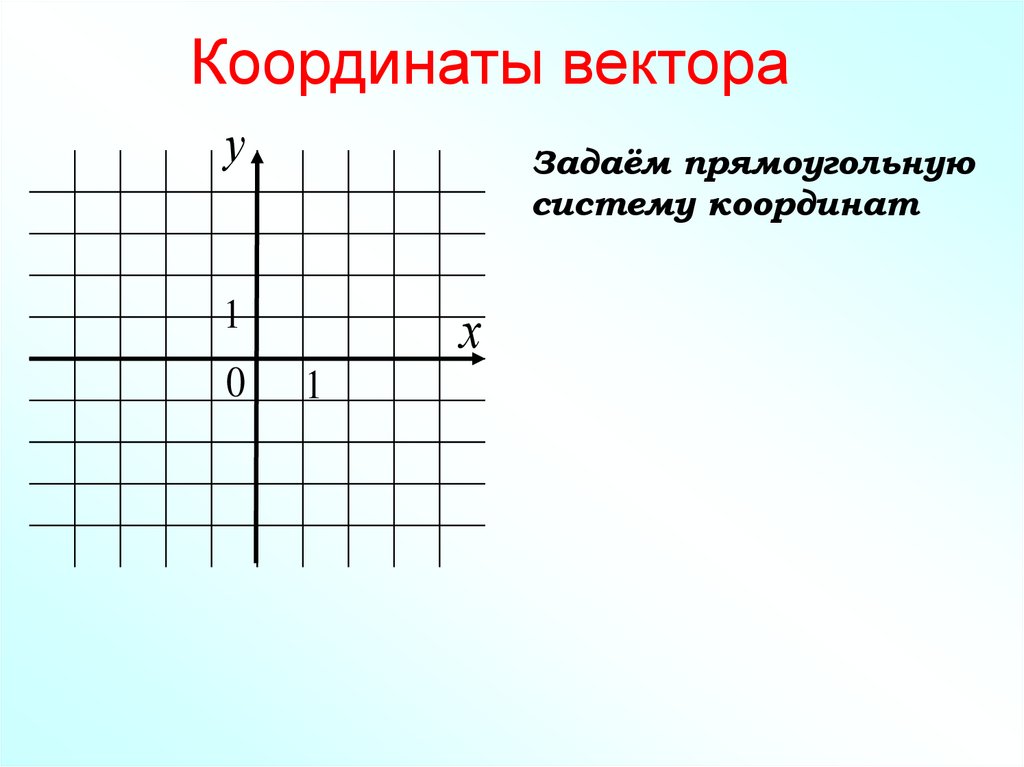
Координаты вектора
у
Задаём прямоугольную
систему координат
1
0
х
1

15.

Координаты вектора
у
1
j 1
0 i
Задаём единичные векторы
i и j - единичные
х
координатные
векторы
Задаём координаты
единичных векторов
i 1; 0 - вектор i
имеет координаты
1и0
j 0;1
- вектор j
имеет координаты
0и1

16.

17.

Координаты вектора
у
m
3
j
х
3 2 0 t
3
i
n
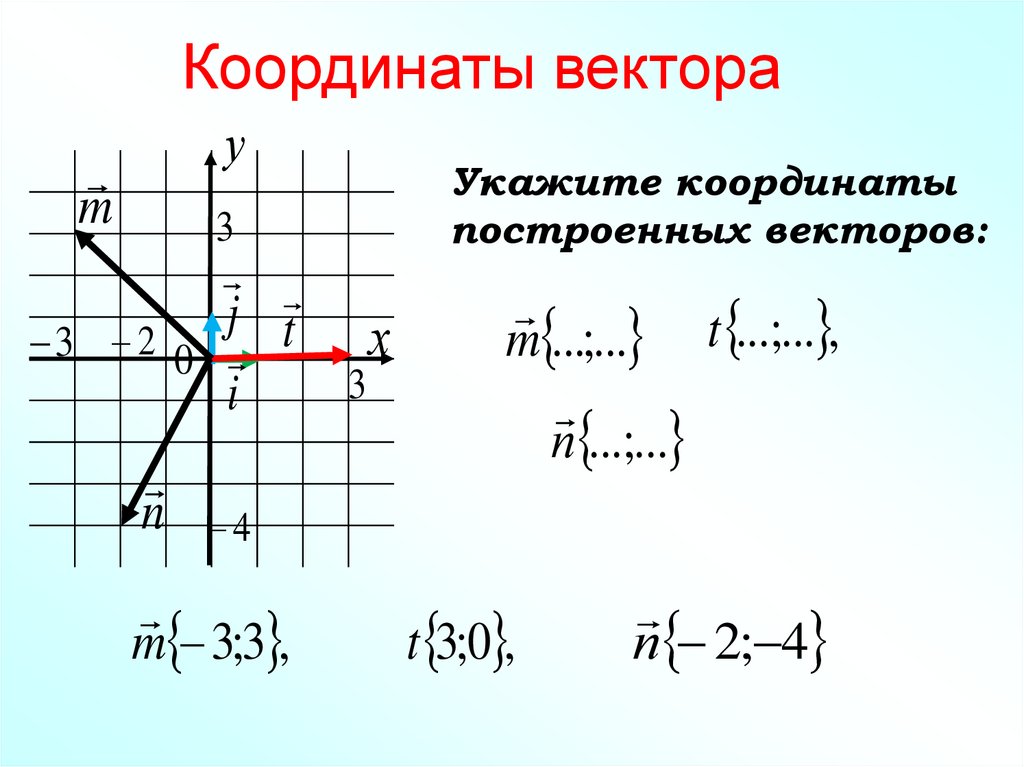
Укажите координаты
построенных векторов:
m ...;... t ...;... ,
п ...;...
4
m 3;3 ,
t 3;0 ,
п 2; 4

18.

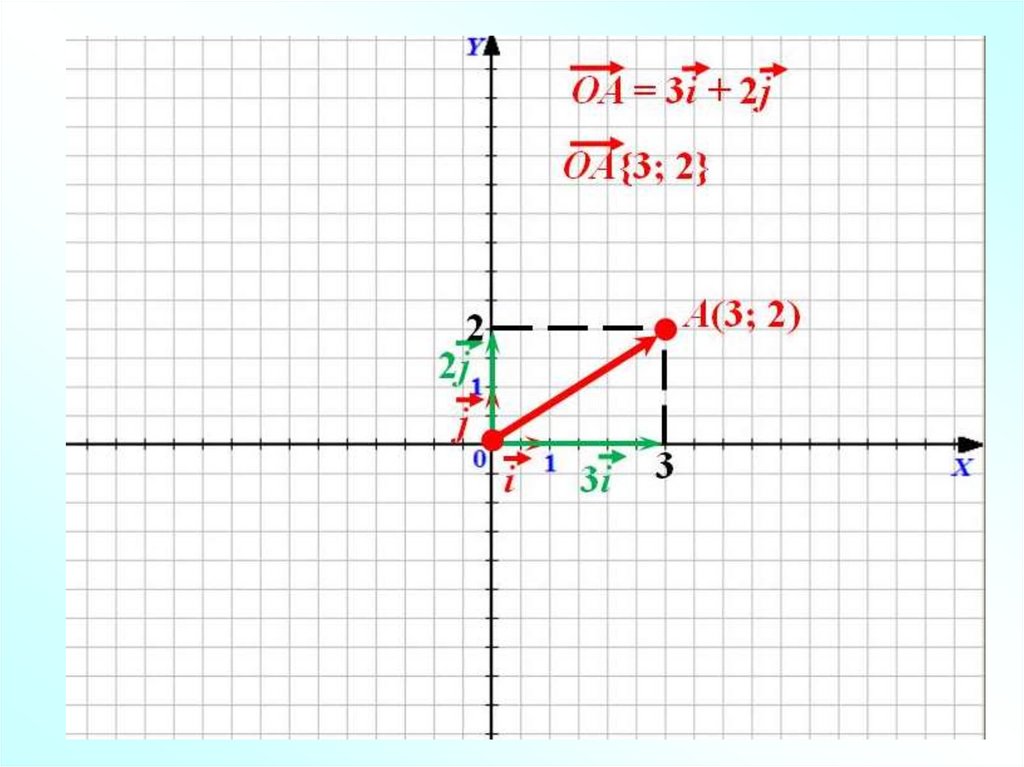
Назовите координаты векторов:
a 2i 3 j
1
b i 2j
2
c 8i
d i j
e 2 j
f i
a
b
c
d
e
f
a 2;3
1
b ; 2
2
c 8;0
d 1; 1
e 0; 2
f 1;0

19. Скалярное произведение в координатах

• Скалярным произведением двух
векторов на плоскости или в
трехмерном пространстве в
прямоугольной системе координат
называется сумма произведений
соответствующих координат векторов
⃗a и ⃗b .

20. Работа на уроке:

• №1047(а)
• №1048

21.

ДОМАШНЕЕ ЗАДАНИЕ:
выучить формулы, правила из презентации,
решить № 1047 (б,в)